SKS V/1 Informationsaustauschgerät mit Chiffrator; BArch
*48,
*128,
*219
COBEPШEHHO CEKPETHO
Geheime Verschlußsache
MfS 020/747/73
05. Ausfertigung 163 Blatt
Kryptologische Analyse des Chiffrators
des Systems OPERATION
Bestätigt: Leiter des Zentralen Chiffrierorgans
im Ministerium für Staatssicherheit
der Deutschen Demokratischen Republik
Schürrmann
Oberst
INHALT
Einleitung
Kapitel I Chiffrierverbindungen im System OPERATION
§1 Schema der Chiffrierverbindungen
§2 Nachrichten auf dem Übertragungskanal
1. Struktur der Nachrichten
2. Klartexteigenschaften
3. Nachrichtenübertragung
4. Informationsdichte
5. Blendnachrichten
6. Geheimhaltung der Nachrichten
Kapitel II Das Chiffriersystem im System OPERATION
§1 Forderungen an das Chiffriersystem
§2 Konzeption des Chiffriersystems
1. Chiffrierprinzip
2. Synchronisationsprinzip
3. Erzeugung der Additionsreihen
§3 Die Funktionen der Chiffriereinrichtung
1. Schlüsseleingabeeinheit
2. Synchronisationseinheit
3. Chiffrator und Prüf-Chiffrator
4. Steuerung
§4 Die Funktionseinheit einer Dechiffrier-
einrichtung
1. Schlüsseleingabeeinheit
2. Synchronisationseinheit
3. Dechiffrator
4. Steuerung
Kapitel III Die kryptologische Schaltung des Chiffrators
im System OPERATION
§1 Beschreibung der kryptologischen Schaltung
des Chiffrators
1. Kryptologische Schaltung
2.Beschreibung der Erzeugung eines Abschnittes
(wi)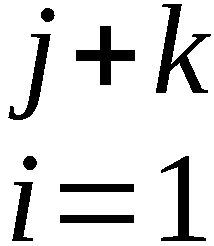 (k > 76) von W = (wi)
(k > 76) von W = (wi) ,
dessen Anfangsabschnitt (wi)
,
dessen Anfangsabschnitt (wi) als Additionsreihe genutzt wird.
3. Prüfung und Blockierung
§2 Das Schlüsselsystem
1. Kurzzeitschlüssel
2. Langzeitschlüssel
3. Reserveschlüssel
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der
kryptologischen Schaltung
2. Festlegung des Schlüsselsystems
3. Grundprinzip der Erzeugung der Folge W
4. Festlegung der Grundstruktur der krypto-
logischen Schaltung II
5. Festlegung der Parameter der kryptolo-
gischen Schaltung II
5.1 Anzahl der internen Arbeitstakte T 350 kHz
pro Übertragungstakt TÜi
5.2 Kurzzeitschlüssel
5.3 Zustandsspeicher U
5.4 Realisierung der Überführungsfunktion
5.5 Verarbeitung von FUi, S1 und S2
5.6 Einstellung des Anfangszustandes U(0)
5.7 Abgriff der Elemente wi von W
§4 Kryptologische Sicherheit im System OPERATION
§5 Änderungsmöglichkeiten der kryptologischen
Schaltung des Chiffrators
1. Allgemeine Aussagen
2. Änderung der Struktur des Zustandsspeichers
3. Änderung der Funktion x
4. Änderung der Festlegung des Anfangszustan-
des U(0)
Kapitel IV Die Untersuchung der Struktur der Chiffierabbildung
Einführung
§1 Die Abbildung ϕ
1. Definition der Abbildung ϕ
2. Bedingungen für die Eineindeutigkeit von ϕ
2.1 Das grundlegende Gleichungssystem
2.2 Notwendige Bedingungen
2.3 Hinreichende Bedingungen
2.4 Die Anzahl der Elemente in PR
3. Fixpunkte
4. Zustandsklassen
4.1 Definition einer Zustandsklasse
4.2 Die Menge {ϕnU}
4.3 Die Mengen {ϕU1 U2} und {ϕ-1ϕU}
5. Der Spezialfall {P0, R0}
§2 Determiniertes Chiffratormodell
1. Definition von Abbildungen
2. Kryptologische Interpretation und elementare
Eigenschaften der Abbildungen
3. Periodizitätseigenschaften
3.1 Periodizität von Folgen
3.2 Die Periode der Folge r
3.3 Die Periode der Folge (Ui)i=0,1,2,…
3.4 Die Periode der Folge (
als Additionsreihe genutzt wird.
3. Prüfung und Blockierung
§2 Das Schlüsselsystem
1. Kurzzeitschlüssel
2. Langzeitschlüssel
3. Reserveschlüssel
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der
kryptologischen Schaltung
2. Festlegung des Schlüsselsystems
3. Grundprinzip der Erzeugung der Folge W
4. Festlegung der Grundstruktur der krypto-
logischen Schaltung II
5. Festlegung der Parameter der kryptolo-
gischen Schaltung II
5.1 Anzahl der internen Arbeitstakte T 350 kHz
pro Übertragungstakt TÜi
5.2 Kurzzeitschlüssel
5.3 Zustandsspeicher U
5.4 Realisierung der Überführungsfunktion
5.5 Verarbeitung von FUi, S1 und S2
5.6 Einstellung des Anfangszustandes U(0)
5.7 Abgriff der Elemente wi von W
§4 Kryptologische Sicherheit im System OPERATION
§5 Änderungsmöglichkeiten der kryptologischen
Schaltung des Chiffrators
1. Allgemeine Aussagen
2. Änderung der Struktur des Zustandsspeichers
3. Änderung der Funktion x
4. Änderung der Festlegung des Anfangszustan-
des U(0)
Kapitel IV Die Untersuchung der Struktur der Chiffierabbildung
Einführung
§1 Die Abbildung ϕ
1. Definition der Abbildung ϕ
2. Bedingungen für die Eineindeutigkeit von ϕ
2.1 Das grundlegende Gleichungssystem
2.2 Notwendige Bedingungen
2.3 Hinreichende Bedingungen
2.4 Die Anzahl der Elemente in PR
3. Fixpunkte
4. Zustandsklassen
4.1 Definition einer Zustandsklasse
4.2 Die Menge {ϕnU}
4.3 Die Mengen {ϕU1 U2} und {ϕ-1ϕU}
5. Der Spezialfall {P0, R0}
§2 Determiniertes Chiffratormodell
1. Definition von Abbildungen
2. Kryptologische Interpretation und elementare
Eigenschaften der Abbildungen
3. Periodizitätseigenschaften
3.1 Periodizität von Folgen
3.2 Die Periode der Folge r
3.3 Die Periode der Folge (Ui)i=0,1,2,…
3.4 Die Periode der Folge ( )a i=0,1,2,…
4. Analytische Abhängigkeiten
§3 Äquivalente Schlüssel
1. Grundlegende Definition
2. Äquivalente Schlüssel bezüglich der
Folge (Ui)i=1,2,…
3. Äquivalente Schlüssel bezüglich UN
4. Äquivalente Schlüssel bezüglich der
Folge (
)a i=0,1,2,…
4. Analytische Abhängigkeiten
§3 Äquivalente Schlüssel
1. Grundlegende Definition
2. Äquivalente Schlüssel bezüglich der
Folge (Ui)i=1,2,…
3. Äquivalente Schlüssel bezüglich UN
4. Äquivalente Schlüssel bezüglich der
Folge ( )i=1,2,…
§4 Stochastische Modelle der Chiffrierabbildung
1. Markowsche Kette
2. Ein anderes Modell
3. Experimentelle Untersuchung der statis-
tischen Eigenschaften der Additionsreihe
Kapitel V Einschätzung der Sicherheit des Chiffrators
Einleitung
§1 Methoden der Bestimmung des Schlüssels
§2 Kryptologische Auswirkungen technischer Fehler
1. Allgemeine Aussagen über technische Fehler
2. Technische Fehler im Chiffrator und bei der
Verarbeitung der Folge W
3. Kryptologisch schlechte Folge FU im Chif-
frator
3.1 Technische Fehler bei der Erzeugung von FU
3.2 Wahrscheinlichkeit gleicher F-Folgen-Ab-
schnitte im Ergebnis von Stromunterbrechung
4. Ausfall des Taktes t104 im Chiffrator und
im Prüf-Chiffrator
5. Verarbeitung fehlerhafter Schlüssel S
6. Technische Fehler in den Prüfbaugruppen,
-bausteinen und Baugruppen B1, B2
§3 Bedienungsfehler und deren Einfluß auf die
kryptologische Sicherheit
1. Mehrmalige Verwendung des gleichen Kurz-
zeitschlüssels S
2. Verwendung fehlerhafter Kurzzeitschlüssel S
3. Sonstige Bedienungsfehler
Zusammenfassung
1. Zusammenfassung der Resultate des Kapitels IV
2. Zusammenfassung der Resultate des Kapitels V
3. Das Schlüsselsystem und kryptologische Reserven
4. Richtungen der weiteren Untersuchungen der
kryptologischen Schaltung
Schlußfolgerungen
Literatur
Einleitung
Das System OPERATION wird entwickelt zur weiteren Automatisierung
des Gesamtkomplexes der Peilung von Funkstellen. Das System
OPERATION soll das System KRISTALL_QUARZ, welches auf der stra-
tegischen Ebene (Fernpeilung) eingesetzt wird, auf der taktischen
Ebene (Nah- und Nächstpeilung) ergänzen.
Das System OPERATION besteht aus einer Zentrale mit:
- einer Apparatur des Fahndungsstabes (2 Fahrzeuge)
- der Apparatur einer halbstationären Funkbeobachtungsstelle
mit max. 20 Horchposten (10 Fahrzeuge)
und mehreren (maximal 20) halbstationären und beweglichen
Peilpunkten (je ein Fahrzeug pro Peilpunkt).
Im einzelnen dient das System folgenden Zwecken:
a) in der Zentrale:
- der Eingabe und Aufbereitung von Kommandos zur Peilung
von Funkstationen;
- der automatischen Auswahl, Übernahme und Aufbereitung von
Kommandos, die über das System KRISTALL-QUARZ empfangen
werden;
- der Übertragung der aufbereiteten Kommandos;
b) in den Peilpunkten:
- dem Empfang und der Anzeige der Kommandos.
Der Prozeß der Übertragung und des Empfangs der Kommandos
verläuft nach folgendem Prinzip:
1. Stellt der Horchfunker eine Funkstation fest, tastet er ihr
wichtigstes Merkmal als Zusatzmitteilung ein (ein Merkmal
aus 100 möglichen).
2. Danach löst er über eine Taste die automatische Messung der
Frequenz der festgestellten Funkstation aus.
3. Die gemessene Frequenz wird automatisch an eine Zentralein-
heit übergeben, wo mittels Korrekturfrequenz automatisch die
vollständige Empfangsfrequenz bestimmt wird. Die vollständige
Empfangsfrequenz und die Zusatzmitteilung werden in der Zen-
traleinheit zwischengespeichert.
4. Von der Zentraleinheit wird dieses Kommando an die Einrich-
tungen zur Kodierung und Chiffrierung übergeben, wo die wei-
tere automatische Aufbereitung für die Übertragung erfolgt.
5. Die Kommandos werden 5 s. lang fortwährend wiederholt über-
tragen, sofern keine Unterbrechung erfolgt durch die notwen-
dig werdende Übertragung eines neuen Kommandos.
6. Die Kommandos gelangen über Leitungen, Kurzwellen- oder
Ultrakurzwellenkanäle zu den Empfangseinrichtungen der
Peilstationen. Hier werden sie automatisch dekodiert, de-
chiffriert und angezeigt.
Das System OPERATION ist für 24-Stunden-Betrieb ausgelegt.
Die zu übermittelnden Kommandos haben einen sehr hohen Geheim-
haltungsgrad, der durch das System OPERATION gehörende Chif-
friersystem gewährleistet werden muß.
Das System OPERATION wird in der DDR im Militärbereich des
Instituts für Regelungstechnik Berlin (IfR) entwickelt. Die
Mitarbeiter des IfR haben gewisse Erfahrungen auf dem Gebiet
der Entwicklung von automatisierten Kommandosystemen.
An der Entwicklung des Systems OPERATION arbeitet im IfR etwa
25 Entwicklungsingenieure. Die TTF für das System OPERATION
[1] wurden im Januar 1971 an das IfR übergeben. Der eigentliche
Beginn der Arbeiten im IfR war Herbst 1971. Im Dezember 1972
stand das AF2-Muster des Systems (die wesentlichsten Appara-
turen für eine Zentrale und zwei Peilpunkte) für die Labor-
erprobung bereit. Zum Ende des Jahres 1973 wird das K5-Muster
(die Apparaturen für eine Zentrale und 4 Peilstationen) fertig-
gestellt. Ab März 1974 ist die operative Erprobung des K5-
Musters vorgesehen. Während der Erprobung werden keine opera-
tiven Kommandos verarbeitet.
Das System OPERATION wurde auf der Grundlage der elektronischen
Bausteintechnik SN 54/74 der Firma Texas Instruments entwickelt.
Das AF2-Muster wurde mit diesen Baustein bestückt. Im K5-Muster
werden schon in größeren Umfang Modulbausteine der DDR-Baustein-
serie KME-10 verarbeitet. Diese Technik wird dann auch zum Bau
der Seriengeräte verwendet. Im Militärbereich des IfR arbeitet
eine Gruppe von Mitarbeitern, die vom ZCO der DDR entsprechend
den Bedingungen für das Chiffrierwesen bestätigt sind, an der
Entwicklung des Chiffriersystems für das System OPERATION.
Zu dieser Gruppe gehören 4 Diplomingenieure, 1 Mechaniker und
eine technische Zeichnerin. Zwischen dem ZCO der DDR und dieser
speziellen Gruppe im IfR besteht eine sehr enge Zusammenarbeit.
Die Arbeiten zur Entwicklung des Chiffriersystems im System
OPERATION wurden faktisch erst im November 1971 begonnen. An
der kryptologischen Entwicklung des Chiffriersystems konnten
im wesentlichen nur zwei Mitarbeiter des ZCO der DDR arbeiten.
Die Konzeption für das Chiffriersystem wurde vom ZCO am
20.12.1971 vorgelegt. Die allgemeine Konzeption der kryptolo-
gischen Schaltung für den Chiffrator (s. z. B. [3], Abb. 5)
wurde am 20.01.1972 festgelegt. Die kryptologische Schaltung
für den Chiffrator des AF2-Musters (s. z. B. [3], Abb. 1)
wurde am 25.05.1972 in allen Einzelheiten bestimmt. An der
Analyse des Chiffrators für das AF2-Muster konnten nur
zwei Genossen des ZCO der DDR arbeiten.
Auf der Beratung zwischen Genossen des ZCO der UdSSR und des
ZCO der DDR, die im Rahmen der Beratung zur Vorstellung des
AF2-Musters von der Gruppe der Koordinierung vom 27.02. -
03.03.1973 in Berlin stattfand, wurde eingeschätzt (s. [4]),
daß der Chiffrator des AF2-Musters die geforderte Sicherheit
nicht gewährleistet.
Die aus Sicht des ZCO der DDR notwendig erscheinenden Änderungen
der kryptologischen Schaltung (s.[5]) wurde am 02.04.1973
festgelegt. An der hier vorliegenden Analyse dieser neuen
kryptologischen Schaltung arbeitete im ZCO der DDR eine Gruppe
mit 5 Diplommathematikern und einem Programmierer. An der Pro-
grammierung der statistischen Kontrolle der Additionsreihe
arbeitete zeitweise noch ein zweiter Programmierer. Er ge-
hörte nicht zur Gruppe. Der Leiter der Gruppe hat die Quali-
fikation, Kandidat der Wissenschaften. Zwei der 5 Mathematiker
haben erst im Jahre 1972 ihr Studium beendet. Der Programmierer
der Gruppe hat in der Programmierung des zur Verfügung stehenden
Rechners vom Typ
)i=1,2,…
§4 Stochastische Modelle der Chiffrierabbildung
1. Markowsche Kette
2. Ein anderes Modell
3. Experimentelle Untersuchung der statis-
tischen Eigenschaften der Additionsreihe
Kapitel V Einschätzung der Sicherheit des Chiffrators
Einleitung
§1 Methoden der Bestimmung des Schlüssels
§2 Kryptologische Auswirkungen technischer Fehler
1. Allgemeine Aussagen über technische Fehler
2. Technische Fehler im Chiffrator und bei der
Verarbeitung der Folge W
3. Kryptologisch schlechte Folge FU im Chif-
frator
3.1 Technische Fehler bei der Erzeugung von FU
3.2 Wahrscheinlichkeit gleicher F-Folgen-Ab-
schnitte im Ergebnis von Stromunterbrechung
4. Ausfall des Taktes t104 im Chiffrator und
im Prüf-Chiffrator
5. Verarbeitung fehlerhafter Schlüssel S
6. Technische Fehler in den Prüfbaugruppen,
-bausteinen und Baugruppen B1, B2
§3 Bedienungsfehler und deren Einfluß auf die
kryptologische Sicherheit
1. Mehrmalige Verwendung des gleichen Kurz-
zeitschlüssels S
2. Verwendung fehlerhafter Kurzzeitschlüssel S
3. Sonstige Bedienungsfehler
Zusammenfassung
1. Zusammenfassung der Resultate des Kapitels IV
2. Zusammenfassung der Resultate des Kapitels V
3. Das Schlüsselsystem und kryptologische Reserven
4. Richtungen der weiteren Untersuchungen der
kryptologischen Schaltung
Schlußfolgerungen
Literatur
Einleitung
Das System OPERATION wird entwickelt zur weiteren Automatisierung
des Gesamtkomplexes der Peilung von Funkstellen. Das System
OPERATION soll das System KRISTALL_QUARZ, welches auf der stra-
tegischen Ebene (Fernpeilung) eingesetzt wird, auf der taktischen
Ebene (Nah- und Nächstpeilung) ergänzen.
Das System OPERATION besteht aus einer Zentrale mit:
- einer Apparatur des Fahndungsstabes (2 Fahrzeuge)
- der Apparatur einer halbstationären Funkbeobachtungsstelle
mit max. 20 Horchposten (10 Fahrzeuge)
und mehreren (maximal 20) halbstationären und beweglichen
Peilpunkten (je ein Fahrzeug pro Peilpunkt).
Im einzelnen dient das System folgenden Zwecken:
a) in der Zentrale:
- der Eingabe und Aufbereitung von Kommandos zur Peilung
von Funkstationen;
- der automatischen Auswahl, Übernahme und Aufbereitung von
Kommandos, die über das System KRISTALL-QUARZ empfangen
werden;
- der Übertragung der aufbereiteten Kommandos;
b) in den Peilpunkten:
- dem Empfang und der Anzeige der Kommandos.
Der Prozeß der Übertragung und des Empfangs der Kommandos
verläuft nach folgendem Prinzip:
1. Stellt der Horchfunker eine Funkstation fest, tastet er ihr
wichtigstes Merkmal als Zusatzmitteilung ein (ein Merkmal
aus 100 möglichen).
2. Danach löst er über eine Taste die automatische Messung der
Frequenz der festgestellten Funkstation aus.
3. Die gemessene Frequenz wird automatisch an eine Zentralein-
heit übergeben, wo mittels Korrekturfrequenz automatisch die
vollständige Empfangsfrequenz bestimmt wird. Die vollständige
Empfangsfrequenz und die Zusatzmitteilung werden in der Zen-
traleinheit zwischengespeichert.
4. Von der Zentraleinheit wird dieses Kommando an die Einrich-
tungen zur Kodierung und Chiffrierung übergeben, wo die wei-
tere automatische Aufbereitung für die Übertragung erfolgt.
5. Die Kommandos werden 5 s. lang fortwährend wiederholt über-
tragen, sofern keine Unterbrechung erfolgt durch die notwen-
dig werdende Übertragung eines neuen Kommandos.
6. Die Kommandos gelangen über Leitungen, Kurzwellen- oder
Ultrakurzwellenkanäle zu den Empfangseinrichtungen der
Peilstationen. Hier werden sie automatisch dekodiert, de-
chiffriert und angezeigt.
Das System OPERATION ist für 24-Stunden-Betrieb ausgelegt.
Die zu übermittelnden Kommandos haben einen sehr hohen Geheim-
haltungsgrad, der durch das System OPERATION gehörende Chif-
friersystem gewährleistet werden muß.
Das System OPERATION wird in der DDR im Militärbereich des
Instituts für Regelungstechnik Berlin (IfR) entwickelt. Die
Mitarbeiter des IfR haben gewisse Erfahrungen auf dem Gebiet
der Entwicklung von automatisierten Kommandosystemen.
An der Entwicklung des Systems OPERATION arbeitet im IfR etwa
25 Entwicklungsingenieure. Die TTF für das System OPERATION
[1] wurden im Januar 1971 an das IfR übergeben. Der eigentliche
Beginn der Arbeiten im IfR war Herbst 1971. Im Dezember 1972
stand das AF2-Muster des Systems (die wesentlichsten Appara-
turen für eine Zentrale und zwei Peilpunkte) für die Labor-
erprobung bereit. Zum Ende des Jahres 1973 wird das K5-Muster
(die Apparaturen für eine Zentrale und 4 Peilstationen) fertig-
gestellt. Ab März 1974 ist die operative Erprobung des K5-
Musters vorgesehen. Während der Erprobung werden keine opera-
tiven Kommandos verarbeitet.
Das System OPERATION wurde auf der Grundlage der elektronischen
Bausteintechnik SN 54/74 der Firma Texas Instruments entwickelt.
Das AF2-Muster wurde mit diesen Baustein bestückt. Im K5-Muster
werden schon in größeren Umfang Modulbausteine der DDR-Baustein-
serie KME-10 verarbeitet. Diese Technik wird dann auch zum Bau
der Seriengeräte verwendet. Im Militärbereich des IfR arbeitet
eine Gruppe von Mitarbeitern, die vom ZCO der DDR entsprechend
den Bedingungen für das Chiffrierwesen bestätigt sind, an der
Entwicklung des Chiffriersystems für das System OPERATION.
Zu dieser Gruppe gehören 4 Diplomingenieure, 1 Mechaniker und
eine technische Zeichnerin. Zwischen dem ZCO der DDR und dieser
speziellen Gruppe im IfR besteht eine sehr enge Zusammenarbeit.
Die Arbeiten zur Entwicklung des Chiffriersystems im System
OPERATION wurden faktisch erst im November 1971 begonnen. An
der kryptologischen Entwicklung des Chiffriersystems konnten
im wesentlichen nur zwei Mitarbeiter des ZCO der DDR arbeiten.
Die Konzeption für das Chiffriersystem wurde vom ZCO am
20.12.1971 vorgelegt. Die allgemeine Konzeption der kryptolo-
gischen Schaltung für den Chiffrator (s. z. B. [3], Abb. 5)
wurde am 20.01.1972 festgelegt. Die kryptologische Schaltung
für den Chiffrator des AF2-Musters (s. z. B. [3], Abb. 1)
wurde am 25.05.1972 in allen Einzelheiten bestimmt. An der
Analyse des Chiffrators für das AF2-Muster konnten nur
zwei Genossen des ZCO der DDR arbeiten.
Auf der Beratung zwischen Genossen des ZCO der UdSSR und des
ZCO der DDR, die im Rahmen der Beratung zur Vorstellung des
AF2-Musters von der Gruppe der Koordinierung vom 27.02. -
03.03.1973 in Berlin stattfand, wurde eingeschätzt (s. [4]),
daß der Chiffrator des AF2-Musters die geforderte Sicherheit
nicht gewährleistet.
Die aus Sicht des ZCO der DDR notwendig erscheinenden Änderungen
der kryptologischen Schaltung (s.[5]) wurde am 02.04.1973
festgelegt. An der hier vorliegenden Analyse dieser neuen
kryptologischen Schaltung arbeitete im ZCO der DDR eine Gruppe
mit 5 Diplommathematikern und einem Programmierer. An der Pro-
grammierung der statistischen Kontrolle der Additionsreihe
arbeitete zeitweise noch ein zweiter Programmierer. Er ge-
hörte nicht zur Gruppe. Der Leiter der Gruppe hat die Quali-
fikation, Kandidat der Wissenschaften. Zwei der 5 Mathematiker
haben erst im Jahre 1972 ihr Studium beendet. Der Programmierer
der Gruppe hat in der Programmierung des zur Verfügung stehenden
Rechners vom Typ Siemens 4004/45
noch wenig Erfahrung. Ana-
lysearbeiten von solcher Art und solchem Umfang wie für den
Chiffrator des Systems OPERATION wurde im ZCO der DDR zum
ersten Male durchgeführt. Für die Entwicklung des Chiffrators
und dessen Analyse gab es praktisch keine eigenen Erfahrungen
im ZCO der DDR. Es mußten und konnten dank der Unterstützung
der Genossen des ZCO der UdSSR in großen Umfang sowjetische
Erfahrungen bei der Bearbeitung der Probleme genutzt werden.
Dennoch konnten Arbeiten für die Analyse nicht vollständig aus-
geführt werden, da dafür zu wenig Zeit und zu wenig qualifi-
zierte Kader zur Verfügung standen.
KAPITEL I
Chiffrierverbindungen im System OPERATION
§1. Schema der Chiffrierverbindungen
Das Schema der Chiffrierverbindungen des Systems OPERATION
zeigt Abbildung 1.1.

Die in der Station C (Zentrale) gebildeten Nachrichten
(Kommandos) werden im Simplexbetrieb an alle Stationen E
(Peilpunkt) zugleich übermittelt.
Der Chiffrierverkehr im System OPERATION ist zirkularer
Verkehr. Die zwei Stationen A gehören zum System KRISTALL-
QUARZ. Nachricht der Stationen A, die in der Station
OPERATION über KRISTALL-QUARZ empfangen werden, werden zur
weiteren Übermittlung an die Stationen E in der Station C
neu chiffriert.
§2. Nachrichten auf dem Übertragungskanal
1. Struktur der Nachrichten
Die Übertragung der Nachrichten von der Station C an die
Station E erfolgt nach dem Start-Stop-Prinzip mit In-
formationsblöcken.
Ein Informationsblock besteht aus 77 Bit und setzt sich
zusammen aus dem Startkode mit 16 Bit (für Blocksynchro-
nisation), dem Geheimtextblock mit 47 Bit, einem Kontroll-
bit für die Aussage "Chiffrierung normal" und der Kode-
sicherung 2 mit 13 Bit.
Ein Geheimtextblock besteht aus dem chiffrierten Grund
textblock mit 47 Bit.
Ein Grundtextblock beseht aus dem Klartexblock mit
41 Bit und der Kodesicherung 1 mit 6 Bit.
Ein Klartextblock enthält eine vollständige Nachricht
(ein vollständiges Kommando) und setzt sich wie folgt
zusammen (s. [7], 2.2.8.1):
Lfd. Nr. Information Bit
1. löschen des Kommandos 1
2. Blendkennung 1
3. frei (festliegend) 4
4. Frequenz (6 Dezimalziffern im
BCD-Kode 2421) 24
5. Zusatzmitteilung (2 Dezimal-
ziffern im BCD-Kode 2421) 8
6. SKP 1
7. Station arbeitet 1
8. Parität 1
(In der angegebenen Reihenfolge wird der Klartextblock
in die Chiffriereinrichtung übergeben und chiffriert.)
Die 4 freien Bit (lfd. Nr. 3) waren ursprünglich auch
als echte Informationsträger vorgesehen. Die Verkürzung
der Klartextblöcke auf 37 Bit bedeutet größere tech-
nische Veränderungen. Eine zufallsmäßige Belegung der 4
festen Bit bzw. ihre unchiffrierte Übertragung kann erst
nach der K5-Entwicklung realisiert werden.
2. Klartexteigenschaften
In den Klartextblöcken treten durch die Darstellung der
8 Dezimalziffern im BCD-Kode 2421 und durch die 4 festen
Bit sehr starke Gesetzmäßigkeiten auf. Es können nur
maximal 108 * 23 verschiedene Klartextblöcke von den
241 ≈ 22 * 1012 theoretische möglichen auftreten.
Bei der Information "löschen des Kommandos" tritt ein
Zeichen von {0, L} häufiger als das andere auf.
3. Nachrichtenübertragung
Zur Senkung der Verlustfehlerwahrscheinlichkeit der
im Simplexbetrieb übertragenen Nachrichten werden
diese mehrfach wiederholt übertragen. Vom Zeitpunkt
der Auslösung einer Nachricht 5 s. lang. Bei den vor-
gesehenen Übertragungsgeschwindigkeiten von 200, 600
und 1200 Bd. bedeutet das die Übertragung von bzw. 13,
39 und 78 unmittelbar aufeinanderfolgenden Informations-
blöcken mit gleichem Grundtextblock. Im System werden
Nachrichten mit drei verschiedenen Rängen übertragen.
Die Übertragung einer Nachricht mit niederem Rang wird
unterbrochen, wenn eine Korrektur der ursprünglichen
Nachricht erfolgt. Die Unterbrechung erfolgt nur am
Ende der Übertragung eines Informationsblockes. Der
erste Informationsblock mit der neuen Nachricht wird
unmittelbar nach dem letzten Informationsblock mit der
alten Nachricht übertragen. Die neue Nachricht wird
wieder 5 s. lang übertragen. Auf dem Nachrichtenkanal
erscheinen nicht die reinen Informationsblöcke.
Zu den je 77 Elementen der Informationsblöcke werden
Bit für Bit addiert mod 2 die Elemente entsprechend
langer Abschnitte einer Synchronisationsfolge F. In
den Zeiten, in denen von der Station C keine Informa-
tionsblöcke übertragen werden, wird nur die Folge F
übertragen.
4. Informationsdichte
Es kann nach den letzten Informationen angenommen werden
(vgl. [8], Pkt. 2.2.3.1), daß die Zeitpunkte der Auslö-
sung einer Nachrichtenübertragung gleichverteilt sind,
wobei folgende Parameter zeitweise gelten:
mittlerer Abstand zwischen zwei Auslösungen 10 s
min Abstand zwischen zwei Auslösungen 1 s
max Abstand zwischen zwei Auslösungen 20 s
5. Blendnachrichten
Zur Verschleierung der Zeitpunkte der Übermittlung
von Nachrichten können im Datensender der Station
C Blendinformationsblöcke gebildet und 5 s lang über-
tragen werden. Die Bildung und Übertragung der Blend-
nachrichten erfolgt automatisch und wird durch Tasten-
druck ausgelöst. Die Blendinformationsblöcke entstehen
aus Blendklartextblöcken analog wie die Informations-
blöcke aus den Klartextblöcken. Ein Blendklartextblock
besteht aus einem Bit Blendkennung und einem Abschnitt
der Länge 40 einer Pseudo-Zufallsfolge B. Blendinfor-
mationsblöcke sind auf dem Kanal nicht von anderen
Informationsblöcken unterscheidbar.
6. Geheimhaltung der Nachrichten
Die Geheimhaltung der übermittelten Nachrichten ist
praktisch für unbegrenzte Zeit zu gewährleisten.
KAPITEL II
Das Chiffriersystem im System OPERATION
§1 Forderungen an das Chiffriersystem
Das Chiffriersystem muß die automatische Chiffrierung bzw.
Dechiffrierung der zu übermittelnden Nachricht gewährleisten.
Chiffrierung und Dechiffrierung müssen innerhalb der insge-
samt zulässigen Übertragungszeit in 0,5 sec erfolgen.
(s. [1] Pkt. 11.1.23, 11.1.24)
Das Chiffriersystem muß die kryptologische Sicherheit der
Nachrichten für praktisch unbegrenzte Zeit gewährleisten,
wobei der Zeitschlüssel nicht mehr als ein bis zwei Mal
täglich gewechselt wird und der Gegner das Chiffriersystem
kennt (s. [2]). Die Vorbereitungszeit für den Schlüssel-
wechsel darf nicht länger als 2 Minuten sein, der Schlüssel-
wechsel selbst muß innerhalb 10 sec erfolgen.
Durch Übermittlung von Blendnachrichten muß es möglich sein,
den Zeitpunkt der Übertragung operativer Nachrichten zu
verschleiern. (s. [4] 4.6.3 u. 11.1.36)
Das Volumen und das Gewicht der Chiffriereinrichtung, be-
sonders die für die Station E, sind möglichst gering zu
halten.
Das Chiffriersystem muß den elektrischen, klimatischen usw.
Forderungen des Gesamtsystems genügen.
§2 Konzeption des Chiffriersystems1)
1) Zur Begründung der Konzeption s. [3], Abschnitt 3.
1. Chiffrierprinzip
In der Station C ist eine Chiffriereinrichtung enthalten.
In jeder Station E ist eine Dechiffriereinrichtung ent-
halten.
Im Chiffriersystem wird ein Additionsverfahren realisiert.
Die Additionsreihen zur Chiffrierung bzw. zur Dechiffrie-
rung werden in der Chiffriereinrichtung und allen Dechif-
friereinrichtungen des Chiffriersystems unter Benutzung
eines Zeitschlüssels S und einer Synchronisationsfolge
F synchron gebildet.
2. Synchronisationsprinzip
In der Chiffriereinrichtung und allen Dechiffriereinrich-
tungen des Chiffriersystems wird ständig im Übertragungs-
takt TÜ = (TÜi) eine rekurrente Folge (fi)
eine rekurrente Folge (fi) (fi ∈ {0,1}, i=1,2,…) Synchron erzeugt. zu diesem Zweck
wird die in der Chiffriereinrichtung erzeugte Folge F
von der Station C ständig an alle Stationen E übermittelt.
In den Zeiten, in denen von der Station C keine Infor-
mationsblöcke übertragen werden, wird die in den Stationen
E empfangene Folge in den Dechiffriereinrichtungen zur
Herstellung bzw. Aufrechterhaltung der Synchronisation
genutzt.
3. Erzeugung der Additionsreihen
Aus der Folge F = (fi)
(fi ∈ {0,1}, i=1,2,…) Synchron erzeugt. zu diesem Zweck
wird die in der Chiffriereinrichtung erzeugte Folge F
von der Station C ständig an alle Stationen E übermittelt.
In den Zeiten, in denen von der Station C keine Infor-
mationsblöcke übertragen werden, wird die in den Stationen
E empfangene Folge in den Dechiffriereinrichtungen zur
Herstellung bzw. Aufrechterhaltung der Synchronisation
genutzt.
3. Erzeugung der Additionsreihen
Aus der Folge F = (fi) und dem Zeitschlüssel S wird
im Übertragungstakt TÜ = (TÜi)
und dem Zeitschlüssel S wird
im Übertragungstakt TÜ = (TÜi) eine Folge
W = (wi)
eine Folge
W = (wi) (wi ∈ {0,1}, i=1,2,…) in Abhängigkeit von den
Chiffrierzeitpunkten (Dechiffrierzeitpunkten) erzeugt.
Zur Chiffrierung der Grundtextblöcke (Dechiffrierung der
Geheimtextblöcke) werden von der Folge W Abschnitte Wi,
Wi+1, …, Wi+46 als Additionsreihen genutzt und mit den
Grundtextblöcken (Geheimtextblöcken) verknüpft.
Die Grundtextblöcke (insbesondere auch gleiche) der auf
dem Übertragungskanal aufeinanderfolgenden Informations-
blöcke werden mit unterschiedlichen Abschnitten der Folge
W (unterschiedlichen Additionsreihen) chiffriert.
Zwischen den jeweils ersten Elementen der Geheimtextblöcke
von zwei unmittelbar aufeinander folgenden Informations-
blöcke besteht ein Abstand von 77 Übertragungstakten.
Wenn der erste Geheimtextblock durch Addition des Grund-
textblockes mit dem Abschnitt Ai = Wi, Wi+, …, Wi+46 von
W entstanden ist, dann ist der folgende Geheimtextblock
durch Addition des gleichen Grundtextblockes mit dem
Abschnitt Ai+77 = Wi+77, Wi+78 … Wi+123 entstanden. Der
Abstand beider W-abschnitte ist 30 Übertragungstakte.
Bei Unterbrechung einer Nachricht durch Übermittlung
einer neuen Nachricht ist der Abstand der jeweils ersten
Elemente des letzten Informationsblöcke mit der alten
Nachricht und des ersten Informationsblockes mit der neuen
Nachricht ebenfalls 77 Übertragungstakte. Entsprechend
ist der Abstand der zur Chiffrierung der aufeinanderfol-
genden unterschiedlichen Grundtextblöcke genutzten Ab-
schnitte von W wiederum 30 Übertragungstakte.
§3 Die Funktionseinheit der Chiffriereinrichtung
1. Schlüsseleingabeeinheit
Der Zeitschlüssel S besteht aus zwei 0,1-Folgen S1 und
S2. Die Schlüsseleingabeeinheit SE besteht aus einem
optoelektronischen Lochkartenleser, zwei Schlüsselspei-
chern SRS1 und SRS2 und Steuer- und Prüfbaugruppen.
Der Zeitschlüssel S ist für die Eingabe auf einer Loch-
karte gespeichert.
Der Zeitschlüssel wird beim Herausziehen der Lochkarte
aus der Eingabeeinheit in die Speicher SRS1 und SRS2
eingelesen.
Wenn der Strom für die Schlüsseleingabeeinheit unter-
brochen wird, werden die Speicher SRS1 und SRS2 gelöscht.
In den Prüfbausteinen der Schlüsseleingabeeinheit werden
die Eingabe des Schlüssels Sund seine Verarbeitung kon-
trolliert. Fehler bei der Eingabe des Schlüssels (Signal
FGSE) werden von Fehlern bei der Verarbeitung des
Schlüssels (M4-SE) unterschieden. Vom Zeitpunkt des Ein-
schaltens des Stromes für die Schlüsseleingabeeinheit oder
vom Zeitpunkt des Beginns der Neueingabe eines Schlüssels
(Schlüsselwechsel) bis zum fehlerfreien Abschluß der Ein-
gabe eines Schlüssels wird das Signal FGSE = 0 erzeugt.
Nur wenn FGSE=L ist (Schlüssel fehlerfrei in SE), kann
das Fehlersignal M4-SE=L erzeugt werden.
In der Steuerbaugruppe der Schlüsseleingabeeinheit wird
aus dem Steuersignal FGFU und dem internen Takt T 350 kHz
der Takt t104 gebildet. Der Takt t104 enthält pro Über-
tratungstakt TUi (i=1,2,…) genau 104 Takte von T 350 kHz.
Mit dem Takt t104 wird die Verarbeitung des Zeitschlüssels S
im Chiffrator und Prüf-Chiffrator gesteuert.
2. Synchronisationseinheit
Die Synchronisationseinheit besteht aus dem F-Generator,
einem Zufallsgenerator, einem Taktgenerator, sowie Steuer-
und Prüfbaugruppen.
Im F-Generator wird die Synchronisationsfolge F = (fi)
(wi ∈ {0,1}, i=1,2,…) in Abhängigkeit von den
Chiffrierzeitpunkten (Dechiffrierzeitpunkten) erzeugt.
Zur Chiffrierung der Grundtextblöcke (Dechiffrierung der
Geheimtextblöcke) werden von der Folge W Abschnitte Wi,
Wi+1, …, Wi+46 als Additionsreihen genutzt und mit den
Grundtextblöcken (Geheimtextblöcken) verknüpft.
Die Grundtextblöcke (insbesondere auch gleiche) der auf
dem Übertragungskanal aufeinanderfolgenden Informations-
blöcke werden mit unterschiedlichen Abschnitten der Folge
W (unterschiedlichen Additionsreihen) chiffriert.
Zwischen den jeweils ersten Elementen der Geheimtextblöcke
von zwei unmittelbar aufeinander folgenden Informations-
blöcke besteht ein Abstand von 77 Übertragungstakten.
Wenn der erste Geheimtextblock durch Addition des Grund-
textblockes mit dem Abschnitt Ai = Wi, Wi+, …, Wi+46 von
W entstanden ist, dann ist der folgende Geheimtextblock
durch Addition des gleichen Grundtextblockes mit dem
Abschnitt Ai+77 = Wi+77, Wi+78 … Wi+123 entstanden. Der
Abstand beider W-abschnitte ist 30 Übertragungstakte.
Bei Unterbrechung einer Nachricht durch Übermittlung
einer neuen Nachricht ist der Abstand der jeweils ersten
Elemente des letzten Informationsblöcke mit der alten
Nachricht und des ersten Informationsblockes mit der neuen
Nachricht ebenfalls 77 Übertragungstakte. Entsprechend
ist der Abstand der zur Chiffrierung der aufeinanderfol-
genden unterschiedlichen Grundtextblöcke genutzten Ab-
schnitte von W wiederum 30 Übertragungstakte.
§3 Die Funktionseinheit der Chiffriereinrichtung
1. Schlüsseleingabeeinheit
Der Zeitschlüssel S besteht aus zwei 0,1-Folgen S1 und
S2. Die Schlüsseleingabeeinheit SE besteht aus einem
optoelektronischen Lochkartenleser, zwei Schlüsselspei-
chern SRS1 und SRS2 und Steuer- und Prüfbaugruppen.
Der Zeitschlüssel S ist für die Eingabe auf einer Loch-
karte gespeichert.
Der Zeitschlüssel wird beim Herausziehen der Lochkarte
aus der Eingabeeinheit in die Speicher SRS1 und SRS2
eingelesen.
Wenn der Strom für die Schlüsseleingabeeinheit unter-
brochen wird, werden die Speicher SRS1 und SRS2 gelöscht.
In den Prüfbausteinen der Schlüsseleingabeeinheit werden
die Eingabe des Schlüssels Sund seine Verarbeitung kon-
trolliert. Fehler bei der Eingabe des Schlüssels (Signal
FGSE) werden von Fehlern bei der Verarbeitung des
Schlüssels (M4-SE) unterschieden. Vom Zeitpunkt des Ein-
schaltens des Stromes für die Schlüsseleingabeeinheit oder
vom Zeitpunkt des Beginns der Neueingabe eines Schlüssels
(Schlüsselwechsel) bis zum fehlerfreien Abschluß der Ein-
gabe eines Schlüssels wird das Signal FGSE = 0 erzeugt.
Nur wenn FGSE=L ist (Schlüssel fehlerfrei in SE), kann
das Fehlersignal M4-SE=L erzeugt werden.
In der Steuerbaugruppe der Schlüsseleingabeeinheit wird
aus dem Steuersignal FGFU und dem internen Takt T 350 kHz
der Takt t104 gebildet. Der Takt t104 enthält pro Über-
tratungstakt TUi (i=1,2,…) genau 104 Takte von T 350 kHz.
Mit dem Takt t104 wird die Verarbeitung des Zeitschlüssels S
im Chiffrator und Prüf-Chiffrator gesteuert.
2. Synchronisationseinheit
Die Synchronisationseinheit besteht aus dem F-Generator,
einem Zufallsgenerator, einem Taktgenerator, sowie Steuer-
und Prüfbaugruppen.
Im F-Generator wird die Synchronisationsfolge F = (fi) (fi ∈ {0,1}, i=1,2,…) erzeugt. F genügt der Rekursion
fi+52 = fi+3 ⊕ fi (i≥1).
Zur Herstellung eines zufälligen Anfangswertes für die
Folge F bei Inbetriebnahme der Chiffriereinrichtung oder
nach Stromausfall wird die Ausgangsfolge Y =
(fi ∈ {0,1}, i=1,2,…) erzeugt. F genügt der Rekursion
fi+52 = fi+3 ⊕ fi (i≥1).
Zur Herstellung eines zufälligen Anfangswertes für die
Folge F bei Inbetriebnahme der Chiffriereinrichtung oder
nach Stromausfall wird die Ausgangsfolge Y = 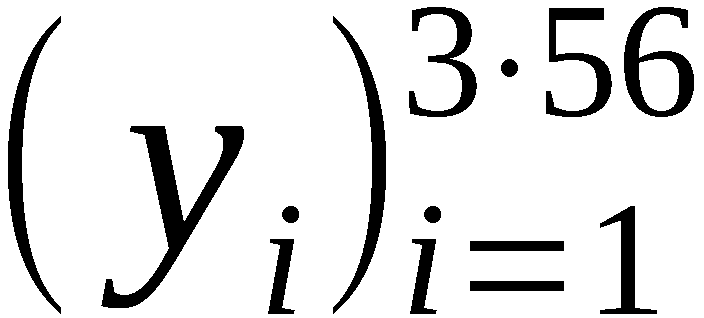 (yi ∈ {0,1}, i=1,2…,3*56) des Zufallsgenerators für
3*56 Übertragungstakte TÜi genutzt:
fi+52 = fi+3 ⊕ fi ⊕ yi (i=1,2, …, 3*56.)
FU = (FUi)
(yi ∈ {0,1}, i=1,2…,3*56) des Zufallsgenerators für
3*56 Übertragungstakte TÜi genutzt:
fi+52 = fi+3 ⊕ fi ⊕ yi (i=1,2, …, 3*56.)
FU = (FUi) abgeleitet. Wenn im Schieberegister des
F-Generators im i-ten Übertragungstakt TÜi (i=1,2,…)
der Abschnitt fifi+1 … fi+51 enthalten ist, so gilt
FUi = (fi+1, fi+2, …, fi+51, fi, fi+1, … fi+51, fi).
Im Taktgenerator wird der interne Takt T 350 kHz erzeugt.
In den Prüfbaugruppen wird die Erzeugung der Folge F
laufende kontrolliert. Während der Erzeugung der zufäl-
ligen Anfangswertes von F wird die Folge
abgeleitet. Wenn im Schieberegister des
F-Generators im i-ten Übertragungstakt TÜi (i=1,2,…)
der Abschnitt fifi+1 … fi+51 enthalten ist, so gilt
FUi = (fi+1, fi+2, …, fi+51, fi, fi+1, … fi+51, fi).
Im Taktgenerator wird der interne Takt T 350 kHz erzeugt.
In den Prüfbaugruppen wird die Erzeugung der Folge F
laufende kontrolliert. Während der Erzeugung der zufäl-
ligen Anfangswertes von F wird die Folge 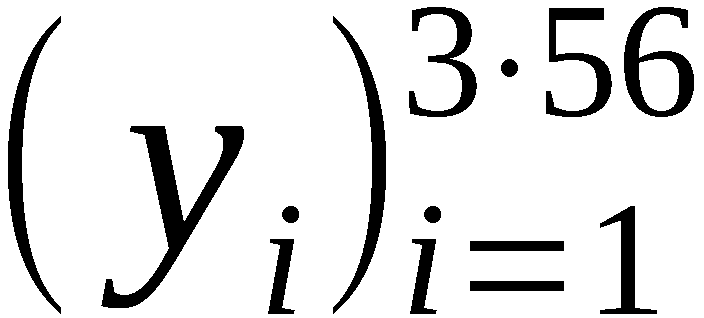 überprüft.
Durch die Steuerbaugruppen wird die Funktion und das Zu-
sammenwirken der anderen Baugruppen der Synchronisations-
einheit gesteuert. Darüberhinaus wird das Steuersignal
FGFU zur Steuerung der Schlüsseleingabeeinheit erzeugt.
3. Chiffrator und Prüf-Chiffrator
Im Chiffrator wird die Folge W = (wi)
überprüft.
Durch die Steuerbaugruppen wird die Funktion und das Zu-
sammenwirken der anderen Baugruppen der Synchronisations-
einheit gesteuert. Darüberhinaus wird das Steuersignal
FGFU zur Steuerung der Schlüsseleingabeeinheit erzeugt.
3. Chiffrator und Prüf-Chiffrator
Im Chiffrator wird die Folge W = (wi) (wi ∈ {0,1}, i=1,2,…)
im Übertragungstakt TÜ = (TÜi)
(wi ∈ {0,1}, i=1,2,…)
im Übertragungstakt TÜ = (TÜi) erzeugt. Wenn im i-ten
Übertragungstakt TÜi (i=1,2…) das erste Additions-
element der Additionsreiche zur Chiffrierung eines Grund-
textblockes erzeugt werden soll, wird der Chiffrator
zum Beginn von TÜi in einen festen bestimmten Anfangs-
zustand
erzeugt. Wenn im i-ten
Übertragungstakt TÜi (i=1,2…) das erste Additions-
element der Additionsreiche zur Chiffrierung eines Grund-
textblockes erzeugt werden soll, wird der Chiffrator
zum Beginn von TÜi in einen festen bestimmten Anfangs-
zustand 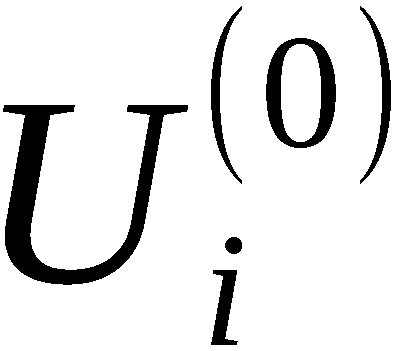 = U(0) gebracht. Unter Einwirkung des Elements
FUi der Folge FU und des Zeitschlüssels S wird dann im
i-ten Übertragungstakt TÜi das Element wi erzeugt. Der
Chiffrator geht dabei aus dem Zustand
= U(0) gebracht. Unter Einwirkung des Elements
FUi der Folge FU und des Zeitschlüssels S wird dann im
i-ten Übertragungstakt TÜi das Element wi erzeugt. Der
Chiffrator geht dabei aus dem Zustand 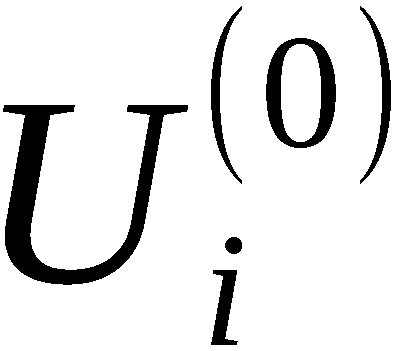 in den Zu-
stand
in den Zu-
stand  über.
Unter Einwirkung des Elements FUi+1 der Folge FU und des
Zeitschlüssels S wird dann im (i+1)ten Übertragungstakt
TÜi+1 das Element wi+1 erzeugt. Der Chiffrator geht dabei
aus dem Zustand
über.
Unter Einwirkung des Elements FUi+1 der Folge FU und des
Zeitschlüssels S wird dann im (i+1)ten Übertragungstakt
TÜi+1 das Element wi+1 erzeugt. Der Chiffrator geht dabei
aus dem Zustand  in den Zustand
in den Zustand 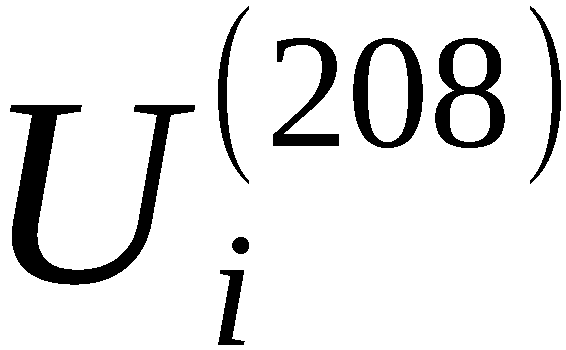 über. Und so
weiter bis zum Übertragungstakt Ti+k (k ∈ {77,78,…}),
in dem wiederum das erste Additionselement der Additions-
reihe zur Chiffrierung eines Grundtextblockes erzeugt
werden soll. Parallel zum Chiffrator wird zum Zweck der
Prüfung des Chiffrators im Prüf-Chiffrator die Folge
W = (wi)
über. Und so
weiter bis zum Übertragungstakt Ti+k (k ∈ {77,78,…}),
in dem wiederum das erste Additionselement der Additions-
reihe zur Chiffrierung eines Grundtextblockes erzeugt
werden soll. Parallel zum Chiffrator wird zum Zweck der
Prüfung des Chiffrators im Prüf-Chiffrator die Folge
W = (wi) erzeugt.
Chiffrator und Prüfchiffrator unterscheiden sich nicht.
w1 wird aus U(0) erzeugt (damit die Prüfung nicht zu
Beginn anspricht).
4. Steuerung
Die Steuerung steuert den Datenaustausch der Chiffrier-
einrichtung mit anderen Funktionseinheiten der Station C
und die internen Betriebsabläufe in der Chiffriereinrich-
tung.
Die Klartextblöcke werden seriell im Übertragungstakt TÜ
vom Datensender der Station C an die Steuerung der Chif-
friereinrichtung übergeben. Die Übergabe wird (sofern im
Datensender kein neuer Klartextblock vorliegt) über einen
Zeitraum von 5 s nach jeweils 77 Übertragungstakten wieder-
holt. In der Steuerung werden aus den Klartextblöcken in
der Kodierung I (zyklischer Kode mit Basispolynom
g(x) = x6+x+I) in die Grundtextblöcke gebildet. Diese
werden dann durch bitweise Addition mod 2 mit der Folge W
zu Geheimtextblöcken verknüpft. Den Geheimtextblöcken wird
am Ende noch ein Prüfbit
erzeugt.
Chiffrator und Prüfchiffrator unterscheiden sich nicht.
w1 wird aus U(0) erzeugt (damit die Prüfung nicht zu
Beginn anspricht).
4. Steuerung
Die Steuerung steuert den Datenaustausch der Chiffrier-
einrichtung mit anderen Funktionseinheiten der Station C
und die internen Betriebsabläufe in der Chiffriereinrich-
tung.
Die Klartextblöcke werden seriell im Übertragungstakt TÜ
vom Datensender der Station C an die Steuerung der Chif-
friereinrichtung übergeben. Die Übergabe wird (sofern im
Datensender kein neuer Klartextblock vorliegt) über einen
Zeitraum von 5 s nach jeweils 77 Übertragungstakten wieder-
holt. In der Steuerung werden aus den Klartextblöcken in
der Kodierung I (zyklischer Kode mit Basispolynom
g(x) = x6+x+I) in die Grundtextblöcke gebildet. Diese
werden dann durch bitweise Addition mod 2 mit der Folge W
zu Geheimtextblöcken verknüpft. Den Geheimtextblöcken wird
am Ende noch ein Prüfbit "Chiffrierung normal" zugeführt.
Die entstehende Datenfolge wird mit einer Verzögerung von
5 1/2 Übertragungstakten von der Steuerung an den Daten-
sender übergeben.
Die in der Synchronisationseinheit erzeugte Folge F wird
über die Steuerung ebenfalls an den Datensender übergeben.
In der Steuerung wird die Erzeugung der Folge W und deren
Verknüpfung mit den Grundtextblöcken, sowie die Erzeugung
der Folge FU und des Steuersignals FGFU auf Fehler geprüft.
In den Baugruppen zur Blockierung werden die Prüfungen
aller Prüfbaugruppen der Chiffriereinrichtung erfaßt und
ausgewertet. Jedes Fehlersignal (M4-… = L, FGSE = 0)
führt zur Blockierung des Geheimtextausganges der Steuerung.
In der Steuerung wird weiter das Fehlersignal M4-CE = M4i-…
gebildet zur Fehlermeldung an den Datensender. Als Folge
von M4-CE = L wird die Übertragung auf dem Übertragungskanal
unterbrochen.
§4 Die Funktionseinheit einer Dechiffriereinrichtung
1. Schlüsseleingabeeinheit
Die Schlüsseleingabeeinheit einer Dechiffriereinrichtung
unterscheidet sich nicht von der Schlüsseleingabeeinheit
der Chiffriereinrichtung.
2. Synchronisationseinheit
In der Synchronisationseinheit wird die Folge F synchron
zu der in der Chiffriereinrichtung des Chiffriersystems
hergestellten Folge F erzeugt. Dazu wir die von der Sta-
tion C empfangene Datenfolge laufend auf Abschnitte der
Länge 108 untersucht, die die Rekursion
fi+52 = fi+3 + fi (i ≥ 1)
genügend. Wenn ein solcher Abschnitt in der Datenfolge
festgestellt wird, wird er zur weiteren Erzeugung von F
genutzt. (Synchronisationsalgorithmus [3], 4.2.)
Aus der Folge F wird ebenso wie in der Synchronisations-
einheit der Chiffriereinrichtung die Folge FU abgeleitet.
Zur Synchronisationseinheit gehört noch ein Taktgenerator
zur Erzeugung des Taktes T 350 kHz.
3. Dechiffrator
Der Dechiffrator der Dechiffriereinrichtung unterscheidet
sich nicht vom Chiffrator der Chiffriereinrichtung.
4. Steuerung
Die Steuerung steuert den Datenaustausch der Dechif-
friereinrichtung mit den anderen Funktionseinheiten der
Station E und die internen Betriebsabläufe in der De-
chiffriereinrichtung.
Die in der Station E empfangene Datenfolge wird seriell
an die Steuerung übergeben. Zu dieser Datenfolge wird die
in der Synchronisationseinheit erzeugte Folge F bit-
weise mod 2 addiert. Die entstehende Datenfolge wird
an den Datenempfänger der Station E übergeben.
Parallel dazu werden die in der entstehenden Datenfolge
(im Datensender) erkannten Geheimtextblöcke in der Steu-
erung dechiffriert, überprüft (Dekodierung 1, Auswertung
des Prüfbit "Chiffrierung normal") und an den Datenem-
pfänger übergeben.
KAPITEL III
Die kryptologische Schaltung des Chiffrators im System OPERATION
(Kryptologische und technische Realisierung des Chiffriersystems)
§1 Beschreibung der kryptologischen Schaltung des Chiffrators
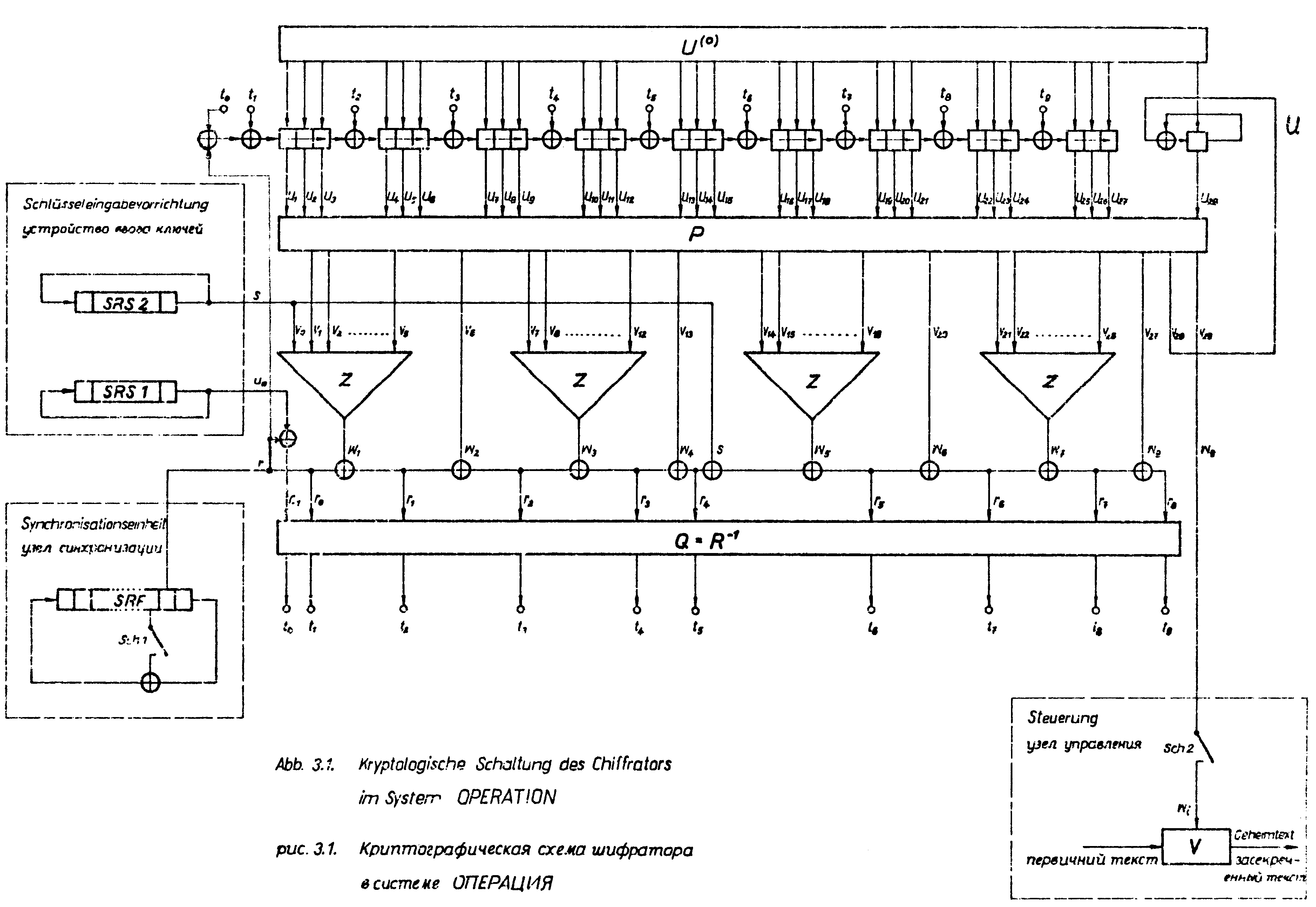
1. Kryptologische Schaltung
Die kryptologischer Schaltung ist in Abbildung 1 dargestellt.
Zeichenerklärung:
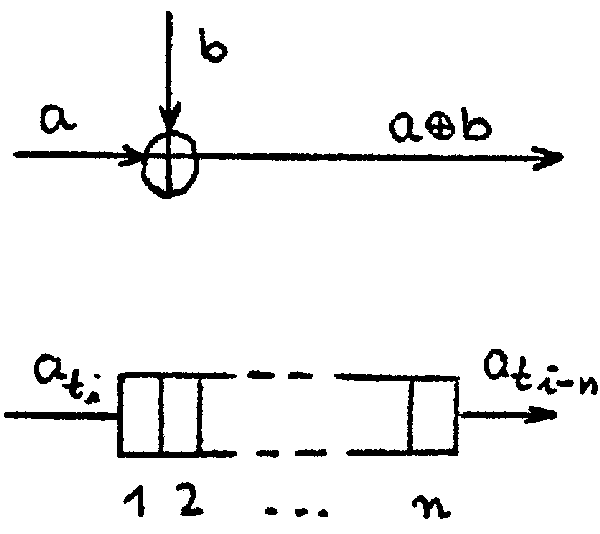 | - Additionselement mod 2 |
| - Speicher der Länge n Verzögerung um n Takte ti |
- U = u1u2…u28 - Zustandsspeicher des Chiffrators
- U(0) - Speicher für den Anfangszustand
U(0) = ( ) ∈ {0,1}28 des Chiffrators
- Z - logische Funktion
Z (e1,e2,…,e6) = 1 ⊕ e1 ⊕ e5 ⊕ e6 ⊕ e14
⊕ e23 ⊕ e25 ⊕ e45 ⊕ e56 ⊕ e134 ⊕ e136
⊕ ⊕ e145 ⊕ e236 ⊕ e246 ⊕ e356 ⊕ e1234
⊕ e1235 ⊕ e1256 ⊕ e2346 ⊕ e12345 ⊕ e13456
(eij…k = ei*ej … ek)
-
) ∈ {0,1}28 des Chiffrators
- Z - logische Funktion
Z (e1,e2,…,e6) = 1 ⊕ e1 ⊕ e5 ⊕ e6 ⊕ e14
⊕ e23 ⊕ e25 ⊕ e45 ⊕ e56 ⊕ e134 ⊕ e136
⊕ ⊕ e145 ⊕ e236 ⊕ e246 ⊕ e356 ⊕ e1234
⊕ e1235 ⊕ e1256 ⊕ e2346 ⊕ e12345 ⊕ e13456
(eij…k = ei*ej … ek)
- 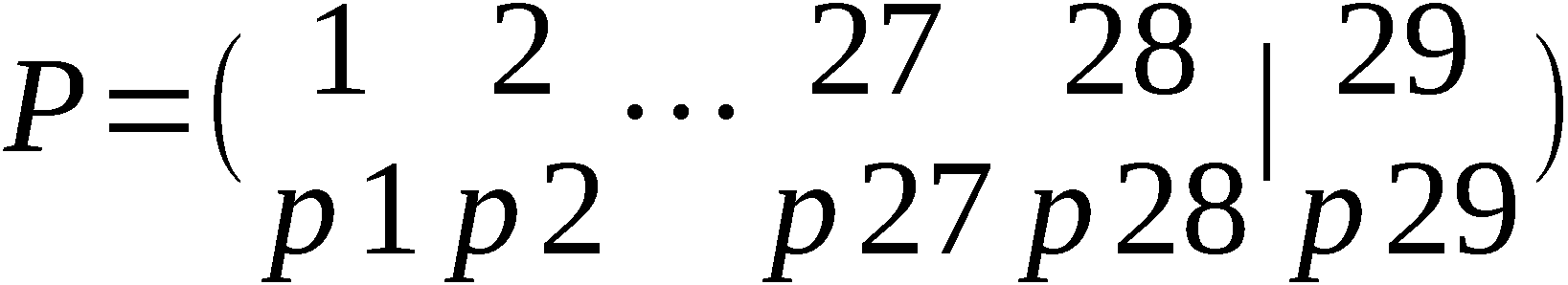 - Kommutator
umkehrbar eindeutige Verknüpfung der Ausgänge Vα von P
mit den Eingängen uPα von P (α = 1,2,…,28) und
von V29 mit uP29 (P29 ∈ {1,2,…,28}).
Durch P wird eine Verknüpfung (Abbildung) der Ausgänge
V1, v2, … v29 von P mit den Eingängen u1, u2, …u28
realisiert. Als Abbildung P : {1,2,…,27,28,29} → {1,2,…,28}
hat P folgende Eigenschaften mindestens eine der beiden
Einschränkungen:
P : {1,2,…,27,28} → {1,2,…,28}
P : {1,2,…,27,29} → {1,2,…,28}
von P ist umkehrbar eindeutig.
-
- Kommutator
umkehrbar eindeutige Verknüpfung der Ausgänge Vα von P
mit den Eingängen uPα von P (α = 1,2,…,28) und
von V29 mit uP29 (P29 ∈ {1,2,…,28}).
Durch P wird eine Verknüpfung (Abbildung) der Ausgänge
V1, v2, … v29 von P mit den Eingängen u1, u2, …u28
realisiert. Als Abbildung P : {1,2,…,27,28,29} → {1,2,…,28}
hat P folgende Eigenschaften mindestens eine der beiden
Einschränkungen:
P : {1,2,…,27,28} → {1,2,…,28}
P : {1,2,…,27,29} → {1,2,…,28}
von P ist umkehrbar eindeutig.
- 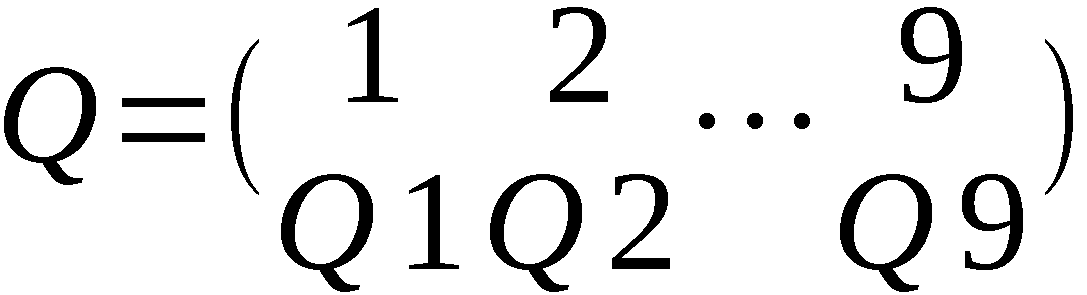 - Kommutator (Permutation 10 x 10)
umkehrbar eindeutige Verknüpfung der Ausgänge tɳ mit
den Eingängen rQɳ-1 (ɳ = 0,1,2,…,9);
- Kommutator (Permutation 10 x 10)
umkehrbar eindeutige Verknüpfung der Ausgänge tɳ mit
den Eingängen rQɳ-1 (ɳ = 0,1,2,…,9);
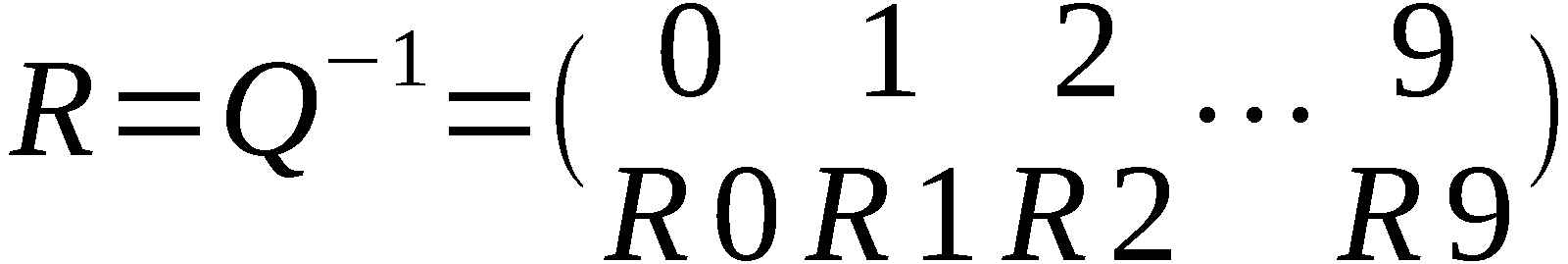 .
.
2. Beschreibung der Erzeugung eines Abschnittes
(wi)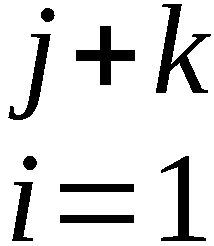 (k > 76) von W = (wi)
(k > 76) von W = (wi) , dessen Anfangs-
abschnitt (wi)
, dessen Anfangs-
abschnitt (wi) als Additionsreihe genutzt wird.
Das Element wj+m (m=0,1…,k) von W wird im (j+m)-ten Über-
gangstakt TÜj+m (Zeitintervall [tj+m, tj+m+1]) erzeugt. Der
Chiffrator befindet sich zu Beginn von TÜj+m im Zustand U(104*m).
U(0) ist der Anfangszustand des Chiffrators. Zu Beginn der
Erzeugung von (wi)
als Additionsreihe genutzt wird.
Das Element wj+m (m=0,1…,k) von W wird im (j+m)-ten Über-
gangstakt TÜj+m (Zeitintervall [tj+m, tj+m+1]) erzeugt. Der
Chiffrator befindet sich zu Beginn von TÜj+m im Zustand U(104*m).
U(0) ist der Anfangszustand des Chiffrators. Zu Beginn der
Erzeugung von (wi)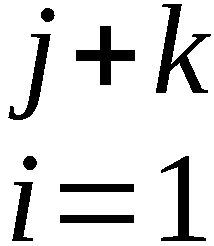 wird der Chiffrator durch
ein Steuersignal in diesen Zustand gebracht. Im
Speicher SRF des F-Generators ist der Abschnitt (fj+m,
fj+m+1,…,fj+m+51) von F mit fj+μ+52 = fj+μ+3⊕fj+μ
(μ = 0,1,…,m-1; (fj, fj+1,…,fj+51) ∈ {0,1}52 - Anfangs-
abschnitt von F zu Beginn von TÜj) enthalten.
In den Speichern SRS1 und SRS2 sind die Folgen S1 =
wird der Chiffrator durch
ein Steuersignal in diesen Zustand gebracht. Im
Speicher SRF des F-Generators ist der Abschnitt (fj+m,
fj+m+1,…,fj+m+51) von F mit fj+μ+52 = fj+μ+3⊕fj+μ
(μ = 0,1,…,m-1; (fj, fj+1,…,fj+51) ∈ {0,1}52 - Anfangs-
abschnitt von F zu Beginn von TÜj) enthalten.
In den Speichern SRS1 und SRS2 sind die Folgen S1 = 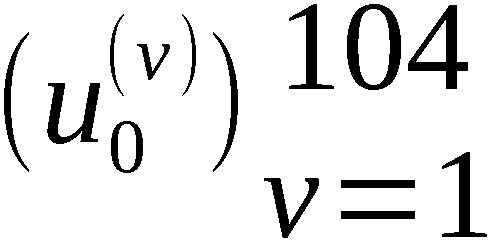 und S2 =
und S2 = 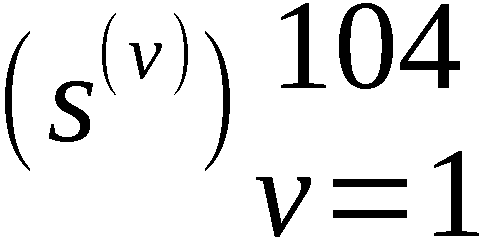 enthalten.
Im Zeitintervall [tj+m, tj+m+1] wird der Chiffrator zusammen
mit den Schieberegistern SRF, SRS1 und SRS2 104 mal im inter-
nen Arbeitstakt T 350 kHz getaktet. Der Chiffrator durchläuft
dabei die Zustände U(104m), U(104*m+1), … U(104*m+104).
Der Inhalt U
enthalten.
Im Zeitintervall [tj+m, tj+m+1] wird der Chiffrator zusammen
mit den Schieberegistern SRF, SRS1 und SRS2 104 mal im inter-
nen Arbeitstakt T 350 kHz getaktet. Der Chiffrator durchläuft
dabei die Zustände U(104m), U(104*m+1), … U(104*m+104).
Der Inhalt U des Speicherelements UP29 von U
wird in der Steuerung als Element wj+m von W verarbeitet.
Der Zustand U(104*m+v-1) (m=0,1,…,k; v =1,2,…,104)
des Chiffrators geht unter der Einwirkung der Eingangs-
kombination
(u
des Speicherelements UP29 von U
wird in der Steuerung als Element wj+m von W verarbeitet.
Der Zustand U(104*m+v-1) (m=0,1,…,k; v =1,2,…,104)
des Chiffrators geht unter der Einwirkung der Eingangs-
kombination
(u , s(v), r(m,v)) (m= 0,1,…,k; v=1,2,…,104)
mit
r(m,v) = r(m,v+52) = fj+m+v (m=0,1,…,k; v=1,2,…,51),
r(m,v) = fj+m (m=0,1,…,k; v=52, 104) j+m (104*m+v)
in den Zustand U(104*m+v) über nach folgender Vorschrift: (3.1):
, s(v), r(m,v)) (m= 0,1,…,k; v=1,2,…,104)
mit
r(m,v) = r(m,v+52) = fj+m+v (m=0,1,…,k; v=1,2,…,51),
r(m,v) = fj+m (m=0,1,…,k; v=52, 104) j+m (104*m+v)
in den Zustand U(104*m+v) über nach folgender Vorschrift: (3.1):

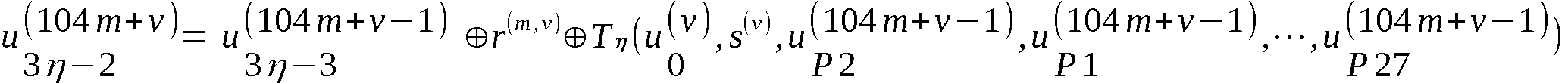 (ɳ=2,3,…,9),
(ɳ=2,3,…,9),
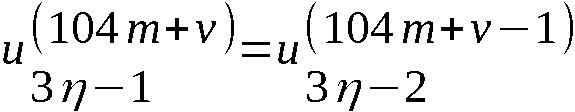 (ɳ=1,2,…,9),
(ɳ=1,2,…,9),
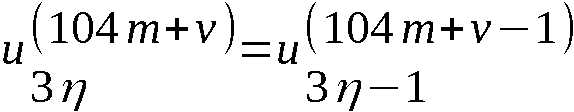 ,
,
 .
Dabei sind die Tɳ = Tɳ(e0,e1,…e28) (ɳ=0,1,…,9) in
(3.1) logische Funktionen mit
TR0 = e0
TR1 = 0
TR2 = Z(e1,e2,…,e6)
TR3 = TR2 + e7
TR4 = TR3 + Z(e8,e9,…,e13)
TR5 = TR4 + e14
TR6 = TR5 + Z(e15, e16,…,e20) + e1
TR7 = TR6 + e21
TR8 = TR7 + Z(e22, e23,…,e27)
TR9 = TR8 + e28
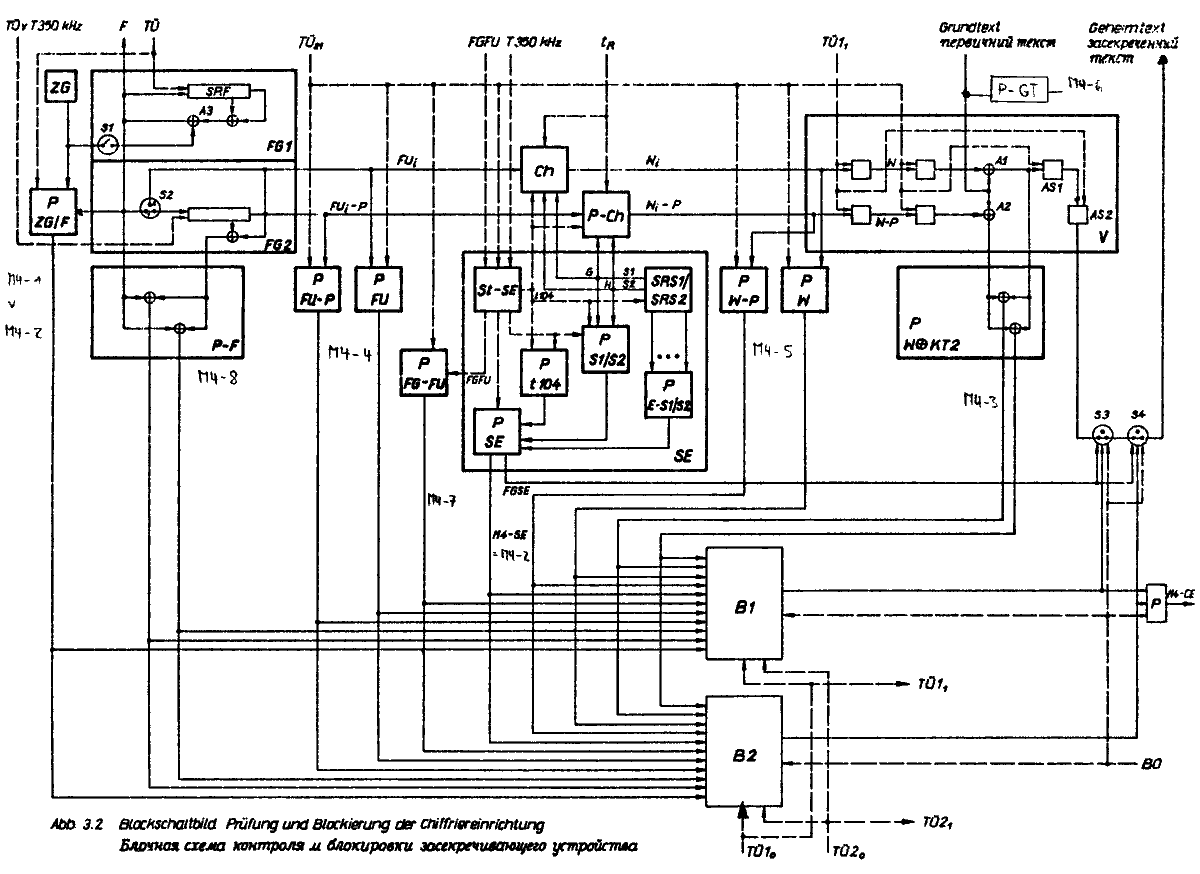
3. Prüfung und Blockierung
Abbildung 3.2 zeigt das Blockschaltbild der Prüfung und
Blockierung der Chiffriereinrichtung.
In der Baugruppe FG1 wird die Folge F erzeugt im Über-
tragungstakte TÜ und gleichzeitig dazu in die Baugruppe
FG2 eingegeben (Schalter S2 in Stellung 1). Aus dem in
FG2 jeweils gespeicherten Abschnitt von F (i=1,2,…)
wird im Takt T 350 kHz die Folge FUi gebildet (Schalter
S2 Stellung 2). In der Prüfbaugruppe P-ZG/F wird die in
FG1 erzeugte Folge F laufend auf konstante Abschnitte der
Länge 56 überprüft. Im Prüfbaustein P-F werden parallel
die in FG1 und FG2 erzeugten Folgen F verglichen. In den
Prüfbausteinen P-FU und P-FU-P wird überprüft, ob die
Folgen FUi oder FUi-P (i=1,2,…) konstant sind.
.
Dabei sind die Tɳ = Tɳ(e0,e1,…e28) (ɳ=0,1,…,9) in
(3.1) logische Funktionen mit
TR0 = e0
TR1 = 0
TR2 = Z(e1,e2,…,e6)
TR3 = TR2 + e7
TR4 = TR3 + Z(e8,e9,…,e13)
TR5 = TR4 + e14
TR6 = TR5 + Z(e15, e16,…,e20) + e1
TR7 = TR6 + e21
TR8 = TR7 + Z(e22, e23,…,e27)
TR9 = TR8 + e28
3. Prüfung und Blockierung
Abbildung 3.2 zeigt das Blockschaltbild der Prüfung und
Blockierung der Chiffriereinrichtung.
In der Baugruppe FG1 wird die Folge F erzeugt im Über-
tragungstakte TÜ und gleichzeitig dazu in die Baugruppe
FG2 eingegeben (Schalter S2 in Stellung 1). Aus dem in
FG2 jeweils gespeicherten Abschnitt von F (i=1,2,…)
wird im Takt T 350 kHz die Folge FUi gebildet (Schalter
S2 Stellung 2). In der Prüfbaugruppe P-ZG/F wird die in
FG1 erzeugte Folge F laufend auf konstante Abschnitte der
Länge 56 überprüft. Im Prüfbaustein P-F werden parallel
die in FG1 und FG2 erzeugten Folgen F verglichen. In den
Prüfbausteinen P-FU und P-FU-P wird überprüft, ob die
Folgen FUi oder FUi-P (i=1,2,…) konstant sind.
Schalter S1 wird nur unmittelbar nach Einschalten des
Stromes für die Chiffriereinrichtung für genau 168 Takte
(TÜ1)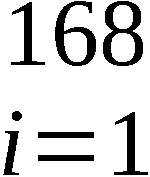 geschlossen. Die im Zufallsgenerator ZG erzeugte
Folge (yi)
geschlossen. Die im Zufallsgenerator ZG erzeugte
Folge (yi)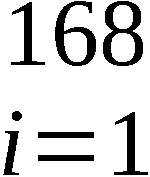 erzeugt im Speicher SRF von FG1 einen zu-
fälligen Anfangswert.
Der Zufallsgenerator wird nur unmittelbar nach dem Ein-
schalten des Stromes in der Prüfbaugruppe P-ZG/F über-
prüft. Die Folge (yi)
erzeugt im Speicher SRF von FG1 einen zu-
fälligen Anfangswert.
Der Zufallsgenerator wird nur unmittelbar nach dem Ein-
schalten des Stromes in der Prüfbaugruppe P-ZG/F über-
prüft. Die Folge (yi)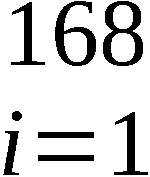 wird als ausreichend zufällig,
angesehen, wenn gilt
wird als ausreichend zufällig,
angesehen, wenn gilt
Die richtige Funktion von P-ZG/F und vom Additionselement
A3 wird überprüft durch Addition einer konstanten Folge
L≡1 anstelle der Zufallsfolge (yi). Die Addition
von L wird durch Drücken einer entsprechenden Prüftaste
ausgelöst. Im Chiffrator Ch und Prüfchiffrator P-Ch werden
die Signale FU oder FU-P, t104, S=(S1,S2) und tR verarbei-
tet. (tR ist das Steuersignal, mit dem Chiffrator und
Prüf-Chiffrator in den Anfangszustand U(0) gebracht werden)
Der in der Steuerungsbaugruppe St-SE der Schlüsselein-
gabeeinheit aus FGFU und T 350 kHz gebildete Takt t104
wird im Prüfbaustein P-t104 daraufhin überprüft, ob pro
Übertragungstakt TÜi genau 104 Takte von t104 vorhanden
sind. Im Prüfbaustein P-S1/S2 wird überprüft, ob für S1
und S2 die Bedingung
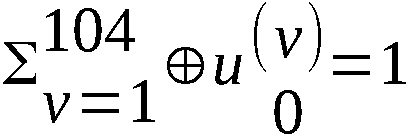 ,
, erfüllt ist. (s. auch Kap. III, §2.).
Im Prüfbaustein P-E-S1/S2 wird nur bei der Eingabe des
Schlüssels S in SRS1/SRS2 überprüft, ob die Bedingungen
erfüllt ist. (s. auch Kap. III, §2.).
Im Prüfbaustein P-E-S1/S2 wird nur bei der Eingabe des
Schlüssels S in SRS1/SRS2 überprüft, ob die Bedingungen
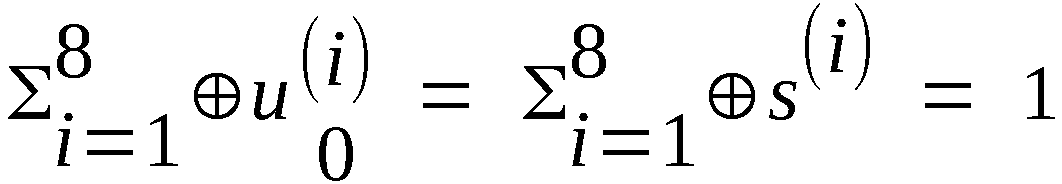
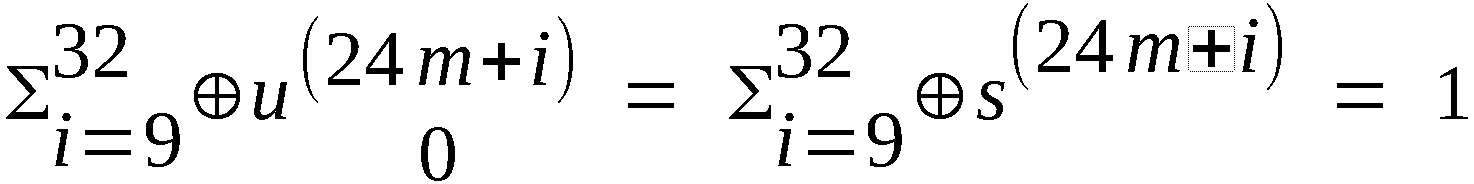 (m = 0, 1, 2, 3)
erfüllt sind.
Im Baustein P-SE werden entsprechend der Eingabesituation
des Schlüssels S (Eingabe richtig abgeschlossen oder nicht)
die Signale FGSE und M4-SE gebildet (s. Kap. II, §3, 1.).
Ein in P-t104 oder P-S1/S2 erkannter Fehler führt immer
entweder zu FGSE = 0 oder M4-SE = L.
Ein in P-E-S1/S2 erkannter Fehler führt immer dazu, daß
FGSE=0 nicht aufgehoben wird.
Im Prüfbaustein P-FGFU wird überprüft, ob pro Übertragungs-
takt ein endliches Freigabesignal übernommen wird.
Vom Chiffrator und vom Prüf-Chiffrator werden in jedem
Übertragungstakt FÜ1 (i=1,2,…) die Folgen Wi und Wi-P
der 105 Speicherinhalte des Speicherelements uP29 von U
an die Baugruppe der Steuerung V übergeben. In den Prüf-
bausteinen P-W und P-W-P werden diese Folgen Wi und Wi-P
auf Konstanz überprüft.
Im Prüfbaustein P-W ⊕ KT2 werden die Ausgänge der
Additionselemente A1 und A2 verglichen. (Damit wird auch
das Additionselement A1, in dem der kodierte Klartext
(Grundtextblöcke KT2) mit der Folge W verknüpft wird,
überprüft.)
Die Fehlersignale aller Prüfbaugruppen und -bausteine
(außer FGSE) werden in den zwei parallelen Baugruppen
B1 und B2 erfaßt. Durch B1 wird der Geheimtextausgang
über den Schalter S2, durch B2 über den Schalter S4 bei
Auftreten eines beliebigen Fehlersignals gesperrt. Das
Fehlersignal FGSE = 0 führt direkt zur Blockierung des
Geheimtextausgangs.
Das Fehlersignal M4-CE führt zur Unterbrechung der Über-
tragung auf dem Kanal.
Die Prüfbaugruppen und -bausteine P-… und B1 und B2
werden durch die Taktsignale TÜ1 und TÜ2 (Übertragungs-
takte) gesteuert.
Durch das Signal B0 (zentral auf Bedienpult auslösbar)
werden die Fehlerspeicher von B1 und B2 (außer bei Feh-
lersignalen von P-ZG/F oder P-SE) zurückgestellt, d. h.
die Blockierung des Geheimtextausganges wird aufgehoben.
Das Signal B0 führt für die Dauer seiner Auslösung in
der Chiffriereinrichtung zur Blockierung des Geheimtext-
ausganges über die Schalter S3 und S4.
§2 Das Schlüsselsystem
1. Kurzzeitschlüssel
Der Kurzzeitschlüssel S = (S1,S2) besteht aus den beiden
Folgen
S1 =
(m = 0, 1, 2, 3)
erfüllt sind.
Im Baustein P-SE werden entsprechend der Eingabesituation
des Schlüssels S (Eingabe richtig abgeschlossen oder nicht)
die Signale FGSE und M4-SE gebildet (s. Kap. II, §3, 1.).
Ein in P-t104 oder P-S1/S2 erkannter Fehler führt immer
entweder zu FGSE = 0 oder M4-SE = L.
Ein in P-E-S1/S2 erkannter Fehler führt immer dazu, daß
FGSE=0 nicht aufgehoben wird.
Im Prüfbaustein P-FGFU wird überprüft, ob pro Übertragungs-
takt ein endliches Freigabesignal übernommen wird.
Vom Chiffrator und vom Prüf-Chiffrator werden in jedem
Übertragungstakt FÜ1 (i=1,2,…) die Folgen Wi und Wi-P
der 105 Speicherinhalte des Speicherelements uP29 von U
an die Baugruppe der Steuerung V übergeben. In den Prüf-
bausteinen P-W und P-W-P werden diese Folgen Wi und Wi-P
auf Konstanz überprüft.
Im Prüfbaustein P-W ⊕ KT2 werden die Ausgänge der
Additionselemente A1 und A2 verglichen. (Damit wird auch
das Additionselement A1, in dem der kodierte Klartext
(Grundtextblöcke KT2) mit der Folge W verknüpft wird,
überprüft.)
Die Fehlersignale aller Prüfbaugruppen und -bausteine
(außer FGSE) werden in den zwei parallelen Baugruppen
B1 und B2 erfaßt. Durch B1 wird der Geheimtextausgang
über den Schalter S2, durch B2 über den Schalter S4 bei
Auftreten eines beliebigen Fehlersignals gesperrt. Das
Fehlersignal FGSE = 0 führt direkt zur Blockierung des
Geheimtextausgangs.
Das Fehlersignal M4-CE führt zur Unterbrechung der Über-
tragung auf dem Kanal.
Die Prüfbaugruppen und -bausteine P-… und B1 und B2
werden durch die Taktsignale TÜ1 und TÜ2 (Übertragungs-
takte) gesteuert.
Durch das Signal B0 (zentral auf Bedienpult auslösbar)
werden die Fehlerspeicher von B1 und B2 (außer bei Feh-
lersignalen von P-ZG/F oder P-SE) zurückgestellt, d. h.
die Blockierung des Geheimtextausganges wird aufgehoben.
Das Signal B0 führt für die Dauer seiner Auslösung in
der Chiffriereinrichtung zur Blockierung des Geheimtext-
ausganges über die Schalter S3 und S4.
§2 Das Schlüsselsystem
1. Kurzzeitschlüssel
Der Kurzzeitschlüssel S = (S1,S2) besteht aus den beiden
Folgen
S1 = 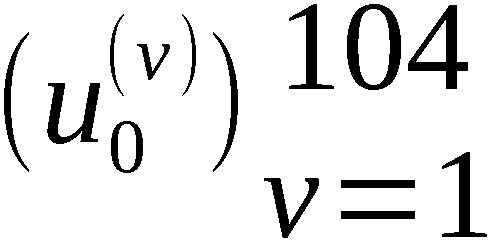 ,
S =
,
S = 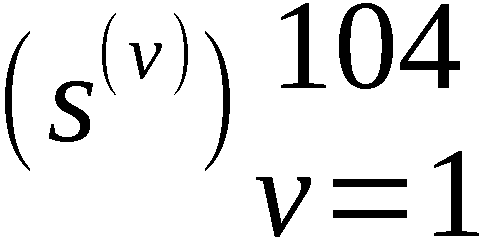 u
u , S(v) ∈{0,1} , v = 1, 2, …, 104).
Zur Herstellung des Kurzzeitschlüssels werden irreguläre
Dualfolgen verwendet. Die Irregularität der Dualfolge
wird durch Überprüfung mit den Kriterien gesichert, die
auch bei der Herstellung irregulärer Dualfolgen für
Schlüsselverfahren angewendet werden. Unterschiedliche
Schlüssel werden aus voneinander unabhängigen irregulären
Dualfolgen hergestellt.
Als Abschnitte
, S(v) ∈{0,1} , v = 1, 2, …, 104).
Zur Herstellung des Kurzzeitschlüssels werden irreguläre
Dualfolgen verwendet. Die Irregularität der Dualfolge
wird durch Überprüfung mit den Kriterien gesichert, die
auch bei der Herstellung irregulärer Dualfolgen für
Schlüsselverfahren angewendet werden. Unterschiedliche
Schlüssel werden aus voneinander unabhängigen irregulären
Dualfolgen hergestellt.
Als Abschnitte
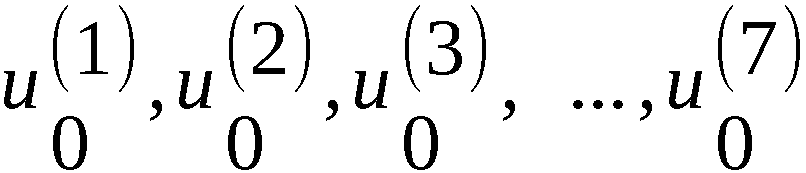
 (m = 0, 1, 2, 3),
S(1), S(2), …, S(7).
S(24m+9), S(24m+10), …, S(24m+31) (m = 0, 1, 2, 3),
von S werden aus der irregulären Dualfolge voneinander
unabhängige Abschnitt der Länge 23 bzw. 7 genommen. Die
fehlenden Elemente von S werden gebildet durch die
Vorschrift.
(m = 0, 1, 2, 3),
S(1), S(2), …, S(7).
S(24m+9), S(24m+10), …, S(24m+31) (m = 0, 1, 2, 3),
von S werden aus der irregulären Dualfolge voneinander
unabhängige Abschnitt der Länge 23 bzw. 7 genommen. Die
fehlenden Elemente von S werden gebildet durch die
Vorschrift.
 ⊕ u
⊕ u
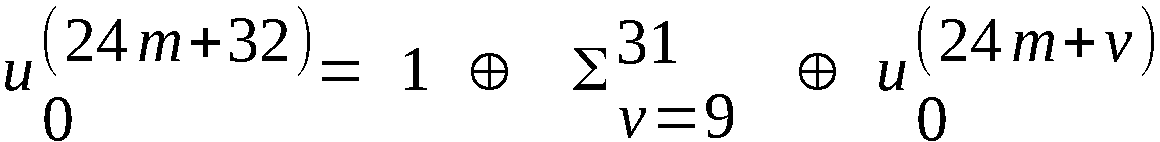 (m = 0, 1, 2, 3)
(m = 0, 1, 2, 3)
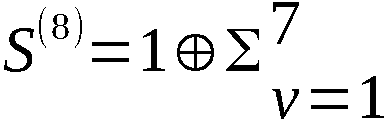 ⊕ S(v)
⊕ S(v)
 ⊕ S(24m+v) (m = 0, 1, 2, 3)
Der Kurzzeitschlüsselvorrat ist 2198 > 1059.
Es ist vorgesehen, den Schlüssel S als Tagesschlüssel
zu benutzen.
2. Langzeitschlüssel
Die Relation P und Q und der Anfangszustand U(0) des
Chiffrators bilden den Langzeitschlüssel (P,Q,U(0)).
Er kann im Ergebnis der kryptologischen Analyse des Chif-
frators für verschiedene Anlagen OPERATION in verschiedenen
Schlüsselbereichen festgelegt werden.
Ein Wechsel des Langzeitschlüssel ist nur in Ausnahme-
fällen (Kompromittierung des Langzeitschlüssels) vorge-
sehen.
Die Relation P ist auf einer Leiterplatte und die Re-
lation Q ist zusammen mit dem Anfangszustand U(0)
auf einer zweiten Leiterplatte durch eingelötete Draht-
brücken realisiert.
3. Reserveschlüssel
Der Langzeitschlüssel oder Elemente des Langzeitschlüssels
können unter Berücksichtigung des technischen Aufwandes
bedingt auch als Kurzzeitschlüssel verwendet werden.
Der Schlüsselvorrat für die Elemente P,Q und U(0) dieses
Reserveschlüssels ist aus kryptologischen und technischen
Gründen beschränkt.
Der Elementevorrat für P ist 28!*28.
Der Elementevorrat für Q ist 10!.
Die Anzahl der technisch möglichen Anfangszustände U(0)
des Chiffrators ist
⊕ S(24m+v) (m = 0, 1, 2, 3)
Der Kurzzeitschlüsselvorrat ist 2198 > 1059.
Es ist vorgesehen, den Schlüssel S als Tagesschlüssel
zu benutzen.
2. Langzeitschlüssel
Die Relation P und Q und der Anfangszustand U(0) des
Chiffrators bilden den Langzeitschlüssel (P,Q,U(0)).
Er kann im Ergebnis der kryptologischen Analyse des Chif-
frators für verschiedene Anlagen OPERATION in verschiedenen
Schlüsselbereichen festgelegt werden.
Ein Wechsel des Langzeitschlüssel ist nur in Ausnahme-
fällen (Kompromittierung des Langzeitschlüssels) vorge-
sehen.
Die Relation P ist auf einer Leiterplatte und die Re-
lation Q ist zusammen mit dem Anfangszustand U(0)
auf einer zweiten Leiterplatte durch eingelötete Draht-
brücken realisiert.
3. Reserveschlüssel
Der Langzeitschlüssel oder Elemente des Langzeitschlüssels
können unter Berücksichtigung des technischen Aufwandes
bedingt auch als Kurzzeitschlüssel verwendet werden.
Der Schlüsselvorrat für die Elemente P,Q und U(0) dieses
Reserveschlüssels ist aus kryptologischen und technischen
Gründen beschränkt.
Der Elementevorrat für P ist 28!*28.
Der Elementevorrat für Q ist 10!.
Die Anzahl der technisch möglichen Anfangszustände U(0)
des Chiffrators ist
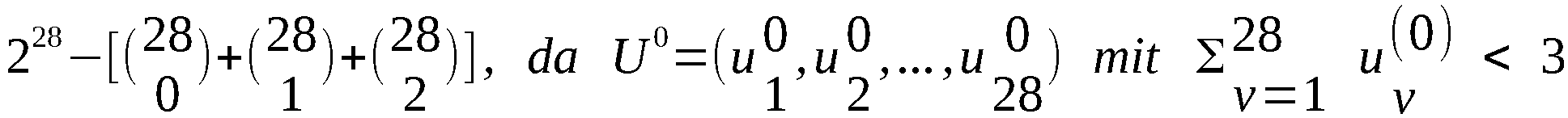 technisch nicht realisierbar ist.
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der kryptologischen Schaltung
Ausgehend von den Forderungen zur Entwicklung eines Chif-
friersystems für das System OPERATION wurde eine krypto-
logische Schaltung I für den Chiffrator entwickelt. Diese
kryptologische Schaltung ist in [3] beschrieben und be-
gründet.
Nach einer ersten vorläufigen Analyse dieser kryptolo-
gischen Schaltung I durch das ZCO der UdSSR (siehe [4])
wurde festgestellt, daß die kryptologische Sicherheit
der Nachrichten bei dieser Schaltung nicht gewährleistet
ist.
Als wesentliche Schwächen wurden erkannt (siehe [4]):
(1) die geringe effektive Schlüsselvorrat;
(2) die ungleichmäßige Mächtigkeit der Klassen äquiva-
lenter Schlüssel;
(3) die Existenz einer großen Anzahl von Schlüsseln, die
inbezug auf die statistischen Eigenschaften der den
Prozeß der Zustandsänderung des Chiffrators beschrei-
benden Markoffschen Kette und damit vermutlich auch
in Bezug auf die statistische Eigenschaften der Ad-
ditionsreihen, schlecht sind.
Die Überwindung dieser schwächen unter Beibehaltung der
wesentlichen Festlegungen der Konzeption des Chiffrier-
systems und des Volumens insbesondere für die Dechif-
friereinrichtung, war der Ausgangspunkt für die Ent-
wicklung der kryptologischen Schaltung des Chiffrators
in der jetzt vorliegenden Gestalt (Schaltung II).
2. Festlegung des Schlüsselsystems
Die gegenwärtig verfügbaren Kommutatoren sind aufgrund
ihrer mechanischen, elektrischen und klimatischen Eigen-
schaften oder aufgrund ihres großen Volumens als Schlüs-
seleingabevorrichtungen für den Einsatz in den Chiffrier-
und Dechiffriereinrichtungen des Systems OPERATION nicht
geeignet.
Es besteht gegenwärtig auch keine Aussicht, einsatzfähige
Kommutatoren in entsprechend kurzer Zeit zu entwickeln.
Kommutatoren sind deshalb im Prinzip zur Zeit nur zur
Realisierung von Langzeitschlüsseln geeignet.
Im Gegensatz dazu war es möglich, in relativ kurzer Zeit
eine optoelektronische Vorrichtung zur Einspeicherung von
0,1-Folgen zu entwickeln, die die Forderungen an eine
Schlüsseleingabevorrichtung im Chiffriersystem von
OPERATION erfüllt.
Ausgehend von diesen technischen Bedingungen wurde fest-
gelegt, 0,1-Folgen als Kurzzeitschlüssel zu benutzen.
Zur Erhöhung der kryptologischen Sicherheit des Chiffrators
erscheint es günstig, diesen Kurzzeitschlüssel mit einem
Langzeitschlüssel, speziell mit einem durch Kommutatoren
realisierten Langzeitschlüssel, zu kombinieren.
3. Grundprinzip der Erzeugung der Folge W
In der vorläufigen Analyse der kryptologischen Schaltung I
wurde festgelegt, daß die in dieser Schaltung realisierte
Umformung der Eingangsfolge FUi (i=1,2,…) hinreichend
kompliziert ist (siehe [4]).
Deshalb konnte bei der Entwicklung der kryptologischen
Schaltung II am Prinzip der Erzeugung der Folge W, wie
es in der Schaltung I realisiert wird, festgehalten
werden: Erzeugung eines Elements wi von W im i-ten
Übertragungstakt durch n-malige rückgekoppelte Umformung
des Inhalts im Zustandsspeicher U des Chiffrators unter
Einwirkung des Abschnittes (fi,fi+1, …, fi+51) von F
und in Abhängigkeit vom Kurzzeitschlüssel S.
4. Festlegung der Grundstruktur der kryptologischen Schaltung II
Ausgehend von der Festlegung des Schlüsselsystems und
der Beibehaltung des Grundprinzips der Erzeugung der
Folge W wurde in Anlehnung an die Struktur der Schaltung I
für die kryptologische Schaltung II die in Abb. 3.3 dar-
gestellte Grundstruktur festgelegt.
technisch nicht realisierbar ist.
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der kryptologischen Schaltung
Ausgehend von den Forderungen zur Entwicklung eines Chif-
friersystems für das System OPERATION wurde eine krypto-
logische Schaltung I für den Chiffrator entwickelt. Diese
kryptologische Schaltung ist in [3] beschrieben und be-
gründet.
Nach einer ersten vorläufigen Analyse dieser kryptolo-
gischen Schaltung I durch das ZCO der UdSSR (siehe [4])
wurde festgestellt, daß die kryptologische Sicherheit
der Nachrichten bei dieser Schaltung nicht gewährleistet
ist.
Als wesentliche Schwächen wurden erkannt (siehe [4]):
(1) die geringe effektive Schlüsselvorrat;
(2) die ungleichmäßige Mächtigkeit der Klassen äquiva-
lenter Schlüssel;
(3) die Existenz einer großen Anzahl von Schlüsseln, die
inbezug auf die statistischen Eigenschaften der den
Prozeß der Zustandsänderung des Chiffrators beschrei-
benden Markoffschen Kette und damit vermutlich auch
in Bezug auf die statistische Eigenschaften der Ad-
ditionsreihen, schlecht sind.
Die Überwindung dieser schwächen unter Beibehaltung der
wesentlichen Festlegungen der Konzeption des Chiffrier-
systems und des Volumens insbesondere für die Dechif-
friereinrichtung, war der Ausgangspunkt für die Ent-
wicklung der kryptologischen Schaltung des Chiffrators
in der jetzt vorliegenden Gestalt (Schaltung II).
2. Festlegung des Schlüsselsystems
Die gegenwärtig verfügbaren Kommutatoren sind aufgrund
ihrer mechanischen, elektrischen und klimatischen Eigen-
schaften oder aufgrund ihres großen Volumens als Schlüs-
seleingabevorrichtungen für den Einsatz in den Chiffrier-
und Dechiffriereinrichtungen des Systems OPERATION nicht
geeignet.
Es besteht gegenwärtig auch keine Aussicht, einsatzfähige
Kommutatoren in entsprechend kurzer Zeit zu entwickeln.
Kommutatoren sind deshalb im Prinzip zur Zeit nur zur
Realisierung von Langzeitschlüsseln geeignet.
Im Gegensatz dazu war es möglich, in relativ kurzer Zeit
eine optoelektronische Vorrichtung zur Einspeicherung von
0,1-Folgen zu entwickeln, die die Forderungen an eine
Schlüsseleingabevorrichtung im Chiffriersystem von
OPERATION erfüllt.
Ausgehend von diesen technischen Bedingungen wurde fest-
gelegt, 0,1-Folgen als Kurzzeitschlüssel zu benutzen.
Zur Erhöhung der kryptologischen Sicherheit des Chiffrators
erscheint es günstig, diesen Kurzzeitschlüssel mit einem
Langzeitschlüssel, speziell mit einem durch Kommutatoren
realisierten Langzeitschlüssel, zu kombinieren.
3. Grundprinzip der Erzeugung der Folge W
In der vorläufigen Analyse der kryptologischen Schaltung I
wurde festgelegt, daß die in dieser Schaltung realisierte
Umformung der Eingangsfolge FUi (i=1,2,…) hinreichend
kompliziert ist (siehe [4]).
Deshalb konnte bei der Entwicklung der kryptologischen
Schaltung II am Prinzip der Erzeugung der Folge W, wie
es in der Schaltung I realisiert wird, festgehalten
werden: Erzeugung eines Elements wi von W im i-ten
Übertragungstakt durch n-malige rückgekoppelte Umformung
des Inhalts im Zustandsspeicher U des Chiffrators unter
Einwirkung des Abschnittes (fi,fi+1, …, fi+51) von F
und in Abhängigkeit vom Kurzzeitschlüssel S.
4. Festlegung der Grundstruktur der kryptologischen Schaltung II
Ausgehend von der Festlegung des Schlüsselsystems und
der Beibehaltung des Grundprinzips der Erzeugung der
Folge W wurde in Anlehnung an die Struktur der Schaltung I
für die kryptologische Schaltung II die in Abb. 3.3 dar-
gestellte Grundstruktur festgelegt.
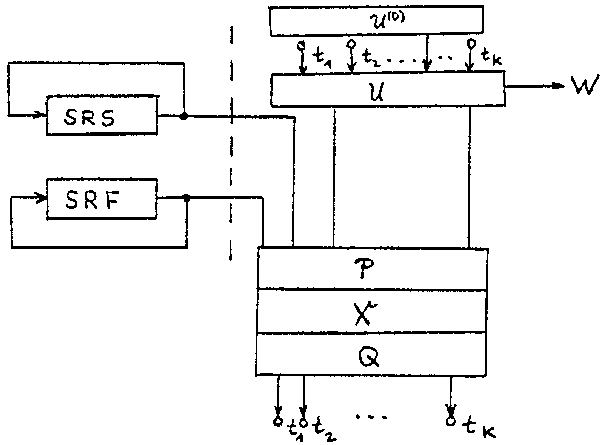
Abb. 3.3 Grundstruktur der kryptologischen Schaltung II
Im Speicher SRS ist der Kurzzeitschlüssel S gespeichert.
Die Kommutatoren P und Q und der Speicher U(0) für den
Anfangszustand U(0) des Chiffrators realisieren
den Langzeitschlüssel (P,Q,U(0)). SRF ist
Speicher des F-Generators. U ist der Zustandsspeicher
des Chiffrators, aus dem auch die Folge W abgeleitet wird.
X ist eine logische Funktion. Der Komplex (P,X,Q) rea-
lisiert die Überführungsfunktion ϕ:ExM→M
( -Zustandsmenge) des Chiffrators, E-Eingabemenge des
Chiffrators) des Chiffrators.
Bei der weiteren Präzisierung der Struktur des Chiffrators
mußte folgende Beschränkungen des Volumens des Chiffrators
beachtet werden:
Zur Realisierung des Chiffrators (U(0),P,Q,U,X) stand der
Platz für 10 Leiterplatten 170x94 mm zur Verfügung.
5. Festlegung der Parameter der kryptologischen Schaltung II
5.1 Anzahl der internen Arbeitstakte T 350 kHz pro Übertra-
gungstakt TÜi
Für die Entwicklung der kryptologischen Schaltung II wurde
eine Veränderung der Rekursion fi+52 = fi+3 ⊕ fi für
die Folge F=(fi)
-Zustandsmenge) des Chiffrators, E-Eingabemenge des
Chiffrators) des Chiffrators.
Bei der weiteren Präzisierung der Struktur des Chiffrators
mußte folgende Beschränkungen des Volumens des Chiffrators
beachtet werden:
Zur Realisierung des Chiffrators (U(0),P,Q,U,X) stand der
Platz für 10 Leiterplatten 170x94 mm zur Verfügung.
5. Festlegung der Parameter der kryptologischen Schaltung II
5.1 Anzahl der internen Arbeitstakte T 350 kHz pro Übertra-
gungstakt TÜi
Für die Entwicklung der kryptologischen Schaltung II wurde
eine Veränderung der Rekursion fi+52 = fi+3 ⊕ fi für
die Folge F=(fi) nicht als notwendig angesehen. Damit
bleibt die Begründung für die Wahl von 104 internen Ar-
beitstakten pro Übertragungstakt TÜi (i=1,2,…) die
gleiche wie in der Begründung der Schaltung I (s. [3], Punkt 5.2.3.1).
5.2 Kurzzeitschlüssel S
Entsprechend der Wahl von 104 internen Arbeitstakten pro
Übertragungstakt wurde die Länge der 0,1-Folge für den
Kurzzeitschlüssel S auf 104 Elemente bestimmt. Die Ver-
wendung nur einer Folge der Länge 104 als Kurzzeitschlüs-
sel wurde nicht als ausreichend eingeschätzt unter Beach-
tung des gegenwärtigen Standes de Analysearbeiten. Es
wird eingeschätzt, daß die Verwendung von zwei Folgen
S1, S2 mit je 104 Elementen als Kurzzeitschlüssel
S = (S1, S2) mit dem Schlüsselvorrat 2198
ausreicht.
5.3 Zustandsspeicher U
Die Größe des Zustandsspeichers U und seine Struktur haben
Einfluß auf die Kompliziertheit der durch den Chiffrator
realisierten kryptologischen Abbildung Bs mit
Bs(fi,fi+1, …, fi+51) = wi
(i=1,2,…;(fi, fi+1, …, fi+51) ∈ {0,1}52).
Der Zustandsspeicher U in der kryptologischen Schaltung I
hat 17 Speicherelemente. Durch Vergrößerung des Speichers
U wird bei entsprechender Gestaltung der Überführungsfunk-
tion ϕ die Abbildung Bs kryptologisch komplizierter.
Bei einer gewissen Einschränkung des technischen Aufwands
zur Realisierung der logischen Funktion X (s. Pkt. 5.4)
war es möglich, den Zustandsspeicher auf 27 Speicherele-
mente zu vergrößern und 9 Rückführungen t1,t2, …, t9 zu
realisieren (s. Abb. 3.4).
nicht als notwendig angesehen. Damit
bleibt die Begründung für die Wahl von 104 internen Ar-
beitstakten pro Übertragungstakt TÜi (i=1,2,…) die
gleiche wie in der Begründung der Schaltung I (s. [3], Punkt 5.2.3.1).
5.2 Kurzzeitschlüssel S
Entsprechend der Wahl von 104 internen Arbeitstakten pro
Übertragungstakt wurde die Länge der 0,1-Folge für den
Kurzzeitschlüssel S auf 104 Elemente bestimmt. Die Ver-
wendung nur einer Folge der Länge 104 als Kurzzeitschlüs-
sel wurde nicht als ausreichend eingeschätzt unter Beach-
tung des gegenwärtigen Standes de Analysearbeiten. Es
wird eingeschätzt, daß die Verwendung von zwei Folgen
S1, S2 mit je 104 Elementen als Kurzzeitschlüssel
S = (S1, S2) mit dem Schlüsselvorrat 2198
ausreicht.
5.3 Zustandsspeicher U
Die Größe des Zustandsspeichers U und seine Struktur haben
Einfluß auf die Kompliziertheit der durch den Chiffrator
realisierten kryptologischen Abbildung Bs mit
Bs(fi,fi+1, …, fi+51) = wi
(i=1,2,…;(fi, fi+1, …, fi+51) ∈ {0,1}52).
Der Zustandsspeicher U in der kryptologischen Schaltung I
hat 17 Speicherelemente. Durch Vergrößerung des Speichers
U wird bei entsprechender Gestaltung der Überführungsfunk-
tion ϕ die Abbildung Bs kryptologisch komplizierter.
Bei einer gewissen Einschränkung des technischen Aufwands
zur Realisierung der logischen Funktion X (s. Pkt. 5.4)
war es möglich, den Zustandsspeicher auf 27 Speicherele-
mente zu vergrößern und 9 Rückführungen t1,t2, …, t9 zu
realisieren (s. Abb. 3.4).
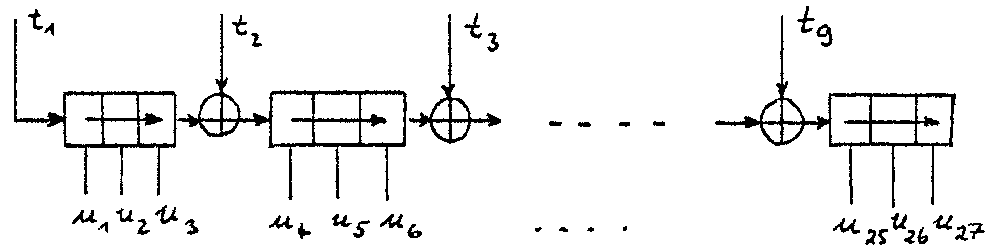
Abb. 3.4 Zustandsspeicher U
5.4 Die Realisierung der Überführungsfunktion ϕ
Ausgehend von der Struktur des Zustandsspeichers lag es
nahe, alle 27 Ausgänge von U an den Kommutator P zu führen
und permutiert in der logischen Funktion X zu verarbeiten.
Der Kommutator Q realisiert eine Permutation vom Grade 9.
Zur Realisierung von 9 unterschiedlichen Rückführungen
wurde in Anlehnung an die kryptologische Schaltung für
die logische Funktion X die in Abbildung 3.5 dargestellte
Struktur gewählt.
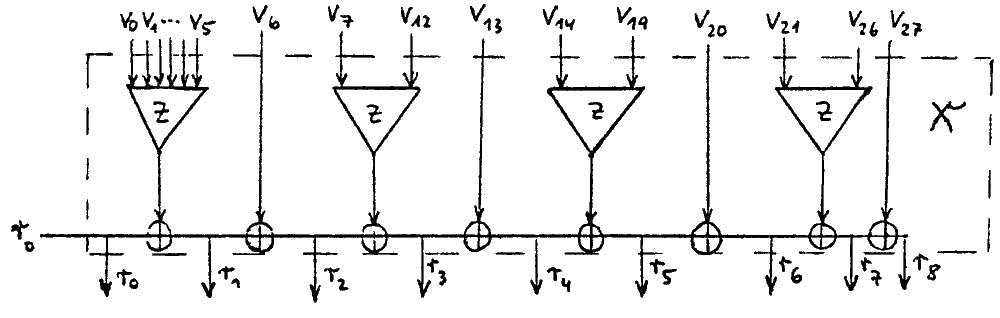
Abb. 3.5
Z: {0,1}6 → {0,1} ist eine logische
Funktion. In der Funktion der kryptologischen Schaltung I
wirken 6 logische Funktionen Z:{0,1}5 - {0,1}.
Die Beschränkung auf 4 logische Funktionen Z bedeutet
keine Verschlechterung, da die Anzahl der effektiv ver-
schiedenen Eingänge in X und die Anzahl der aus X abge-
leiteten Rückführungen wesentlich größer ist als in der
Schaltung I.
Durch die Festlegung von Z wird die kryptologische Qua-
lität des Chiffrators beeinflußt. Es wurde davon ausge-
gangen, daß eine Funktion Z kryptologisch geeignet ist,
wenn sie folgende Forderungen erfüllt:
(1) |{x = (x1,x2, …, x6) ∈ {0,1}6 | z(x) = 0}| = 25
(2) |{x = (x1,x2, …, x6) ∈ {0,1}6 | z(x) = 0,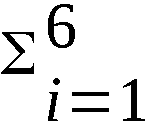 xi = r}|≈(
xi = r}|≈( )*1/2 (r = 0,1, …, 6)
(3) |{x = (x1,x2, …, x6) ∈ {0,1}6 | Z(x1, x2, …, xi, …, x6) = Z(x1, …, xi ⊕ 1, …, x6)} ≈ 25 (i = 1, 2,…, 6)
(4) Z ist nicht symmetrisch
(d. h., Z(x1,x2, …,x6) ≠ Z(xP1,xP2, …,xp6)
für eine beliebige Permutation P vom Grade 6, die ungleich
der identischen Abbildung ist.)
Das gewählte Z erfüllt diese Bedingungen.
Durch die Funktion X werden bei statistisch guten Eigen-
schaften der Eingangsfolgen statistisch gute Ausgangs-
folgen hergestellt.
5.5. Verarbeitung von FUi, S1 und S2
Zur Erhöhung der Kompliziertheit der durch den Chiffrator
realisierten Abbildungen Bs erscheint es günstig, FUi,
S1 und S2 in unterschiedlicher Weise im Chiffrator zu ver-
arbeiten. Die in der Abbildung 3.6 dargestellte Form der
Verarbeitung wurde für die erste Variante der kryptolo-
gischen Schaltung II (zur Konsultation im April in Moskau
vorgestellt, s. [5]) gewählt.
)*1/2 (r = 0,1, …, 6)
(3) |{x = (x1,x2, …, x6) ∈ {0,1}6 | Z(x1, x2, …, xi, …, x6) = Z(x1, …, xi ⊕ 1, …, x6)} ≈ 25 (i = 1, 2,…, 6)
(4) Z ist nicht symmetrisch
(d. h., Z(x1,x2, …,x6) ≠ Z(xP1,xP2, …,xp6)
für eine beliebige Permutation P vom Grade 6, die ungleich
der identischen Abbildung ist.)
Das gewählte Z erfüllt diese Bedingungen.
Durch die Funktion X werden bei statistisch guten Eigen-
schaften der Eingangsfolgen statistisch gute Ausgangs-
folgen hergestellt.
5.5. Verarbeitung von FUi, S1 und S2
Zur Erhöhung der Kompliziertheit der durch den Chiffrator
realisierten Abbildungen Bs erscheint es günstig, FUi,
S1 und S2 in unterschiedlicher Weise im Chiffrator zu ver-
arbeiten. Die in der Abbildung 3.6 dargestellte Form der
Verarbeitung wurde für die erste Variante der kryptolo-
gischen Schaltung II (zur Konsultation im April in Moskau
vorgestellt, s. [5]) gewählt.

Abb. 3.6
Die Elemente von FUi wirken unmittelbar über alle 9 Rück-
führungen t1,…,t9 auf den Speicher U. Der Einfluß von
FUi auf die Zustandsänderung des Chiffrators ist so be-
trachtet am stärksten on den drei Eingangskomponenten
FUi, S1, S2. Es wird angenommen, daß durch diese Verarbei-
tung von FUi die Zusammenhänge zwischen FUi und wi bzw.
zwischen F und W komplizierter werden als in der Schaltung I.
In ersten Untersuchungen zur Analyse der kryptologischen
Schaltung wurde festgestellt, daß die in Abb. 3.6 darge-
stellte Variante der Verarbeitung der Zeitschlüsselkom-
ponente S2 eine gewisse Einschränkung der Wirksamkeit von
S2 bedeutet. Für genau 226 der 227 möglichen Zustände U
des Chiffrators ist die Zustandsänderung U → U ϕ(u0,s,r)
unabhängig von s. Deshalb wurde festgelegt, S2 zusätzlich
noch zu w5 mod 2 zu addieren. Die Zustandsänderung
U → U ϕ(uo,s,r) ist dann für jedes Element U ∈{0,1}27 von
s abhängig. S2 wirkt immer entweder auf die Rückfüh-
rung r1,r2,r3,r5 oder r5,r6,r7,r8.
Im Laufe der technischen Entwicklung ergab sich noch die
Möglichkeit, S1 über den Kommutator Q (Erweiterung: Permu-
tation 10ten Grades) auf den Zustandsspeicher U einwirken
zu lassen. Diese Möglichkeit wurde genutzt.
5.6. Einstellung des Anfangszustandes U(0)
Durch die Rückstellung des Chiffrators in den Anfangszu-
stand U(0) jeweils nur zu Beginn der Erzeugung eines als
Additionsreihe genutzten Abschnittes (wi)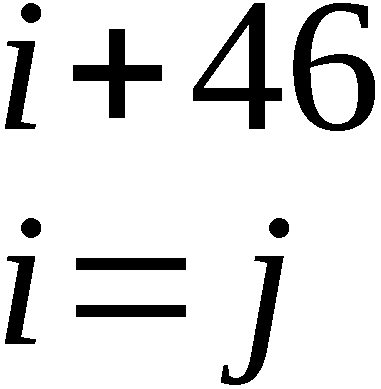 von W werden
alle Zusammenhänge zwischen (FUi)
von W werden
alle Zusammenhänge zwischen (FUi)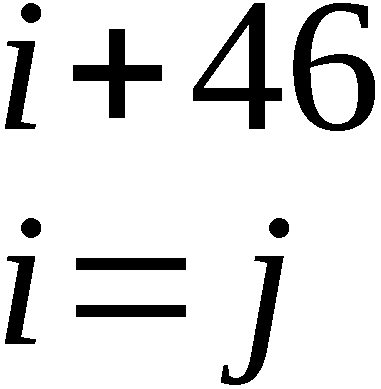 noch komplizierter
gestaltet.
Im Chiffrator werden unter dieser Voraussetzung 47 krypto-
logische Abbildungen
B
noch komplizierter
gestaltet.
Im Chiffrator werden unter dieser Voraussetzung 47 krypto-
logische Abbildungen
B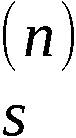 (n = 0, 1,…, 46) mit
B
(n = 0, 1,…, 46) mit
B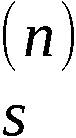 (fj, fj+1, …,fj+n+51) = wj+n
((fj, fj+1, …,fj+n+51) ∈ {0,1}n+52)
realisiert.
5.7 Abgriff der Elemente wi von W
Ursprünglich war vorgesehen, die Elemente wi von W nach
Ablauf der 104 internen Arbeitstakte pro Übertragungstakt
aus einem der Speicherelemente u1,u2,…,u27 von U zu
entnehmen. Das wurde kryptologisch als ausreichend einge-
schätzt.
Im Laufe der technischen Entwicklung der kryptologischen
Schaltung ergab sich die Möglichkeit, den Speicher U noch
um ein Speicherelement u28 zu erweitern und in der in
Abbildung 3.1 angegebenen Weise (Erweiterung der Relation
P: 28 Eingänge, 29 Ausgänge) einzusetzen.
§4 Kryptologische Sicherheit im System OPERATION
Die über das System OPERATION übermittelten Nachrichten werden
vor Kompromittierung gesichert durch den Kurzzeitschlüssel S
(Tagesschlüssel) unter der Voraussetzung, daß die Schlüs-
selherstellung qualitätsgerecht erfolgt und dem Gegner das
Chiffriersystem in allen Einzelheiten bekannt ist.
§5 Änderungsmöglichkeiten der kryptologischen Schaltung des
Chiffrators
1. Allgemeine Aussagen
(1) Änderungen der Schaltung einer Baugruppe sind i.a.
dann möglich, wenn sie nur eine Änderung der Ver-
drahtung zwischen den Leiterplatten der Baugruppen
erfordern.
(2) Änderungen einzelner Leiterplatten sind unter Schwie-
rigkeiten und i.a. nur dann möglich, wenn keine Aus-
wirkungen auf andere Leiterplatten auftreten und die
Anzahl der Leiterplatten in der Funktionseinheit
gleichbleibt.
2. Änderung der Struktur des Zustandsspeichers U
Der Zustandsspeicher U ist auf 4 Leiterplatten realisiert.
Auf jeder Leiterplatte sind 7 Speicherelemente in Gruppen
zu 3,2 und 2x1 Element und 5 Adder. Als Grundbausteine
für U stehen 4 Speicher der Länge 3, 4 Speicher der
Länge 2, 8 Speicher der Länge 1 und 10 Adder zur Verfügung.
Diese Grundbausteine können nach Wahl zusammengeschaltet
werden (Verdrahtungsänderung).
3. Änderung der Funktion X
Die Funktion Z wird auf einer Leiterplatte realisiert.
Diese Leiterplatte wird für das K5-Muster von Hand her-
gestellt. Die Funktion Z kann verändert werden unter der
Voraussetzung, daß die neue Funktion Z auf einer Leiter-
platte realisierbar ist.
Die Zusammenschaltung der 10 Adder die auf den Platinen
zur Realisierung von U noch übrig sind, zur Bildung der
r1,r2, …, r9 kann variiert werden (Verdrahtungsänderung).
4. Änderung der Festlegung des Anfangszustandes U(0)
Unter der Bedingung, daß der Kommutator Q nicht mehr
auf einer Leiterplatte sondern in der Verdrahtung des
Chiffrators realisiert wird und die freiwerdende Lei-
terplatte zusätzlich zur Steuerung der Anfangszustands-
einschaltung genutzt wird, kann der Anfangszustand U(0)
für den Chiffrator jeweils durch den Kurzzeitschlüssel
(S1, S2) bestimmt werden.
KAPITEL IV
Untersuchung der Struktur der Chiffrierabbildung
Einführung
Im vorliegenden Kapitel, das man unabhängig von den vorigen
lesen kann, werden die gewonnen Resultate der Untersuchung
der Struktur der Chiffrierabbildung des Chiffrators des Systems
OPERATION darlegt.
Die kryptologische Schaltung wird nicht in der allgemeinsten
Form untersucht, die im vorigen Kapitel beschrieben ist; die
genaue Definition des Gegenstandes der Untersuchungen werden
an den entsprechenden Stellen gegeben.
Wir geben im weiteren allgemeine und grundlegende Bezeichnun-
gen an, die im gesamten Kapitel verwendet werden. Mengen werden
entweder mit {…} oder mit großen deutschen Buchstaben
bezeichnet: F,
(fj, fj+1, …,fj+n+51) = wj+n
((fj, fj+1, …,fj+n+51) ∈ {0,1}n+52)
realisiert.
5.7 Abgriff der Elemente wi von W
Ursprünglich war vorgesehen, die Elemente wi von W nach
Ablauf der 104 internen Arbeitstakte pro Übertragungstakt
aus einem der Speicherelemente u1,u2,…,u27 von U zu
entnehmen. Das wurde kryptologisch als ausreichend einge-
schätzt.
Im Laufe der technischen Entwicklung der kryptologischen
Schaltung ergab sich die Möglichkeit, den Speicher U noch
um ein Speicherelement u28 zu erweitern und in der in
Abbildung 3.1 angegebenen Weise (Erweiterung der Relation
P: 28 Eingänge, 29 Ausgänge) einzusetzen.
§4 Kryptologische Sicherheit im System OPERATION
Die über das System OPERATION übermittelten Nachrichten werden
vor Kompromittierung gesichert durch den Kurzzeitschlüssel S
(Tagesschlüssel) unter der Voraussetzung, daß die Schlüs-
selherstellung qualitätsgerecht erfolgt und dem Gegner das
Chiffriersystem in allen Einzelheiten bekannt ist.
§5 Änderungsmöglichkeiten der kryptologischen Schaltung des
Chiffrators
1. Allgemeine Aussagen
(1) Änderungen der Schaltung einer Baugruppe sind i.a.
dann möglich, wenn sie nur eine Änderung der Ver-
drahtung zwischen den Leiterplatten der Baugruppen
erfordern.
(2) Änderungen einzelner Leiterplatten sind unter Schwie-
rigkeiten und i.a. nur dann möglich, wenn keine Aus-
wirkungen auf andere Leiterplatten auftreten und die
Anzahl der Leiterplatten in der Funktionseinheit
gleichbleibt.
2. Änderung der Struktur des Zustandsspeichers U
Der Zustandsspeicher U ist auf 4 Leiterplatten realisiert.
Auf jeder Leiterplatte sind 7 Speicherelemente in Gruppen
zu 3,2 und 2x1 Element und 5 Adder. Als Grundbausteine
für U stehen 4 Speicher der Länge 3, 4 Speicher der
Länge 2, 8 Speicher der Länge 1 und 10 Adder zur Verfügung.
Diese Grundbausteine können nach Wahl zusammengeschaltet
werden (Verdrahtungsänderung).
3. Änderung der Funktion X
Die Funktion Z wird auf einer Leiterplatte realisiert.
Diese Leiterplatte wird für das K5-Muster von Hand her-
gestellt. Die Funktion Z kann verändert werden unter der
Voraussetzung, daß die neue Funktion Z auf einer Leiter-
platte realisierbar ist.
Die Zusammenschaltung der 10 Adder die auf den Platinen
zur Realisierung von U noch übrig sind, zur Bildung der
r1,r2, …, r9 kann variiert werden (Verdrahtungsänderung).
4. Änderung der Festlegung des Anfangszustandes U(0)
Unter der Bedingung, daß der Kommutator Q nicht mehr
auf einer Leiterplatte sondern in der Verdrahtung des
Chiffrators realisiert wird und die freiwerdende Lei-
terplatte zusätzlich zur Steuerung der Anfangszustands-
einschaltung genutzt wird, kann der Anfangszustand U(0)
für den Chiffrator jeweils durch den Kurzzeitschlüssel
(S1, S2) bestimmt werden.
KAPITEL IV
Untersuchung der Struktur der Chiffrierabbildung
Einführung
Im vorliegenden Kapitel, das man unabhängig von den vorigen
lesen kann, werden die gewonnen Resultate der Untersuchung
der Struktur der Chiffrierabbildung des Chiffrators des Systems
OPERATION darlegt.
Die kryptologische Schaltung wird nicht in der allgemeinsten
Form untersucht, die im vorigen Kapitel beschrieben ist; die
genaue Definition des Gegenstandes der Untersuchungen werden
an den entsprechenden Stellen gegeben.
Wir geben im weiteren allgemeine und grundlegende Bezeichnun-
gen an, die im gesamten Kapitel verwendet werden. Mengen werden
entweder mit {…} oder mit großen deutschen Buchstaben
bezeichnet: F,  usw.
|{…}| - Zahl der Elemente der Menge {…}
{0,1}ɳ - Menge aller Tupel von Nullen und Einsen der
Länge n (|{0,1}ɳ)| = 2ɳ).
usw.
|{…}| - Zahl der Elemente der Menge {…}
{0,1}ɳ - Menge aller Tupel von Nullen und Einsen der
Länge n (|{0,1}ɳ)| = 2ɳ).
 = {0,1}27: wenn U= (Uα)
= {0,1}27: wenn U= (Uα) = (u1, u2, …, u27), dann
sei 2U = (u3ɳ-2)
= (u1, u2, …, u27), dann
sei 2U = (u3ɳ-2) , 1U = (u3ɳ-1)
, 1U = (u3ɳ-1) , 0U = (u3ɳ)
, 0U = (u3ɳ)
| P | = | ( | 1 | 2 | … | 27 | ) | , | | R | = | ( | 1 | 2 | … | 9 | ) | - Permutation; |
| P1 | P2 | … | P27 | R1 | R2 | … | R9 |
{(P,R)} - Menge aller möglichen Permutationspaare (P,R);
| P0 | = | ( | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | ) |
| 22 | 7 | 18 | 2 | 16 | 27 | 23 | 3 | 14 | 1 | 13 | 25 | 24 | 12 | 17 | 4 | 11 | 9 | 26 | 15 | 10 | 19 | 8 | 5 | 20 | 6 | 21 |
| R0 | = | ( | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ). |
| 8 | 5 | 6 | 2 | 9 | 4 | 7 | 3 | 1 |
Z -logische Funktion (Boolsche Funktion):
Z = Z (e1,e2,…,e6) = Z(1,2,…,6) =
L+1+5+6+14+23+25+45+56+134+136+145+236+246+
356+1234+1235+1256+2346+12345+13456
(Addition mod 2; diese Art der Addition wird hier und im
weiteren nicht speziell erwähnt, weil sie immer eindeutig
aus dem Kontext bestimmt wird);
___
logische Funktionen Tɳ = Tɳ (e2,e2,…,e28), ɳ = 1,9:
TR1 = 0
TR2 = Z(e1,e2,…,e6)
TR3 = TR2 + e7
TR4 = TR3 + Z(e8,e9,…,e13)
TR5 = TR4 + e14
TR6 = TR5 + Z(e15,e16,…,e20)
TR7 = TR6 + e21
TR8 = TR7 + Z(e22,e23,…,e27)
TR9 = TR8 + e28.
§1 Die Abbildung ϕ
1. Definition der Abbildung ϕ
Ausgangspunkt der kryptologischen Untersuchungen des Chif-
frators des Systems OPERATION sind die Eigenschaften der
Umformung des xx-Registerinhalts. Deshalb beschäftigen wir
uns zuerst mit dieser Frage und damit zusammenhängenden
Problemen.
Seien U = (u1,u2,…,u27) ∈  ;
Y = (y1,y2,…,y27) ∈
;
Y = (y1,y2,…,y27) ∈  ;
u0 ∈{0,1}, s ∈{0,1}, r ∈{0,1} - Parameter;
∆ɳ,ɳ = 1,9 - Konstante: ∆ɳ =
;
u0 ∈{0,1}, s ∈{0,1}, r ∈{0,1} - Parameter;
∆ɳ,ɳ = 1,9 - Konstante: ∆ɳ = 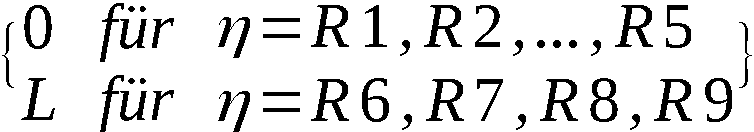 Die Abbildung ϕ = ϕ(u0,s,r) der Menge
Die Abbildung ϕ = ϕ(u0,s,r) der Menge  in sich, die
U ∈
in sich, die
U ∈  auf ϕU = Y ∈
auf ϕU = Y ∈  abbildet, bestimmt sich aus den
Formeln
y3n-1 = u3n-3 + r+ s∆ɳ + Tɳ(S,uP1,uP2,…,uP27) |
y3n-1 = u3n-2 > (1.1)
y3n = u3n-1, n = 1,9 |
Wir bezeichnen mit {ϕnU} die Menge aller Elemente von
abbildet, bestimmt sich aus den
Formeln
y3n-1 = u3n-3 + r+ s∆ɳ + Tɳ(S,uP1,uP2,…,uP27) |
y3n-1 = u3n-2 > (1.1)
y3n = u3n-1, n = 1,9 |
Wir bezeichnen mit {ϕnU} die Menge aller Elemente von  ,
die man aus U nach genau n Schritten erhält (n-fache Anwen-
dung von ϕ), n sei eine natürliche Zahl, die Parameter
können alle möglichen Werte annehmen.
2. Bedingungen für die Eineindeutigkeit von ϕ
2.1. Das grundlegende Gleichungssystem
Unter kryptologischen Gesichtspunkten spielt die Menge PR
aller der Permutationspaaren (P,R) ∈ {(P,R)} eine ent-
scheidende Rolle, für die die Abbildung ϕ bei beliebigen
Parameterwerten (u0,s,r) eineindeutig ist, d.h. eine Abbil-
dung der Menge
,
die man aus U nach genau n Schritten erhält (n-fache Anwen-
dung von ϕ), n sei eine natürliche Zahl, die Parameter
können alle möglichen Werte annehmen.
2. Bedingungen für die Eineindeutigkeit von ϕ
2.1. Das grundlegende Gleichungssystem
Unter kryptologischen Gesichtspunkten spielt die Menge PR
aller der Permutationspaaren (P,R) ∈ {(P,R)} eine ent-
scheidende Rolle, für die die Abbildung ϕ bei beliebigen
Parameterwerten (u0,s,r) eineindeutig ist, d.h. eine Abbil-
dung der Menge  auf sich ist: ϕ
auf sich ist: ϕ =
=  .
Wenden wir uns der Bestimmung von (P,R) ∈ PR zu.
Bemerkung: Die Klasse PR und die Methode ihrer Bestimmung
sind dieselben, wenn man annimmt
∆ɳ = 0 für alle ɳ = 1,9
Die Forderung (P,R) ∈ PR ist gleichbedeutend damit, daß für
alle Y ∈
.
Wenden wir uns der Bestimmung von (P,R) ∈ PR zu.
Bemerkung: Die Klasse PR und die Methode ihrer Bestimmung
sind dieselben, wenn man annimmt
∆ɳ = 0 für alle ɳ = 1,9
Die Forderung (P,R) ∈ PR ist gleichbedeutend damit, daß für
alle Y ∈  und (u0,s,r) ∈{0,1}3 das System (1.1) eine
eindeutige Lösung U = (u1,u2,…u27) ∈
und (u0,s,r) ∈{0,1}3 das System (1.1) eine
eindeutige Lösung U = (u1,u2,…u27) ∈  hat.
Offensichtlich sind wegen
u3ɳ-2 = y3ɳ-1, u3ɳ-1 =y3ɳ (n=1,9)
Unbekannt nur die 9 Werte u3ɳ, ɳ = 1,9.
Wir bezeichnen
(2.1)
u27 = x9
u3Rɳ-3 = xɳ-1, ɳ = 1,9
y3Rɳ-2 + y3R(ɳ-1) = hɳ, ɳ=2,9
y3R1-2 + r = h1
Dann kann man durch paarweise Addition der ersten 9
Gleichungen des Systems (1.1) zu folgender Formel
gelangen:
(2.2)
(1) 0 = x0 + h1
(2) 0 = x1 + x0 + Z(s,uP1,…,uP5) + h2
(3) 0 = x2 + x1 + uP6 + h3
(4) 0 = x3 + x2 + Z(uP7,…,uP12) + h4
(5) 0 = x4 + x3 + uP13 + h5
(6) 0 = x5 + x4 + Z(uP14,…,uP19) + s + h6
(7) 0 = x6 + x5 + uP20 + h7
(8) 0 = x7 + x6 + Z(uP21,…,uP26) + h8
(9) 0 = x8 + x7 + uP27 + h9
(10) 0 = U0 + xR1-1
Dieses System soll eine eindeutige Lösung für alle Parameter-
werte habe, wenn man x0,x1,…x9 als Unbekannte annimmt,
und h1,h2,…,h9,u0,s,u1,u2,u4,u5,u7,…u26 als
Parameter, die unabhängig voneinander jeden beliebigen Wert
0 oder 1 annehmen können.
Wir bezeichnen das System (2.2) als grundlegendes Gleichungs-
system, da es eine entscheidende Rolle bei der Klärung der
Eigenschaften der Abbildung ϕ spielt.
2.2 Notwendige Bedingungen
Wir finden einige notwendige Bedingungen dafür, daß
(P,R) ∈ PR erfüllt ist.
(N1) R1 ≠ 1
Für R1 = 1 gilt gleichzeitig x0 = h1 und x0 = u0, dies ist
aber nicht zulässig.
(N2) P27 ≠ 3R9-3
Beweis: Wenn P27 = 3R9-3, so gilt infolge (2.1) UP27 = x8.
Da in diesem Fall x8 in keiner anderen Gleichung
vorkommt, muß es aus der Gleichung uP27 = x8 be-
stimmt werden. Das heißt, uP27 muß einer der Parame-
ter u1,u2,u4,u5,u7,…,u26 sein. Aber dies ist
unmöglich, da nach Voraussetzung P27 ≡ 0 (mod 3) gilt.
(N3) Bei R2 = 1 muß gelten P6 ≠ 3R3-3
Beweis: R2 = 1 ~>(10) x1 = u0 |
> ~>(3) u0 + h3 = 0
P6 = 3R3-3 ~>(2.1) x2 = up6 | s1 = h3
(N4) Bei R3 = 1 muß gelten P6 ≠ 3R2-3
(N5) Bei R4 = 1 muß gelten P13 ≠ 3R5-3
(N6) Bei R5 = 1 muß gelten P13 ≠ 3R4-3
(N7) Bei R6 = 1 muß gelten P20 ≠ 3R7-3
(N8) Bei R7 = 1 muß gelten P20 ≠ 3R6-3
(N9) Bei R9 = 1 muß gelten P27 ≠ 3R8-3
(N4) bis (N9) werden analog (N3) bewiesen.
2.3 Hinreichende Bedingungen
Am Beispiel zweigen wir, wie man Untermengen der Menge PR
erhalten kann, wenn man von dem grundlegenden Gleichungs-
system (2.2) ausgeht.
Die Methode besteht in der sukzessiven Bestimmung der
Unbekannten x0,x1,…,x9.
Jede Gleichung dient der Bestimmung genau einer Unbekannten.
Dabei wird stufenweise ein System hinreichender Bedingungen
dafür erarbeitet, daß (P,R) ∈ PR ist.
Schritt 1 : (1) → x0 = h1
Schritt 2 : Sei R4 = 1, dann: (10) → x3 = u0
Schritt 3 : Sei τ1,τ2,…,τ5 irgend eine Permutation
der Zahlen 1,2,…,5, symbolisch:{τ1,…,τ5} = {1,…,5};
Pτ2,Pτ3Pτ4,Pτ5 ≠ 0 (mod 3); Pτ1 = 3R1-3.
Dann ist uPτ1 = x0 = h1, folglich enthält
Z(s,uP1,…,up5) keine Unbekannte,
folglich: (2) → x1 = h1 + h2 + Z.
Schritt 4 : Sei {τ7,…,τ12} = {7,…,12};
Pτ7 = 3R2-3; Pτ8,…,Pτ12 ≠ 0 (mod 3).
Dann folgt analog uPτ7 = x1 und
(4) → x2 = u0 + h4 + Z.
Schritt 5 : Sei P6 = 3R5-3. Dann ist up6 = x4, und
(3) → x4 = x1 + xx2 + h3.
Schritt 6 : Sei {τ14,…,τ19} = {14,…19};
Pτ14 = 3R3-3; Pτ15,…,Pτ19 ≠ 0 (mod 3).
Dann ist UPτ14 = x2 und
(6) → x5 = x4 + Z + S + h6.
Schritt 7 : Sei P13 = 3R7-3. Dann ist UP13 = x6, und
(5) → x6 = x3 + x4 + h5.
Schritt 8 : Sei P27 = 3R8-3. Dann ist UP27 = x7, und
(9) → x8 = h9.
Schritt 9 : Sei P20 = 27. Dann ist uP20 = x9, und
(7) → x9 = x5 + x6 + h7.
Schritt 10: Sei {τ21,…,τ26} = {21,…,26};
Pτ21 = 3R6-3; Pτ22 = 3R9-3; Pτ23,…,Pτ26 ≠ 0 (mod 3).
Dann ist uPτ21 = x5, uPτ22 = x8 und
(8) → x7 = x6 + Z + h8.
Alle Gleichungen sind also verwertet und die Unbekannten sind
gefunden. Widersprüche sind nicht aufgetreten.
Zusammenfassend kann man folgende hinreichende Bedingungen
dafür, daß (P,R) ∈ PR erfüllt ist, formulieren.
(D 1) Es gelten gleichzeitig die Gleichungen
R4 = 1, P20 = 27, P6 = 3R5-3, P13 = 3R7-3,
P27 = 3R8-3, Pτ1 = 3R1-3, Pτ7 = 3R2-3,
Pτ21 = 3R6-3, Pτ22 = 3R9-3, Pτ14 = 3R3-3
wobei
τ1 ∈{1,…,5}, τ7 ∈{7,…,12}, τ14 ∈{14,…,19},
τ21 ∈{21,…,26}, τ22 ∈{21,…,26}, τ21 ≠ τ22
Völlig analog lassen sich folgende hinreichende Bedingungen
herleiten:
(D 2) Es gelten gleichzeitig die Gleichungen
R3 = 1, P6 = 27, Pτ7 = 3R1-3, Pτ1 = 3R2-3,
Pτ21 = 3R4-3, Pτ15 = 3R5-3, P20 = 3R6-3,
Pτ22 = 3R7-3, Pτ16 = 3R8-3, Pτ17 = 3R9-3
wobei
τ7 ∈{7,…,12}, τ21, τ22 ∈{21,…,26}
τ14, τ15, τ16, τ17, ∈{14,…,19}
und alle τ seinen paarweise verschieden.
(D 3) Es gelten gleichzeitig die Gleichungen
R5 = 1, P6 = 27, Pτ7 = 3R1-3, Pτ8 = 3R6-3,
Pτ9 = 3R9-3, Pτ14 = 3R4-3, Pτ21 = 3R2-3,
Pτ22 = 3R3-3, Pτ23 = 3R7-3, P27 = 3R8-3
wobei
τ7, τ8, τ9 ∈{7,…,12},
τ14 ∈ {14,…,19},
τ21, τ22, τ23 ∈ {21,…,26}
und alle τ seien paarweise verschieden.
(D 4) Es gelten gleichzeitig die Gleichungen
R6 = 1, P6 = 27, Pτ7 = 3R5-3, Pτ8 = 3R9-3,
Pτ14 = 3R1-3, Pτ15 = 3R2-3, Pτ21 = 3R3-3,
Pτ22 = 3R4-3, Pτ23 = 3R7-3, P27 = 3R8-3
wobei
τ7, τ8 ∈ {7,…,12},
τ14, τ15 ∈ {14,…,19},
τ21, τ22, τ23 ∈ {21,…,26}
und alle τ seien paarweise verschieden.
(D 5) Es gelten gleichzeitig die Gleichungen
R7 = 1, Pτr = 3R8-3, Pτ7 = 3R9-3, Pτ8 = 3R2-3,
Pτ9 = 3R3-3, P13 = 3R4-3, Pτ14 = 3R5-3,
P20 = 27, Pτ21 = 3R1-3, Pτ22 = 3R6-3
wobei
τ1 ∈ {1,…,5},
τ7, τ8, τ9 ∈ {7,…,12}, τ14 ∈ {14,…,19}
τ21, τ22 ∈{21,…,26}
und alle τ seien paarweise verschieden.
(D 6) Es gelten gleichzeitig die Gleichungen
R8 = 1, Pτ1 = 3R7-3, Pτ7 = 3R2-3, P27 = 27,
Pτ8 = 3R3-3, P13 = 3R4-3, Pτ14 = 3R1-3,
Pτ15 = 3R5-3, P20 = 3R9-3, Pτ21 = 3R6-3
wobei
τ1 ∈ {1,…,5},
τ14, τ15 ∈ {14,…,19},
τ21 ∈{21,…,26}
und alle τ seien paarweise verschieden.
(D 7) Es gelten gleichzeitig die Gleichungen
R9 = 1, P13 = 3R4-3, P27 = 27,
Pτ1 = 3R1-3, Pτ2 = 3R2-3,
Pτ8 = 3R3-3, Pτ9 = 3R8-3, Pτ14 = 3R5-3,
Pτ21 = 3R6-3
wobei
τ1, τ2 ∈ {1,…,5},
τ7, τ8, τ9 ∈ {7,…,12},
τ14 ∈{14,…,19}, τ21 ∈{21,…,26}
und alle τ seien paarweise verschieden.
(D 8)
R9 = 1, P6 = 27, P27 = 3R1-3, P20 = 3R3-3,
Pτ7 = 3R4-3, P13 = 3R5-3, Pτ14 = 3R2-3
Pτ15 = 3R6-3, Pτ1 = 3R7-3, Pτ21 = 3R8-3,
wobei
τ1 ∈ {1,…,5}, , τ7 ∈ {7,…,12}
τ14, τ15 ∈{14,…,19}, τ21 ∈{21,…,26}, τ14 ≠ τ15.
2.4 Die Anzahl der Elemente in PR
Aus den erhaltenen Ergebnissen kann man für |PR| die Ab-
schätzung
(2.3)
1026 < |PR| < 1034
herleiten.
Beweis:
(1) Offensichtlich gilt |{PR}| = 27! * 9!.
Der Bedingung R1 = 1 genügen 27! * 8! Paare, und
der Bedingung P27 = 3R9 - 3 genügen 26! * 9! Paare.
Deshalb gilt
|PR| ≤ 27! * 9! - 27! * 8! - 26! * 9! + 26! * 8! =
26! * 8! * 26 * 8 ≈ 3*1033.
(2) Wir betrachten (D1).
Wegen
{R5,R7,R8,R1,R2,R6,R9,R3} = {2,3,4,5,6,7,8,9}
muß
{P6,P13,P27,Pτ1,Pτ7,Pτ21,Pτ22,Pτ14} = {3,6,9,12,15,18,21,24}
sein.
Das ergibt den Faktor
8! + 5 * 6 * 6 *
hat.
Offensichtlich sind wegen
u3ɳ-2 = y3ɳ-1, u3ɳ-1 =y3ɳ (n=1,9)
Unbekannt nur die 9 Werte u3ɳ, ɳ = 1,9.
Wir bezeichnen
(2.1)
u27 = x9
u3Rɳ-3 = xɳ-1, ɳ = 1,9
y3Rɳ-2 + y3R(ɳ-1) = hɳ, ɳ=2,9
y3R1-2 + r = h1
Dann kann man durch paarweise Addition der ersten 9
Gleichungen des Systems (1.1) zu folgender Formel
gelangen:
(2.2)
(1) 0 = x0 + h1
(2) 0 = x1 + x0 + Z(s,uP1,…,uP5) + h2
(3) 0 = x2 + x1 + uP6 + h3
(4) 0 = x3 + x2 + Z(uP7,…,uP12) + h4
(5) 0 = x4 + x3 + uP13 + h5
(6) 0 = x5 + x4 + Z(uP14,…,uP19) + s + h6
(7) 0 = x6 + x5 + uP20 + h7
(8) 0 = x7 + x6 + Z(uP21,…,uP26) + h8
(9) 0 = x8 + x7 + uP27 + h9
(10) 0 = U0 + xR1-1
Dieses System soll eine eindeutige Lösung für alle Parameter-
werte habe, wenn man x0,x1,…x9 als Unbekannte annimmt,
und h1,h2,…,h9,u0,s,u1,u2,u4,u5,u7,…u26 als
Parameter, die unabhängig voneinander jeden beliebigen Wert
0 oder 1 annehmen können.
Wir bezeichnen das System (2.2) als grundlegendes Gleichungs-
system, da es eine entscheidende Rolle bei der Klärung der
Eigenschaften der Abbildung ϕ spielt.
2.2 Notwendige Bedingungen
Wir finden einige notwendige Bedingungen dafür, daß
(P,R) ∈ PR erfüllt ist.
(N1) R1 ≠ 1
Für R1 = 1 gilt gleichzeitig x0 = h1 und x0 = u0, dies ist
aber nicht zulässig.
(N2) P27 ≠ 3R9-3
Beweis: Wenn P27 = 3R9-3, so gilt infolge (2.1) UP27 = x8.
Da in diesem Fall x8 in keiner anderen Gleichung
vorkommt, muß es aus der Gleichung uP27 = x8 be-
stimmt werden. Das heißt, uP27 muß einer der Parame-
ter u1,u2,u4,u5,u7,…,u26 sein. Aber dies ist
unmöglich, da nach Voraussetzung P27 ≡ 0 (mod 3) gilt.
(N3) Bei R2 = 1 muß gelten P6 ≠ 3R3-3
Beweis: R2 = 1 ~>(10) x1 = u0 |
> ~>(3) u0 + h3 = 0
P6 = 3R3-3 ~>(2.1) x2 = up6 | s1 = h3
(N4) Bei R3 = 1 muß gelten P6 ≠ 3R2-3
(N5) Bei R4 = 1 muß gelten P13 ≠ 3R5-3
(N6) Bei R5 = 1 muß gelten P13 ≠ 3R4-3
(N7) Bei R6 = 1 muß gelten P20 ≠ 3R7-3
(N8) Bei R7 = 1 muß gelten P20 ≠ 3R6-3
(N9) Bei R9 = 1 muß gelten P27 ≠ 3R8-3
(N4) bis (N9) werden analog (N3) bewiesen.
2.3 Hinreichende Bedingungen
Am Beispiel zweigen wir, wie man Untermengen der Menge PR
erhalten kann, wenn man von dem grundlegenden Gleichungs-
system (2.2) ausgeht.
Die Methode besteht in der sukzessiven Bestimmung der
Unbekannten x0,x1,…,x9.
Jede Gleichung dient der Bestimmung genau einer Unbekannten.
Dabei wird stufenweise ein System hinreichender Bedingungen
dafür erarbeitet, daß (P,R) ∈ PR ist.
Schritt 1 : (1) → x0 = h1
Schritt 2 : Sei R4 = 1, dann: (10) → x3 = u0
Schritt 3 : Sei τ1,τ2,…,τ5 irgend eine Permutation
der Zahlen 1,2,…,5, symbolisch:{τ1,…,τ5} = {1,…,5};
Pτ2,Pτ3Pτ4,Pτ5 ≠ 0 (mod 3); Pτ1 = 3R1-3.
Dann ist uPτ1 = x0 = h1, folglich enthält
Z(s,uP1,…,up5) keine Unbekannte,
folglich: (2) → x1 = h1 + h2 + Z.
Schritt 4 : Sei {τ7,…,τ12} = {7,…,12};
Pτ7 = 3R2-3; Pτ8,…,Pτ12 ≠ 0 (mod 3).
Dann folgt analog uPτ7 = x1 und
(4) → x2 = u0 + h4 + Z.
Schritt 5 : Sei P6 = 3R5-3. Dann ist up6 = x4, und
(3) → x4 = x1 + xx2 + h3.
Schritt 6 : Sei {τ14,…,τ19} = {14,…19};
Pτ14 = 3R3-3; Pτ15,…,Pτ19 ≠ 0 (mod 3).
Dann ist UPτ14 = x2 und
(6) → x5 = x4 + Z + S + h6.
Schritt 7 : Sei P13 = 3R7-3. Dann ist UP13 = x6, und
(5) → x6 = x3 + x4 + h5.
Schritt 8 : Sei P27 = 3R8-3. Dann ist UP27 = x7, und
(9) → x8 = h9.
Schritt 9 : Sei P20 = 27. Dann ist uP20 = x9, und
(7) → x9 = x5 + x6 + h7.
Schritt 10: Sei {τ21,…,τ26} = {21,…,26};
Pτ21 = 3R6-3; Pτ22 = 3R9-3; Pτ23,…,Pτ26 ≠ 0 (mod 3).
Dann ist uPτ21 = x5, uPτ22 = x8 und
(8) → x7 = x6 + Z + h8.
Alle Gleichungen sind also verwertet und die Unbekannten sind
gefunden. Widersprüche sind nicht aufgetreten.
Zusammenfassend kann man folgende hinreichende Bedingungen
dafür, daß (P,R) ∈ PR erfüllt ist, formulieren.
(D 1) Es gelten gleichzeitig die Gleichungen
R4 = 1, P20 = 27, P6 = 3R5-3, P13 = 3R7-3,
P27 = 3R8-3, Pτ1 = 3R1-3, Pτ7 = 3R2-3,
Pτ21 = 3R6-3, Pτ22 = 3R9-3, Pτ14 = 3R3-3
wobei
τ1 ∈{1,…,5}, τ7 ∈{7,…,12}, τ14 ∈{14,…,19},
τ21 ∈{21,…,26}, τ22 ∈{21,…,26}, τ21 ≠ τ22
Völlig analog lassen sich folgende hinreichende Bedingungen
herleiten:
(D 2) Es gelten gleichzeitig die Gleichungen
R3 = 1, P6 = 27, Pτ7 = 3R1-3, Pτ1 = 3R2-3,
Pτ21 = 3R4-3, Pτ15 = 3R5-3, P20 = 3R6-3,
Pτ22 = 3R7-3, Pτ16 = 3R8-3, Pτ17 = 3R9-3
wobei
τ7 ∈{7,…,12}, τ21, τ22 ∈{21,…,26}
τ14, τ15, τ16, τ17, ∈{14,…,19}
und alle τ seinen paarweise verschieden.
(D 3) Es gelten gleichzeitig die Gleichungen
R5 = 1, P6 = 27, Pτ7 = 3R1-3, Pτ8 = 3R6-3,
Pτ9 = 3R9-3, Pτ14 = 3R4-3, Pτ21 = 3R2-3,
Pτ22 = 3R3-3, Pτ23 = 3R7-3, P27 = 3R8-3
wobei
τ7, τ8, τ9 ∈{7,…,12},
τ14 ∈ {14,…,19},
τ21, τ22, τ23 ∈ {21,…,26}
und alle τ seien paarweise verschieden.
(D 4) Es gelten gleichzeitig die Gleichungen
R6 = 1, P6 = 27, Pτ7 = 3R5-3, Pτ8 = 3R9-3,
Pτ14 = 3R1-3, Pτ15 = 3R2-3, Pτ21 = 3R3-3,
Pτ22 = 3R4-3, Pτ23 = 3R7-3, P27 = 3R8-3
wobei
τ7, τ8 ∈ {7,…,12},
τ14, τ15 ∈ {14,…,19},
τ21, τ22, τ23 ∈ {21,…,26}
und alle τ seien paarweise verschieden.
(D 5) Es gelten gleichzeitig die Gleichungen
R7 = 1, Pτr = 3R8-3, Pτ7 = 3R9-3, Pτ8 = 3R2-3,
Pτ9 = 3R3-3, P13 = 3R4-3, Pτ14 = 3R5-3,
P20 = 27, Pτ21 = 3R1-3, Pτ22 = 3R6-3
wobei
τ1 ∈ {1,…,5},
τ7, τ8, τ9 ∈ {7,…,12}, τ14 ∈ {14,…,19}
τ21, τ22 ∈{21,…,26}
und alle τ seien paarweise verschieden.
(D 6) Es gelten gleichzeitig die Gleichungen
R8 = 1, Pτ1 = 3R7-3, Pτ7 = 3R2-3, P27 = 27,
Pτ8 = 3R3-3, P13 = 3R4-3, Pτ14 = 3R1-3,
Pτ15 = 3R5-3, P20 = 3R9-3, Pτ21 = 3R6-3
wobei
τ1 ∈ {1,…,5},
τ14, τ15 ∈ {14,…,19},
τ21 ∈{21,…,26}
und alle τ seien paarweise verschieden.
(D 7) Es gelten gleichzeitig die Gleichungen
R9 = 1, P13 = 3R4-3, P27 = 27,
Pτ1 = 3R1-3, Pτ2 = 3R2-3,
Pτ8 = 3R3-3, Pτ9 = 3R8-3, Pτ14 = 3R5-3,
Pτ21 = 3R6-3
wobei
τ1, τ2 ∈ {1,…,5},
τ7, τ8, τ9 ∈ {7,…,12},
τ14 ∈{14,…,19}, τ21 ∈{21,…,26}
und alle τ seien paarweise verschieden.
(D 8)
R9 = 1, P6 = 27, P27 = 3R1-3, P20 = 3R3-3,
Pτ7 = 3R4-3, P13 = 3R5-3, Pτ14 = 3R2-3
Pτ15 = 3R6-3, Pτ1 = 3R7-3, Pτ21 = 3R8-3,
wobei
τ1 ∈ {1,…,5}, , τ7 ∈ {7,…,12}
τ14, τ15 ∈{14,…,19}, τ21 ∈{21,…,26}, τ14 ≠ τ15.
2.4 Die Anzahl der Elemente in PR
Aus den erhaltenen Ergebnissen kann man für |PR| die Ab-
schätzung
(2.3)
1026 < |PR| < 1034
herleiten.
Beweis:
(1) Offensichtlich gilt |{PR}| = 27! * 9!.
Der Bedingung R1 = 1 genügen 27! * 8! Paare, und
der Bedingung P27 = 3R9 - 3 genügen 26! * 9! Paare.
Deshalb gilt
|PR| ≤ 27! * 9! - 27! * 8! - 26! * 9! + 26! * 8! =
26! * 8! * 26 * 8 ≈ 3*1033.
(2) Wir betrachten (D1).
Wegen
{R5,R7,R8,R1,R2,R6,R9,R3} = {2,3,4,5,6,7,8,9}
muß
{P6,P13,P27,Pτ1,Pτ7,Pτ21,Pτ22,Pτ14} = {3,6,9,12,15,18,21,24}
sein.
Das ergibt den Faktor
8! + 5 * 6 * 6 *  * 2! = 8! * 5400.
Es sind 18 Elemente von P beliebig.
Deshalb gilt
(D1)
genügen 18! * 8! * 5400 Paare (P,R).
Analog läßt sich errechnen daß
(D2)
18! * 8! * 6 + (6 2) *
* 2! = 8! * 5400.
Es sind 18 Elemente von P beliebig.
Deshalb gilt
(D1)
genügen 18! * 8! * 5400 Paare (P,R).
Analog läßt sich errechnen daß
(D2)
18! * 8! * 6 + (6 2) *  *2! * 4! Paare entsprechen,
(D3)
genügen 18! * 8! * 6 *
*2! * 4! Paare entsprechen,
(D3)
genügen 18! * 8! * 6 * 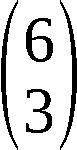 *
*  * 3! * 3! Paare,
(D4)
genügen 18! * 8! * 6 *
* 3! * 3! Paare,
(D4)
genügen 18! * 8! * 6 *  *
*  * (6 3) * 2! * 2! * 3! Paare,
(D5)
genügen 18! * 8! * 5 * 6 *
* (6 3) * 2! * 2! * 3! Paare,
(D5)
genügen 18! * 8! * 5 * 6 * 
 * 2! * 3! Paare,
(D6)
genügen 18! * 8! * 5 * 6 *
* 2! * 3! Paare,
(D6)
genügen 18! * 8! * 5 * 6 * 
 * 2! * 2! Paare,
(D7)
genügen 18! * 8! * 6 * 6 *
* 2! * 2! Paare,
(D7)
genügen 18! * 8! * 6 * 6 * 
 * 2! * 3! Paare,
(D8)
genügen 18! * 8! * 6 * 6 *
* 2! * 3! Paare,
(D8)
genügen 18! * 8! * 6 * 6 *  * 2! Paare.
Summiert man alle diese Zahlen auf, so erhält man
|PR| ≥ 18! * 8! * 52 * 63 *91 ≈ 1,3 * 1026.
3. Fixpunkte
3.1 Als Fixpunkte der Abbildung ϕ wird ein solches Element
U ∈
* 2! Paare.
Summiert man alle diese Zahlen auf, so erhält man
|PR| ≥ 18! * 8! * 52 * 63 *91 ≈ 1,3 * 1026.
3. Fixpunkte
3.1 Als Fixpunkte der Abbildung ϕ wird ein solches Element
U ∈  bezeichnet, für welches
ϕU = U
für irgendeinen Parameterwert (u0,s,r) gilt.
Für Fixpunkte U hat das System (1.1) das Aussehen
(3.1)
U3ɳ-2 = U3ɳ-3 + r + s∆ɳ Tɳ(s,Up)
U3ɳ-1 = U3ɳ-2
U3ɳ = U3ɳ-1, n = 1,9.
Daraus ergeben sich notwendige Bedingungen für Fixpunkte:
(N1) U3ɳ-2 = U3ɳ-1 = U3ɳ, ɳ = 1,9
(N2) U3R1-2 + U3R1-3 + r = 0 (wegen ∆R1 = TR1 = 0)
Um für konkrete (P,R) und (u0,s,r) Fixpunkte zu finden, muß
das System (3.1) bezüglich der Unbekannten u1,u2,…,u27
gelöst werden, was keine prinzipiellen Schwierigkeiten
bereitet.
Für (P0,R0) werden alle Fixpunkte errechnet:
u0 s r u3 u6 u9 u12 u15 u18 u21 u24 u27
0 0 0 0 0 1 0 0 0 1 1 0
0 0 1 0 1 1 1 0 0 0 1 1
0 1 0 --------------
0 1 1 --------------
1 0 0 0 0 0 0 1 0 1 1 0
1 0 1 0 0 1 0 1 0 0 1 0
1 1 0 0 0 1 1 1 1 0 0 0
?1 1 0 1 1 1 0 1 0 0 0 0?
1 1 1 --------------
Folgerung: Für gegebenes (R,R) und u0,s,r) können entweder
kein, oder ein oder mehrere Fixpunkte existieren.
3.2 Einen Fixpunkt der Abbildung ϕ2 nennt man ein solches
U ∈ M, für das gilt:
U ∈ {ϕ2U}.
Offenbar ist ein Fixpunkt der Abbildung ϕ auch ein Fixpunkt
der Abbildung ϕ2.
Betrachten wir den analytischen Ausdruck für ϕ2U.
Seien
ϕ(u01, s1,r1) U = Y, ϕ(u02,s2,r2) Y = V.
Dann erhalten wir aus dem System (1.1) für ɳ = 1,9:
y3ɳ-2 = u3ɳ-1 + r1 + s1∆ɳ +Tɳ(s1,up),
y3ɳ-1 = u3ɳ-2, y3ɳ = u3ɳ-1,
v3ɳ-2 = y3ɳ-3 + r2 + s2∆ɳ + Tɳ(s2,yp),
v3ɳ-1 = y3ɳ-2, v3ɳ = y3ɳ-1,
u0 = u01, y0 = u02.
Daraus folgt für ɳ = 1,9:
(1.6)
v3ɳ-2|ɳ>1 = u3ɳ-4 + r2 +s2∆ɳ +Tɳ(s2,yp)
v1 = u02 + r2 + s2∆1 + T1(s2,yp)
v3ɳ-1 = u3ɳ-3 + r1 + s1∆ɳ + Tɳ(s1,up)
v3ɳ u3ɳ-2.
Das Auffinden der Fixpunkte der Abbildung ϕ2, das ist die
Lösung des Systems (1.6) für V = U bezüglich der Unbekannten
u1, u2, … , u27.
Aus (1.6) ergeben sich notwendige Bedingungen für die Existenz
von Fixpunkten:
(N1) u3ɳ = u3ɳ-2, ɳ = 1,9,
(N2) u3R1-1 + u3R1-3 + r1 = 0 (wegen ∆R1 = TR1 = 0),
(N3) u3R1-2 + u3R1-4 + r2 = 0 wenn R1 ≠ 1 (wegen ∆R1 = TR1 = 0).
4. Zustandsklassen
4.1 Definition einer Zustandsklasse
Wir betrachten (P,R) als fest. Ir setzen (P,R) ∈ PR vor-
aus, obwohl nicht überall in diesem Punkt diese Einschrän-
kung notwendig ist. Die Menge
bezeichnet, für welches
ϕU = U
für irgendeinen Parameterwert (u0,s,r) gilt.
Für Fixpunkte U hat das System (1.1) das Aussehen
(3.1)
U3ɳ-2 = U3ɳ-3 + r + s∆ɳ Tɳ(s,Up)
U3ɳ-1 = U3ɳ-2
U3ɳ = U3ɳ-1, n = 1,9.
Daraus ergeben sich notwendige Bedingungen für Fixpunkte:
(N1) U3ɳ-2 = U3ɳ-1 = U3ɳ, ɳ = 1,9
(N2) U3R1-2 + U3R1-3 + r = 0 (wegen ∆R1 = TR1 = 0)
Um für konkrete (P,R) und (u0,s,r) Fixpunkte zu finden, muß
das System (3.1) bezüglich der Unbekannten u1,u2,…,u27
gelöst werden, was keine prinzipiellen Schwierigkeiten
bereitet.
Für (P0,R0) werden alle Fixpunkte errechnet:
u0 s r u3 u6 u9 u12 u15 u18 u21 u24 u27
0 0 0 0 0 1 0 0 0 1 1 0
0 0 1 0 1 1 1 0 0 0 1 1
0 1 0 --------------
0 1 1 --------------
1 0 0 0 0 0 0 1 0 1 1 0
1 0 1 0 0 1 0 1 0 0 1 0
1 1 0 0 0 1 1 1 1 0 0 0
?1 1 0 1 1 1 0 1 0 0 0 0?
1 1 1 --------------
Folgerung: Für gegebenes (R,R) und u0,s,r) können entweder
kein, oder ein oder mehrere Fixpunkte existieren.
3.2 Einen Fixpunkt der Abbildung ϕ2 nennt man ein solches
U ∈ M, für das gilt:
U ∈ {ϕ2U}.
Offenbar ist ein Fixpunkt der Abbildung ϕ auch ein Fixpunkt
der Abbildung ϕ2.
Betrachten wir den analytischen Ausdruck für ϕ2U.
Seien
ϕ(u01, s1,r1) U = Y, ϕ(u02,s2,r2) Y = V.
Dann erhalten wir aus dem System (1.1) für ɳ = 1,9:
y3ɳ-2 = u3ɳ-1 + r1 + s1∆ɳ +Tɳ(s1,up),
y3ɳ-1 = u3ɳ-2, y3ɳ = u3ɳ-1,
v3ɳ-2 = y3ɳ-3 + r2 + s2∆ɳ + Tɳ(s2,yp),
v3ɳ-1 = y3ɳ-2, v3ɳ = y3ɳ-1,
u0 = u01, y0 = u02.
Daraus folgt für ɳ = 1,9:
(1.6)
v3ɳ-2|ɳ>1 = u3ɳ-4 + r2 +s2∆ɳ +Tɳ(s2,yp)
v1 = u02 + r2 + s2∆1 + T1(s2,yp)
v3ɳ-1 = u3ɳ-3 + r1 + s1∆ɳ + Tɳ(s1,up)
v3ɳ u3ɳ-2.
Das Auffinden der Fixpunkte der Abbildung ϕ2, das ist die
Lösung des Systems (1.6) für V = U bezüglich der Unbekannten
u1, u2, … , u27.
Aus (1.6) ergeben sich notwendige Bedingungen für die Existenz
von Fixpunkten:
(N1) u3ɳ = u3ɳ-2, ɳ = 1,9,
(N2) u3R1-1 + u3R1-3 + r1 = 0 (wegen ∆R1 = TR1 = 0),
(N3) u3R1-2 + u3R1-4 + r2 = 0 wenn R1 ≠ 1 (wegen ∆R1 = TR1 = 0).
4. Zustandsklassen
4.1 Definition einer Zustandsklasse
Wir betrachten (P,R) als fest. Ir setzen (P,R) ∈ PR vor-
aus, obwohl nicht überall in diesem Punkt diese Einschrän-
kung notwendig ist. Die Menge  läßt sich dann völlig in
disjunkte Teilmenge zerlegen, wobei in einer Teilmenge die-
jenigen Elemente aus
läßt sich dann völlig in
disjunkte Teilmenge zerlegen, wobei in einer Teilmenge die-
jenigen Elemente aus  enthalten sind, die bei ein- oder
mehrfacher Anwendung der Abbildung ϕ und ϕ-1 ineinander
übergehen. Dabei können die Abbildung bei wiederholter An-
wendung verschiedene Parameterwerte annehmen.
Die Teilmenge bezeichnen wir als Zustandsklassen des Chiffra-
tors. Von der Rechtmäßigkeit der Definition kann man sich über-
zeugen, indem man zum Beispiel die 8 Abbildung ϕ, die ver-
schiedenen Parameterwerten entsprechend, als Permutationen der
Menge
enthalten sind, die bei ein- oder
mehrfacher Anwendung der Abbildung ϕ und ϕ-1 ineinander
übergehen. Dabei können die Abbildung bei wiederholter An-
wendung verschiedene Parameterwerte annehmen.
Die Teilmenge bezeichnen wir als Zustandsklassen des Chiffra-
tors. Von der Rechtmäßigkeit der Definition kann man sich über-
zeugen, indem man zum Beispiel die 8 Abbildung ϕ, die ver-
schiedenen Parameterwerten entsprechend, als Permutationen der
Menge  betrachtet.
Wenden wir uns der Frage nach der Struktur der Zustandsklasse
und der Anzahl der Elemente in der Klasse zu.
Aufgrund der Voraussetzung (P,R) ∈ PR erweitern wir die Be-
zeichnungen {ϕnU} auf natürliche Art auf alle ganzzahligen n.
4.2. Die Mengen {ϕnU}
4.2.1 Aus der Definition der Abbildung ϕ ergibt sich die folgende
Darstellung für
Y = ϕ(u0,s,r) U ∈ {ϕU}:
(4.1)
2Y = (u0+r+s∆1+T1(s,Up), u3+r+s∆2+T2(s,Up), …
…, u24+r+s∆9+T9(s,Up))
1Y = 2U, 0Y = 1U.
Folgerungen: 1Y und 0Y hängen nicht von Parametern ab.
(4.2) Alle Komponenten von 2Y hängen von r ab;
eine Komponente -y1- hängt von u0 ab;
vier Komponenten hängen von s ab:
y3ɳ-2 für ɳ = R2,R3,R4,R5, falls Z(s,uP1,…,up5)
von s abhängt,
y3ɳ-2 für ɳ = R6,R7,R8,R9, falls Z(s,uP1,…,up5)
unabhängig von s ist.
(4.3) |{ϕU}| = |{2U}| < 8, |{1Y}| = |{0Y}| = 1.
Das heißt, bei verschiedenen Werten des Parame-
ters geht der Vektor U in verschiedene ϕU über.
(4.4) Für die 8 Vektoren 2Y nimmt jede Komponente zur
Hälfte die Werte 0 bzw. 1 an.
Seien Y = ϕ(u0,s,r) U ∈ {ϕU}, Y'=ϕ(u0+1,s,r)U
Y" = ϕ(u0),s+1,r)U, Y"' =ϕ(u0,s,r+1)U.
Dann gelten folgende Gleichungen:
(4.5) 1U = 0Y' = 0Y" = 0Y"';
2U = 1Y = 1Y' = 1Y" = 1Y"';
y
betrachtet.
Wenden wir uns der Frage nach der Struktur der Zustandsklasse
und der Anzahl der Elemente in der Klasse zu.
Aufgrund der Voraussetzung (P,R) ∈ PR erweitern wir die Be-
zeichnungen {ϕnU} auf natürliche Art auf alle ganzzahligen n.
4.2. Die Mengen {ϕnU}
4.2.1 Aus der Definition der Abbildung ϕ ergibt sich die folgende
Darstellung für
Y = ϕ(u0,s,r) U ∈ {ϕU}:
(4.1)
2Y = (u0+r+s∆1+T1(s,Up), u3+r+s∆2+T2(s,Up), …
…, u24+r+s∆9+T9(s,Up))
1Y = 2U, 0Y = 1U.
Folgerungen: 1Y und 0Y hängen nicht von Parametern ab.
(4.2) Alle Komponenten von 2Y hängen von r ab;
eine Komponente -y1- hängt von u0 ab;
vier Komponenten hängen von s ab:
y3ɳ-2 für ɳ = R2,R3,R4,R5, falls Z(s,uP1,…,up5)
von s abhängt,
y3ɳ-2 für ɳ = R6,R7,R8,R9, falls Z(s,uP1,…,up5)
unabhängig von s ist.
(4.3) |{ϕU}| = |{2U}| < 8, |{1Y}| = |{0Y}| = 1.
Das heißt, bei verschiedenen Werten des Parame-
ters geht der Vektor U in verschiedene ϕU über.
(4.4) Für die 8 Vektoren 2Y nimmt jede Komponente zur
Hälfte die Werte 0 bzw. 1 an.
Seien Y = ϕ(u0,s,r) U ∈ {ϕU}, Y'=ϕ(u0+1,s,r)U
Y" = ϕ(u0),s+1,r)U, Y"' =ϕ(u0,s,r+1)U.
Dann gelten folgende Gleichungen:
(4.5) 1U = 0Y' = 0Y" = 0Y"';
2U = 1Y = 1Y' = 1Y" = 1Y"';
y = y1 + 1, ɳ = 2,9: y'3ɳ-2 = y3n-2;
y"3R1-2 = y3R1-2,
y3ɳ-2 + 1 + c ɳ = R2,R3,R4,R5
y"3ɳ-2 = {
y3ɳ-2 + c ɳ = R6,R7,R8,R9
c = 0, wenn Z(s,uP1,…,up5) von s abhängt,
c = 1, wenn Z(s,uP1,…,up5) nicht von s abhängt;
ɳ = 1,9: y"'3ɳ-2 = y3ɳ-2 + 1.
4.2.2 Betrachteten wir {ϕ2U}
Seien Y = ϕ(u01,s1,r1) U, V = ϕ(u02,s2,r2) Y.
Dann sind
(4.6)
2V = (u01 + r2 + s2∆1 + T1(s2,Yp),
y3 + r2 + s2∆2 + T2(s2,Yp),…
…, y24 + r2 + s2∆9 + T9(s2,Yp))
1V = 2Y = (u0+r1+s1∆1+T1(s1,Up), …)
0V = 1Y = 2U.
Folgerungen:
(4.7) Alle Komponenten 2V hängen von r2 ab;
9 bis 17 Komponenten hängen von r1 ab: 1V und
möglicherweise einige Komponenten von 2V außer
v3R1-2;
eine Komponente -v1- hängt von u02 ab;
1 bis 9 Komponenten hängen von u01 ab: v2 und
möglicherweise einige Komponenten von 2V außer
v3R1-2;
4 Komponenten hängen von s2 ab: v3ɳ-2 entweder
für n=R2,R5 oder für ɳ = R6,R9;
4 bis 12 Komponenten hängen von s1 ab: v3ɳ-1
entweder für n = R2,R5 oder für n = R6,R9 und
möglicherweise einige Komponenten von 2V außer
v3R1-2.
(4.8) |{ϕ2U}| = 64, 8 ≤ |{2V}| ≤ 64, |{1V}| = 8, |{0V}| = 1.
(4.9) Wenn man alle 64 Vektoren V ∈ {ϕ2U} betrachtet,
dann nimmt jede Komponente der 64 Vektoren 0V
und der 64 Vektor 0V die Werte 0 und 1 zur
Hälfte an.
4.2.3 Wenn wir bei der Betrachtung von {ϕ3U}
die Bezeichnung
W = ϕ(u03, s3, r3)V einführen, dann erhalten wir für
W eine analoge Darstellung.
Insbesondere:
(4.10) 1W = 2V, 1V = 2Y.
Daraus folgt
(4.11) |{ϕ3U}| = 512, 8 ≤ |{2W}| ≤ 512, , 8 ≤ |{1W}| ≤ 64, |{0W}| = 8.
(4.12) In den 512 Vektoren W ∈ {ϕ3U} nimmt jede
Komponente die Werte 0 und 1 zur Hälfte an.
Aus (4.11) folgt, daß jede Zustandsklasse
mindestens 512 Elemente enthält.
4.2.4 Wir überlegen uns nun einige Eigenschaften der Elemente der
Menge {ϕ-nU} für n = 1,2,3. Sei Y = ϕ-1(u0,s,r)U.
Dann gilt infolge (4.1)
(4.13)
2Y = 1U, 1Y = 0U
aber eine explizite Darstellung für die Elemente von 0Y ist
nur dann möglich, wenn (P,R) fixiert ist. Die Elemente von
0Y genügen dem grundlegenden Gleichungssystem, siehe Punkt 2.1.
Folgerungen:
(4.14) Nur die Komponenten des Vektors 0Y können
von u0,s und r abhängen.
(4.15) |{ϕ-1U}| = |{0Y}| = 8, |{1Y}| = |{2Y}| = 1.
Beweis:
Seien ϕ1 ≠ ϕ2, ϕ
= y1 + 1, ɳ = 2,9: y'3ɳ-2 = y3n-2;
y"3R1-2 = y3R1-2,
y3ɳ-2 + 1 + c ɳ = R2,R3,R4,R5
y"3ɳ-2 = {
y3ɳ-2 + c ɳ = R6,R7,R8,R9
c = 0, wenn Z(s,uP1,…,up5) von s abhängt,
c = 1, wenn Z(s,uP1,…,up5) nicht von s abhängt;
ɳ = 1,9: y"'3ɳ-2 = y3ɳ-2 + 1.
4.2.2 Betrachteten wir {ϕ2U}
Seien Y = ϕ(u01,s1,r1) U, V = ϕ(u02,s2,r2) Y.
Dann sind
(4.6)
2V = (u01 + r2 + s2∆1 + T1(s2,Yp),
y3 + r2 + s2∆2 + T2(s2,Yp),…
…, y24 + r2 + s2∆9 + T9(s2,Yp))
1V = 2Y = (u0+r1+s1∆1+T1(s1,Up), …)
0V = 1Y = 2U.
Folgerungen:
(4.7) Alle Komponenten 2V hängen von r2 ab;
9 bis 17 Komponenten hängen von r1 ab: 1V und
möglicherweise einige Komponenten von 2V außer
v3R1-2;
eine Komponente -v1- hängt von u02 ab;
1 bis 9 Komponenten hängen von u01 ab: v2 und
möglicherweise einige Komponenten von 2V außer
v3R1-2;
4 Komponenten hängen von s2 ab: v3ɳ-2 entweder
für n=R2,R5 oder für ɳ = R6,R9;
4 bis 12 Komponenten hängen von s1 ab: v3ɳ-1
entweder für n = R2,R5 oder für n = R6,R9 und
möglicherweise einige Komponenten von 2V außer
v3R1-2.
(4.8) |{ϕ2U}| = 64, 8 ≤ |{2V}| ≤ 64, |{1V}| = 8, |{0V}| = 1.
(4.9) Wenn man alle 64 Vektoren V ∈ {ϕ2U} betrachtet,
dann nimmt jede Komponente der 64 Vektoren 0V
und der 64 Vektor 0V die Werte 0 und 1 zur
Hälfte an.
4.2.3 Wenn wir bei der Betrachtung von {ϕ3U}
die Bezeichnung
W = ϕ(u03, s3, r3)V einführen, dann erhalten wir für
W eine analoge Darstellung.
Insbesondere:
(4.10) 1W = 2V, 1V = 2Y.
Daraus folgt
(4.11) |{ϕ3U}| = 512, 8 ≤ |{2W}| ≤ 512, , 8 ≤ |{1W}| ≤ 64, |{0W}| = 8.
(4.12) In den 512 Vektoren W ∈ {ϕ3U} nimmt jede
Komponente die Werte 0 und 1 zur Hälfte an.
Aus (4.11) folgt, daß jede Zustandsklasse
mindestens 512 Elemente enthält.
4.2.4 Wir überlegen uns nun einige Eigenschaften der Elemente der
Menge {ϕ-nU} für n = 1,2,3. Sei Y = ϕ-1(u0,s,r)U.
Dann gilt infolge (4.1)
(4.13)
2Y = 1U, 1Y = 0U
aber eine explizite Darstellung für die Elemente von 0Y ist
nur dann möglich, wenn (P,R) fixiert ist. Die Elemente von
0Y genügen dem grundlegenden Gleichungssystem, siehe Punkt 2.1.
Folgerungen:
(4.14) Nur die Komponenten des Vektors 0Y können
von u0,s und r abhängen.
(4.15) |{ϕ-1U}| = |{0Y}| = 8, |{1Y}| = |{2Y}| = 1.
Beweis:
Seien ϕ1 ≠ ϕ2, ϕ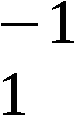 U = U1, ϕ
U = U1, ϕ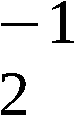 = U, U1 = U2
Dann gilt ϕ1U1 = ϕ2U2 = ϕ2U1, was jedoch (4.3) widerspricht.
Analog kann man beweisen:
(4.16)
|{ϕ-2U}| = 64
(4.17)
|{ϕ-3U}| = 512
4.2.5 Wir weisen jetzt einige Eigenschaften der Menge {ϕn),U}
im allgemeinen Fall nach. Zur Vereinfachung der Schreibweise
bezeichnen wir
|{ϕn)U}| = μn)U.
Zuerst fixieren wir die offensichtlichen Ungleichungen
(4.18)
μ±nU ≤ 23n,
(4.19)
μ±nU ≤ 227
die aus der Definition von {ϕn)U} und aus Gleichung
|
= U, U1 = U2
Dann gilt ϕ1U1 = ϕ2U2 = ϕ2U1, was jedoch (4.3) widerspricht.
Analog kann man beweisen:
(4.16)
|{ϕ-2U}| = 64
(4.17)
|{ϕ-3U}| = 512
4.2.5 Wir weisen jetzt einige Eigenschaften der Menge {ϕn),U}
im allgemeinen Fall nach. Zur Vereinfachung der Schreibweise
bezeichnen wir
|{ϕn)U}| = μn)U.
Zuerst fixieren wir die offensichtlichen Ungleichungen
(4.18)
μ±nU ≤ 23n,
(4.19)
μ±nU ≤ 227
die aus der Definition von {ϕn)U} und aus Gleichung
| | = 227 folgen.
Theorem:
Wenn für gegebenes natürliches n für alle U ∈
| = 227 folgen.
Theorem:
Wenn für gegebenes natürliches n für alle U ∈  μnU = 23n gilt, so gilt für alle U ∈
μnU = 23n gilt, so gilt für alle U ∈  (4.20)
μ-nU = μnU = 23n.
Beweis:
Sei μ-nU1 < 23n. Dann existieren U2 ∈
(4.20)
μ-nU = μnU = 23n.
Beweis:
Sei μ-nU1 < 23n. Dann existieren U2 ∈  :
ϕ
:
ϕ ϕ
ϕ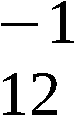 … ϕ
… ϕ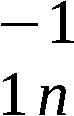 U1 = U2 = ϕ
U1 = U2 = ϕ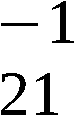 ϕ
ϕ … ϕ
… ϕ U1
und es gilt nicht gleichzeitig ϕ1i = ϕ2i für alle i = 1,n.
Aber dann gilt U1 = ϕ1n … ϕ12ϕ11 U2 = ϕ2n … ϕ22ϕ21U2
was μnU2 = 23n widerspricht.
Theorem:
Für natürliches n gilt
(4.21)
μnU ≤ μn+1 U,
(4.22)
μ-n ≤ μ-n-1 U.
Beweis:
Wir bezeichnen die Elemente {ϕnU} mit V1,V2, …,Vm.
Sei ϕ0 = ϕ(0,0,0). Dann gilt ϕ0Vi ≠ ϕ0Vh
für alle i ≠ j, i = 1,m, j = 1,m. Deshalb gilt
μnU = |{ϕ0V1, ϕ0V2, …, ϕ0Vm}|.
Andererseits gilt
{μ0V1,μ0V2,…,μ0Vm} ≤ {ϕn+1U},
woraus die erste Behauptung des Theorems folgt. Die
zweite wird analog bewiesen.
4.3 Mengen {ϕU1U2} und {ϕ-1ϕU}
Zur Vereinfachung der Schreibweise bezeichnen wir
{ϕU1U2} = {ϕU1} ^ {ϕU2 }; U1 ∈
U1
und es gilt nicht gleichzeitig ϕ1i = ϕ2i für alle i = 1,n.
Aber dann gilt U1 = ϕ1n … ϕ12ϕ11 U2 = ϕ2n … ϕ22ϕ21U2
was μnU2 = 23n widerspricht.
Theorem:
Für natürliches n gilt
(4.21)
μnU ≤ μn+1 U,
(4.22)
μ-n ≤ μ-n-1 U.
Beweis:
Wir bezeichnen die Elemente {ϕnU} mit V1,V2, …,Vm.
Sei ϕ0 = ϕ(0,0,0). Dann gilt ϕ0Vi ≠ ϕ0Vh
für alle i ≠ j, i = 1,m, j = 1,m. Deshalb gilt
μnU = |{ϕ0V1, ϕ0V2, …, ϕ0Vm}|.
Andererseits gilt
{μ0V1,μ0V2,…,μ0Vm} ≤ {ϕn+1U},
woraus die erste Behauptung des Theorems folgt. Die
zweite wird analog bewiesen.
4.3 Mengen {ϕU1U2} und {ϕ-1ϕU}
Zur Vereinfachung der Schreibweise bezeichnen wir
{ϕU1U2} = {ϕU1} ^ {ϕU2 }; U1 ∈  , U2 ∈
, U2 ∈  .
Die Menge {ϕ-1ϕU} definieren wir - entsprechend anderen
Mengenbezeichnung - als Vereinigung der Mengen {ϕ-1Yi}, i = 1,8
wenn mit Yi die Elemente der Mengen {ϕU} bezeichnet werden.
Wir überlegen uns die Eigenschaften dieser Mengen.
(4.31)
0 ≤ |{ϕU1U2}| ≤ 8
Dies gilt offensichtlich aufgrund |{ϕU1U2}| ≤ |{ϕU1}| = 8.
Folgende Aussagen sind gleichbedeutend:
(4,32)
|{ϕU1U2}| > 0, U1 ∈ {ϕ-1ϕU2}, U2 ∈{ϕ-1ϕU1}.
Beweis:
ϕ1U1 = ϕ2U2 ↔ U1 = ϕ
.
Die Menge {ϕ-1ϕU} definieren wir - entsprechend anderen
Mengenbezeichnung - als Vereinigung der Mengen {ϕ-1Yi}, i = 1,8
wenn mit Yi die Elemente der Mengen {ϕU} bezeichnet werden.
Wir überlegen uns die Eigenschaften dieser Mengen.
(4.31)
0 ≤ |{ϕU1U2}| ≤ 8
Dies gilt offensichtlich aufgrund |{ϕU1U2}| ≤ |{ϕU1}| = 8.
Folgende Aussagen sind gleichbedeutend:
(4,32)
|{ϕU1U2}| > 0, U1 ∈ {ϕ-1ϕU2}, U2 ∈{ϕ-1ϕU1}.
Beweis:
ϕ1U1 = ϕ2U2 ↔ U1 = ϕ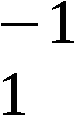 ϕ2U2 ↔ U2 = ϕ
ϕ2U2 ↔ U2 = ϕ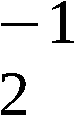 ϕ1U1.
|{ϕU1U2}| > 0 ist gleichbedeutend damit, daß
V ∈ {ϕU1U2} existiert mit U1 ∈ {ϕ-1V}, U2 ∈ {ϕ-1V}
Das ist offensichtlich. Sei dazu V = (vα)
ϕ1U1.
|{ϕU1U2}| > 0 ist gleichbedeutend damit, daß
V ∈ {ϕU1U2} existiert mit U1 ∈ {ϕ-1V}, U2 ∈ {ϕ-1V}
Das ist offensichtlich. Sei dazu V = (vα) ,
V = ϕ(u01,s1,r1)U1 = ϕ(u02,s2,r2)U2.
Wir suchen andere Elemente, die in der Menge {ϕU1U2}
liegen. Wir betrachten V1 = ϕ(u02,s2,r2 + 1)U1 und
V2 = ϕ(u01 + 1,s1,r1)U1.
Es gilt
(4.33)
V1 ∈{ϕU1U2} und V1 = ϕ(u02, s2,r2+1)U2
Es gilt
(4.34)
V2 ∈{ϕU1U2} und V2 = ϕ(u02+1,s2,r2)U2
Das folgt aus (4.5).
Ein analoges Resultat für den Parameter s zu erhalten, ist
aufgrund der Eigenschaften der Funktion Z komplizierter.
Man muß zwei Fälle unterscheiden:
(A) Die beiden Funktionen Z(s,u1P1,…,u1P5) und
Z(s,u2P1,…,u2p5) hängen beide von s ab
oder sind beide unabhängig von s;
(B) Eine der Funktionen hängt von s ab, die andere nicht.
Wir bemerken, daß apriori unbekannt ist, ob man für
gegebenes P beide Fälle unter der Bedingung |{ϕU1U2}| > 0
realisieren kann.
Wir betrachten V3 = ϕ(u01,s1+1,r1)U1.
Theorem: V3 ∈ {ϕU1U2} gilt genau dann, wenn
(A) erfüllte ist. In diesem Fall gilt
(4.35)
V3 = ϕ(u02,s2+1,r2)U2.
Beweis:
Nach Definition von V haben wir für ɳ=1,9,
u
,
V = ϕ(u01,s1,r1)U1 = ϕ(u02,s2,r2)U2.
Wir suchen andere Elemente, die in der Menge {ϕU1U2}
liegen. Wir betrachten V1 = ϕ(u02,s2,r2 + 1)U1 und
V2 = ϕ(u01 + 1,s1,r1)U1.
Es gilt
(4.33)
V1 ∈{ϕU1U2} und V1 = ϕ(u02, s2,r2+1)U2
Es gilt
(4.34)
V2 ∈{ϕU1U2} und V2 = ϕ(u02+1,s2,r2)U2
Das folgt aus (4.5).
Ein analoges Resultat für den Parameter s zu erhalten, ist
aufgrund der Eigenschaften der Funktion Z komplizierter.
Man muß zwei Fälle unterscheiden:
(A) Die beiden Funktionen Z(s,u1P1,…,u1P5) und
Z(s,u2P1,…,u2p5) hängen beide von s ab
oder sind beide unabhängig von s;
(B) Eine der Funktionen hängt von s ab, die andere nicht.
Wir bemerken, daß apriori unbekannt ist, ob man für
gegebenes P beide Fälle unter der Bedingung |{ϕU1U2}| > 0
realisieren kann.
Wir betrachten V3 = ϕ(u01,s1+1,r1)U1.
Theorem: V3 ∈ {ϕU1U2} gilt genau dann, wenn
(A) erfüllte ist. In diesem Fall gilt
(4.35)
V3 = ϕ(u02,s2+1,r2)U2.
Beweis:
Nach Definition von V haben wir für ɳ=1,9,
u = u01, u
= u01, u = u02:
v3ɳ-2 = u
= u02:
v3ɳ-2 = u +r1+s1∆ɳ+Tɳ(s1,U1P) = u
+r1+s1∆ɳ+Tɳ(s1,U1P) = u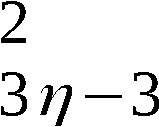 +r2+s2∆ɳ+Tɳ(s2,U2P).
Sei (A)erfüllt. Dann folgt hieraus und aus der Defini-
tion von V3 für ɳ=1,9
(4.36)
v
+r2+s2∆ɳ+Tɳ(s2,U2P).
Sei (A)erfüllt. Dann folgt hieraus und aus der Defini-
tion von V3 für ɳ=1,9
(4.36)
v = u
= u +r1+(s1+1)∆ɳ+Tɳ(s1+1,U1P) = u
+r1+(s1+1)∆ɳ+Tɳ(s1+1,U1P) = u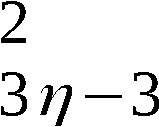 +r2+(s2+1)∆ɳ+Tɳ(s2+1,U2P).
Dies ist schon die zu beweisende Beziehung.
Sei (B) erfüllt, dann gilt im Unterschied zu (A) für
n ≠ R1
Tɳ(s1U1P) + Tɳ(s2,U2p) + Tɳ(s1+1,U1P) + Tɳ(s2+1,U1P) = 1
Anstelle von (4.36) erhalten wir für n ≠ R1
v
+r2+(s2+1)∆ɳ+Tɳ(s2+1,U2P).
Dies ist schon die zu beweisende Beziehung.
Sei (B) erfüllt, dann gilt im Unterschied zu (A) für
n ≠ R1
Tɳ(s1U1P) + Tɳ(s2,U2p) + Tɳ(s1+1,U1P) + Tɳ(s2+1,U1P) = 1
Anstelle von (4.36) erhalten wir für n ≠ R1
v = u
= u +r1+(s1+1)∆ɳ+Tɳ(s1+1,U1P) = 1 + u
+r1+(s1+1)∆ɳ+Tɳ(s1+1,U1P) = 1 + u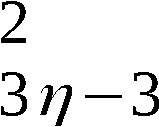 +r2+(s2+1)∆ɳ+Tɳ(s2+1,U2P).
Hieraus folgt V3 ≠ ϕ(u02 + a, s2,r2 + b)U2
für alle (a,b) ∈ {0,1}2, wie unschwer zu erkennen ist,
wenn man das Gegenteil annimmt.
Außerdem gilt V3 ≠ ϕ(u02 + a, s2, r2 + b)U2 für alle
(a,b) ∈ {0,1}2, da V3 ≠ V, V3 ≠ V1, V3 ≠ V2
per Definition gilt, woraus weiter folgt
V3 ≠ ϕ(u02+1, s2, r2 + 1)U2.
Deshalb liegt V3 nicht in der Menge {ϕ U2}.
Aufgrund der vorausgesetzten Resultate kann man
|{ϕU1U2}| ausrechnen.
Theorem:
Wir nehmen U1 ∈
+r2+(s2+1)∆ɳ+Tɳ(s2+1,U2P).
Hieraus folgt V3 ≠ ϕ(u02 + a, s2,r2 + b)U2
für alle (a,b) ∈ {0,1}2, wie unschwer zu erkennen ist,
wenn man das Gegenteil annimmt.
Außerdem gilt V3 ≠ ϕ(u02 + a, s2, r2 + b)U2 für alle
(a,b) ∈ {0,1}2, da V3 ≠ V, V3 ≠ V1, V3 ≠ V2
per Definition gilt, woraus weiter folgt
V3 ≠ ϕ(u02+1, s2, r2 + 1)U2.
Deshalb liegt V3 nicht in der Menge {ϕ U2}.
Aufgrund der vorausgesetzten Resultate kann man
|{ϕU1U2}| ausrechnen.
Theorem:
Wir nehmen U1 ∈  und U2 ∈
und U2 ∈  so an, daß |{ϕU1U2}| > 0
gilt. Dann gilt im Fall (A)
(4.37)
|{ϕU1U2}| = 8, d.h. {sU2} = {ϕU2}.
(4.38)
Im Fall (B) gilt |{ϕU1U2}| = 4
Beweis:
Sei Vabc = ϕ(u0 + a, s+b, r+c)U1, (abc) ∈ {0,1}3.
Wenn V000 Element {ϕ,U1U2}, dann liegen aufgrund von (4.33)
und (4.34) in dieser Menge auch V100,U001 und V101.
Aus dem vorigen Theorem folgt, daß V010,V110,U011
und V111 im Fall (A) in der Menge {ϕU1U2} liegen und
im Fall (B) nicht in dieser Menge liegen.
Bis jetzt habe wir feste U1 und U2 betrachtet. Jetzt
betrachten wir für gegebenes U1 alle U2, für die
|{ϕU1U2} > 0 gilt.
Das heißt, wir betrachten {ϕ-1sU}.
Theorem:
(4.39)
8 ≤ |{ϕ-1sU}| ≤ 16
Beweis:
(I) Wir bezeichnen V = ϕ(u01,s1,r1)U,
W = ϕ-1(u02,s2,r2)V.
Dann gilt nach Definition ϕ
2U = 1V = 1U = 0V = 1W,
v3ɳ-2=u3ɳ-3+r1+s1∆ɳTɳ(s1,Up)=
= w3ɳ-3+r2+s2∆ɳ+Tɳ(s2,Wp), (ɳ = 1,9)
u0 = u01, w0 = u02.
Variabel sind nur die Elemente von 0W.
Sie genügen den Gleichungen
u3ɳ-3+w3ɳ-3+r1+r2+(s1+s2)∆ɳ+Tɳ(s1,Up)+Tɳ(s2,Wp)= 0.
Wenn die Parameter (u01,s1,r1,u02,s2,r2) die Menge
{0,1}6 durchlaufen, dann ist offensichtlich 0W
ein und dasselbe für (r1,r2) = (r1+1,r2+1) und auch für
(u01,u02) = (u01+1,u02+1).
Das heißt, faktisch gibt es nur vier freie Parameter,
deshalb gilt |{ϕ-1ϕU}| ≤ 24 = 16.
(2) Sei V ∈{ϕ,U} fest. Dann gilt {ϕ-1V} ≤ {ϕ-1ϕU}.
Deshalb ist 8 = |{ϕ-1V}| ≤ |{ϕ-1ϕU}.
5. Der Spezialfall (P0,R0)
5.1. Viele Probleme lassen sich wesentlich einfacher lösen, wenn
wir (P,R) nicht als beliebig, sondern als fest annehmen.
Außerdem weist in einigen Fällen der Lösungsweg eines Problems
für festes (P,R) auf den Lösungsweg dieses Problems für be-
liebiges (P,R) oder zumindest für eine gewisse Klasse von
(P,R) hin.
Indem wir berücksichtigen, daß (P,R) Langzeitschlüssel sind,
ist die Untersuchung der kryptologischen Schaltung für
(P0,R0), für die vorgesehenen ist, sie als Langzeitschlüssel
im Muster des Chiffrators zu benutzen, völlig gerechtfertigt.
5.2. Für (P,R) = (P0,R0) nimmt das System (1.1) zur Definition
der Abbildung ϕ(u0,s,r)U=Y folgende Gestalt an:
(5.1)
(a) y1=u0+s+r+u15+u21+u24+u27+Z0+Z1+Z2+Z3
(b) y4=r+u3+u27+Z0+Z1
(c) y7=s+r+u6+u15+u24+u27+Z0+Z1+Z2+Z3
(d) y10=s+r+u9+u24+u27+Z0+Z1+Z2
(e) y13=r+u12+Z0
(f) y16=r+u15+u27+Z0
(g) y19=s+r+u15+u18+u24+u27+Z0+Z1+Z2
(h) y22=r+u21
(i) y25=r+u27+Z0+Z1
(j) y3ɳ-1=u3ɳ-2, y3ɳ=u3ɳ-1 (ɳ=1,9).
Zur Vereinfachung der Schreibweise werden hier folgende
Bezeichnungen benutzt.
Z0 = Z(s,u22,u7,u18,u2,u16)
Z1 = Z(u23,u3,u14,u1,u13,u25)
Z2 = Z(u12,u17,u4,u11,u9,u26)
Z3 = Z(u10,u19,u8,u5,u20,u6)
Aufgrund der hinreichenden Bedingung (D8) im Punkt 2.3
gilt (P0,R0) ∈ PR, d.h., die Abbildung ϕ ist eineindeutig.
Das grundlegende Gleichungssystem nimmt folgenden Gestalt an:
(5.2)
(a) 0 = u21+y22+r
(b) 0 = u12+u21+Z0+y13+y22
(c) 0 = u15+u12+u27+y16+y13
(d) 0 = u3+u15+Z1+y4+y16
(e) 0 = u3+y25+y4
(f) 0 = u9+u24+Z2+s+y10+y25
(g) 0 = u18+u9+u15+y19+y10
(h) 0 = u6+u18+Z3+y7+y19
(i) 0 = u0+u6+u21+y1+y7
Hieraus erhalten wird das Gleichungssystem für die
Abbildung ϕ-1(u0,s,r)Y = U.
Zur Vereinfachung der Schreibweise setzen wir
Z4 = Z(y24,y4,y25,y15,y2,y14,y26)
Z5 = Z(y11,y20,y9,y6,y21,u0+r+y1+y7+y22)
Z6 = Z(s,y23,y8,u0+r+y1+y19+y22+Z5,y3,y17)
Z7 = Z(r+y13+Z6,y18,y5,y12,u0+r+y1+y10+y16+y22+y25+Z4+Z5,y27).
Dann gilt
(5.3)
(a) u3 = y4+y25
(b) u6 = u0+r+y1+y7+y22
(c) u9 = u0+r+y1+y10+y16+y22+y25+Z4+Z5
(d) u12 = r+y13+Z6
(e) u15 = y16+y25+Z4
(f) u18 = u0+r+y1+y19+y22+Z5
(g) u21 = r+y22
(h) u24 = u0+r+y1+y16+y22+Z4+Z5+Z7
(i) u27 = r+y25+Z4+Z6
(j) u3ɳ-1 = y3ɳ-1, u3ɳ-1 = y3ɳ (ɳ = 1,9)
5.3 Ausgehend vom Gegenteil, zeigen wir
|{ϕ4U}| = 212.
Sei V ∈ {ϕ4U} und V kann aus U nach 4 Schritten
auf zwei verschiedenen Wegen erhalten:
so an, daß |{ϕU1U2}| > 0
gilt. Dann gilt im Fall (A)
(4.37)
|{ϕU1U2}| = 8, d.h. {sU2} = {ϕU2}.
(4.38)
Im Fall (B) gilt |{ϕU1U2}| = 4
Beweis:
Sei Vabc = ϕ(u0 + a, s+b, r+c)U1, (abc) ∈ {0,1}3.
Wenn V000 Element {ϕ,U1U2}, dann liegen aufgrund von (4.33)
und (4.34) in dieser Menge auch V100,U001 und V101.
Aus dem vorigen Theorem folgt, daß V010,V110,U011
und V111 im Fall (A) in der Menge {ϕU1U2} liegen und
im Fall (B) nicht in dieser Menge liegen.
Bis jetzt habe wir feste U1 und U2 betrachtet. Jetzt
betrachten wir für gegebenes U1 alle U2, für die
|{ϕU1U2} > 0 gilt.
Das heißt, wir betrachten {ϕ-1sU}.
Theorem:
(4.39)
8 ≤ |{ϕ-1sU}| ≤ 16
Beweis:
(I) Wir bezeichnen V = ϕ(u01,s1,r1)U,
W = ϕ-1(u02,s2,r2)V.
Dann gilt nach Definition ϕ
2U = 1V = 1U = 0V = 1W,
v3ɳ-2=u3ɳ-3+r1+s1∆ɳTɳ(s1,Up)=
= w3ɳ-3+r2+s2∆ɳ+Tɳ(s2,Wp), (ɳ = 1,9)
u0 = u01, w0 = u02.
Variabel sind nur die Elemente von 0W.
Sie genügen den Gleichungen
u3ɳ-3+w3ɳ-3+r1+r2+(s1+s2)∆ɳ+Tɳ(s1,Up)+Tɳ(s2,Wp)= 0.
Wenn die Parameter (u01,s1,r1,u02,s2,r2) die Menge
{0,1}6 durchlaufen, dann ist offensichtlich 0W
ein und dasselbe für (r1,r2) = (r1+1,r2+1) und auch für
(u01,u02) = (u01+1,u02+1).
Das heißt, faktisch gibt es nur vier freie Parameter,
deshalb gilt |{ϕ-1ϕU}| ≤ 24 = 16.
(2) Sei V ∈{ϕ,U} fest. Dann gilt {ϕ-1V} ≤ {ϕ-1ϕU}.
Deshalb ist 8 = |{ϕ-1V}| ≤ |{ϕ-1ϕU}.
5. Der Spezialfall (P0,R0)
5.1. Viele Probleme lassen sich wesentlich einfacher lösen, wenn
wir (P,R) nicht als beliebig, sondern als fest annehmen.
Außerdem weist in einigen Fällen der Lösungsweg eines Problems
für festes (P,R) auf den Lösungsweg dieses Problems für be-
liebiges (P,R) oder zumindest für eine gewisse Klasse von
(P,R) hin.
Indem wir berücksichtigen, daß (P,R) Langzeitschlüssel sind,
ist die Untersuchung der kryptologischen Schaltung für
(P0,R0), für die vorgesehenen ist, sie als Langzeitschlüssel
im Muster des Chiffrators zu benutzen, völlig gerechtfertigt.
5.2. Für (P,R) = (P0,R0) nimmt das System (1.1) zur Definition
der Abbildung ϕ(u0,s,r)U=Y folgende Gestalt an:
(5.1)
(a) y1=u0+s+r+u15+u21+u24+u27+Z0+Z1+Z2+Z3
(b) y4=r+u3+u27+Z0+Z1
(c) y7=s+r+u6+u15+u24+u27+Z0+Z1+Z2+Z3
(d) y10=s+r+u9+u24+u27+Z0+Z1+Z2
(e) y13=r+u12+Z0
(f) y16=r+u15+u27+Z0
(g) y19=s+r+u15+u18+u24+u27+Z0+Z1+Z2
(h) y22=r+u21
(i) y25=r+u27+Z0+Z1
(j) y3ɳ-1=u3ɳ-2, y3ɳ=u3ɳ-1 (ɳ=1,9).
Zur Vereinfachung der Schreibweise werden hier folgende
Bezeichnungen benutzt.
Z0 = Z(s,u22,u7,u18,u2,u16)
Z1 = Z(u23,u3,u14,u1,u13,u25)
Z2 = Z(u12,u17,u4,u11,u9,u26)
Z3 = Z(u10,u19,u8,u5,u20,u6)
Aufgrund der hinreichenden Bedingung (D8) im Punkt 2.3
gilt (P0,R0) ∈ PR, d.h., die Abbildung ϕ ist eineindeutig.
Das grundlegende Gleichungssystem nimmt folgenden Gestalt an:
(5.2)
(a) 0 = u21+y22+r
(b) 0 = u12+u21+Z0+y13+y22
(c) 0 = u15+u12+u27+y16+y13
(d) 0 = u3+u15+Z1+y4+y16
(e) 0 = u3+y25+y4
(f) 0 = u9+u24+Z2+s+y10+y25
(g) 0 = u18+u9+u15+y19+y10
(h) 0 = u6+u18+Z3+y7+y19
(i) 0 = u0+u6+u21+y1+y7
Hieraus erhalten wird das Gleichungssystem für die
Abbildung ϕ-1(u0,s,r)Y = U.
Zur Vereinfachung der Schreibweise setzen wir
Z4 = Z(y24,y4,y25,y15,y2,y14,y26)
Z5 = Z(y11,y20,y9,y6,y21,u0+r+y1+y7+y22)
Z6 = Z(s,y23,y8,u0+r+y1+y19+y22+Z5,y3,y17)
Z7 = Z(r+y13+Z6,y18,y5,y12,u0+r+y1+y10+y16+y22+y25+Z4+Z5,y27).
Dann gilt
(5.3)
(a) u3 = y4+y25
(b) u6 = u0+r+y1+y7+y22
(c) u9 = u0+r+y1+y10+y16+y22+y25+Z4+Z5
(d) u12 = r+y13+Z6
(e) u15 = y16+y25+Z4
(f) u18 = u0+r+y1+y19+y22+Z5
(g) u21 = r+y22
(h) u24 = u0+r+y1+y16+y22+Z4+Z5+Z7
(i) u27 = r+y25+Z4+Z6
(j) u3ɳ-1 = y3ɳ-1, u3ɳ-1 = y3ɳ (ɳ = 1,9)
5.3 Ausgehend vom Gegenteil, zeigen wir
|{ϕ4U}| = 212.
Sei V ∈ {ϕ4U} und V kann aus U nach 4 Schritten
auf zwei verschiedenen Wegen erhalten:
| | (u01,s1,r1) | u(02,s2,r2) | u(03,s3,r3) | | |
| / | X1 | X2 | X3 | \ | |
| U | / | | | V | \ | (u04,s4,r4)
(u'04,s'4,r'4) |
| \ | | | / |
| \ | Y1 | Y2 | Y3 | / | |
| | (u'01,s ,r ,r ) ) | u'(02,s ,r'2) ,r'2) | u'(03,s'3,r'3) | | |
X1 = ϕ(u01,s1,r1)U; Y1=ϕ(u ,s
,s ,r
,r )U
X2 = ϕ(u02,s2,r2)X1; Y2=ϕ(u
)U
X2 = ϕ(u02,s2,r2)X1; Y2=ϕ(u ,s
,s ,r
,r )Y1
X3 = ϕ(u03,s3,r3)X2; Y3=ϕ(u
)Y1
X3 = ϕ(u03,s3,r3)X2; Y3=ϕ(u ,s
,s ,r
,r )Y2
V = ϕ(u04,s4,r4)X3 = ϕ(u
)Y2
V = ϕ(u04,s4,r4)X3 = ϕ(u ,s
,s ,r
,r )Y3
Xi ≠ Yi für zumindest ein i ∈ {1,2,3}.
Aus dieser Voraussetzung folgt aufgrund (4.8) und (4.11)
Xi ≠ Yi für alle i = 1,3;
(5.5)
aufgrund von (4.1), (4.6) und (4.19) gilt
(5.6)
2U = 1X1 = 0X2 = 1Y1 = 0Y2
1U = 0X1 = 0Y1
2X1 = 1X2 = 0X3
2Y1 = 1Y2 = 0Y3
2X2 = 1X3 = 0V = 2Y2 = 1Y3
2X3 = 1V = 2Y3
(5.7)
aufgrund (5.5) 2X1 ≠ 2Y1, 1X2 ≠ 1Y2, 0X3 ≠ 0Y3
Im weiteren benutzen wir von diesen Beziehungen nur
(5.8)
0X3 = 2Y1 ≠ 2Y1 = 0Y3
sei (s1+s
)Y3
Xi ≠ Yi für zumindest ein i ∈ {1,2,3}.
Aus dieser Voraussetzung folgt aufgrund (4.8) und (4.11)
Xi ≠ Yi für alle i = 1,3;
(5.5)
aufgrund von (4.1), (4.6) und (4.19) gilt
(5.6)
2U = 1X1 = 0X2 = 1Y1 = 0Y2
1U = 0X1 = 0Y1
2X1 = 1X2 = 0X3
2Y1 = 1Y2 = 0Y3
2X2 = 1X3 = 0V = 2Y2 = 1Y3
2X3 = 1V = 2Y3
(5.7)
aufgrund (5.5) 2X1 ≠ 2Y1, 1X2 ≠ 1Y2, 0X3 ≠ 0Y3
Im weiteren benutzen wir von diesen Beziehungen nur
(5.8)
0X3 = 2Y1 ≠ 2Y1 = 0Y3
sei (s1+s ∆ɳ + Tɳ(s1,Up) + Tɳ(s
∆ɳ + Tɳ(s1,Up) + Tɳ(s ,Up) = Hɳ.
Nach Definition gilt für ɳ = 2,9
(5.9)
x
,Up) = Hɳ.
Nach Definition gilt für ɳ = 2,9
(5.9)
x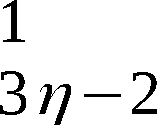 +y
+y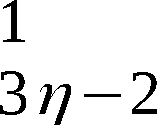 = r1 + r
= r1 + r + Hɳ = X
+ Hɳ = X + X
+ X und für ɳ = 1 gilt
(5.10)
x
und für ɳ = 1 gilt
(5.10)
x + y
+ y = u01+u
= u01+u +r1+r
+r1+r +H1 = x
+H1 = x + y
+ y Für s1 = s
Für s1 = s ist offensichtlich Hɳ = 0, ɳ = 1,9.
Für s1 ≠ s
ist offensichtlich Hɳ = 0, ɳ = 1,9.
Für s1 ≠ s erhalten wir für ɳ = 1,9, ɳ ≠ R1:
Hɳ = ∆ɳ + Z(0,uP1,…,up5) + Z(1,uP1,…,up5),
und HR1 = 0. Das heißt,
c für ɳ = R2,R3,R4,R5
Hɳ {
c+1 für ɳ = R6,R7,R8,R9,
wobei c ∈ {0,1} nur von U und P abhängt. Für R = R0
gilt
c für ɳ = 2,5,6,9
Hɳ {
c+1 für ɳ = 1,3,4,7
und H8 = 0.
Aufgrund (5.8) und (5.9) gilt dann
x
erhalten wir für ɳ = 1,9, ɳ ≠ R1:
Hɳ = ∆ɳ + Z(0,uP1,…,up5) + Z(1,uP1,…,up5),
und HR1 = 0. Das heißt,
c für ɳ = R2,R3,R4,R5
Hɳ {
c+1 für ɳ = R6,R7,R8,R9,
wobei c ∈ {0,1} nur von U und P abhängt. Für R = R0
gilt
c für ɳ = 2,5,6,9
Hɳ {
c+1 für ɳ = 1,3,4,7
und H8 = 0.
Aufgrund (5.8) und (5.9) gilt dann
x + y
+ y = x
= x + y
+ y = x
= x + y
+ y = x
= x + y
+ y .
x
.
x + y
+ y = x
= x + y
+ y = x
= x + y
+ y Aus (5.3e) folgt
x
Aus (5.3e) folgt
x = y
= y , deshalb x
, deshalb x = y
= y , x
, x = y
= y , x
, x + y
+ y .
Hieraus und aus (5.2.g) folgt x
.
Hieraus und aus (5.2.g) folgt x = y
= y , deshalb
x
, deshalb
x = y
= y , x
, x = y
= y Und jetzt erhalten wir aus (5.9) für s1 ≠ s
Und jetzt erhalten wir aus (5.9) für s1 ≠ s den Widerspruch:
für ɳ = 2 ist 0 = r1+r
den Widerspruch:
für ɳ = 2 ist 0 = r1+r + c,
für ɳ = 3 ist 0 = r1+r
+ c,
für ɳ = 3 ist 0 = r1+r + c+1.
für s1 = s
+ c+1.
für s1 = s folgt aus (5.9) r1 = r
folgt aus (5.9) r1 = r . Aber wegen (5.3.a)
gilt x
. Aber wegen (5.3.a)
gilt x = y
= y , deshalb folgt aus (5.10) u01 = u
, deshalb folgt aus (5.10) u01 = u .
Dies widerspricht X1 ≠ Y1.
5.4. Fixpunkte bezüglich ϕ2
Mit Hilfe einer EDVA wurden Fixpunkt bezüglich ϕ2 berech-
net. Zu diesem Zweck wurde das System (1.6) in ein zur Pro
grammierung günstigeres System umgeformt, unter besonderer
Berücksichtigung der notwendigen Bedingung (N1).
Die Methode zur Lösung der Aufgabe bestand im Durchprobieren
von 212 Möglichkeiten für 12 freie Variablen. Es wurden 74
Fixpunkte erhalten. Darunter, wie es auch sein muß, alle
Fixpunkte der Abbildung ϕ, siehe Punkt 3.1.
Die Aufstellung der Fixpunkte kann man auf den folgenden
Seiten finden.
Dort bedeutet
PAR - das Parametertupel (u01, u02, s1, s2, r1, r2),
FREV - gewisse Freie Parameter, die man nicht berücksichtigen braucht,
U03 U06 … U27 - die Darstellung des Fixpunktes U = (u1, u2,…,u27),
ANZAHL FREV - die Anzahl der Fixpunkte für eine gegebenes PAR.
Das erhaltene Resultat zeigt, daß die Verteilung der Fixpunkte
ziemlich unregelmäßig ist, obwohl man auch einige Beziehungen
bemerken kann.
Erläuterung zum Wert PAR:
PAR 0 0 0 0 0 0
s11 s12 s21 s22 f1 f2
03.10.1973 PROJEKT:MODELLVERGLEICH PROGRAMM: S4057
PAR FREV U03 U06 U09 U12 U15 U18 U21 U24 U27
000000 000110 000 000 111 000 000 000 111 111 000
ANZAHL FREV: 1
000011 001011 000 111 111 111 000 000 000 111 111
110010 111 010 010 000 000 010 000 111 101
111011 111 101 101 000 000 101 000 111 010
ANZAHL FREV: 3
000101 111010 111 111 000 111 000 111 000 101 000
ANZAHL FREV: 1
000110 100110 101 010 111 101 000 010 111 101 000
101100 101 111 000 000 000 010 101 000 101
ANZAHL FREV: 2
000111 010010 010 000 010 000 000 010 000 111 101
ANZAHL FREV: 1
001001 011001 010 111 000 000 000 101 010 000 010
011100 010 101 111 010 000 101 111 010 000
ANZAHL FREV: 2
001010 111000 111 111 000 111 000 111 000 010 000
ANZAHL FREV: 1
001011 100011 101 000 101 000 000 101 000 111 010
ANZAHL FREV: 1
001111 001001 000 111 010 101 000 101 010 010 111
001111 000 111 101 010 000 010 101 101 111
ANZAHL FREV: 2
010000 100100 101 010 111 101 010 101 101 010 000
101010 101 111 010 000 010 101 010 101 101
ANZAHL FREV: 2
010001 010110 010 000 101 000 010 101 101 111 101
ANZAHL FREV: 1
010010 111010 111 111 000 111 010 000 010 111 000
ANZAHL FREV: 1
010011 010000 010 000 010 010 010 000 010 010 101
011110 010 101 111 010 010 010 101 101 000
111001 111 101 101 000 010 010 010 010 010
ANZAHL FREV: 3
011000 010111 010 010 000 111 010 111 101 101 111
ANZAHL FREV: 1
011000 010101 010 010 000 111 010 111 101 010 111
011101 010 111 010 000 010 010 101 010 010
101001 101 101 010 101 010 010 000 000 111
ANZAHL FREV: 3
011100 001001 000 111 010 101 010 010 000 000 111
110000 111 010 111 010 010 000 000 000 101
ANZAHL FREV: 2
011101 000001 000 010 101 111 010 101 010 000 010
110111 111 000 000 010 010 101 101 111 111
ANZAHL FREV: 2
011110 001011 000 111 111 111 010 111 010 111 111
ANZAHL FREV: 1
100000 011010 010 101 111 010 101 010 010 101 000
011101 010 111 101 000 101 010 101 010 010
ANZAHL FREV: 2
100001 111110 111 111 000 111 101 000 101 111 000
ANZAHL FREV: 1
100010 100011 101 000 010 000 101 010 010 111 010
ANZAHL FREV: 1
100011 100000 101 010 111 101 101 101 010 010 000
100111 101 000 101 101 101 000 101 101 010
110110 111 010 010 000 101 101 101 101 101
ANZAHL FREV: 3
100100 010001 010 010 101 010 101 101 000 000 111
101010 101 111 101 000 101 101 010 101 101
101011 101 101 000 111 101 111 010 101 111
ANZAHL FREV: 3
101011 101001 101 101 000 111 101 111 010 010 111
ANZAHL FREV: 1
101100 001001 000 111 101 010 101 101 000 000 111
111001 111 101 111 101 101 000 000 000 010
ANZAHL FREV: 2
101101 001111 000 111 111 111 101 111 101 111 111
ANZAHL FREV: 1
101110 001100 000 101 010 111 101 010 101 000 101
110011 111 000 000 101 101 010 010 111 111
ANZAHL FREV: 2
110000 000110 000 000 000 000 111 000 111 111 000
ANZAHL FREV: 1
110011 000010 000 000 111 000 111 000 000 111 000
110000 111 010 000 111 111 101 010 010 101
111111 111 101 000 111 111 010 101 101 010
ANZAHL FREV: 3
110100 010111 010 010 111 000 111 111 111 111 111
110100 111 010 111 111 111 101 101 010 101
ANZAHL FREV: 2
11010 001011 000 111 000 000 111 111 000 101 111
010011 010 010 000 000 111 111 000 101 111
101010 101 111 101 111 111 101 000 101 101
101011 101 101 000 000 111 111 000 101 111
110011 111 000 000 000 111 111 000 101 111
ANZAHL FREV: 5
110111 101000 101 111 000 101 111 000 010 010 101
101101 101 101 111 000 111 111 111 000 111
ANZAHL FREV: 2
111000 101111 101 101 111 000 111 111 111 111 111
111010 111 101 111 111 111 010 010 101 010
ANZAHL FREV: 2
111010 001001 000 111 000 000 111 111 000 010 111
010001 010 010 000 000 111 111 000 010 111
011001 010 111 010 111 111 010 000 010 010
101001 101 101 000 000 111 111 000 010 111
110001 111 000 000 000 111 111 000 010 111
ANZAHL FREV: 5
111011 010101 010 010 111 000 111 111 111 000 111
011111 010 111 000 010 111 000 101 101 010
ANZAHL FREV: 2
111100 000000 000 000 111 111 111 111 000 000 000
010110 010 000 010 101 111 000 111 111 101
011110 010 101 000 010 111 101 111 111 000
100110 101 010 000 101 111 010 111 111 000
100111 101 000 101 010 111 000 111 111 010
111000 111 111 111 000 111 000 000 000 000
ANZAHL FREV: 6
*** SUMME FREV: 074
5.5 Die Anzahl der Elemente in einer Zustandsklasse
Es wurde ein Programm für die EDVA aufgestellt, das eine
Abschätzung der Anzahl der Zustande in einer Klasse geben
soll.
Die Folge
(Ui)i=1,2,… = (ϕi(0,0,0)U0)i=1,2,…
wird ausgehend von U0=(0,0,0,…,0) berechnet.
Diese Folge ist reinperiodisch. Wenn in ihr das erste mal
der Zustand Ui=(0,0,0,…,0) auftritt, dann ist ein Zyklus
von ϕ(0,0,0), wenn man diese Ableitung als Permutation der
Menge
.
Dies widerspricht X1 ≠ Y1.
5.4. Fixpunkte bezüglich ϕ2
Mit Hilfe einer EDVA wurden Fixpunkt bezüglich ϕ2 berech-
net. Zu diesem Zweck wurde das System (1.6) in ein zur Pro
grammierung günstigeres System umgeformt, unter besonderer
Berücksichtigung der notwendigen Bedingung (N1).
Die Methode zur Lösung der Aufgabe bestand im Durchprobieren
von 212 Möglichkeiten für 12 freie Variablen. Es wurden 74
Fixpunkte erhalten. Darunter, wie es auch sein muß, alle
Fixpunkte der Abbildung ϕ, siehe Punkt 3.1.
Die Aufstellung der Fixpunkte kann man auf den folgenden
Seiten finden.
Dort bedeutet
PAR - das Parametertupel (u01, u02, s1, s2, r1, r2),
FREV - gewisse Freie Parameter, die man nicht berücksichtigen braucht,
U03 U06 … U27 - die Darstellung des Fixpunktes U = (u1, u2,…,u27),
ANZAHL FREV - die Anzahl der Fixpunkte für eine gegebenes PAR.
Das erhaltene Resultat zeigt, daß die Verteilung der Fixpunkte
ziemlich unregelmäßig ist, obwohl man auch einige Beziehungen
bemerken kann.
Erläuterung zum Wert PAR:
PAR 0 0 0 0 0 0
s11 s12 s21 s22 f1 f2
03.10.1973 PROJEKT:MODELLVERGLEICH PROGRAMM: S4057
PAR FREV U03 U06 U09 U12 U15 U18 U21 U24 U27
000000 000110 000 000 111 000 000 000 111 111 000
ANZAHL FREV: 1
000011 001011 000 111 111 111 000 000 000 111 111
110010 111 010 010 000 000 010 000 111 101
111011 111 101 101 000 000 101 000 111 010
ANZAHL FREV: 3
000101 111010 111 111 000 111 000 111 000 101 000
ANZAHL FREV: 1
000110 100110 101 010 111 101 000 010 111 101 000
101100 101 111 000 000 000 010 101 000 101
ANZAHL FREV: 2
000111 010010 010 000 010 000 000 010 000 111 101
ANZAHL FREV: 1
001001 011001 010 111 000 000 000 101 010 000 010
011100 010 101 111 010 000 101 111 010 000
ANZAHL FREV: 2
001010 111000 111 111 000 111 000 111 000 010 000
ANZAHL FREV: 1
001011 100011 101 000 101 000 000 101 000 111 010
ANZAHL FREV: 1
001111 001001 000 111 010 101 000 101 010 010 111
001111 000 111 101 010 000 010 101 101 111
ANZAHL FREV: 2
010000 100100 101 010 111 101 010 101 101 010 000
101010 101 111 010 000 010 101 010 101 101
ANZAHL FREV: 2
010001 010110 010 000 101 000 010 101 101 111 101
ANZAHL FREV: 1
010010 111010 111 111 000 111 010 000 010 111 000
ANZAHL FREV: 1
010011 010000 010 000 010 010 010 000 010 010 101
011110 010 101 111 010 010 010 101 101 000
111001 111 101 101 000 010 010 010 010 010
ANZAHL FREV: 3
011000 010111 010 010 000 111 010 111 101 101 111
ANZAHL FREV: 1
011000 010101 010 010 000 111 010 111 101 010 111
011101 010 111 010 000 010 010 101 010 010
101001 101 101 010 101 010 010 000 000 111
ANZAHL FREV: 3
011100 001001 000 111 010 101 010 010 000 000 111
110000 111 010 111 010 010 000 000 000 101
ANZAHL FREV: 2
011101 000001 000 010 101 111 010 101 010 000 010
110111 111 000 000 010 010 101 101 111 111
ANZAHL FREV: 2
011110 001011 000 111 111 111 010 111 010 111 111
ANZAHL FREV: 1
100000 011010 010 101 111 010 101 010 010 101 000
011101 010 111 101 000 101 010 101 010 010
ANZAHL FREV: 2
100001 111110 111 111 000 111 101 000 101 111 000
ANZAHL FREV: 1
100010 100011 101 000 010 000 101 010 010 111 010
ANZAHL FREV: 1
100011 100000 101 010 111 101 101 101 010 010 000
100111 101 000 101 101 101 000 101 101 010
110110 111 010 010 000 101 101 101 101 101
ANZAHL FREV: 3
100100 010001 010 010 101 010 101 101 000 000 111
101010 101 111 101 000 101 101 010 101 101
101011 101 101 000 111 101 111 010 101 111
ANZAHL FREV: 3
101011 101001 101 101 000 111 101 111 010 010 111
ANZAHL FREV: 1
101100 001001 000 111 101 010 101 101 000 000 111
111001 111 101 111 101 101 000 000 000 010
ANZAHL FREV: 2
101101 001111 000 111 111 111 101 111 101 111 111
ANZAHL FREV: 1
101110 001100 000 101 010 111 101 010 101 000 101
110011 111 000 000 101 101 010 010 111 111
ANZAHL FREV: 2
110000 000110 000 000 000 000 111 000 111 111 000
ANZAHL FREV: 1
110011 000010 000 000 111 000 111 000 000 111 000
110000 111 010 000 111 111 101 010 010 101
111111 111 101 000 111 111 010 101 101 010
ANZAHL FREV: 3
110100 010111 010 010 111 000 111 111 111 111 111
110100 111 010 111 111 111 101 101 010 101
ANZAHL FREV: 2
11010 001011 000 111 000 000 111 111 000 101 111
010011 010 010 000 000 111 111 000 101 111
101010 101 111 101 111 111 101 000 101 101
101011 101 101 000 000 111 111 000 101 111
110011 111 000 000 000 111 111 000 101 111
ANZAHL FREV: 5
110111 101000 101 111 000 101 111 000 010 010 101
101101 101 101 111 000 111 111 111 000 111
ANZAHL FREV: 2
111000 101111 101 101 111 000 111 111 111 111 111
111010 111 101 111 111 111 010 010 101 010
ANZAHL FREV: 2
111010 001001 000 111 000 000 111 111 000 010 111
010001 010 010 000 000 111 111 000 010 111
011001 010 111 010 111 111 010 000 010 010
101001 101 101 000 000 111 111 000 010 111
110001 111 000 000 000 111 111 000 010 111
ANZAHL FREV: 5
111011 010101 010 010 111 000 111 111 111 000 111
011111 010 111 000 010 111 000 101 101 010
ANZAHL FREV: 2
111100 000000 000 000 111 111 111 111 000 000 000
010110 010 000 010 101 111 000 111 111 101
011110 010 101 000 010 111 101 111 111 000
100110 101 010 000 101 111 010 111 111 000
100111 101 000 101 010 111 000 111 111 010
111000 111 111 111 000 111 000 000 000 000
ANZAHL FREV: 6
*** SUMME FREV: 074
5.5 Die Anzahl der Elemente in einer Zustandsklasse
Es wurde ein Programm für die EDVA aufgestellt, das eine
Abschätzung der Anzahl der Zustande in einer Klasse geben
soll.
Die Folge
(Ui)i=1,2,… = (ϕi(0,0,0)U0)i=1,2,…
wird ausgehend von U0=(0,0,0,…,0) berechnet.
Diese Folge ist reinperiodisch. Wenn in ihr das erste mal
der Zustand Ui=(0,0,0,…,0) auftritt, dann ist ein Zyklus
von ϕ(0,0,0), wenn man diese Ableitung als Permutation der
Menge  betrachtet, durchlaufen.
Die Klasse enthält in diesem Falle nicht weniger als i Elemente.
Um irgend eine Kontrolle über die Richtigkeit der Rechnung zu
haben, werden sämtliche Ui ausgegeben, welche einem
von fünf im voraus gegebenen Fixpunkten sind oder die
(5.11)
U
betrachtet, durchlaufen.
Die Klasse enthält in diesem Falle nicht weniger als i Elemente.
Um irgend eine Kontrolle über die Richtigkeit der Rechnung zu
haben, werden sämtliche Ui ausgegeben, welche einem
von fünf im voraus gegebenen Fixpunkten sind oder die
(5.11)
U = U
= U = … = U
= … = U = 0
genügen.
Bis zum 10. Oktober 1973 wurde nach 35 Stunden Rechenzeit
i ≈ 27,7 * 106 erreicht, ohne den Zyklus zu beenden; es
wurden 2 Fixpunkte und 26 Werte, die (5.11) genügen
durchlaufen.
Daraus folgt:
Es existiert eine Zustandsklasse, die ≈ 27,7 * 106
oder mehr Elemente enthält.
§2 Determiniertes Chiffratormodell
1. Definition von Abbildungen
Bezeichnungen:
= 0
genügen.
Bis zum 10. Oktober 1973 wurde nach 35 Stunden Rechenzeit
i ≈ 27,7 * 106 erreicht, ohne den Zyklus zu beenden; es
wurden 2 Fixpunkte und 26 Werte, die (5.11) genügen
durchlaufen.
Daraus folgt:
Es existiert eine Zustandsklasse, die ≈ 27,7 * 106
oder mehr Elemente enthält.
§2 Determiniertes Chiffratormodell
1. Definition von Abbildungen
Bezeichnungen:
 = {0,1}208,
= {0,1}208,  = {0,1}52.
Ein Element S ∈
= {0,1}52.
Ein Element S ∈  hat folgende Gestalt
S = ((s
hat folgende Gestalt
S = ((s ,s
,s ),(s
),(s ,s
,s ), …,(s
), …,(s ,s
,s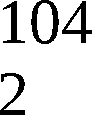 )).
Wenn für S ∈
)).
Wenn für S ∈  für k = 1,2 gilt
für k = 1,2 gilt
 dann sind diese S Elemente der Teilmenge
dann sind diese S Elemente der Teilmenge  der Menge
der Menge  .
Die Tupel (s
.
Die Tupel (s )
) werden rekurrent nach der Formel
s
werden rekurrent nach der Formel
s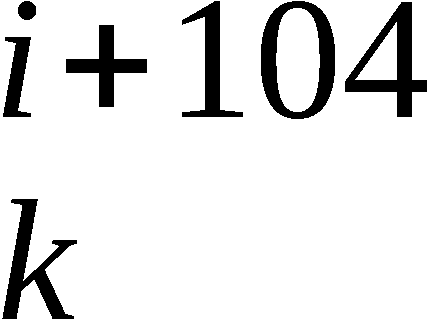 s
s (k = 1,2; i = 1,2,…) fortgesetzt.
Das Tupel F =(fi)
(k = 1,2; i = 1,2,…) fortgesetzt.
Das Tupel F =(fi) wird rekurrent nach der
Formel fi+52 = fi+3 + fi (i = 1,2,…)
fortgesetzt.
Mit
wird rekurrent nach der
Formel fi+52 = fi+3 + fi (i = 1,2,…)
fortgesetzt.
Mit  bezeichnen wir die Menge aller F ∈
bezeichnen wir die Menge aller F ∈  außer
F = (0,0,0,….,0).
Die Folge (ri)i=1,2,… wird durch die Formel
rk+10ö = rk+52+104l = fП(k)+l (k=1,52; l=0,1,2,…);
definiert, wobei П(k) folgende Permutation ist
außer
F = (0,0,0,….,0).
Die Folge (ri)i=1,2,… wird durch die Formel
rk+10ö = rk+52+104l = fП(k)+l (k=1,52; l=0,1,2,…);
definiert, wobei П(k) folgende Permutation ist
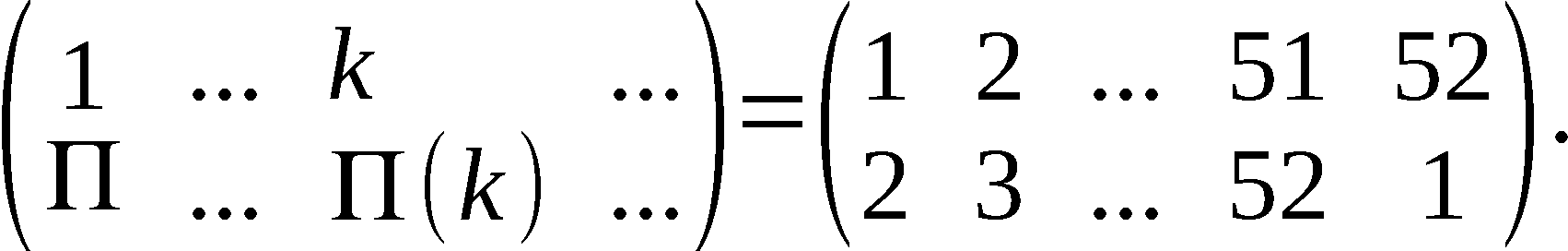 Schließlich führen wir noch folgende Bezeichnungen ein:
Schließlich führen wir noch folgende Bezeichnungen ein:
 ={0,1}∞,
={0,1}∞,  L
L - sei eine beliebige natürliche Zahl.
Wir können die Abbildung Ψ der Menge
L
L - sei eine beliebige natürliche Zahl.
Wir können die Abbildung Ψ der Menge  x
x x
x  in
in und die Abbildung ΨL der Menge
und die Abbildung ΨL der Menge  x
x  x
x  in
in  L
auf folgende Art definieren:
Ausgehend von einem U = U0 ∈
L
auf folgende Art definieren:
Ausgehend von einem U = U0 ∈  wird die Folge
(Ui)i=1,2,…
mit Hilfe der Abbildung ϕ (siehe §1) nach der Formel
Ui = ϕ(s
wird die Folge
(Ui)i=1,2,…
mit Hilfe der Abbildung ϕ (siehe §1) nach der Formel
Ui = ϕ(s ,s
,s ,ri)Ui-1
gebildet, wobei (P,R) fest seien.
Sei ϕ ein fester Index aus dem Bereich 1,27. Wir setzen
u
,ri)Ui-1
gebildet, wobei (P,R) fest seien.
Sei ϕ ein fester Index aus dem Bereich 1,27. Wir setzen
u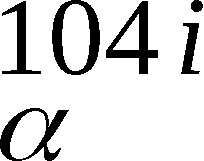 = ai (i=1,2,…)
(ai)i=1,2,… = A,
(ai)
= ai (i=1,2,…)
(ai)i=1,2,… = A,
(ai) = AL.
Dann gilt
A = Ψ(U,S,F) , AL = ΨL(U,S,F).
Wir bezeichnen mit A die Menge aller Elemente A ∈
= AL.
Dann gilt
A = Ψ(U,S,F) , AL = ΨL(U,S,F).
Wir bezeichnen mit A die Menge aller Elemente A ∈  , die wir
erhalten, wenn (U,S,F) die Menge
, die wir
erhalten, wenn (U,S,F) die Menge  x
x  x
x  durchläuft;
durchläuft;
 L erhalten wir entsprechend.
ΨL :
L erhalten wir entsprechend.
ΨL :  x
x  x
x  →
→  L
L 
 L (L = 1,2,…)
Symbolisch:
L (L = 1,2,…)
Symbolisch:
 = Ψ(
= Ψ( ,
, ) ,
) ,  L=ΨL(
L=ΨL( ,
, ).
Desweiteren werden wir auch manchmal die Abbildung Φ
der Menge
).
Desweiteren werden wir auch manchmal die Abbildung Φ
der Menge  in sich benutzen;
Φ(S,F)U = U104 = ϕ(s
in sich benutzen;
Φ(S,F)U = U104 = ϕ(s ,s
,s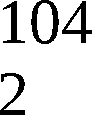 ,r104) … ϕ(s
,r104) … ϕ(s ,s
,s ,r1)U.
Manchmal ist es zweckmäßig, mit Ui(U0),S,F) die Abhängigkeit
von Ui = ϕ(s
,r1)U.
Manchmal ist es zweckmäßig, mit Ui(U0),S,F) die Abhängigkeit
von Ui = ϕ(s ,s
,s ,ri) … ϕ(s
,ri) … ϕ(s ,s
,s ,r1)U0 von U0,S,F zu
kennzeichnen.
Im gesamten Paragraphen sei stets (P,R) ∈ P,R, obwohl diese
Einschränkung nicht immer notwendig ist.
2. Kryptologische Interpretation und elementare
Eigenschaften der Abbildungen
2.1. Für L = 47 wird die Abbildung ΨL im Chiffrator des Systems
OPERATION in der derzeitigen Gestalt realisiert, siehe
Kapitel III. Dabei ist
,r1)U0 von U0,S,F zu
kennzeichnen.
Im gesamten Paragraphen sei stets (P,R) ∈ P,R, obwohl diese
Einschränkung nicht immer notwendig ist.
2. Kryptologische Interpretation und elementare
Eigenschaften der Abbildungen
2.1. Für L = 47 wird die Abbildung ΨL im Chiffrator des Systems
OPERATION in der derzeitigen Gestalt realisiert, siehe
Kapitel III. Dabei ist  die Schlüsselmenge;
für die weitere Untersuchungen betrachten wir manchmal
die Schlüsselmenge;
für die weitere Untersuchungen betrachten wir manchmal
 als Schlüsselmenge. Das Tupel F ist der Inhalt des
Registers SRF.
A47 ist die Additionsreihe. U0, α, P und R sind Lang-
zeitschlüssel, die als feststehend angenommen werden.
Im weiteren werden wir manchmal ΨL für allgemeines L
betrachten; in diesem Fall ist AL die Additionsreihe.
2.2. Infolge |
als Schlüsselmenge. Das Tupel F ist der Inhalt des
Registers SRF.
A47 ist die Additionsreihe. U0, α, P und R sind Lang-
zeitschlüssel, die als feststehend angenommen werden.
Im weiteren werden wir manchmal ΨL für allgemeines L
betrachten; in diesem Fall ist AL die Additionsreihe.
2.2. Infolge | | = 2198 ≈ 1060 ist der Schlüsselvorrat
gleich dieser Zahl.
Wenn der Schlüssel zweimal innerhalb von 24 Stunden gewech-
selt wird und gleichzeitig 20 Chiffriernetze arbeiten, dann
hat die Wahrscheinlichkeit dafür, daß in einem Jahr in allen
Netzen zusammengenommen kein Schlüssel zweimal verwendet
wird, die Ordnung 1-10-52.
Tatsächlich, wenn a = 2 * 20 * 365 ist, wird diese Wahr-
scheinlichkeit nach folgender Formel berechnet:
|
| = 2198 ≈ 1060 ist der Schlüsselvorrat
gleich dieser Zahl.
Wenn der Schlüssel zweimal innerhalb von 24 Stunden gewech-
selt wird und gleichzeitig 20 Chiffriernetze arbeiten, dann
hat die Wahrscheinlichkeit dafür, daß in einem Jahr in allen
Netzen zusammengenommen kein Schlüssel zweimal verwendet
wird, die Ordnung 1-10-52.
Tatsächlich, wenn a = 2 * 20 * 365 ist, wird diese Wahr-
scheinlichkeit nach folgender Formel berechnet:
| | * (|
| * (| |-1) * … * (|
|-1) * … * (| |-a+1) ≈ 1 - a2 ≈ 1-10-52
|
|-a+1) ≈ 1 - a2 ≈ 1-10-52
| |a 2(
|a 2( )
2.3 Die Zahl der Additionsreihen, die man theoretische mit
einem Schlüssel erzeugen kann, ist gleich
|
)
2.3 Die Zahl der Additionsreihen, die man theoretische mit
einem Schlüssel erzeugen kann, ist gleich
| | = 252-1 ≈ 1015.
Aus der Beschreibung des Chiffrators, siehe Kapitel II,
folgt, daß der Abstand zwischen aufeinanderfolgenden
Additionsreihen 77 Zeichen der Folge(fi)i oder mehr
beträgt. Deshalb kann man mit einem Schlüssel nicht mehr
als 1/77 (252-1) ≈ 5 * 1013 Additionsreihen erzeugen. In
24 Stunden werden bei maximaler Arbeitsgeschwindigkeit des
Chiffrators von 1200 Baud
1200 * 24 * 60 * 60 Zeichen (fi)i
abgearbeitet, d.h. b = 1/77 1200 * 24 * 60 * 60 ≈ 1060
Additionsreihen; diese Zahl verringert sich etwas, wenn
wir die Notwendigkeit der Synchronisation berücksichtigen.
Abstrahieren wir von der Realität und setzen die Elemente
F ∈
| = 252-1 ≈ 1015.
Aus der Beschreibung des Chiffrators, siehe Kapitel II,
folgt, daß der Abstand zwischen aufeinanderfolgenden
Additionsreihen 77 Zeichen der Folge(fi)i oder mehr
beträgt. Deshalb kann man mit einem Schlüssel nicht mehr
als 1/77 (252-1) ≈ 5 * 1013 Additionsreihen erzeugen. In
24 Stunden werden bei maximaler Arbeitsgeschwindigkeit des
Chiffrators von 1200 Baud
1200 * 24 * 60 * 60 Zeichen (fi)i
abgearbeitet, d.h. b = 1/77 1200 * 24 * 60 * 60 ≈ 1060
Additionsreihen; diese Zahl verringert sich etwas, wenn
wir die Notwendigkeit der Synchronisation berücksichtigen.
Abstrahieren wir von der Realität und setzen die Elemente
F ∈  für die Erzeugung der Additionsreihe als zufällig
gewählt voraus.
Wir setzen weiter voraus, daß alle 247 möglichen Additions-
reihen gleich häufig entstehen, d. h. 25 = 32 Mal, wenn F
die ganze Menge
für die Erzeugung der Additionsreihe als zufällig
gewählt voraus.
Wir setzen weiter voraus, daß alle 247 möglichen Additions-
reihen gleich häufig entstehen, d. h. 25 = 32 Mal, wenn F
die ganze Menge  durchläuft.
Dann ist die Wahrscheinlichkeit dafür, daß alle in 24 Stun-
den erhaltenen Additionsreihen paarweise verschieden sind,
analog zum vorigen Punkt
≈ 1 - 32 * 62 ≈ 0,98.
|
durchläuft.
Dann ist die Wahrscheinlichkeit dafür, daß alle in 24 Stun-
den erhaltenen Additionsreihen paarweise verschieden sind,
analog zum vorigen Punkt
≈ 1 - 32 * 62 ≈ 0,98.
| | 2
Dieses Resultat weist daraufhin, daß es in der Praxis
in einzelnen Fällen vorkommen kann, daß es im Geltungs-
zeitraum ein- und desselben Schlüssels zwei Klartexte gibt,
die, bei verschiedenen F, mit ein- und der selben Additions-
reihe chiffriert werden.
Erst recht kann es vorkommen, daß zwei Additionsreihen
phasengleich sind.
2.4 Die Abbildung Φ, Ψ und ΨL sind offensichtlich eindeutig.
Für feste S und F ist Φ(S,F) eineindeutig auf
| 2
Dieses Resultat weist daraufhin, daß es in der Praxis
in einzelnen Fällen vorkommen kann, daß es im Geltungs-
zeitraum ein- und desselben Schlüssels zwei Klartexte gibt,
die, bei verschiedenen F, mit ein- und der selben Additions-
reihe chiffriert werden.
Erst recht kann es vorkommen, daß zwei Additionsreihen
phasengleich sind.
2.4 Die Abbildung Φ, Ψ und ΨL sind offensichtlich eindeutig.
Für feste S und F ist Φ(S,F) eineindeutig auf  genau dann,
wenn (P,R) ∈ P,R.
Kann dieselbe Folge (Ui)i=1,2, … durch verschiedene
(U0,S,F) ∈
genau dann,
wenn (P,R) ∈ P,R.
Kann dieselbe Folge (Ui)i=1,2, … durch verschiedene
(U0,S,F) ∈  x
x  x
x  entstehen?
Mögen (U,S,F) und (U',S',F') dieselbe Folge (Ui)i=1,2,…
erzeugen. Wir haben
U1 = ϕ(s
entstehen?
Mögen (U,S,F) und (U',S',F') dieselbe Folge (Ui)i=1,2,…
erzeugen. Wir haben
U1 = ϕ(s ,s
,s ,r1)U = ϕ(s
,r1)U = ϕ(s ',s
',s ',r1')U'.
Für U = U' erhält man aufgrund der Eineindeutigkeit von ϕ
s
',r1')U'.
Für U = U' erhält man aufgrund der Eineindeutigkeit von ϕ
s = s
= s ', s
', s = s
= s ', r1 = r1'.
Analog erhält man aus der Betrachtung U2, U3, …
S = S' und F = F'.
Für U ≠ U' muß (s
', r1 = r1'.
Analog erhält man aus der Betrachtung U2, U3, …
S = S' und F = F'.
Für U ≠ U' muß (s , s
, s ,r1) ≠ (s
,r1) ≠ (s ', s
', s ', r1') sein.
Aber aus der Betrachtung von U2, U3, … erhält man
(s
', r1') sein.
Aber aus der Betrachtung von U2, U3, … erhält man
(s , s
, s ,ri) = (s
,ri) = (s ', s
', s ', ri') für i = 2,3,…
und somit: Für festes U0 besteht eine eineindeutige
Zuordnung zwischen
', ri') für i = 2,3,…
und somit: Für festes U0 besteht eine eineindeutige
Zuordnung zwischen  x
x  und der Gesamtheit der
Folgen (Ui)i=1,2, …
Für U0 ≠ U0' können die Folgen (Ui)i=1,2,… bzw. (Ui')i=1,2,…
genau dann übereinstimmen, wenn U0' ∈ {ϕ-1ϕU0}.
Die Menge {ϕ-1ϕU} wird im §1, Punkt 4, untersucht.
2.5. Im §1, Punkt 4, wurden die Zustandsklassen der Abbildung ϕ
definiert:
und der Gesamtheit der
Folgen (Ui)i=1,2, …
Für U0 ≠ U0' können die Folgen (Ui)i=1,2,… bzw. (Ui')i=1,2,…
genau dann übereinstimmen, wenn U0' ∈ {ϕ-1ϕU0}.
Die Menge {ϕ-1ϕU} wird im §1, Punkt 4, untersucht.
2.5. Im §1, Punkt 4, wurden die Zustandsklassen der Abbildung ϕ
definiert:
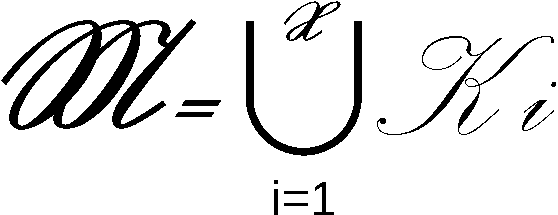 , i ≠ j :
, i ≠ j : Analog kann man die Zustandsklassen von Φ definieren,
wobei S ∈
Analog kann man die Zustandsklassen von Φ definieren,
wobei S ∈  und F ∈
und F ∈  zugelassen werden:
zugelassen werden:
 , i ≠ j :
, i ≠ j :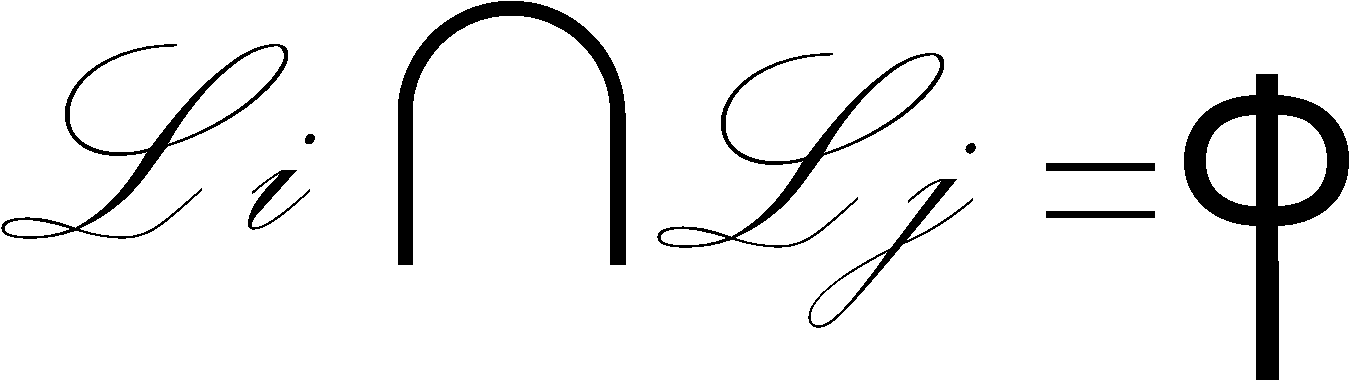 Dann ist leicht zu sehen, daß
Dann ist leicht zu sehen, daß  gilt, und jede Klasse
Ki zerfällt in (eine oder mehrere) Klassen
gilt, und jede Klasse
Ki zerfällt in (eine oder mehrere) Klassen  i1,
i1,  i2, …
Aufgrund dessen, daß Φ das Produkt mehrerer ϕ ist, folgt
aus v ≡ u (mod
i2, …
Aufgrund dessen, daß Φ das Produkt mehrerer ϕ ist, folgt
aus v ≡ u (mod  ) v ≡ u (mod K), aber die Umkehrung gilt
nicht unbedingt, da Φ nicht alle möglichen Produkte von ϕ
einschließt.
(Die Schreibweise v ≡ u (mod …) bedeutet, daß v ∈
) v ≡ u (mod K), aber die Umkehrung gilt
nicht unbedingt, da Φ nicht alle möglichen Produkte von ϕ
einschließt.
(Die Schreibweise v ≡ u (mod …) bedeutet, daß v ∈  und
u ∈
und
u ∈  zu einer Klasse von Φ bzw. ϕ gehören).
2.6 Wir zeigen, daß bei festen S ∈
zu einer Klasse von Φ bzw. ϕ gehören).
2.6 Wir zeigen, daß bei festen S ∈  und U0 ∈
und U0 ∈  eine
eineindeutige Zuordnung zwischen
eine
eineindeutige Zuordnung zwischen  und der Gesamtheit
der Folgen (Ui)i=1,2,…, sowie zwischen
und der Gesamtheit
der Folgen (Ui)i=1,2,…, sowie zwischen  und der
Gesamtheit der Folgen (
und der
Gesamtheit der Folgen ( )i=1,2,… bei festen α ∈ 1,57
besteht.
Die erste Behauptung folgt aus den Ergebnissen des Punktes 2.4.
Beweisen wir die zweite Behauptung.
Seien F = (f1,f2,…,f52) ∈
)i=1,2,… bei festen α ∈ 1,57
besteht.
Die erste Behauptung folgt aus den Ergebnissen des Punktes 2.4.
Beweisen wir die zweite Behauptung.
Seien F = (f1,f2,…,f52) ∈  ,
F1 = (f
,
F1 = (f ,f
,f , …,f
, …,f ) ∈
) ∈  , F≠F1
k - der kleinste Index, bei dem sich F und F1
voneinander unterscheiden (k ∈ 1,52),
α = 3ɳ-2, ɳ ∈ 1,9.
Offenbar ist dann Ui(F) = Ui(F1) für i < K,
u
, F≠F1
k - der kleinste Index, bei dem sich F und F1
voneinander unterscheiden (k ∈ 1,52),
α = 3ɳ-2, ɳ ∈ 1,9.
Offenbar ist dann Ui(F) = Ui(F1) für i < K,
u (F) = u
(F) = u + fK + sK∆ɳ + Tɳ(sK,u
+ fK + sK∆ɳ + Tɳ(sK,u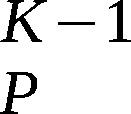 )
u
)
u (F1) = u
(F1) = u + f
+ f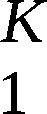 + sK∆ɳ + Tɳ(sK,u
+ sK∆ɳ + Tɳ(sK,u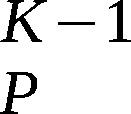 ).
Wegen fK ≠ f
).
Wegen fK ≠ f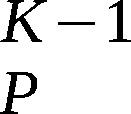 ergibt sich u
ergibt sich u (F) ≠ u
(F) ≠ u (F1).
Der Fall α ≠ 3ɳ-2 erfordert keine besondere Betrachtung
wegen 2Ui = 1Ui+1 = 0Ui+2.
3. Periodizitätseigenschaften
3.1 Periodizität von Folgen
Eine endliche oder unendliche Folge
g = (gi)i=1,2,…, gi ∈ A, wobei A irgendeine endliche
Menge ist, heißt periodisch (genauer: reinperiodisch),
wenn eine natürliche Zahl D existiert, so daß
gi+D = gi für alle i=1,2,…
Die Zahl D nennen wir Periode der Folge g. Wenn D Periode
ist, so ist ein beliebiges Vielfaches der Zahl D ebenfalls
Periode. Die kleinste Periode nennen wir Minimalperiode und
bezeichnen sie mit d.
Die Minimalperiode ist Teiler jeder beliebigen anderen
(3.1)
Periode: d/D.
(Wenn a und b natürliche Zahlen sind, so bedeuten a/b, daß
a Teiler von b ist, und a
(F1).
Der Fall α ≠ 3ɳ-2 erfordert keine besondere Betrachtung
wegen 2Ui = 1Ui+1 = 0Ui+2.
3. Periodizitätseigenschaften
3.1 Periodizität von Folgen
Eine endliche oder unendliche Folge
g = (gi)i=1,2,…, gi ∈ A, wobei A irgendeine endliche
Menge ist, heißt periodisch (genauer: reinperiodisch),
wenn eine natürliche Zahl D existiert, so daß
gi+D = gi für alle i=1,2,…
Die Zahl D nennen wir Periode der Folge g. Wenn D Periode
ist, so ist ein beliebiges Vielfaches der Zahl D ebenfalls
Periode. Die kleinste Periode nennen wir Minimalperiode und
bezeichnen sie mit d.
Die Minimalperiode ist Teiler jeder beliebigen anderen
(3.1)
Periode: d/D.
(Wenn a und b natürliche Zahlen sind, so bedeuten a/b, daß
a Teiler von b ist, und a 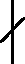 b bedeutet das Gegenteil.)
In der Tat,
sei d
b bedeutet das Gegenteil.)
In der Tat,
sei d 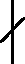 D. Dann existiert eine natürliche Zahl A, 0 < A < d,
mit der Eigenschaft d/D + A. Aber da D + A = nd, gilt
gi = gi+nd = gi+D+A = gi+A für alle i,
was der Definition der Minimalperiode d widerspricht.
(Diese Definition der Minimalperiode ist allgemein bekannt.)
Wenn g nur ab i0 > 1 reinperiodisch ist, so heißt der Teil
(g1,g2,…,gi0-1) der Folge g Vorperiode der Länge
i0-1, und die Folge selbst heißt periodisch mit Vorperiode.
Zur Bezeichnung der Minimalperiode der Folge g verwenden wir
im weiteren die Bezeichnung
d = d <g>.
Sei die Folge h = (hi)i=1,2,… aus g nach der Formel
hi = gni gebildet, wobei n eine beliebige fest natürliche
Zahl ist. Dann ist d <g> Periode von h:
hi+d = gni+nd = gni = hi,
(3.2)
und nach (3.1) d<h> | <g>.
Wenn g reinperiodisch ist, so ist auch h reinperiodisch.
3.2 Die Periode der Folge r
Aus der Literatur ist bekannt, daß für f = (fi)i=1,2,…
gilt d>f< = d0 = s52-1.
Die Folge r = (ri)i=1,2,… hat die Periode e = 104d0.
Das ist durch wiederholte Anwendung der Definition von
r leicht zu sehen;
k = 1,52; l = 0,1,2,…
rk+104l+e = rk+52+104l+e = fΠ(k)+l+d0 = fΠ(k)+l = rk+104l = rk+52+104l
Theorem:
(3.3) d <r> = 104 * (252-1)
Beweis:
Sei S < 104 d0 Periode von r.
Dann kann man δ folgendermaßen darstellen
δ = 104 a+b, 0 ≤ a < d0, 0 ≤ b < 104.
Sei 52/δ. dann gilt b = 0 oder b = 52 und man kann für alle
k = 1,52 und l = 0,1,2,… schreiben
fΠ(k)+l = rk+104l = rk+104(l+a)+b fΠ(k)+l+a,
was a < d0 widerspricht.
Sei 0 < b < 52. Wir betrachten die Gleichung ri = ri+104a+b
für i = 104j + 52 und für i = 104j + 104 (j=0,1,2,…).
Dann erhalten wir aus der Definition von r
fΠ(52)+j = fΠ(b)+j+a
fΠ(52)+j = fΠ(b)+1+j+a
das heißt
fΠ(b)+a = fΠ(b)+a+1 = fΠ(b)+a+2 = …,
was unmöglich ist.
Für 52 < b < 104 erhält man ein analoges Resultat, wenn man
i = 104j+1 und i = 104j+53 betrachtet.
3.3 Die Periode der Folge (Ui)i=0,1,2,…
Seien (P,R) ∈ P,R, U0 ∈
D. Dann existiert eine natürliche Zahl A, 0 < A < d,
mit der Eigenschaft d/D + A. Aber da D + A = nd, gilt
gi = gi+nd = gi+D+A = gi+A für alle i,
was der Definition der Minimalperiode d widerspricht.
(Diese Definition der Minimalperiode ist allgemein bekannt.)
Wenn g nur ab i0 > 1 reinperiodisch ist, so heißt der Teil
(g1,g2,…,gi0-1) der Folge g Vorperiode der Länge
i0-1, und die Folge selbst heißt periodisch mit Vorperiode.
Zur Bezeichnung der Minimalperiode der Folge g verwenden wir
im weiteren die Bezeichnung
d = d <g>.
Sei die Folge h = (hi)i=1,2,… aus g nach der Formel
hi = gni gebildet, wobei n eine beliebige fest natürliche
Zahl ist. Dann ist d <g> Periode von h:
hi+d = gni+nd = gni = hi,
(3.2)
und nach (3.1) d<h> | <g>.
Wenn g reinperiodisch ist, so ist auch h reinperiodisch.
3.2 Die Periode der Folge r
Aus der Literatur ist bekannt, daß für f = (fi)i=1,2,…
gilt d>f< = d0 = s52-1.
Die Folge r = (ri)i=1,2,… hat die Periode e = 104d0.
Das ist durch wiederholte Anwendung der Definition von
r leicht zu sehen;
k = 1,52; l = 0,1,2,…
rk+104l+e = rk+52+104l+e = fΠ(k)+l+d0 = fΠ(k)+l = rk+104l = rk+52+104l
Theorem:
(3.3) d <r> = 104 * (252-1)
Beweis:
Sei S < 104 d0 Periode von r.
Dann kann man δ folgendermaßen darstellen
δ = 104 a+b, 0 ≤ a < d0, 0 ≤ b < 104.
Sei 52/δ. dann gilt b = 0 oder b = 52 und man kann für alle
k = 1,52 und l = 0,1,2,… schreiben
fΠ(k)+l = rk+104l = rk+104(l+a)+b fΠ(k)+l+a,
was a < d0 widerspricht.
Sei 0 < b < 52. Wir betrachten die Gleichung ri = ri+104a+b
für i = 104j + 52 und für i = 104j + 104 (j=0,1,2,…).
Dann erhalten wir aus der Definition von r
fΠ(52)+j = fΠ(b)+j+a
fΠ(52)+j = fΠ(b)+1+j+a
das heißt
fΠ(b)+a = fΠ(b)+a+1 = fΠ(b)+a+2 = …,
was unmöglich ist.
Für 52 < b < 104 erhält man ein analoges Resultat, wenn man
i = 104j+1 und i = 104j+53 betrachtet.
3.3 Die Periode der Folge (Ui)i=0,1,2,…
Seien (P,R) ∈ P,R, U0 ∈  , S ∈
, S ∈  , F ∈
, F ∈  fest.
Es gilt
(3.4)
d < (s
fest.
Es gilt
(3.4)
d < (s ,s
,s ,ri)i=1,2,… > / 104 * (252-1)
Tatsächlich, diese Zahl fällt zusammen mit d<r> = e
und d < (s
,ri)i=1,2,… > / 104 * (252-1)
Tatsächlich, diese Zahl fällt zusammen mit d<r> = e
und d < (s )i=1,2,… > / 104 für k = 1,2.
Das heißt, wenn wir bezeichnen ϕi = ϕ(s
)i=1,2,… > / 104 für k = 1,2.
Das heißt, wenn wir bezeichnen ϕi = ϕ(s ,
, ,ri), so gilt
d < (ϕi)i=1,2,… e und ϕi = ϕi+e für i=1,2,…
Aufgrund der Endlichkeit der Menge
,ri), so gilt
d < (ϕi)i=1,2,… e und ϕi = ϕi+e für i=1,2,…
Aufgrund der Endlichkeit der Menge  existieren natür-
liche Zahlen j1 und j2 > j1 derart, daß
Uj1e = Uj2e, j2 ≤ j1 + 227.
Indem wir ϕ1 = ϕ1+j1e = ϕ1+j2e berücksichtigen, folgt
Uj1e+1 = ϕ1+j1e, Uj1e = ϕ1+j2e, Uj2e = Uj2e+1 usw.
Deshalb ist (Ui)i periodisch, wobei die
existieren natür-
liche Zahlen j1 und j2 > j1 derart, daß
Uj1e = Uj2e, j2 ≤ j1 + 227.
Indem wir ϕ1 = ϕ1+j1e = ϕ1+j2e berücksichtigen, folgt
Uj1e+1 = ϕ1+j1e, Uj1e = ϕ1+j2e, Uj2e = Uj2e+1 usw.
Deshalb ist (Ui)i periodisch, wobei die  Periode ein
Vielfaches der Zahl e und nicht größer als 227e ist.
Angenommen, die Folge habe eine Vorperiode der Länge n
und die Periode me:
(Ui)i = U0, U1, …, Un-1, Un, Un+1,…, Un+me-1, Un, Un+1,…
Unter dieser Voraussetzung muß gelten
Un-1 ≠ Un+me-1
Aber aus der Gleichung
Un = ϕn+meUn+me = ϕnUn+me-1 = ϕnUn-1
folgt aufgrund der Eineindeutigkeit von ϕ ein Widerspruch.
Deshalb ist (Ui)i reinperiodisch.
Wir bezeichnen p = d (Ui)i = 0,1,….
Die Komponentenfolge (
Periode ein
Vielfaches der Zahl e und nicht größer als 227e ist.
Angenommen, die Folge habe eine Vorperiode der Länge n
und die Periode me:
(Ui)i = U0, U1, …, Un-1, Un, Un+1,…, Un+me-1, Un, Un+1,…
Unter dieser Voraussetzung muß gelten
Un-1 ≠ Un+me-1
Aber aus der Gleichung
Un = ϕn+meUn+me = ϕnUn+me-1 = ϕnUn-1
folgt aufgrund der Eineindeutigkeit von ϕ ein Widerspruch.
Deshalb ist (Ui)i reinperiodisch.
Wir bezeichnen p = d (Ui)i = 0,1,….
Die Komponentenfolge ( )i=0,1,… mit α = 1,27 sind rein-
periodisch mit der Periode p. Nach Definition ϕ gilt
u
)i=0,1,… mit α = 1,27 sind rein-
periodisch mit der Periode p. Nach Definition ϕ gilt
u = u
= u + ri
u
+ ri
u = u
= u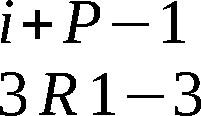 + ri+P
Indem wir beide Gleichungen addieren, erhalten wir
ri = ri+p i = 1,2,…
Hieraus folgt aufgrund von (3.3) p > e, e | p.
Die erhaltenen Resultate führen uns zu folgendem Theorem:
Theorem:
Die Folge (Ui)i=0,1,… ist reinperiodisch.
Sei p ihre Minimalperiode. Dann gilt
(3.5)
p = K * 104 * (252-1),
wobei K eine natürliche Zahl aus dem Abschnitt 1,227 ist.
Bemerkung:
Infolge (3.2) dar man hieraus nicht auf
d < (U104i)i=0,1,… | d (U1)
schließen.
Wegen (3.5) muß man darauf schließen.
3.4 Die Periode der Folge (
+ ri+P
Indem wir beide Gleichungen addieren, erhalten wir
ri = ri+p i = 1,2,…
Hieraus folgt aufgrund von (3.3) p > e, e | p.
Die erhaltenen Resultate führen uns zu folgendem Theorem:
Theorem:
Die Folge (Ui)i=0,1,… ist reinperiodisch.
Sei p ihre Minimalperiode. Dann gilt
(3.5)
p = K * 104 * (252-1),
wobei K eine natürliche Zahl aus dem Abschnitt 1,227 ist.
Bemerkung:
Infolge (3.2) dar man hieraus nicht auf
d < (U104i)i=0,1,… | d (U1)
schließen.
Wegen (3.5) muß man darauf schließen.
3.4 Die Periode der Folge ( )i=0,1,…
Da (Ui)i reinperiodisch ist, ist jede Komponentenfolge
(
)i=0,1,…
Da (Ui)i reinperiodisch ist, ist jede Komponentenfolge
( )i reinperiodisch
Jede Periode von (Ui)i ist offensichtlich für jedes
α ∈ 1,27 Periode von (Ui)i.
Indem man Pα = d < (Ui)i=0,1,… > bezeichnet, kann man auf-
grund von(3.1) folgende Ungleichung aufstellen
(3.6)
Pα ≤P, α = 1,27
(3.7)
Da u
)i reinperiodisch
Jede Periode von (Ui)i ist offensichtlich für jedes
α ∈ 1,27 Periode von (Ui)i.
Indem man Pα = d < (Ui)i=0,1,… > bezeichnet, kann man auf-
grund von(3.1) folgende Ungleichung aufstellen
(3.6)
Pα ≤P, α = 1,27
(3.7)
Da u = u
= u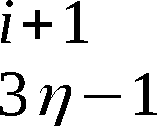 = u
= u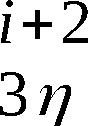 gilt
P3ɳ-2 = P3ɳ-1 = P3ɳ, ɳ = 1,9
Die Folge (u
gilt
P3ɳ-2 = P3ɳ-1 = P3ɳ, ɳ = 1,9
Die Folge (u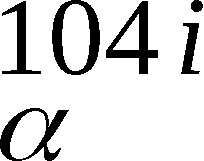 )i ist reinperiodisch;
aufgrund von (3.2) und (3.6) gilt
(3.8)
α < (u
)i ist reinperiodisch;
aufgrund von (3.2) und (3.6) gilt
(3.8)
α < (u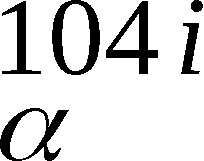 )i | P
4. Analytische Abhängigkeiten
Mit der Formel (§1, 1.1) wird die Abbildung durch lo-
gische Funktionen definiert.
Analog kann man jedes Element
)i | P
4. Analytische Abhängigkeiten
Mit der Formel (§1, 1.1) wird die Abbildung durch lo-
gische Funktionen definiert.
Analog kann man jedes Element  als logische Funktion
darstellen, deren Argumente die 287 Komponenten der Größen
U0, S und F sind:
als logische Funktion
darstellen, deren Argumente die 287 Komponenten der Größen
U0, S und F sind:
 =
=  (U0), S, F) = h
(U0), S, F) = h (u
(u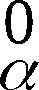 ,…,s
,…,s ,…,s
,…,s ,…,f1,…,f52).
In der Gesamtheit dieser Funktionen für α = 1,27 und
i = 1,2,… ist die vollständige Information über die kryp-
tologische Schaltung enthalten. Das heißt, man kann in der
Sprache dieser Funktionen alle zu untersuchenden Aufgaben
formulieren und zu lösen versuchen. Bereits die Anzahl der
Argumente der Funktion h
,…,f1,…,f52).
In der Gesamtheit dieser Funktionen für α = 1,27 und
i = 1,2,… ist die vollständige Information über die kryp-
tologische Schaltung enthalten. Das heißt, man kann in der
Sprache dieser Funktionen alle zu untersuchenden Aufgaben
formulieren und zu lösen versuchen. Bereits die Anzahl der
Argumente der Funktion h weist darauf hin, daß man ihren
expliziten Ausdruck für außerordentlich umfangreich halten
muß, und es schwerlich gelingen wird, damit fertig zu werden.
Das ist aus kryptologischer Sicht nicht schlecht, aber
erschwert die analytische Untersuchung.
Wegen der Determiniertheit und der vollständigen Definiert-
heit der kryptologischen Schaltung kann man die Berechnung
von h
weist darauf hin, daß man ihren
expliziten Ausdruck für außerordentlich umfangreich halten
muß, und es schwerlich gelingen wird, damit fertig zu werden.
Das ist aus kryptologischer Sicht nicht schlecht, aber
erschwert die analytische Untersuchung.
Wegen der Determiniertheit und der vollständigen Definiert-
heit der kryptologischen Schaltung kann man die Berechnung
von h vollständig formalisieren und somit einer EDVA
übergeben.
Dasselbe gilt für das Auffinden vieler Eigenschaften
von h
vollständig formalisieren und somit einer EDVA
übergeben.
Dasselbe gilt für das Auffinden vieler Eigenschaften
von h , zum Beispiel das Finden der Anzahl der
effektiven Argumente.
Ein Argument einer logischen Funktion heißt effektiv, falls
die Funktion effektiv von ihm abhängt. Zum Beispiel können
fi+1, fi+2, … ,fi+52
nach der Definition von
, zum Beispiel das Finden der Anzahl der
effektiven Argumente.
Ein Argument einer logischen Funktion heißt effektiv, falls
die Funktion effektiv von ihm abhängt. Zum Beispiel können
fi+1, fi+2, … ,fi+52
nach der Definition von  nicht effektive Argumente der
logischen Funktion h
nicht effektive Argumente der
logischen Funktion h mit i < 52, α ∈ 1,27 sein.
Eine beliebige logische Funktion kann man als Summe (mod 2)
von Produkten der Argumente darstellen:
h
mit i < 52, α ∈ 1,27 sein.
Eine beliebige logische Funktion kann man als Summe (mod 2)
von Produkten der Argumente darstellen:
h =
=  (u
(u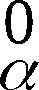 )μ1…(S
)μ1…(S )μ28…(f52)μ287,
wobei
μ = (μ1),μ2, … ,μ287, aμ ∈ {0,1}.
Es ist möglich, eine Folge "angenäherter" kryptologischer
Schaltungen zu erzeugen und zu untersuchen.
Die angenäherte kryptologische Schaltung der Ordnung n = 1,2,…
wird durch die logische Funktionen h
)μ28…(f52)μ287,
wobei
μ = (μ1),μ2, … ,μ287, aμ ∈ {0,1}.
Es ist möglich, eine Folge "angenäherter" kryptologischer
Schaltungen zu erzeugen und zu untersuchen.
Die angenäherte kryptologische Schaltung der Ordnung n = 1,2,…
wird durch die logische Funktionen h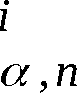 , α = 1,27, i = 1,2,…
beschrieben, die sich aus h
, α = 1,27, i = 1,2,…
beschrieben, die sich aus h bilden lassen, indem man alle
Summanden mit mehr als n Faktoren wegläßt.
Es wurde die Erarbeitung eines Programms für eine EDVA zur
Berechnung solcher Funktionen und ihrer Untersuchung begonnen.
Dabei wird wesentlich ausgenutzt, daß h
bilden lassen, indem man alle
Summanden mit mehr als n Faktoren wegläßt.
Es wurde die Erarbeitung eines Programms für eine EDVA zur
Berechnung solcher Funktionen und ihrer Untersuchung begonnen.
Dabei wird wesentlich ausgenutzt, daß h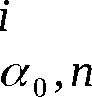 , α= 1,27 berech-
net werden kann, ohne h
, α= 1,27 berech-
net werden kann, ohne h , α= 1,27 zu kennen, bekannt sei
lediglich h
, α= 1,27 zu kennen, bekannt sei
lediglich h , α= 1,27.
§3 Äquivalente Schlüssel
1. Grundlegende Definitionen
Die Frage nach der Existenz und Mächtigkeit von Klassen
äquivalenter Schlüssel ist eine Grundfrage bei der Be-
stimmung der Sicherheit des Chiffrators. Man muß berück-
sichtigen, daß man in der Schlüsselelemente
, α= 1,27.
§3 Äquivalente Schlüssel
1. Grundlegende Definitionen
Die Frage nach der Existenz und Mächtigkeit von Klassen
äquivalenter Schlüssel ist eine Grundfrage bei der Be-
stimmung der Sicherheit des Chiffrators. Man muß berück-
sichtigen, daß man in der Schlüsselelemente  die Beziehungen
der Äquivalenz verschieden definieren kann;zwischen den
verschiedenen Beziehungen existieren in der Regel Ver-
bindungen.
Die wichtigste Beziehung vom kryptologischen Gesichtspunkt
ist die Äquivalenz im folgenden Sinne:
Definition:
Zwei Schlüssel S ∈
die Beziehungen
der Äquivalenz verschieden definieren kann;zwischen den
verschiedenen Beziehungen existieren in der Regel Ver-
bindungen.
Die wichtigste Beziehung vom kryptologischen Gesichtspunkt
ist die Äquivalenz im folgenden Sinne:
Definition:
Zwei Schlüssel S ∈  und S' ∈
und S' ∈  heißen äquivalent bezüg-
lich der Additionsreihe der Länge L, wenn, für festes
U ∈
heißen äquivalent bezüg-
lich der Additionsreihe der Länge L, wenn, für festes
U ∈  , für alle F ∈
, für alle F ∈  gilt
(1.1)
ΨL(U,S,F) = ΨL(U,S',F).
Obwohl es keine unmittelbaren Ergebnisse über äquivalente
Schlüssel bezüglich der Additionsreihe gibt, kann man sagen,
daß alle erhaltenen und unten dargelegten Resultate über
L = 47 die Mächtigkeit der Klasse äquivalenter Schlüssel
bezüglich der Additionsreihe kleiner oder sogar gleich Eins
ist (d.h., äquivalente Schlüssel bezüglich der Additions-
reihe existieren nicht).
Im gesamten Paragraphen setzen wir (P,R) ∈ PR voraus,
obwohl diese Einschränkung nicht mehr notwendig ist.
Wir verwenden die Bezeichnung aus §2, Punkt 1.
2. Äquivalente Schlüssel bezüglich der Folge (Ui)i=1,2,…
Diese Art der Äquivalenz läßt sich leicht Untersuchen. Sie
wird dadurch interessant, daß im Fall der Äquivalenz die
entsprechenden Schlüssel auch äquivalent bezüglich der
Additionsreihe sind.
Wir geben genaue Formulierungen.
Definition:
Zwei Schlüssel S ∈
gilt
(1.1)
ΨL(U,S,F) = ΨL(U,S',F).
Obwohl es keine unmittelbaren Ergebnisse über äquivalente
Schlüssel bezüglich der Additionsreihe gibt, kann man sagen,
daß alle erhaltenen und unten dargelegten Resultate über
L = 47 die Mächtigkeit der Klasse äquivalenter Schlüssel
bezüglich der Additionsreihe kleiner oder sogar gleich Eins
ist (d.h., äquivalente Schlüssel bezüglich der Additions-
reihe existieren nicht).
Im gesamten Paragraphen setzen wir (P,R) ∈ PR voraus,
obwohl diese Einschränkung nicht mehr notwendig ist.
Wir verwenden die Bezeichnung aus §2, Punkt 1.
2. Äquivalente Schlüssel bezüglich der Folge (Ui)i=1,2,…
Diese Art der Äquivalenz läßt sich leicht Untersuchen. Sie
wird dadurch interessant, daß im Fall der Äquivalenz die
entsprechenden Schlüssel auch äquivalent bezüglich der
Additionsreihe sind.
Wir geben genaue Formulierungen.
Definition:
Zwei Schlüssel S ∈  und S' ∈
und S' ∈  heißen äquivalent bezüg-
lich der Folge (Ui)
heißen äquivalent bezüg-
lich der Folge (Ui) beziehungsweise (Ui)i=1,2,…,
wenn für festes U0 ∈
beziehungsweise (Ui)i=1,2,…,
wenn für festes U0 ∈  , für alle F ∈
, für alle F ∈  gilt
(2.1)
Ui(U0,S,F) = Ui(U0,S',F)
für alle i = 1,N, bzw. i= 1,2,…
Im zweiten Fall sei N = + ∞ und wir schreiben (Ui)
gilt
(2.1)
Ui(U0,S,F) = Ui(U0,S',F)
für alle i = 1,N, bzw. i= 1,2,…
Im zweiten Fall sei N = + ∞ und wir schreiben (Ui) .
Theorem:
Für N < 104 sind S und S' genau dann äquivalent, wenn sie
in den ersten N Stellen übereinstimmen.
Für N ≥ 104 existieren keine äquivalenten Schlüssel.
Beweis:
Seien S und S' äquivalent. Dann gilt
Ui(U0,S,F) = ϕ(s
.
Theorem:
Für N < 104 sind S und S' genau dann äquivalent, wenn sie
in den ersten N Stellen übereinstimmen.
Für N ≥ 104 existieren keine äquivalenten Schlüssel.
Beweis:
Seien S und S' äquivalent. Dann gilt
Ui(U0,S,F) = ϕ(s ,s
,s ,ri) Ui-1(U0,S,F) =
Ui(U0,S',F) = ϕ(s
,ri) Ui-1(U0,S,F) =
Ui(U0,S',F) = ϕ(s ',s
',s ',ri) Ui-1(U0,S,F)
Aufgrund der Eigenschaft (§1, 4.3) folgt
(s
',ri) Ui-1(U0,S,F)
Aufgrund der Eigenschaft (§1, 4.3) folgt
(s , s
, s ) = (s
) = (s ', s
', s ') für alle i = 1,N.
Für N < 104 ist das gleichbedeutend mit dem Übereinstimmen
von S und S' in den ersten N Stellen.
Für N ≥ 104 erhalten wir S = S'.
Aus dem Beweis geht hervor, daß das Theorem gültig bleibt,
wenn in der Definition der Äquivalenz die Gleichung (2.1)
nicht für alle, sondern nur für ein F ∈
') für alle i = 1,N.
Für N < 104 ist das gleichbedeutend mit dem Übereinstimmen
von S und S' in den ersten N Stellen.
Für N ≥ 104 erhalten wir S = S'.
Aus dem Beweis geht hervor, daß das Theorem gültig bleibt,
wenn in der Definition der Äquivalenz die Gleichung (2.1)
nicht für alle, sondern nur für ein F ∈  gilt.
Eine bedeutend kompliziertere Situation tritt in dem Fall
ein, wenn Teilfolgen, z. B. (U104i)
gilt.
Eine bedeutend kompliziertere Situation tritt in dem Fall
ein, wenn Teilfolgen, z. B. (U104i) , der Folge (Ui)
, der Folge (Ui) betrachtet werden.
Nur für den Fall (Uni)
betrachtet werden.
Nur für den Fall (Uni) für n = 2 und n = 3 kann man
analoge Theoreme zeigen, indem man (§1, 4.8) und (§1, 4.11)
anwendet.
3. Äquivalente Schlüssel bezüglich UN
3.1. Definition
Zwei Schlüssel S ∈
für n = 2 und n = 3 kann man
analoge Theoreme zeigen, indem man (§1, 4.8) und (§1, 4.11)
anwendet.
3. Äquivalente Schlüssel bezüglich UN
3.1. Definition
Zwei Schlüssel S ∈  und S' ∈
und S' ∈  heißen äquivalent be-
züglich UN, N - natürliche Zahl, falls die Gleichung
(3.1)
UN(U0),S,F) = UN(U0),S',F)
für alle F ∈
heißen äquivalent be-
züglich UN, N - natürliche Zahl, falls die Gleichung
(3.1)
UN(U0),S,F) = UN(U0),S',F)
für alle F ∈  und für alle U0 ∈
und für alle U0 ∈  gilt.
In diesem Falle werden wir die Bezeichnungen S
gilt.
In diesem Falle werden wir die Bezeichnungen S 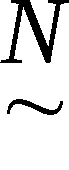 S' benutzen.
Bei N < 104 sind offensichtlich alle Schlüssel, die sich von-
einander nur in den Stellen N+1, N+2, … , 104 unterscheiden,
äquivalent bezüglich UN.
Wir definieren die Abbildung ρ = ρ(r) der Menge
S' benutzen.
Bei N < 104 sind offensichtlich alle Schlüssel, die sich von-
einander nur in den Stellen N+1, N+2, … , 104 unterscheiden,
äquivalent bezüglich UN.
Wir definieren die Abbildung ρ = ρ(r) der Menge  auf
auf
 durch die Formel
(3.2)
(r ∈{0,1})
ρ(r)U=(u1,u2,u3,u4+r,u5,u27).
Dann kann man schreiben
(3.3)
ϕ(s1,s2,r)U = ρ(r)ϕ(s1,s2,0)U.
Sei
durch die Formel
(3.2)
(r ∈{0,1})
ρ(r)U=(u1,u2,u3,u4+r,u5,u27).
Dann kann man schreiben
(3.3)
ϕ(s1,s2,r)U = ρ(r)ϕ(s1,s2,0)U.
Sei 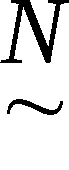 S', S ≠ S'.
Wir bezeichnen
s' = ( (s
S', S ≠ S'.
Wir bezeichnen
s' = ( (s ',s
',s '), …, (s
'), …, (s ',s
',s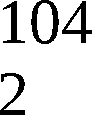 ') ),
ϕi = ϕ(s
') ),
ϕi = ϕ(s , s
, s , 0) ϕi' = ϕ(s
, 0) ϕi' = ϕ(s ', s
', s ', 0), ρi = ρ(ri)
v = min {i:ϕi≠ϕi'}, μ = max{i:ϕi≠ϕi'}.
Bei N ≥ 104 gilt offensichtlich v ≤ 104. Bei N < 104
nehmen wir an, daß v und μ existieren (d.h., S und S'
fallen an den N ersten Stellen nicht zusammen).
S
', 0), ρi = ρ(ri)
v = min {i:ϕi≠ϕi'}, μ = max{i:ϕi≠ϕi'}.
Bei N ≥ 104 gilt offensichtlich v ≤ 104. Bei N < 104
nehmen wir an, daß v und μ existieren (d.h., S und S'
fallen an den N ersten Stellen nicht zusammen).
S 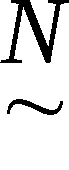 S' kann man in der Form schreiben:
ρN ϕNρN-1 … ϕ1U0 = ρN ϕ'N ρN-1 … ϕ
S' kann man in der Form schreiben:
ρN ϕNρN-1 … ϕ1U0 = ρN ϕ'N ρN-1 … ϕ U0
für alle F ∈
U0
für alle F ∈  und alle U0 ∈
und alle U0 ∈  ,
oder
(3.4)
ϕNρN-1 … ϕ1 = ϕ'NρN-1 … ϕ
,
oder
(3.4)
ϕNρN-1 … ϕ1 = ϕ'NρN-1 … ϕ für alle F ∈
für alle F ∈  .
Aus μ = v folgt auch unmittelbar ϕμ ≠ ϕ'μ,
deshalb gilt:
Falls S
.
Aus μ = v folgt auch unmittelbar ϕμ ≠ ϕ'μ,
deshalb gilt:
Falls S 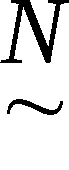 S', dann unterscheiden sich S und S' mindestens
an zwei Stellen.
Weiter gilt:
Falls S
S', dann unterscheiden sich S und S' mindestens
an zwei Stellen.
Weiter gilt:
Falls S 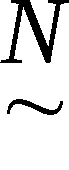 S' so ist μ z v+3.
Wir beweisen diese Behauptung für μ = v+2 (der Fall
μ=v+1 ist analog): Aus (3.4) würde folgen
ϕv+2 ρv+1 ϕv+1 ρv ϕv = ϕ'v+2 ρv+1 ϕ'v+1 ρv ϕ'v1
daraus folgt für alle ρv, ρv+1, d.h.
ϕv+2ϕv+1ϕv = ϕ'v+2ϕ'v+1ϕ'v,
was nicht sein kann.
Daraus folgt, daß S
S' so ist μ z v+3.
Wir beweisen diese Behauptung für μ = v+2 (der Fall
μ=v+1 ist analog): Aus (3.4) würde folgen
ϕv+2 ρv+1 ϕv+1 ρv ϕv = ϕ'v+2 ρv+1 ϕ'v+1 ρv ϕ'v1
daraus folgt für alle ρv, ρv+1, d.h.
ϕv+2ϕv+1ϕv = ϕ'v+2ϕ'v+1ϕ'v,
was nicht sein kann.
Daraus folgt, daß S 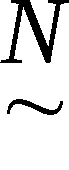 S' nicht gelten kann, falls
S und S' nicht identisch an den ersten N Stellen sind,
für N = 1,2,3.
Zur Betrachtung des allgemeinen Falles führen wir die
Abbildungen
ω = ω(μ,v;F) = ϕμ-1 ρμ-2 ϕμ-2 … ϕv
ω' = ω'(μ,v;F) = ϕ'μ-1 ρμ-2 ϕ'μ-2 … ϕv.
ein.
Aus (3.4) folgt für alle F ∈
S' nicht gelten kann, falls
S und S' nicht identisch an den ersten N Stellen sind,
für N = 1,2,3.
Zur Betrachtung des allgemeinen Falles führen wir die
Abbildungen
ω = ω(μ,v;F) = ϕμ-1 ρμ-2 ϕμ-2 … ϕv
ω' = ω'(μ,v;F) = ϕ'μ-1 ρμ-2 ϕ'μ-2 … ϕv.
ein.
Aus (3.4) folgt für alle F ∈  ϕμρμ-1ω = ϕ'μρμ-1ω'.
Dabei ist zu berücksichtigen, daß bei a ≥ 52 die Parame-
ter ri+1, ri+2, … ,ri+a nicht als unabhängig voneinan-
der angenommen werden dürfen. Deshalb setzen wir zusätzlich
μ ≤ v+51 voraus.
Für rμ-1 = 0 erhalten wir
ω' = (ϕ'μ)-1ϕμω,
und für rμ-1 = 1
ϕμρ(1)ω = ϕ'μρ(1)(ϕ'μ)-1ϕμω.
Deshalb gilt
ϕμρ(1) = ϕ'μρ(1)(ϕ'μ)-1ϕμ
oder
ϕμρ(1)ϕμ-1 = ϕ'μρ(1)(ϕ'μ)-1
Daraus folgt eine notwendige Bedingung für die Existenz
äquivalenter Schlüssel bezüglich UN:
Falls bei gegebenen (P,R) ∈ PR für ein natürliches N S ∈
ϕμρμ-1ω = ϕ'μρμ-1ω'.
Dabei ist zu berücksichtigen, daß bei a ≥ 52 die Parame-
ter ri+1, ri+2, … ,ri+a nicht als unabhängig voneinan-
der angenommen werden dürfen. Deshalb setzen wir zusätzlich
μ ≤ v+51 voraus.
Für rμ-1 = 0 erhalten wir
ω' = (ϕ'μ)-1ϕμω,
und für rμ-1 = 1
ϕμρ(1)ω = ϕ'μρ(1)(ϕ'μ)-1ϕμω.
Deshalb gilt
ϕμρ(1) = ϕ'μρ(1)(ϕ'μ)-1ϕμ
oder
ϕμρ(1)ϕμ-1 = ϕ'μρ(1)(ϕ'μ)-1
Daraus folgt eine notwendige Bedingung für die Existenz
äquivalenter Schlüssel bezüglich UN:
Falls bei gegebenen (P,R) ∈ PR für ein natürliches N S ∈  und
S' ∈
und
S' ∈  , S ≠ S', μ ≤ v+51 mit der Eigenschaft S
, S ≠ S', μ ≤ v+51 mit der Eigenschaft S 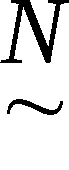 S'
existieren (für N < 104 wird zusätzlich vorausgesetzt, daß
S und S' an den ersten N Stellen nicht identisch sind) dann
gibt es Paare
(s1,s2) ∈ {0,1}2 und (s
S'
existieren (für N < 104 wird zusätzlich vorausgesetzt, daß
S und S' an den ersten N Stellen nicht identisch sind) dann
gibt es Paare
(s1,s2) ∈ {0,1}2 und (s ,s
,s ) ∈ {0,1}2, (s1,s2) ≠ (s
) ∈ {0,1}2, (s1,s2) ≠ (s ,s
,s )
mit der Eigenschaft
(3.5)
ϕ(s1,s2,0) ρ(1) ϕ-1(s1,s2,0) =
ϕ(s
)
mit der Eigenschaft
(3.5)
ϕ(s1,s2,0) ρ(1) ϕ-1(s1,s2,0) =
ϕ(s ,s
,s ,0) ρ(1) ϕ-1(s
,0) ρ(1) ϕ-1(s ,s
,s ,0).
In anderer Formulierung erhält man eine hinreichende Bedin-
gung der Nichtexistenz äquivalenter Schlüssel bezüglich UN:
Falls bei gegebenen (P,R) ∈ PR für beliebige Paare
(s1,s2) ∈ {0,1}2 und (s
,0).
In anderer Formulierung erhält man eine hinreichende Bedin-
gung der Nichtexistenz äquivalenter Schlüssel bezüglich UN:
Falls bei gegebenen (P,R) ∈ PR für beliebige Paare
(s1,s2) ∈ {0,1}2 und (s ,s
,s ) ∈ {0,1}2 aus der Gültigkeit
von (3.5) folgt (s1,s2) = (s
) ∈ {0,1}2 aus der Gültigkeit
von (3.5) folgt (s1,s2) = (s ,s
,s ) dann existieren für kein natürliches
N < 104 S und S' mit der Eigenschaft S
) dann existieren für kein natürliches
N < 104 S und S' mit der Eigenschaft S 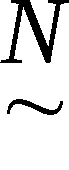 S', die an den ersten
N Stellen nicht identisch sind und μ ≤ v+51 genügen, aber
auch für natürliches N ≥ 104 existieren keine S ∈
S', die an den ersten
N Stellen nicht identisch sind und μ ≤ v+51 genügen, aber
auch für natürliches N ≥ 104 existieren keine S ∈  und S' ∈
und S' ∈  .
S ≠ S', die auch μ ≤ v+51 genügen, mit der Eigenschaft
S
.
S ≠ S', die auch μ ≤ v+51 genügen, mit der Eigenschaft
S 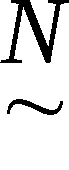 S'.
Aus dem Gang der Darlegung folgt die Notwendigkeit der
Gültigkeit von (3.1) für alle U0 ∈
S'.
Aus dem Gang der Darlegung folgt die Notwendigkeit der
Gültigkeit von (3.1) für alle U0 ∈  .
Es gelang nicht, irgendwelche ähnlichen Ergebnisse für den
der Realität näheren Fall der Äquivalenz bezüglich UN zu
erhalten, falls die Gleichung (3.1) nur für ein festes
U0 ∈
.
Es gelang nicht, irgendwelche ähnlichen Ergebnisse für den
der Realität näheren Fall der Äquivalenz bezüglich UN zu
erhalten, falls die Gleichung (3.1) nur für ein festes
U0 ∈  erfüllt ist.
Eine wesentliche Einschränkung stellt auch die Bedingung
μ ≤ v+51 dar.
Von ihr kann man sich nur lösen, wenn man die Äquivalenz
in der Weise definiert, daß alle Folgen
{r1,r2, …, rN} ∈ {0,1}N
zugelassen sind.
Wegen (3.4) folgt aus S
erfüllt ist.
Eine wesentliche Einschränkung stellt auch die Bedingung
μ ≤ v+51 dar.
Von ihr kann man sich nur lösen, wenn man die Äquivalenz
in der Weise definiert, daß alle Folgen
{r1,r2, …, rN} ∈ {0,1}N
zugelassen sind.
Wegen (3.4) folgt aus S 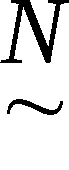 S' für alle k = 1,2,3,…
S
S' für alle k = 1,2,3,…
S  S'.
Wünschenswert wäre es, eine notwendige und hinreichende
Bedingung für die Existenz äquivalenter Schlüssel bezüglich
UN zu erreichen, aber der vorliegende Gedankengang
ist nicht umkehrbar.
3.2. Wir betrachten die Gleichung (3.5) und ersetzen sie durch
einfachere äquivalente Bedingungen.
Wir bezeichnen:
U = (ui)
S'.
Wünschenswert wäre es, eine notwendige und hinreichende
Bedingung für die Existenz äquivalenter Schlüssel bezüglich
UN zu erreichen, aber der vorliegende Gedankengang
ist nicht umkehrbar.
3.2. Wir betrachten die Gleichung (3.5) und ersetzen sie durch
einfachere äquivalente Bedingungen.
Wir bezeichnen:
U = (ui) , V = (vi)
, V = (vi) , W = (wi)
, W = (wi) , Y = (yi)
, Y = (yi) ,
ϕ-1(s1,s2,0)U=V, ρ(1)V = W, ϕ(s1, s2, 0)W = Y,
Z1 = Z(s2,vP1, …, vP5) + Z(s2,wP1, …, wP5),
Z2 = Z(vP7, …, vP12) + Z(wP7, …, wP12),
Z3 = Z(vP14, …, vP19) + Z(wP14, …, wP19),
Z4 = Z(vP21, …, vP26) + Z(wP21, …, wP26).
Dann gilt nach Definition für ɳ=1,9
u3ɳ-2 = v3ɳ-3 + ∆ɳ + Tɳ(s2,vP)
u3ɳ-1 = v3ɳ-2, u3ɳ) = v3ɳ-1, v0=s1;
w3ɳ-2 = v3ɳ-2 + 1, w3ɳ-1 = v3ɳ-1, w3ɳ = v3ɳ;
y3ɳ-2 = w3ɳ-3 + ∆ɳs2 + Tɳ(s2,wP)
y3ɳ-1 = w3ɳ-2, y3ɳ = w3ɳ-1, w0 = s1.
Man muß Bedingungen finden, unter denen das Element Y ∈
,
ϕ-1(s1,s2,0)U=V, ρ(1)V = W, ϕ(s1, s2, 0)W = Y,
Z1 = Z(s2,vP1, …, vP5) + Z(s2,wP1, …, wP5),
Z2 = Z(vP7, …, vP12) + Z(wP7, …, wP12),
Z3 = Z(vP14, …, vP19) + Z(wP14, …, wP19),
Z4 = Z(vP21, …, vP26) + Z(wP21, …, wP26).
Dann gilt nach Definition für ɳ=1,9
u3ɳ-2 = v3ɳ-3 + ∆ɳ + Tɳ(s2,vP)
u3ɳ-1 = v3ɳ-2, u3ɳ) = v3ɳ-1, v0=s1;
w3ɳ-2 = v3ɳ-2 + 1, w3ɳ-1 = v3ɳ-1, w3ɳ = v3ɳ;
y3ɳ-2 = w3ɳ-3 + ∆ɳs2 + Tɳ(s2,wP)
y3ɳ-1 = w3ɳ-2, y3ɳ = w3ɳ-1, w0 = s1.
Man muß Bedingungen finden, unter denen das Element Y ∈  für mindestens ein U ∈
für mindestens ein U ∈  4 verschiedene Werte annimmt, wenn
das Paar (s1,s2) 4 verschiedene Werte annimmt.
Wir vergleichen die verschiedenen, oben angegebenen
Bedingungen und erhalten
y3ɳ-2 = u3ɳ-2 Tɳ(s2,vP) + Tɳ(s2,wP),
y3ɳ-1 = u3ɳ-1 + 1, y3ɳ = u3ɳ,
hieraus folgt, daß nur die 8 Werte y3ɳ-1, ɳ=1,9, ɳ ≠ R1
von s1 und s2 abhängen können.
Wir haben
y3R-2 = u3R-2 + Z1
y3R-2 = u3R-2 + Z1 + vP6 + wP6
y3R-2 = u3R-2 + Z1 + vP6 + wP6 + Z2
…
y3R-2 = u3R-2 + Z1 + … Z4 + vP27 + wP27
Die Summe vα + wα hängt nicht von s1 und s2 ab. Deshalb
nimmt Y genau dann 4 verschiedene Werte an, wenn das
Tupel Z = (Z1, Z2, Z3, Z4) 4 verschiedene Werte annimmt (weil
das dazu äquivalent ist, daß das Tupel (Z1,Z1+Z2, Z1+Z2+Z3,
Z1+Z2+Z3+Z4) 4 verschiedene Werte annimmt.)
Folglich kann man dieses Resultat formulieren:
Aus der Gleichung (3.5) folgt genau dann (s1,s2) = (s
4 verschiedene Werte annimmt, wenn
das Paar (s1,s2) 4 verschiedene Werte annimmt.
Wir vergleichen die verschiedenen, oben angegebenen
Bedingungen und erhalten
y3ɳ-2 = u3ɳ-2 Tɳ(s2,vP) + Tɳ(s2,wP),
y3ɳ-1 = u3ɳ-1 + 1, y3ɳ = u3ɳ,
hieraus folgt, daß nur die 8 Werte y3ɳ-1, ɳ=1,9, ɳ ≠ R1
von s1 und s2 abhängen können.
Wir haben
y3R-2 = u3R-2 + Z1
y3R-2 = u3R-2 + Z1 + vP6 + wP6
y3R-2 = u3R-2 + Z1 + vP6 + wP6 + Z2
…
y3R-2 = u3R-2 + Z1 + … Z4 + vP27 + wP27
Die Summe vα + wα hängt nicht von s1 und s2 ab. Deshalb
nimmt Y genau dann 4 verschiedene Werte an, wenn das
Tupel Z = (Z1, Z2, Z3, Z4) 4 verschiedene Werte annimmt (weil
das dazu äquivalent ist, daß das Tupel (Z1,Z1+Z2, Z1+Z2+Z3,
Z1+Z2+Z3+Z4) 4 verschiedene Werte annimmt.)
Folglich kann man dieses Resultat formulieren:
Aus der Gleichung (3.5) folgt genau dann (s1,s2) = (s ,s
,s ),
wenn für mindestens ein U ∈
),
wenn für mindestens ein U ∈  Z vier verschiedene Werte
annimmt, wenn (s1,s2) alle möglichen Werte durchläuft.
Diese Frage wird nur gelöst, indem man konkrete (P,R)
betrachtet.
4. Äquivalente Schlüssel bezüglich der Folge (u
Z vier verschiedene Werte
annimmt, wenn (s1,s2) alle möglichen Werte durchläuft.
Diese Frage wird nur gelöst, indem man konkrete (P,R)
betrachtet.
4. Äquivalente Schlüssel bezüglich der Folge (u )i=1,2,…
4.1. Definition
Zwei Schlüssel S ∈
)i=1,2,…
4.1. Definition
Zwei Schlüssel S ∈  und S' ∈
und S' ∈  heißen äquivalent bezüglich der
Folge (u
heißen äquivalent bezüglich der
Folge (u )
) , wobei α eine feste Zahl aus dem Bereich
1,27 ist, Wenn für alle U ∈
, wobei α eine feste Zahl aus dem Bereich
1,27 ist, Wenn für alle U ∈  und für alle F ∈
und für alle F ∈  gilt:
(4.1)
u
gilt:
(4.1)
u (U,S,F) = u
(U,S,F) = u (U,S',F)
für alle i = 1,N.
Wir lassen N = ∞ zu.
u
(U,S',F)
für alle i = 1,N.
Wir lassen N = ∞ zu.
u (U,S,F) - das ist die Komponente mit der Nummer α
des Elements Ui = Ui(U,S,F) = u
(U,S,F) - das ist die Komponente mit der Nummer α
des Elements Ui = Ui(U,S,F) = u
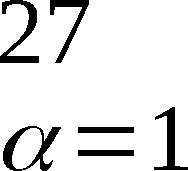 ∈
∈  Theorem:
Für N < 104 sind S und S' genau dann äquivalent bezüglich
(u
Theorem:
Für N < 104 sind S und S' genau dann äquivalent bezüglich
(u )
) , wenn sie in den ersten N Stellen übereinstimmen.
Für N ≥ existieren keine äquivalenten Schlüssel
bezüglich (u
, wenn sie in den ersten N Stellen übereinstimmen.
Für N ≥ existieren keine äquivalenten Schlüssel
bezüglich (u )
) .
Beweis:
(1) Seien S und S' äquivalent. Wir zeigen, daß dann S = S'
gilt (zumindestens auf den ersten N Stellen für N < 104).
Wir haben
u
.
Beweis:
(1) Seien S und S' äquivalent. Wir zeigen, daß dann S = S'
gilt (zumindestens auf den ersten N Stellen für N < 104).
Wir haben
u = s
= s + r1 + s
+ r1 + s ∆1 + T1(s
∆1 + T1(s ,uP) =
s
,uP) =
s ' + r1 + s
' + r1 + s '∆1 + T1(s
'∆1 + T1(s ',uP).
Sei Z(e1+e2, …,e6) = e1Z1(e2, … , e6) + Z2(e2, … , e6).
Dann folgt aus den Darstellungen für u
',uP).
Sei Z(e1+e2, …,e6) = e1Z1(e2, … , e6) + Z2(e2, … , e6).
Dann folgt aus den Darstellungen für u s
s +s
+s '+(s
'+(s +s
+s ')∆1 = (s
')∆1 = (s +s
+s ')Z1(uP1, …, uP5).
Für s
')Z1(uP1, …, uP5).
Für s ≠s
≠s ' folgt s
' folgt s = s
= s '.
Für s
'.
Für s ≠s
≠s ' nimmt die rechte Seite in Abhängigkeit von U
die Werte 0 und 1 an. Aber das widerspricht dem, daß
die linke Seite nicht von U abhängt.
(2) Das Theorem sei für N-1 bewiesen; wir betrachten N.
Seien S und S' äquivalent für N. Dann stimmen sie aufgrund
der Induktionsvoraussetzung und der Definition (4.1)
in den ersten N-1 Stellen überein.
Deshalb ist
UN-1(U,S,F) = UN-1(U,S',F) und u
' nimmt die rechte Seite in Abhängigkeit von U
die Werte 0 und 1 an. Aber das widerspricht dem, daß
die linke Seite nicht von U abhängt.
(2) Das Theorem sei für N-1 bewiesen; wir betrachten N.
Seien S und S' äquivalent für N. Dann stimmen sie aufgrund
der Induktionsvoraussetzung und der Definition (4.1)
in den ersten N-1 Stellen überein.
Deshalb ist
UN-1(U,S,F) = UN-1(U,S',F) und u hat folgende Darstellung
u
hat folgende Darstellung
u = s
= s + rN + s
+ rN + s ∆1 + T1(s
∆1 + T1(s , u
, u ) =
= s
) =
= s ' + rN + s
' + rN + s '∆1 + T1(s
'∆1 + T1(s ', u
', u ).
Die weiteren Überlegungen erfolgen analog zu (2).
Eine Betrachtung des Beweises zeigt, daß das Theorem
gültig bleibt, wenn (4.1) nur für ein F ∈
).
Die weiteren Überlegungen erfolgen analog zu (2).
Eine Betrachtung des Beweises zeigt, daß das Theorem
gültig bleibt, wenn (4.1) nur für ein F ∈  gilt.
Aber wesentlich ist die Einschränkung auf den Fall α = 1.
§4 Stochastische Modelle der Chiffrierabbildung
1. Markowsche Kette
Wir definieren folgende Markowsche Kette:
gilt.
Aber wesentlich ist die Einschränkung auf den Fall α = 1.
§4 Stochastische Modelle der Chiffrierabbildung
1. Markowsche Kette
Wir definieren folgende Markowsche Kette:
 sei die Menge der Zustände der Kette; der Anfangszustand
sei ein beliebiges U ∈
sei die Menge der Zustände der Kette; der Anfangszustand
sei ein beliebiges U ∈  , wobei alle Anfangszustände
gleichwahrscheinlich sind; der Übergang von einem zustand
in einen anderen wird durch die Abbildung ϕ verwirklicht,
d.h., durch die Formeln (§1, 1.1);
(P,R) seinen fest (wir betrachteten (P,R) ∈ PR); (u0,s,r) sei
ein zufälliger Vektor, der alle 8 Werte gleichwahrscheinlich
annimmt.
Dieses Modell unterscheidet sich von der kryptologischen Schal-
tung dadurch, daß in ihr der Anfangszustand fest (Langzeit-
schlüssel) und die Vektorfolge (u
, wobei alle Anfangszustände
gleichwahrscheinlich sind; der Übergang von einem zustand
in einen anderen wird durch die Abbildung ϕ verwirklicht,
d.h., durch die Formeln (§1, 1.1);
(P,R) seinen fest (wir betrachteten (P,R) ∈ PR); (u0,s,r) sei
ein zufälliger Vektor, der alle 8 Werte gleichwahrscheinlich
annimmt.
Dieses Modell unterscheidet sich von der kryptologischen Schal-
tung dadurch, daß in ihr der Anfangszustand fest (Langzeit-
schlüssel) und die Vektorfolge (u ,si,ri)i determiniert ist,
wobei man nur gewisse Anfangswerte als beliebig ansehen kann.
Betrachten wir zu Beginn die Übergangsmatrix Π. Die Abbil-
dung ϕ = ϕ(u0,s,r) realisiert eine Permutation der
Menge
,si,ri)i determiniert ist,
wobei man nur gewisse Anfangswerte als beliebig ansehen kann.
Betrachten wir zu Beginn die Übergangsmatrix Π. Die Abbil-
dung ϕ = ϕ(u0,s,r) realisiert eine Permutation der
Menge  . Diese Permutation entspricht auf allbekannte
Weise eine quadratische Matrix Π(u0,s,r) der Ordnung 227 aus
Nullen und Einsen, welche in jeder Zeile und jeder Spalte
genau eine Eins hat.
Dann hat Π das Aussehen:
Π = 1/8 ∑ Π(u0,s,r),
die Summe wird über sämtliche Werte des Vektors
(u0,s,r) ∈ {0,1}3
genommen.
In beliebiger Zeile und in beliebiger Spalte der Matrix Π
befindet sich an genau 8 Stellen der Wert 1/8, und an allen
übrigen Stellen steht Null. Das folgt aus (§1, 4.3) und
(§1, 4.15). Daher ist die Matrix Π doppelt stochastisch.
(Das heißt, die Summe aller Zeilen und aller Spalten sind
gleich Eins.)
Ein Zustand U ∈
. Diese Permutation entspricht auf allbekannte
Weise eine quadratische Matrix Π(u0,s,r) der Ordnung 227 aus
Nullen und Einsen, welche in jeder Zeile und jeder Spalte
genau eine Eins hat.
Dann hat Π das Aussehen:
Π = 1/8 ∑ Π(u0,s,r),
die Summe wird über sämtliche Werte des Vektors
(u0,s,r) ∈ {0,1}3
genommen.
In beliebiger Zeile und in beliebiger Spalte der Matrix Π
befindet sich an genau 8 Stellen der Wert 1/8, und an allen
übrigen Stellen steht Null. Das folgt aus (§1, 4.3) und
(§1, 4.15). Daher ist die Matrix Π doppelt stochastisch.
(Das heißt, die Summe aller Zeilen und aller Spalten sind
gleich Eins.)
Ein Zustand U ∈  heißt wesentlich, wenn für alle V ∈
heißt wesentlich, wenn für alle V ∈  gilt:
falls man von U, nach mehrmaliger Anwendung der Abbildung ϕ,
möglicherweise mit verschiedenen Parametern, zu V gelangen
kann, so kann man auch von V durch wiederholte Anwendung der
Abbildung ϕ zu U gelangen.
Wegen der Eineindeutigkeit von ϕ sind alle Zustände
wesentlich.
Die Menge
gilt:
falls man von U, nach mehrmaliger Anwendung der Abbildung ϕ,
möglicherweise mit verschiedenen Parametern, zu V gelangen
kann, so kann man auch von V durch wiederholte Anwendung der
Abbildung ϕ zu U gelangen.
Wegen der Eineindeutigkeit von ϕ sind alle Zustände
wesentlich.
Die Menge  kann man vollständig in Klassen wesentlicher
Zustände zerlegen, wobei in jeder Klasse alle die Zustände
vereint sind, die ineinander übergehen können. Diese Klassen
stimmen mit den Zustandsklassen überein, die in §1 Punkt 4.1
definiert sind.
Satz:
Falls eine Klasse wesentlicher Zustände einen Fixpunkt
enthält, dann sind alle Zustände dieser Klasse asymptomatisch
gleichverteilt.
Beweis:
Aus der Theorie der Markowschen Ketten ist bekannt, daß die
Zustände aus einer Klasse wesentlicher Zustände asymptomatisch
gleichverteilt sind, dann kann man bei hinreichend großem K
aus einen Zustand in einen anderen in K und in K+1 Schritten
gelangen, indem man über den Fixpunkt geht. Aber das ist
gleichbedeutend mit der Aperiodizität der Klasse.
Bemerkung:
Die Voraussetzung über die Existenz eines Fixpunktes kann man
durch eine beliebige andere hinreichende Bedingung der Aperio-
dizität der Zustandsklassen ersetzen.
Wir setzen voraus, daß alle Zustande eine Klasse bilden
(welche mit der Menge
kann man vollständig in Klassen wesentlicher
Zustände zerlegen, wobei in jeder Klasse alle die Zustände
vereint sind, die ineinander übergehen können. Diese Klassen
stimmen mit den Zustandsklassen überein, die in §1 Punkt 4.1
definiert sind.
Satz:
Falls eine Klasse wesentlicher Zustände einen Fixpunkt
enthält, dann sind alle Zustände dieser Klasse asymptomatisch
gleichverteilt.
Beweis:
Aus der Theorie der Markowschen Ketten ist bekannt, daß die
Zustände aus einer Klasse wesentlicher Zustände asymptomatisch
gleichverteilt sind, dann kann man bei hinreichend großem K
aus einen Zustand in einen anderen in K und in K+1 Schritten
gelangen, indem man über den Fixpunkt geht. Aber das ist
gleichbedeutend mit der Aperiodizität der Klasse.
Bemerkung:
Die Voraussetzung über die Existenz eines Fixpunktes kann man
durch eine beliebige andere hinreichende Bedingung der Aperio-
dizität der Zustandsklassen ersetzen.
Wir setzen voraus, daß alle Zustande eine Klasse bilden
(welche mit der Menge  zusammenfällt) und daß es einen
Fixpunkt gibt.
Analog zu §2, Punkt 1 definieren wir die unendliche Folge
A = Ψ(U,S,F). Im gegebenen Modell entspricht a der Additions-
reihe, die in §2 definiert ist, wenn sie bis ins Unendliche
fortgesetzt wird.
Falls U die gesamte Klasse durchläuft, d.h., die gesamte
Menge
zusammenfällt) und daß es einen
Fixpunkt gibt.
Analog zu §2, Punkt 1 definieren wir die unendliche Folge
A = Ψ(U,S,F). Im gegebenen Modell entspricht a der Additions-
reihe, die in §2 definiert ist, wenn sie bis ins Unendliche
fortgesetzt wird.
Falls U die gesamte Klasse durchläuft, d.h., die gesamte
Menge  , dann nimmt die Komponente uα, α ∈1,27, die
Werte 0 und 1 zur Hälfte an. Deshalb kommen die Werte 0 und
1, nach dem bewiesenen Satz, in A asymptomatisch gleichwahr-
scheinlich vor.
Mit anderen Worten, bei hinreichend großem i nimmt in
A =(ai)i=1,2,… das Element ai die Werte 0 und 1 praktisch
gleichhäufig an.
Sei die Anzahl der Klassen größer als Eins. Dann erhält man
ein ebenso günstiges Resultat, wenn die Klasse, die U = U0
enthält, aperiodisch ist und wenn in ihr die Komponente
uα 0 und 1 zur Hälfte annimmt.
2. Ein anderes Modell
2.1. Wir ändern das Modell, das im §2, Punkt 1 beschrieben ist,
in der Weise ab, daß die Folge (ri)i=1,2,… eine zufällige
gleichwahrscheinliche Folge ist, d.h., eine Folgeunabhän-
giger Realisierungen einer Zufallsgröße, die die Werte 0
und 1 mit gleicher Wahrscheinlichkeit annimmt. Alles übrige
im Modell lassen wir unverändert.
Satz:
Im beschriebenen Modell mit festem U0 ∈
, dann nimmt die Komponente uα, α ∈1,27, die
Werte 0 und 1 zur Hälfte an. Deshalb kommen die Werte 0 und
1, nach dem bewiesenen Satz, in A asymptomatisch gleichwahr-
scheinlich vor.
Mit anderen Worten, bei hinreichend großem i nimmt in
A =(ai)i=1,2,… das Element ai die Werte 0 und 1 praktisch
gleichhäufig an.
Sei die Anzahl der Klassen größer als Eins. Dann erhält man
ein ebenso günstiges Resultat, wenn die Klasse, die U = U0
enthält, aperiodisch ist und wenn in ihr die Komponente
uα 0 und 1 zur Hälfte annimmt.
2. Ein anderes Modell
2.1. Wir ändern das Modell, das im §2, Punkt 1 beschrieben ist,
in der Weise ab, daß die Folge (ri)i=1,2,… eine zufällige
gleichwahrscheinliche Folge ist, d.h., eine Folgeunabhän-
giger Realisierungen einer Zufallsgröße, die die Werte 0
und 1 mit gleicher Wahrscheinlichkeit annimmt. Alles übrige
im Modell lassen wir unverändert.
Satz:
Im beschriebenen Modell mit festem U0 ∈  und S ∈
und S ∈  ist die Additionsreihe AL eine zufällige gleichwahrschein-
liche Folge.
Beweis:
(1) Betrachten wir u
ist die Additionsreihe AL eine zufällige gleichwahrschein-
liche Folge.
Beweis:
(1) Betrachten wir u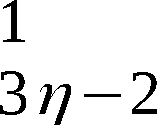 für irgend ein ɳ ∈ 1,9 und i=1,2,…:
u
für irgend ein ɳ ∈ 1,9 und i=1,2,…:
u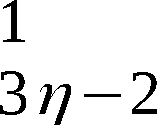 = u
= u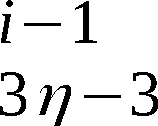 +ri+si∆ɳ+Tɳ(si,u
+ri+si∆ɳ+Tɳ(si,u ).
Daraus wird unmittelbar klar, daß u
).
Daraus wird unmittelbar klar, daß u Werte unabhän-
gig von Ui-1, Ui-2, … annimmt, da ri nicht auf diese
Größen wirkt, und gleichwahrscheinlich ist, da ri
gleichwahrscheinliche Werte annimmt.
(2) Der Fall α ≠ 3ɳ-2 ist analog wegen
u
Werte unabhän-
gig von Ui-1, Ui-2, … annimmt, da ri nicht auf diese
Größen wirkt, und gleichwahrscheinlich ist, da ri
gleichwahrscheinliche Werte annimmt.
(2) Der Fall α ≠ 3ɳ-2 ist analog wegen
u = u
= u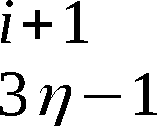 = u
= u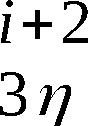 .
(3) Die Teilfolge (gn i)i=1,2…, n - natürlich, der
zufälligen gleichwahrscheinlichen Folge (gi)i=1,2…
ist ebenfalls zufällig und gleichwahrscheinlich.
Bemerkung:
Es wurde bewiesen: Für festes α ∈ 1,27 ist die Folge
(u
.
(3) Die Teilfolge (gn i)i=1,2…, n - natürlich, der
zufälligen gleichwahrscheinlichen Folge (gi)i=1,2…
ist ebenfalls zufällig und gleichwahrscheinlich.
Bemerkung:
Es wurde bewiesen: Für festes α ∈ 1,27 ist die Folge
(u )i=1,2,… zufällig und gleichwahrscheinlich (für α=3ɳ-1
mit Ausnahme von u
)i=1,2,… zufällig und gleichwahrscheinlich (für α=3ɳ-1
mit Ausnahme von u , für α=3ɳ mit Ausnahme von u
, für α=3ɳ mit Ausnahme von u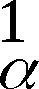 und u
und u ).
2.2 Dieses Modell unterscheidet sich von der kryptologischen
Schaltung weniger, als die in Punkt 1 untersuchte Markowsche
Kette, aber es wurde ein stärkeres Ergebnis erhalten. Der
Unterschied zur kryptologischen Schaltung besteht nur darin,
daß in ihr (ri)i=1,2,… eine determinierte Folge ist.
In ai = u
).
2.2 Dieses Modell unterscheidet sich von der kryptologischen
Schaltung weniger, als die in Punkt 1 untersuchte Markowsche
Kette, aber es wurde ein stärkeres Ergebnis erhalten. Der
Unterschied zur kryptologischen Schaltung besteht nur darin,
daß in ihr (ri)i=1,2,… eine determinierte Folge ist.
In ai = u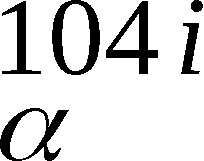 mit α3ɳ-2 geht fi ein:
u
mit α3ɳ-2 geht fi ein:
u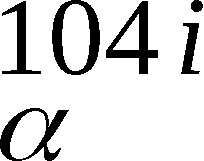 = u
= u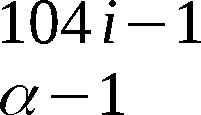 + r104i + s
+ r104i + s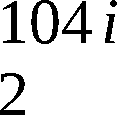 ∆ɳ + Tɳ(s
∆ɳ + Tɳ(s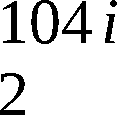 ,u
,u )
r104i = r52+52+104(i-1) = fi.
Aber fi und r104i-52, und geht deshalb schon in u
)
r104i = r52+52+104(i-1) = fi.
Aber fi und r104i-52, und geht deshalb schon in u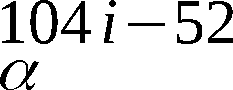 ein
und wirkt auf U104i-1.
Falls dieser Einfluß nicht beachtet wird, was durch die
Kompliziertheit der Ausdrücke Tɳ begründet werden kann,
erhält man eine analoge Situation:
Die statistischen Eigenschaften von (fi)i werden AL
übertragen.
Aus der Literatur ist bekannt, daß lineare rekurrente Folgen
über {0,1} mit Maximalperiode viele gute statistische
Eigenschaften besitzen.
Zum Beispiel unterscheiden sich die Verteilung der Häufig-
keiten von 0 und 1 und die Serienverteilung (Teilfolgen
gleicher Elemente) faktisch nicht von zufälligen gleich-
wahrscheinlichen Folgen.
Daher kann man damit rechnen, daß die Additionsreihen gute
statistische Eigenschaften besitzen.
3. Experimentelle Untersuchung der statistischen
Eigenschaften der Additionsreihe
Es wird ein Programm für eine EDVA erarbeitet, in dem die
in §2, Punkt 1 beschriebene kryptologische Schaltung
realisiert und die Additionsreihen AL=(ai)
ein
und wirkt auf U104i-1.
Falls dieser Einfluß nicht beachtet wird, was durch die
Kompliziertheit der Ausdrücke Tɳ begründet werden kann,
erhält man eine analoge Situation:
Die statistischen Eigenschaften von (fi)i werden AL
übertragen.
Aus der Literatur ist bekannt, daß lineare rekurrente Folgen
über {0,1} mit Maximalperiode viele gute statistische
Eigenschaften besitzen.
Zum Beispiel unterscheiden sich die Verteilung der Häufig-
keiten von 0 und 1 und die Serienverteilung (Teilfolgen
gleicher Elemente) faktisch nicht von zufälligen gleich-
wahrscheinlichen Folgen.
Daher kann man damit rechnen, daß die Additionsreihen gute
statistische Eigenschaften besitzen.
3. Experimentelle Untersuchung der statistischen
Eigenschaften der Additionsreihe
Es wird ein Programm für eine EDVA erarbeitet, in dem die
in §2, Punkt 1 beschriebene kryptologische Schaltung
realisiert und die Additionsreihen AL=(ai) erzeugt werden.
Aus ihnen werden einige statistische Zahlencharakteris-
tiken zum Zweck der Kontrolle der Zufälligkeit und Unabhän-
gigkeit der Additionsreihen berechnet.
Aus verschiedenen Gründen verzögert sich die Programm-
testung und -abarbeitung.
Die bisher erhaltenen Resultate geben keinerlei Hinweise
darauf, daß die Additionsreihen die statistischen Eigen-
schaften zufälliger gleichverteilter voneinander unab-
hängiger Folgen nicht besitzen.
KAPITEL V
Einschätzung der Sicherheit des Chiffrators
Einleitung
Im vorliegenden Kapitel werden einige grundlegende Methoden
der Bestimmung des schlüssel sowie einige Fragen der kryp-
tologischen Einschätzung von Fehlern in der Arbeit des
Systems und bei seiner Bedienung betrachtet.
Es werden die Bezeichnungen des vorigen Kapitels angewandt.
In den Fällen, in denen es notwendig ist, werden wir immer
(P,R) ∈ PR betrachten.
§1 Methoden der Bestimmung des Schlüssels
1. Wir betrachten folgendes Problem:
Der Dekrypteur kennt die kryptologische Schaltung, die
Langzeitschlüssel, das Schlüsselsystem, die Methode der
Herstellung der Schlüssel, die Gebrauchsanweisung des
Chiffrators und außerdem Additionsreihen (der Länge 47)
in beliebiger Anzahl.
Er muß den Schlüssel bestimmen. Es wird vorausgesetzt, daß
der Dekrypteur eine EDVA höchster Leitungsfähigkeit zur
Verfügung hat.
Im weiteren betrachten wir einige wichtige Teilaufgaben
dieser allgemeinen Problemstellung.
2. Wir betrachten die totale Probiermethode.
Wir berechnen die mittlere Zahl E1 der Elementar-Operationen
zur Bestimmung des Schlüssels, mit dem eine gewisse Gesamt-
heit gegebener Additionsreihen erzeugt wurde, von denen be-
kannt ist, daß sie ein- und demselben Schlüssel entsprechen.
Eine Elementaroperation[4.] entspricht der Arbeit, die zur
Realisierung eines Arbeitstaktes des Chiffrators (des
Übergangs Ui → Ui+1) auf der EDVA aufgewandt werden muß.
Wir nehmen an, daß die Arbeitsgeschwindigkeit der EDVA
1011 Elementaroperationen pro Sekunde oder 3*1018
Elementaroperationen pro Jahr beträgt.
Dann gilt E1 = |
erzeugt werden.
Aus ihnen werden einige statistische Zahlencharakteris-
tiken zum Zweck der Kontrolle der Zufälligkeit und Unabhän-
gigkeit der Additionsreihen berechnet.
Aus verschiedenen Gründen verzögert sich die Programm-
testung und -abarbeitung.
Die bisher erhaltenen Resultate geben keinerlei Hinweise
darauf, daß die Additionsreihen die statistischen Eigen-
schaften zufälliger gleichverteilter voneinander unab-
hängiger Folgen nicht besitzen.
KAPITEL V
Einschätzung der Sicherheit des Chiffrators
Einleitung
Im vorliegenden Kapitel werden einige grundlegende Methoden
der Bestimmung des schlüssel sowie einige Fragen der kryp-
tologischen Einschätzung von Fehlern in der Arbeit des
Systems und bei seiner Bedienung betrachtet.
Es werden die Bezeichnungen des vorigen Kapitels angewandt.
In den Fällen, in denen es notwendig ist, werden wir immer
(P,R) ∈ PR betrachten.
§1 Methoden der Bestimmung des Schlüssels
1. Wir betrachten folgendes Problem:
Der Dekrypteur kennt die kryptologische Schaltung, die
Langzeitschlüssel, das Schlüsselsystem, die Methode der
Herstellung der Schlüssel, die Gebrauchsanweisung des
Chiffrators und außerdem Additionsreihen (der Länge 47)
in beliebiger Anzahl.
Er muß den Schlüssel bestimmen. Es wird vorausgesetzt, daß
der Dekrypteur eine EDVA höchster Leitungsfähigkeit zur
Verfügung hat.
Im weiteren betrachten wir einige wichtige Teilaufgaben
dieser allgemeinen Problemstellung.
2. Wir betrachten die totale Probiermethode.
Wir berechnen die mittlere Zahl E1 der Elementar-Operationen
zur Bestimmung des Schlüssels, mit dem eine gewisse Gesamt-
heit gegebener Additionsreihen erzeugt wurde, von denen be-
kannt ist, daß sie ein- und demselben Schlüssel entsprechen.
Eine Elementaroperation[4.] entspricht der Arbeit, die zur
Realisierung eines Arbeitstaktes des Chiffrators (des
Übergangs Ui → Ui+1) auf der EDVA aufgewandt werden muß.
Wir nehmen an, daß die Arbeitsgeschwindigkeit der EDVA
1011 Elementaroperationen pro Sekunde oder 3*1018
Elementaroperationen pro Jahr beträgt.
Dann gilt E1 = | |*2*104.
Der Faktor |
|*2*104.
Der Faktor | | berücksichtigt, daß im Durchschnitt nach dem
(zufälligen) Probieren von |
| berücksichtigt, daß im Durchschnitt nach dem
(zufälligen) Probieren von | | Schlüsseln der richtige
gefunden wird.
Der Faktor 2 weist darauf hin, daß man im Durchschnitt
2 Zeichen der Additionsreihe erzeugen muß, um eine Entschei-
dung über die Richtigkeit des probierten Schlüssels zu
treffen.
Und der Faktor 104 wird deswegen gefordert, weil zur Erzeu-
gung eines Zeichens der Additionsreihe 104 Arbeitstakte des
Chiffrators erforderlich sind.
Das heißt:
E1 = s199*104 ≈ 6*1061
Folglich würde die EDVA durchschnittlich ca. 1043 Jahre
arbeiten, um den Schlüssel zu finden.
3. Wir betrachten jetzt die Probiermethode unter Beachtung der
Existenz von Klassen äquivalenter Schlüssel bezüglich der
Additionsreihe - Definition siehe Kapitel IV, §3, Einleitung
- gleicher Mächtigkeit K.
Wir bezeichnen mit E2 die mittlere Zahl der Elementar-
operationen, die zur Bestimmung des Schlüssels erforderlich sind.
Analog zum vorigen Punkt erhalten wir
E2 = |
| Schlüsseln der richtige
gefunden wird.
Der Faktor 2 weist darauf hin, daß man im Durchschnitt
2 Zeichen der Additionsreihe erzeugen muß, um eine Entschei-
dung über die Richtigkeit des probierten Schlüssels zu
treffen.
Und der Faktor 104 wird deswegen gefordert, weil zur Erzeu-
gung eines Zeichens der Additionsreihe 104 Arbeitstakte des
Chiffrators erforderlich sind.
Das heißt:
E1 = s199*104 ≈ 6*1061
Folglich würde die EDVA durchschnittlich ca. 1043 Jahre
arbeiten, um den Schlüssel zu finden.
3. Wir betrachten jetzt die Probiermethode unter Beachtung der
Existenz von Klassen äquivalenter Schlüssel bezüglich der
Additionsreihe - Definition siehe Kapitel IV, §3, Einleitung
- gleicher Mächtigkeit K.
Wir bezeichnen mit E2 die mittlere Zahl der Elementar-
operationen, die zur Bestimmung des Schlüssels erforderlich sind.
Analog zum vorigen Punkt erhalten wir
E2 = | |1/K * 2 * 104.
Der Faktor 1/K berücksichtigt, daß man aus jeder Klasse
äquivalenter Schlüssel nur einen Vertreter probieren muß.
Wir nehmen z.B. an, K ≈ 2120 ≈ 1036.
Dann gilt
E2 ≈ 5 * 1025.
Folglich würde die EDVA durchschnittlich ca. 107 Jahre arbeiten,
um den Schlüssel zu finden. Diese Zahl wird nicht wesentlich
gesenkt, wenn andere Varianten der Probiermethode benutzt
werden.
Wenn zum Beispiel dem Dekrypteur Additionsreihen zur Verfü-
gung stehen, die M verschiedene Schlüsseln entsprechen
(aber einem Langzeitschlüssel), so kann man
M ≤ 104
annehmen, da in 24 Stunden entweder 1 oder 2 Schlüssel ver-
wendet werden, und deshalb wird die Zahl M = 104 nicht früher
als nach ca 14 Jahren erreicht.
Vor allem die Größe K könnte die Sicherheit der Chiffrierab-
bildung wesentlich senken, wenn sie sehr große Werte annehmen
würde. Aber, worauf schon im Kapitel IV, §3, hingewiesen
wurde, gibt es dafür keinerlei Anhaltspunkte. Dasselbe trifft
auf den Fall der Existenz von Klassen äquivalenter Schlüssel
verschiedener Mächtigkeit zu.
4. Dekryptierung, wenn (u
|1/K * 2 * 104.
Der Faktor 1/K berücksichtigt, daß man aus jeder Klasse
äquivalenter Schlüssel nur einen Vertreter probieren muß.
Wir nehmen z.B. an, K ≈ 2120 ≈ 1036.
Dann gilt
E2 ≈ 5 * 1025.
Folglich würde die EDVA durchschnittlich ca. 107 Jahre arbeiten,
um den Schlüssel zu finden. Diese Zahl wird nicht wesentlich
gesenkt, wenn andere Varianten der Probiermethode benutzt
werden.
Wenn zum Beispiel dem Dekrypteur Additionsreihen zur Verfü-
gung stehen, die M verschiedene Schlüsseln entsprechen
(aber einem Langzeitschlüssel), so kann man
M ≤ 104
annehmen, da in 24 Stunden entweder 1 oder 2 Schlüssel ver-
wendet werden, und deshalb wird die Zahl M = 104 nicht früher
als nach ca 14 Jahren erreicht.
Vor allem die Größe K könnte die Sicherheit der Chiffrierab-
bildung wesentlich senken, wenn sie sehr große Werte annehmen
würde. Aber, worauf schon im Kapitel IV, §3, hingewiesen
wurde, gibt es dafür keinerlei Anhaltspunkte. Dasselbe trifft
auf den Fall der Existenz von Klassen äquivalenter Schlüssel
verschiedener Mächtigkeit zu.
4. Dekryptierung, wenn (u )i bekannt ist
Wir abstrahieren von der Realität, indem wir nicht nur die
Additionsreihe, sondern die gesamte Folge (u
)i bekannt ist
Wir abstrahieren von der Realität, indem wir nicht nur die
Additionsreihe, sondern die gesamte Folge (u )
) für hinreichend großes N als bekannt voraussetzen.
Von der Sicherheit der kryptologischen Schaltung unter
dieser starken Voraussetzung, kann man auf die Sicherheit
der kryptologischen Schaltung unter realen Bedingungen
schließen. Wir betrachten einige Varianten dieser Aufgabe
und damit verbundene Probleme.
4.1 Fast trivial ist der Fall, wenn die Folge (Ui)
für hinreichend großes N als bekannt voraussetzen.
Von der Sicherheit der kryptologischen Schaltung unter
dieser starken Voraussetzung, kann man auf die Sicherheit
der kryptologischen Schaltung unter realen Bedingungen
schließen. Wir betrachten einige Varianten dieser Aufgabe
und damit verbundene Probleme.
4.1 Fast trivial ist der Fall, wenn die Folge (Ui) bekannt
ist. In diesem Fall wird aufgrund der Gleichung
Ui = ϕ(s
bekannt
ist. In diesem Fall wird aufgrund der Gleichung
Ui = ϕ(s ,s
,s )Ui-1 (i=1,N)
und der Eineindeutigkeit von ϕ der Schlüssel S ∈
)Ui-1 (i=1,N)
und der Eineindeutigkeit von ϕ der Schlüssel S ∈  unmittelbar und ohne Benutzung einer EDVA bestimmt.
Eine völlig analoge Situation liegt vor, wenn die
Folge (2Ui)
unmittelbar und ohne Benutzung einer EDVA bestimmt.
Eine völlig analoge Situation liegt vor, wenn die
Folge (2Ui) bekannt ist; mit anderen Worten, wenn die
9 Folgen (u
bekannt ist; mit anderen Worten, wenn die
9 Folgen (u )
) , ɳ=1,9 bekannt sind.
Infolge 2Ui = 1Ui+1 betrachten wir des weiteren
nur die Folge (u
, ɳ=1,9 bekannt sind.
Infolge 2Ui = 1Ui+1 betrachten wir des weiteren
nur die Folge (u )
) .
4.2 Wir setzen die drei Folgen
(u
.
4.2 Wir setzen die drei Folgen
(u )
) , (u
, (u ')
') , (u
, (u '')
'') als bekannt voraus.
Seien ɳ'∈{R2,R3,R4,R5}, ɳ"∈{R6,R7,R8,R9},
ɳ' ≠ 1, ɳ" ≠ 1.
Dann werden S ∈
als bekannt voraus.
Seien ɳ'∈{R2,R3,R4,R5}, ɳ"∈{R6,R7,R8,R9},
ɳ' ≠ 1, ɳ" ≠ 1.
Dann werden S ∈ unmittelbar und ohne Benutzung einer
EDVA bestimmt. Tatsächlich, wir betrachten die Gleichungen
u
unmittelbar und ohne Benutzung einer
EDVA bestimmt. Tatsächlich, wir betrachten die Gleichungen
u = s
= s +ri+s
+ri+s ∆1+T1(s
∆1+T1(s ,u
,u ),
u
),
u = u
= u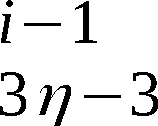 ' + ri+s
' + ri+s ∆ɳ'+Tɳ'(s
∆ɳ'+Tɳ'(s ,u
,u ),
u
),
u '' = u
'' = u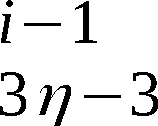 ''+ri+s
''+ri+s ∆ɳ''+Tɳ''(s
∆ɳ''+Tɳ''(s ,u
,u )
Zuerst wird s
)
Zuerst wird s aus der zweiten oder dritten Gleichung
bestimmt, was davon abhängt, ob Z(s
aus der zweiten oder dritten Gleichung
bestimmt, was davon abhängt, ob Z(s u
u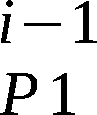 , …, u
, …, u )
von s
)
von s abhängt oder nicht. Und danach wird s
abhängt oder nicht. Und danach wird s aus der
ersten Gleichung bestimmt. Dieses Resultat weist darauf
hin, daß man aus der Kenntnis von nur zwei Folgen
aufgrund der Eigenschaften der Funktion Z im allgemeinen
nicht unmittelbar auf den Wert (s
aus der
ersten Gleichung bestimmt. Dieses Resultat weist darauf
hin, daß man aus der Kenntnis von nur zwei Folgen
aufgrund der Eigenschaften der Funktion Z im allgemeinen
nicht unmittelbar auf den Wert (s ,s
,s ) schließen
kann. Es weist auch darauf hin, daß es nicht gleichgültig
ist, welche Folge gerade bekannt sind.
4.3 Wir gehen von einer anderen Seite an das Problem heran.
Wir setzen für Festes S zwei Folgen (u
) schließen
kann. Es weist auch darauf hin, daß es nicht gleichgültig
ist, welche Folge gerade bekannt sind.
4.3 Wir gehen von einer anderen Seite an das Problem heran.
Wir setzen für Festes S zwei Folgen (u )
) und (u
und (u ')
') die F ∈
die F ∈  beziehungsweise F' ∈
beziehungsweise F' ∈  , F ≠ F', entsprechend,
als bekannt voraus.
Wir betrachten die Gleichungen
u
, F ≠ F', entsprechend,
als bekannt voraus.
Wir betrachten die Gleichungen
u = s
= s +ri + s
+ri + s (Z1(u
(Z1(u ) + ∆1)+
) + ∆1)+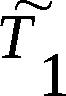 (u
(u ),
u
),
u ' = s
' = s +ri' + s
+ri' + s (Z1(u
(Z1(u )') + ∆1)+
)') + ∆1)+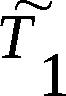 (u
(u ')
dabei wird
T1(s
')
dabei wird
T1(s ,u
,u ) = s
) = s Z1(u
Z1(u ) +
) + 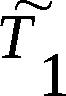 (u
(u )
bezeichnet und für u
)
bezeichnet und für u ' entsprechend.
Sofort ist klar, daß das Paar (s
' entsprechend.
Sofort ist klar, daß das Paar (s , s
, s ) eindeutig
genau dann nicht bestimmt werden kann, wenn
Z1(u
) eindeutig
genau dann nicht bestimmt werden kann, wenn
Z1(u ) = Z1(u
) = Z1(u ') = ∆1,
das heißt, im Durchschnitt in einem der vier Fälle.
In diesem Fall ist s
') = ∆1,
das heißt, im Durchschnitt in einem der vier Fälle.
In diesem Fall ist s eindeutig, aber s
eindeutig, aber s läßt beide
Werte 0 und 1 zu, wieder aufgrund der Eigenschaft der
Funktion Z.
Im Durchschnitt werden drei Viertel aller Paare (s
läßt beide
Werte 0 und 1 zu, wieder aufgrund der Eigenschaft der
Funktion Z.
Im Durchschnitt werden drei Viertel aller Paare (s ,s
,s )
eindeutig bestimmt und ein Paar läßt zwei Werte zu.
Für N = 104 erhalten wir deshalb im Durchschnitt 21/4*104
= 226 ≈ 6*107 Schlüssel.
Diese Zahl wird nicht viel kleiner, wenn wir nur die
S ∈
)
eindeutig bestimmt und ein Paar läßt zwei Werte zu.
Für N = 104 erhalten wir deshalb im Durchschnitt 21/4*104
= 226 ≈ 6*107 Schlüssel.
Diese Zahl wird nicht viel kleiner, wenn wir nur die
S ∈ ≠
≠  berücksichtigen. Sie ist geringfügig im Vergleich
zu |
berücksichtigen. Sie ist geringfügig im Vergleich
zu | |. Man kann annehmen, daß sie sich weiter wesentlich
verkleinert, wenn drei oder mehr Folgen bekannt sind, die
paarweise verschiedenen F ∈
|. Man kann annehmen, daß sie sich weiter wesentlich
verkleinert, wenn drei oder mehr Folgen bekannt sind, die
paarweise verschiedenen F ∈  entsprechen.
Somit: Wenn hinreichend viele Folgen (u
entsprechen.
Somit: Wenn hinreichend viele Folgen (u )
) bekannt
sind, die ein- und demselben S ∈
bekannt
sind, die ein- und demselben S ∈  entsprechen, kann man
S eindeutig bestimmen. Die Methode der Bestimmung von S folgen
aus den oben gezeigten Überlegungen. Sie ist in der Praxis
ohne EDVA durchführbar.
Wenn einige Folgen (u
entsprechen, kann man
S eindeutig bestimmen. Die Methode der Bestimmung von S folgen
aus den oben gezeigten Überlegungen. Sie ist in der Praxis
ohne EDVA durchführbar.
Wenn einige Folgen (u )
) für ɳ≠1 bekannt sind, werden
die Gleichungen komplizierter, aber das Endresultat bleibt
das gleiche.
4.4 Wenn nur eine Folge (u
für ɳ≠1 bekannt sind, werden
die Gleichungen komplizierter, aber das Endresultat bleibt
das gleiche.
4.4 Wenn nur eine Folge (u )
) ɳ ∈ 1,9
bekannt ist, ist es unmöglich, S unmittelbar zu bestimmen.
Betrachten wir zuerst (u
ɳ ∈ 1,9
bekannt ist, ist es unmöglich, S unmittelbar zu bestimmen.
Betrachten wir zuerst (u )
) und finden die Teilmenge
und finden die Teilmenge
 * aller S ∈
* aller S ∈  , die für gegebenes F dieser Folge erzeugen.
Die Größe u
, die für gegebenes F dieser Folge erzeugen.
Die Größe u wurde durch folgende Formel bestimmt
(4.1)
u
wurde durch folgende Formel bestimmt
(4.1)
u = s
= s .+ri+s
.+ri+s ∆1+T1(s
∆1+T1(s ,u
,u )
Wir bezeichnen mit ∑n = {δn} die Menge aller Tupel
δn =((s
)
Wir bezeichnen mit ∑n = {δn} die Menge aller Tupel
δn =((s ,s
,s ),(s
),(s ,s
,s ), …, (s
), …, (s ,s
,s )) ∈ {0,1}2n,
die der Formel für i=1,n genügen.
Es ist leicht zu sehen, daß |∑1|=2 ist.
Für festes ρn ist der Vektor Un ebenfalls fest, aber dann
erhält man aus der Gleichung (4.1) genau zwei Lösungen
(s
)) ∈ {0,1}2n,
die der Formel für i=1,n genügen.
Es ist leicht zu sehen, daß |∑1|=2 ist.
Für festes ρn ist der Vektor Un ebenfalls fest, aber dann
erhält man aus der Gleichung (4.1) genau zwei Lösungen
(s +1,s
+1,s +1). Deshalb ist |∑n+2| = 2|∑n|,
woraus folgt |∑n| = 2n für n ≤ 104.
Das heißt |∑104| = |
+1). Deshalb ist |∑n+2| = 2|∑n|,
woraus folgt |∑n| = 2n für n ≤ 104.
Das heißt |∑104| = | *| = 2104 ≈ 1032.
Wenn wir nur S ∈
*| = 2104 ≈ 1032.
Wenn wir nur S ∈  zulassen, so sinkt diese Zahl wenig.
Aber diese Zahl weiter zu verringern, ist auf keine Weise
möglich, wenn wir nicht neue Informationen hinzufügen.
Man muß zum Fall N > 104 übergehen.
Für N > 104 kann man die Gleichung
s
zulassen, so sinkt diese Zahl wenig.
Aber diese Zahl weiter zu verringern, ist auf keine Weise
möglich, wenn wir nicht neue Informationen hinzufügen.
Man muß zum Fall N > 104 übergehen.
Für N > 104 kann man die Gleichung
s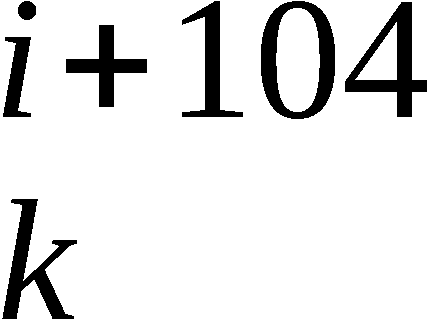 = s
= s (k = 1,2; i = 1,2, …) ausnutzen.
Für festes δ104 ∈
(k = 1,2; i = 1,2, …) ausnutzen.
Für festes δ104 ∈  * ist der Vektor U104 auch fest, und
dann ergeben sich aus der Gleichung (4.1) genau zwei
Lösungen (s
* ist der Vektor U104 auch fest, und
dann ergeben sich aus der Gleichung (4.1) genau zwei
Lösungen (s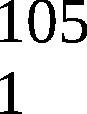 ,s
,s ). Entweder stimmt keine der beiden
mit (s
). Entweder stimmt keine der beiden
mit (s s
s ) überein, oder eine. Im ersten Fall muß man δ1
aus der Menge
) überein, oder eine. Im ersten Fall muß man δ1
aus der Menge  * entfernen, im zweiten Fall muß man∑104
in
* entfernen, im zweiten Fall muß man∑104
in  * lassen. Wenn δ104 nicht der richtige Schlüssel
ist, so kann man annehmen, daß im Durchschnitt beide Fälle
gleich oft eintreten. Das würde bedeuten, daß in diesem
Schritt
* lassen. Wenn δ104 nicht der richtige Schlüssel
ist, so kann man annehmen, daß im Durchschnitt beide Fälle
gleich oft eintreten. Das würde bedeuten, daß in diesem
Schritt  * im Durchschnitt auf die Hälfte verringert wird.
Analog erhielten wir, indem wir bis N = 208 fortsetzten,
im Durchschnitt
|
* im Durchschnitt auf die Hälfte verringert wird.
Analog erhielten wir, indem wir bis N = 208 fortsetzten,
im Durchschnitt
| *| = 1/2104 * (Σ104) = 1.
Das heißt, im Durchschnitt kann man aus (u
*| = 1/2104 * (Σ104) = 1.
Das heißt, im Durchschnitt kann man aus (u )
) S eindeutig
bestimmen.
Wir bemerken, daß man in der Praxis diesen Weg nicht
realisieren kann, da man ≈1032 paarweise verschiedener
Schlüssel S ∈
S eindeutig
bestimmen.
Wir bemerken, daß man in der Praxis diesen Weg nicht
realisieren kann, da man ≈1032 paarweise verschiedener
Schlüssel S ∈  * berechnen, speichern und abarbeiten muß.
Die Situation wird noch komplizierter, wenn (u
* berechnen, speichern und abarbeiten muß.
Die Situation wird noch komplizierter, wenn (u )
) für ɳ≠ 1 betrachtet wird. in diesem Fall geht
s
für ɳ≠ 1 betrachtet wird. in diesem Fall geht
s nicht in die Bestimmung von u
nicht in die Bestimmung von u ein.
5. Bemerkungen zur analytischen Dekryptiermethode
Wir setzen die Additionsreihen
A47 = Ψ47(U,S,F)
für alle F ∈
ein.
5. Bemerkungen zur analytischen Dekryptiermethode
Wir setzen die Additionsreihen
A47 = Ψ47(U,S,F)
für alle F ∈  bei festem Schlüssel S ∈
bei festem Schlüssel S ∈  als bekannt
voraus. Die Aufgabe besteht in der Ermittlung von S mit
der Methode der Lösung des Gleichungssystems
A
als bekannt
voraus. Die Aufgabe besteht in der Ermittlung von S mit
der Methode der Lösung des Gleichungssystems
A = Ψ47(U,S,Fi), i = 1,252.
Das System ist nichtlinear mit 208 Unbekannten und
47 - 252 Gleichungen. Vergleicht man die Anzahl der
Unbekannten mit der Anzahl der Gleichungen, so kann man
vermuten, daß die Lösung eindeutig ist. Man kann weiter
vermuten, daß einige Gleichungen Unbekannte in linearer Form
haben, was zur schrittweisen Verringerung der Anzahl der
Unbekannten ausnutzbar ist. Aufgrund der Kompliziertheit der
Abbildung Φ muß man jedoch die Aufstellung der Gleichungen
und ihrer Anwendung als in der Praxis nicht realisierbar
bezeichnen. Siehe auch Kap. IV, §2, 4.
§2 Kryptologische Auswirkungen technischer Fehler1)
1. Allgemeine Aussagen über technische Fehler
___
1) In diesem und dem folgenden Paragraphen werden die Bezeich-
nungen der Kapitel I - III genutzt.
In der Chiffriereinrichtung der Station C können aus
technischer Sicht folgende Fehler während des Betriebes
auftreten:
(a) Ausfall elektronischer Bauelemente
(b) Leitungsbruch auf gedruckten Leiterplatten
(c) Kalte Lötstelle
(d) Ausfall von Wickelverbindungen
(e) Unterbrechung des Kontaktes zwischen Leiterplatte und
Verdrahtung (Kontakt Steckerleiste - Steckverbinder)
(f) Drahtbruch in der Verdrahtung.
Die Einschätzung der Funktionssicherheit der Bauelemente wird
durch die Angabe von Ausfallraten λ gegeben. Zur Funktions-
sicherheit der Bauelemente und der Baugruppen in den serien-
mäßig zu produzierenden Anlagen sind zur Zeit keine quantita-
tiven Aussagen möglich. Bei der Erprobung des Labormusters
der Anlage OPERATION traten keine technischen Fehler oben
angegebener Art auf. Schlußfolgerungen auf die serienmäßig
produzierten Anlagen können daraus jedoch nicht abgeleitet
werden.
Im Entwicklungsinstitut IfR wird zur Zeit angenommen,
daß unter Laborbedingungen für die oben angegebenen Fehler
folgende Ausfallraten λ zutreffen (λ = a * 10-6 * n-1):
(a) a = 0,01 (je KME-10- Schaltkreis)
(b) a = 0,5 (je doppelt kaschierter Leiterplatte gesamt)
(c) a = 0,01 (je Lötstelle)
(d) a = 0,001 (je Wickelverbindung)
(e) a = 0,05 (je Kontakt).
Zu (f) existieren keine Angaben.
Funktionell gesehen, gehören die angegebenen Fehlermöglich-
keiten zu zwei verschiedenen Klassen.
Zur ersten Klasse gehört (1). Technische Fehler der Art (1)
sind in ihren Auswirkungen relativ unbestimmt.
Zur zweiten Klasse gehören die Arten (b)-(e). Als
Folge dieser Fehler werden konstante L-Folgen erzeugt.
2. Technische Fehler im Chiffrator und bei der Verarbeitung
der Folge W
Im Chiffrator und Prüf-Chiffrator werden folgende Signale
verarbeitet (s. Kap. III, Abb. 3.2):
FU, t104, tR, S = (S1,S2).
Es wird jetzt vorausgesetzt, daß alle diese Signale richtig
am Eingang des Chiffrators und des Prüf-Chiffrators anliegen.
weiter wird vorausgesetzt, daß durch den Prüfbaustein P-W+KT2
Die Blockierung des Geheimtextausganges der Chiffriereinrich-
tung (Öffnung Schalter S3 oder/und S4 kurz: Blockierung) aus-
gelöst wird, wenn sich die Ausgänge der Additionselemente A1
und A2 in der Verschlüsselungsbaugruppe V unterscheiden.
Unter diesen Voraussetzungen führt ein technische Fehler
gleich welcher Art im Chiffrator oder bei der Verarbeitung
der Folge Wi (Linie Ausgang Chiffrator bis Ausgang A1) nur
dann nicht zur Blockierung, wenn ein in seiner Wirkung
gleicher Fehler gleichzeitig oder nahezu gleichzeitig
(Zeiteinheit ∆t)1) parallel auch im Prüf-Chiffrator oder
bei der Verarbeitung der Folge Wi-P (Linie Ausgang Prüf-
Chiffrator bis Ausgang A2) auftritt.
Die Wahrscheinlichkeit, daß in parallelen, sich nicht gegen-
seitig beeinflussenden Baugruppen gleichzeitig oder nahezu
gleichzeitig der gleiche Fehler auftritt, ist sehr gering,
auch wenn man beachtet, daß gewisse Abhängigkeiten gleicher
Baugruppen durch die Produktion vorhanden sein können
___
1) Vom Bedienpult der Anlage kann durch das Signal BO die
Blockierung aufgehoben werden. Wenn in der Zeit zwischen
Blockierung und dem Signal BO in der parallelen Baugruppe der
gleiche Fehler auftritt, erfolgt keine weitere Blockierung.
Der Zeitraum ∆t muß somit aus kryptologischer Sicht bestimmt
werden. Mit der Festlegung von ∆t wird gefordert, daß bei
Auftreten des Fehlersignals M4-CE zum Zeitpunkt t, letztmalig
zum Zeitpunkt t + ∆t BO gegeben wird, wenn nach vorherigen
BO M4-CE nicht gelöscht worden ist.
Wenn bei diesem letzten BO M4-CE nicht gelöscht worden ist,
muß eine Überprüfung der Chiffriereinrichtung erfolgen.
3. Kryptologisch schlechte Folgen FU im Chiffrator
3.1 Technische Fehler bei der Erzeugung von FU
Kryptologisch von Bedeutung sind die Fehler, die zu einer
Folge FU mit kurzer Periode gleichzeitig am Eingang des
Chiffrators und des Prüf-Chiffrators führen. Wenn FU kurz-
periodisch ist, so besteht die Möglichkeit der Benutzung
gleicher Additionsreihen der Länge 47 zur Chiffrierung ver-
schiedener Grundtextblöcke. Speziell wenn FU die Periode 1 hat,
wird zur Chiffrierung aller Grundtexte die gleiche Additions-
reihe hergestellt im Chiffrator.
In Abbildung 3.2 im Kapitel III sind schematisch die Erzeugung
der Folge F und der Folge FU und die entsprechenden Prüfungen
dargestellt.
Es wird jetzt vorausgesetzt, daß die Blockierung anspricht,
wenn
(a) in P-ZG/F eine Folge mit einem konstanten Abschnitt
der Länge ≥ 56 eingegeben wird;
(b) in P-FU oder/und P-FU-P im i-ten Übertragungstakt
TÜi (i=1,2,…) eine konstante Folge eingegeben wird,
(c) sich die in FG1 und FG2 erzeugten Folgen F, die in P-F
verglichen werden, unterscheiden;
(d) sich die vom Chiffrator und Prüf-Chiffrator erzeugten
Folgen W und W-P unterscheiden.
Anhand Abbildung 3.2, im Kapitel III ist zu erkennen, daß un-
ter dieser Voraussetzung nur dann im Chiffrator und im Prüf-
Chiffrator die gleichen kurzperiodischen Folgen FU, FU-P verarbeitet
werden, ohne daß die Blockierung anspricht, wenn
(a) in FG1 und in FG2 gleichzeitig oder nahezu gleichzeitig
(Zeiteinheit ∆t) auftretender Fehler gleiche kurzperio-
dische nichtkonstante Folgen F erzeugt werden;
(b) gleichzeitig oder nahezu gleichzeitig (Zeiteinheit ∆t)
die Leitung FUi-P nach der Abzweigung für P-FU-P und die
Leitung FUi nach der Abzweigung für P-FU unterbrochen
wird.
Die Wahrscheinlichkeit dieses Ereignis ist sehr gering.
3.2 Wahrscheinlichkeit gleicher F-Folgen-Abschnitte im
Ergebnis von Stromunterbrechungen
Die Anlage OPERATION arbeitet im Dauerbetrieb. Nur dann,
wenn die Prüftaste zur Kontrolle von Ü-ZG/F und A3 gedrückt
wird (s. Punkt 6 dieses Paragraphen) oder wenn der Strom
aufgrund technischer Fehler ausfällt [oder wenn in der An-
lage ein (systematischer) Fehler auftritt, zu dessen Besei-
tigung der Strom ausgeschaltet wird], wird die Erzeugung der
Folge F unterbrochen. Über die Häufigkeit solcher Unter-
brechungen ist zur Zeit keine Aussage möglich.
Wenn während der Geltungsdauer eines Schlüssels S (Kurzzeit-
schlüssel) eine Unterbrechung der Erzeugung von F erfolgt,
besteht die Möglichkeit, daß nach Wiedereinschalten des Stro-
mes eine Folge F erzeugt wird, die mit der vor der Unter-
brechung erzeugten Folge F phasengleich ist. Damit entsteht
die Möglichkeit der Erzeugung gleicher Additionsreihen zur
Chiffrierung unterschiedlicher Grundtextblöcke.
Unter der Voraussetzung, daß der Zufallsgenerator ZG eine
hinreichend zufällige Folge erzeugt und die Geltungsdauer
des Kurzzeitschlüssels S nicht größer als eine Woche ist,
ist die Wahrscheinlichkeit für eine Übereinstimmung der nach
einer Unterbrechung erzeugten Folge F mit einem Abschnitt
der bei gleichem S gesamten vorher erzeugten Folge F kleiner
als
= Ψ47(U,S,Fi), i = 1,252.
Das System ist nichtlinear mit 208 Unbekannten und
47 - 252 Gleichungen. Vergleicht man die Anzahl der
Unbekannten mit der Anzahl der Gleichungen, so kann man
vermuten, daß die Lösung eindeutig ist. Man kann weiter
vermuten, daß einige Gleichungen Unbekannte in linearer Form
haben, was zur schrittweisen Verringerung der Anzahl der
Unbekannten ausnutzbar ist. Aufgrund der Kompliziertheit der
Abbildung Φ muß man jedoch die Aufstellung der Gleichungen
und ihrer Anwendung als in der Praxis nicht realisierbar
bezeichnen. Siehe auch Kap. IV, §2, 4.
§2 Kryptologische Auswirkungen technischer Fehler1)
1. Allgemeine Aussagen über technische Fehler
___
1) In diesem und dem folgenden Paragraphen werden die Bezeich-
nungen der Kapitel I - III genutzt.
In der Chiffriereinrichtung der Station C können aus
technischer Sicht folgende Fehler während des Betriebes
auftreten:
(a) Ausfall elektronischer Bauelemente
(b) Leitungsbruch auf gedruckten Leiterplatten
(c) Kalte Lötstelle
(d) Ausfall von Wickelverbindungen
(e) Unterbrechung des Kontaktes zwischen Leiterplatte und
Verdrahtung (Kontakt Steckerleiste - Steckverbinder)
(f) Drahtbruch in der Verdrahtung.
Die Einschätzung der Funktionssicherheit der Bauelemente wird
durch die Angabe von Ausfallraten λ gegeben. Zur Funktions-
sicherheit der Bauelemente und der Baugruppen in den serien-
mäßig zu produzierenden Anlagen sind zur Zeit keine quantita-
tiven Aussagen möglich. Bei der Erprobung des Labormusters
der Anlage OPERATION traten keine technischen Fehler oben
angegebener Art auf. Schlußfolgerungen auf die serienmäßig
produzierten Anlagen können daraus jedoch nicht abgeleitet
werden.
Im Entwicklungsinstitut IfR wird zur Zeit angenommen,
daß unter Laborbedingungen für die oben angegebenen Fehler
folgende Ausfallraten λ zutreffen (λ = a * 10-6 * n-1):
(a) a = 0,01 (je KME-10- Schaltkreis)
(b) a = 0,5 (je doppelt kaschierter Leiterplatte gesamt)
(c) a = 0,01 (je Lötstelle)
(d) a = 0,001 (je Wickelverbindung)
(e) a = 0,05 (je Kontakt).
Zu (f) existieren keine Angaben.
Funktionell gesehen, gehören die angegebenen Fehlermöglich-
keiten zu zwei verschiedenen Klassen.
Zur ersten Klasse gehört (1). Technische Fehler der Art (1)
sind in ihren Auswirkungen relativ unbestimmt.
Zur zweiten Klasse gehören die Arten (b)-(e). Als
Folge dieser Fehler werden konstante L-Folgen erzeugt.
2. Technische Fehler im Chiffrator und bei der Verarbeitung
der Folge W
Im Chiffrator und Prüf-Chiffrator werden folgende Signale
verarbeitet (s. Kap. III, Abb. 3.2):
FU, t104, tR, S = (S1,S2).
Es wird jetzt vorausgesetzt, daß alle diese Signale richtig
am Eingang des Chiffrators und des Prüf-Chiffrators anliegen.
weiter wird vorausgesetzt, daß durch den Prüfbaustein P-W+KT2
Die Blockierung des Geheimtextausganges der Chiffriereinrich-
tung (Öffnung Schalter S3 oder/und S4 kurz: Blockierung) aus-
gelöst wird, wenn sich die Ausgänge der Additionselemente A1
und A2 in der Verschlüsselungsbaugruppe V unterscheiden.
Unter diesen Voraussetzungen führt ein technische Fehler
gleich welcher Art im Chiffrator oder bei der Verarbeitung
der Folge Wi (Linie Ausgang Chiffrator bis Ausgang A1) nur
dann nicht zur Blockierung, wenn ein in seiner Wirkung
gleicher Fehler gleichzeitig oder nahezu gleichzeitig
(Zeiteinheit ∆t)1) parallel auch im Prüf-Chiffrator oder
bei der Verarbeitung der Folge Wi-P (Linie Ausgang Prüf-
Chiffrator bis Ausgang A2) auftritt.
Die Wahrscheinlichkeit, daß in parallelen, sich nicht gegen-
seitig beeinflussenden Baugruppen gleichzeitig oder nahezu
gleichzeitig der gleiche Fehler auftritt, ist sehr gering,
auch wenn man beachtet, daß gewisse Abhängigkeiten gleicher
Baugruppen durch die Produktion vorhanden sein können
___
1) Vom Bedienpult der Anlage kann durch das Signal BO die
Blockierung aufgehoben werden. Wenn in der Zeit zwischen
Blockierung und dem Signal BO in der parallelen Baugruppe der
gleiche Fehler auftritt, erfolgt keine weitere Blockierung.
Der Zeitraum ∆t muß somit aus kryptologischer Sicht bestimmt
werden. Mit der Festlegung von ∆t wird gefordert, daß bei
Auftreten des Fehlersignals M4-CE zum Zeitpunkt t, letztmalig
zum Zeitpunkt t + ∆t BO gegeben wird, wenn nach vorherigen
BO M4-CE nicht gelöscht worden ist.
Wenn bei diesem letzten BO M4-CE nicht gelöscht worden ist,
muß eine Überprüfung der Chiffriereinrichtung erfolgen.
3. Kryptologisch schlechte Folgen FU im Chiffrator
3.1 Technische Fehler bei der Erzeugung von FU
Kryptologisch von Bedeutung sind die Fehler, die zu einer
Folge FU mit kurzer Periode gleichzeitig am Eingang des
Chiffrators und des Prüf-Chiffrators führen. Wenn FU kurz-
periodisch ist, so besteht die Möglichkeit der Benutzung
gleicher Additionsreihen der Länge 47 zur Chiffrierung ver-
schiedener Grundtextblöcke. Speziell wenn FU die Periode 1 hat,
wird zur Chiffrierung aller Grundtexte die gleiche Additions-
reihe hergestellt im Chiffrator.
In Abbildung 3.2 im Kapitel III sind schematisch die Erzeugung
der Folge F und der Folge FU und die entsprechenden Prüfungen
dargestellt.
Es wird jetzt vorausgesetzt, daß die Blockierung anspricht,
wenn
(a) in P-ZG/F eine Folge mit einem konstanten Abschnitt
der Länge ≥ 56 eingegeben wird;
(b) in P-FU oder/und P-FU-P im i-ten Übertragungstakt
TÜi (i=1,2,…) eine konstante Folge eingegeben wird,
(c) sich die in FG1 und FG2 erzeugten Folgen F, die in P-F
verglichen werden, unterscheiden;
(d) sich die vom Chiffrator und Prüf-Chiffrator erzeugten
Folgen W und W-P unterscheiden.
Anhand Abbildung 3.2, im Kapitel III ist zu erkennen, daß un-
ter dieser Voraussetzung nur dann im Chiffrator und im Prüf-
Chiffrator die gleichen kurzperiodischen Folgen FU, FU-P verarbeitet
werden, ohne daß die Blockierung anspricht, wenn
(a) in FG1 und in FG2 gleichzeitig oder nahezu gleichzeitig
(Zeiteinheit ∆t) auftretender Fehler gleiche kurzperio-
dische nichtkonstante Folgen F erzeugt werden;
(b) gleichzeitig oder nahezu gleichzeitig (Zeiteinheit ∆t)
die Leitung FUi-P nach der Abzweigung für P-FU-P und die
Leitung FUi nach der Abzweigung für P-FU unterbrochen
wird.
Die Wahrscheinlichkeit dieses Ereignis ist sehr gering.
3.2 Wahrscheinlichkeit gleicher F-Folgen-Abschnitte im
Ergebnis von Stromunterbrechungen
Die Anlage OPERATION arbeitet im Dauerbetrieb. Nur dann,
wenn die Prüftaste zur Kontrolle von Ü-ZG/F und A3 gedrückt
wird (s. Punkt 6 dieses Paragraphen) oder wenn der Strom
aufgrund technischer Fehler ausfällt [oder wenn in der An-
lage ein (systematischer) Fehler auftritt, zu dessen Besei-
tigung der Strom ausgeschaltet wird], wird die Erzeugung der
Folge F unterbrochen. Über die Häufigkeit solcher Unter-
brechungen ist zur Zeit keine Aussage möglich.
Wenn während der Geltungsdauer eines Schlüssels S (Kurzzeit-
schlüssel) eine Unterbrechung der Erzeugung von F erfolgt,
besteht die Möglichkeit, daß nach Wiedereinschalten des Stro-
mes eine Folge F erzeugt wird, die mit der vor der Unter-
brechung erzeugten Folge F phasengleich ist. Damit entsteht
die Möglichkeit der Erzeugung gleicher Additionsreihen zur
Chiffrierung unterschiedlicher Grundtextblöcke.
Unter der Voraussetzung, daß der Zufallsgenerator ZG eine
hinreichend zufällige Folge erzeugt und die Geltungsdauer
des Kurzzeitschlüssels S nicht größer als eine Woche ist,
ist die Wahrscheinlichkeit für eine Übereinstimmung der nach
einer Unterbrechung erzeugten Folge F mit einem Abschnitt
der bei gleichem S gesamten vorher erzeugten Folge F kleiner
als  4. Ausfall des Taktes t104 im Chiffrator und im Prüf-Chiffrator
Bei Ausfall des Taktes t104 im Chiffrator ändert sich der
innere Zustand im Chiffrator nicht, d.h. der Inhalt des
Speicherelements UP29 vom Speicher U ändert sich nicht.
Es entstehen somit nur Additionsreihen identisch 0 (oder
identisch 1).
Es wird jetzt vorausgesetzt, daß mindestens zwei der drei
Prüfbausteine P-W, P-W-P und P-W ⊕ KT2 beim Auftreten
entsprechender Fehler die Blockierung auslöst. Unter dieser
Voraussetzung führt der Ausfall von t104 im Chiffrator
oder/und im Prüf-Chiffrator immer zur Blockierung. Wenn der
Takt t104 ausfällt aufgrund des Ausfalls von T350 oder/und
FGFU in der Schlüsseleingabeeinheit, dann wird das im Prüf-
baustein P-t104 erkannt.
5. Verarbeitung fehlerhafter Schlüssel S
Wenn im Chiffrator ein Schlüssel S = (S1,S2) verarbeitet
wird, der nicht mit dem auf der Schlüssellochkarte gespei-
cherten Schlüssel übereinstimmt, so entstehen keine krypto-
logisch schlechten Additionsreihen. Es wird vorausgesetzt,
daß für den Dekrypteur erkennbar ist, wenn die Station C und
speziell die Chiffriereinrichtung fehlerhaft arbeitet.
Es bleibt für ihn die Möglichkeit zu probieren, die
verschiedenen möglichen Fehlervarianten zur Dekryp-
tierung zu nutzen.
In Bezug auf die Verarbeitung des Schlüssels S im Chiffra-
tor ist die Möglichkeit der Nutzung solcher Fehler, die dazu
führen, daß eine oder beide der im Chiffrator verarbeiteten
Komponenten S1, S2 des Schlüssels identisch 0 oder identisch
1 ist, real.
Im Prüfbaustein P-S1/S2 wir überprüft, ob die Bedingung
4. Ausfall des Taktes t104 im Chiffrator und im Prüf-Chiffrator
Bei Ausfall des Taktes t104 im Chiffrator ändert sich der
innere Zustand im Chiffrator nicht, d.h. der Inhalt des
Speicherelements UP29 vom Speicher U ändert sich nicht.
Es entstehen somit nur Additionsreihen identisch 0 (oder
identisch 1).
Es wird jetzt vorausgesetzt, daß mindestens zwei der drei
Prüfbausteine P-W, P-W-P und P-W ⊕ KT2 beim Auftreten
entsprechender Fehler die Blockierung auslöst. Unter dieser
Voraussetzung führt der Ausfall von t104 im Chiffrator
oder/und im Prüf-Chiffrator immer zur Blockierung. Wenn der
Takt t104 ausfällt aufgrund des Ausfalls von T350 oder/und
FGFU in der Schlüsseleingabeeinheit, dann wird das im Prüf-
baustein P-t104 erkannt.
5. Verarbeitung fehlerhafter Schlüssel S
Wenn im Chiffrator ein Schlüssel S = (S1,S2) verarbeitet
wird, der nicht mit dem auf der Schlüssellochkarte gespei-
cherten Schlüssel übereinstimmt, so entstehen keine krypto-
logisch schlechten Additionsreihen. Es wird vorausgesetzt,
daß für den Dekrypteur erkennbar ist, wenn die Station C und
speziell die Chiffriereinrichtung fehlerhaft arbeitet.
Es bleibt für ihn die Möglichkeit zu probieren, die
verschiedenen möglichen Fehlervarianten zur Dekryp-
tierung zu nutzen.
In Bezug auf die Verarbeitung des Schlüssels S im Chiffra-
tor ist die Möglichkeit der Nutzung solcher Fehler, die dazu
führen, daß eine oder beide der im Chiffrator verarbeiteten
Komponenten S1, S2 des Schlüssels identisch 0 oder identisch
1 ist, real.
Im Prüfbaustein P-S1/S2 wir überprüft, ob die Bedingung
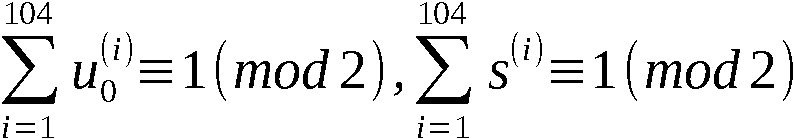 erfüllt ist. Diese Bedingung ist nicht erfüllt, wenn S1
oder S2 identisch 0 oder identisch 1 ist.
Unter der Voraussetzung, daß bei S1 const. oder S2 const.
in P-S1/S2 die Blockierung ausgelöst wird (M4-SE = 1),
entstehen nicht erkennbare Fehler oben erwähnter Art nur dann, wenn zu-
gleich oder nahezu zugleich (Zeiteinheit ∆t) die Verbindung
Verzweigungspunkt G oder/und H Chiffrator und die Verbindung
Verzweigungspunkt G oder/und H Prüf-Chiffrator unterbrochen
werden. Die Wahrscheinlichkeit solcher gleichzeitig oder nahe-
zu gleichzeitig (Zeiteinheit ∆t) auftretender Fehler ist
sehr gering.
6. Technische Fehler in den Prüfbaugruppen, -bausteinen
und Baugruppen B1, B2
Kryptologisch sind nur die technischen Fehler von Bedeu-
tung, die selbst nicht zur Blockierung führen und es über
dies zulassen, daß bei auftretenden Fehlern in den anderen
Baugruppen keine Blockierung der Chiffriereinrichtung aus-
gelöst wird.
Fehler dieser Art sind im normalen Betrieb der Anlage nicht
sofort erkennbar. Sie können sich bemerkbar machen durch
Ausfall des gesamten Systems, wenn zusätzlich ein entsprechen-
der Fehler bei der Bildung des Geheimtextes auftritt (alle
Stationen E können die empfangenen Nachrichten nicht mehr
dechiffrieren).
Die Prüfbausteine (außer P-t104) bestehen nur aus wenigen
Bauelementen (maximal 3 Schaltkreise vom Typ KME-10).
Für die Funktionsfähigkeit der Prüfbaugruppen, -bausteine
und von B1, B2 ist ihre Taktung mit dem Übertragungstakt TÜ
(Abfrage des Prüfergebnisses) notwendig (außer P-F und
P-W ⊕ KT2).
Die Taktführung ist so gestaltet (TÜ1 und TÜ2), daß die
Prüfbaugruppen, -bausteine und B1, B2 parallel an die Haupt-
taktleitungen angeschlossen sind. Die Hauptleitungen TÜ1-a
TÜ2 enden jeweils an einem Ausgangsspeicher (AS1 und AS2) für
den Geheimtext. Der Ausfall des Taktes TÜ1 oder TÜ2
auf der Hauptleitung entspricht damit einer Blockierung
des Geheimtextausgangs der Chiffriereinrichtung.
Durch das Signal B0 kann die Blockierung der Chiffrierein-
richtung aufgehoben werden. (s. Kap. III, §1, Punkt 3)
B1 und B2 sind parallel an die Leitung B0 angeschlossen.
Diese Leitung endet an den Schaltern S2 und S4. Wenn das Sig-
nal B0 aufgrund von Fehlern ständig in der Chiffriereinrich-
tung vorhanden ist, führt es zwar einerseits zur Wirkungslo-
sigkeit der meisten Prüfungen, aber andererseits zugleich
auch zur Blockierung des Geheimtextausganges.
Kryptologisch wesentliche Prüfungen und Blockierungen sind
damit doppelt ausgeführt. Das gilt für den Vergleich der
von FG1 und FG2 erzeugten F-Folgen (Dopplung des Vergleiches
in P-F), für die Prüfung FUi ≡ constant (P-FU parallel zu
P-FU-P), für die Prüfung Wi ≡ constant. (P-W-P parallel zu P-W),
für den Vergleich der Ausgänge A1 und A2 (Dopplung des
Vergleichs in P-2 ⊕ KT2), für die Blockierung des Ausganges
für den Geheimtext (B1 und S3 parallel zu B2 und S4).
Zur Kontrolle der Prüfbaugruppen, -bausteine, der Bau-
gruppen B1, B2 und von S3, S4 können durch Drücken verschie-
dener Prüftasten in der Chiffriereinrichtung die einzelnen
Fehler erzeugt werden, auf die die Prüfung und die
Blockierung ansprechen müssen bei fehlerfreier Arbeit -
"Handprüfung".
Der Zeitraum ∆t für diese Handprüfung ist für den Einsatz
der serienmäßig produzierten Anlage OPERATION so zu
bestimmen, daß die Wahrscheinlichkeit dafür, daß die
Blockierung des Geheimtextausganges der Chiffriereinrichtung
zum Zeitpunkt t2 nicht ausgelöst wird, wenn zum Zeitpunkt
t1 (t2-t1 ≤ ∆t) die Chiffriereinrichtung fehlerfrei
gearbeitet hat, und wenn zum Zeitpunkt t2 ein Fehler in einer
Baueinheit der Chiffriereinrichtung auftritt, der bei
richtiger Funktion der Prüfungen und Blockierungen zur
Blockierung des Geheimtextausganges der Chiffriereinrichtung
führen würde, ausreichend klein ist.
§3 Bedienungsfehler und deren Einfluß auf die
kryptologische Sicherheit
1. Mehrmalige Verwendung des gleichen Kurzzeitschlüssels S
Die mehrmalige Verwendung des gleichen Kurzzeitschlüssels S
ist äquivalent der Verlängerung der Gültigkeit von S.
Als Folge dieses Fehlers steht dem Dekrypteur eine
größere Menge von Ausgangsmaterial (mehr Geheimtexte,
eventuell mehr Zuordnungen F-Abschnitt-Additionsreihe)
zur Dekryptierung zur Verfügung.
Die mehrmalige Verwendung des gleichen Schlüssels S ist
jedoch auf dem Übertragungskanal nicht erkennbar.
Beim Wechsel des Kurzzeitschlüssels S wird die Erzeugung
der Folge F nicht unterbrochen. Sollte die Erzeugung von F
jedoch aus irgendwelchen Gründen unterbrochen werden, so
wird nach der Unterbrechung, sofern keine technischen
Fehler auftreten, automatisch wieder ein zufälliger
Anfangswert für die weitere Erzeugung von F gebildet.
Wenn durch die mehrmalige Verwendung des gleichen
Schlüssels S dessen Gültigkeit praktisch auf eine Woche
verlängert wird, so ist die Wahrscheinlichkeit dafür, daß
während der Gültigkeitsdauer dieses Schlüssels gleiche
F-Folgenabschnitte erzeugt werden, kleiner als 10-6.
2. Verwendung fehlerhafter Kurzzeitschlüssel S
Unter den schlüsseln der theoretisch möglichen Schlüssel-
menge
erfüllt ist. Diese Bedingung ist nicht erfüllt, wenn S1
oder S2 identisch 0 oder identisch 1 ist.
Unter der Voraussetzung, daß bei S1 const. oder S2 const.
in P-S1/S2 die Blockierung ausgelöst wird (M4-SE = 1),
entstehen nicht erkennbare Fehler oben erwähnter Art nur dann, wenn zu-
gleich oder nahezu zugleich (Zeiteinheit ∆t) die Verbindung
Verzweigungspunkt G oder/und H Chiffrator und die Verbindung
Verzweigungspunkt G oder/und H Prüf-Chiffrator unterbrochen
werden. Die Wahrscheinlichkeit solcher gleichzeitig oder nahe-
zu gleichzeitig (Zeiteinheit ∆t) auftretender Fehler ist
sehr gering.
6. Technische Fehler in den Prüfbaugruppen, -bausteinen
und Baugruppen B1, B2
Kryptologisch sind nur die technischen Fehler von Bedeu-
tung, die selbst nicht zur Blockierung führen und es über
dies zulassen, daß bei auftretenden Fehlern in den anderen
Baugruppen keine Blockierung der Chiffriereinrichtung aus-
gelöst wird.
Fehler dieser Art sind im normalen Betrieb der Anlage nicht
sofort erkennbar. Sie können sich bemerkbar machen durch
Ausfall des gesamten Systems, wenn zusätzlich ein entsprechen-
der Fehler bei der Bildung des Geheimtextes auftritt (alle
Stationen E können die empfangenen Nachrichten nicht mehr
dechiffrieren).
Die Prüfbausteine (außer P-t104) bestehen nur aus wenigen
Bauelementen (maximal 3 Schaltkreise vom Typ KME-10).
Für die Funktionsfähigkeit der Prüfbaugruppen, -bausteine
und von B1, B2 ist ihre Taktung mit dem Übertragungstakt TÜ
(Abfrage des Prüfergebnisses) notwendig (außer P-F und
P-W ⊕ KT2).
Die Taktführung ist so gestaltet (TÜ1 und TÜ2), daß die
Prüfbaugruppen, -bausteine und B1, B2 parallel an die Haupt-
taktleitungen angeschlossen sind. Die Hauptleitungen TÜ1-a
TÜ2 enden jeweils an einem Ausgangsspeicher (AS1 und AS2) für
den Geheimtext. Der Ausfall des Taktes TÜ1 oder TÜ2
auf der Hauptleitung entspricht damit einer Blockierung
des Geheimtextausgangs der Chiffriereinrichtung.
Durch das Signal B0 kann die Blockierung der Chiffrierein-
richtung aufgehoben werden. (s. Kap. III, §1, Punkt 3)
B1 und B2 sind parallel an die Leitung B0 angeschlossen.
Diese Leitung endet an den Schaltern S2 und S4. Wenn das Sig-
nal B0 aufgrund von Fehlern ständig in der Chiffriereinrich-
tung vorhanden ist, führt es zwar einerseits zur Wirkungslo-
sigkeit der meisten Prüfungen, aber andererseits zugleich
auch zur Blockierung des Geheimtextausganges.
Kryptologisch wesentliche Prüfungen und Blockierungen sind
damit doppelt ausgeführt. Das gilt für den Vergleich der
von FG1 und FG2 erzeugten F-Folgen (Dopplung des Vergleiches
in P-F), für die Prüfung FUi ≡ constant (P-FU parallel zu
P-FU-P), für die Prüfung Wi ≡ constant. (P-W-P parallel zu P-W),
für den Vergleich der Ausgänge A1 und A2 (Dopplung des
Vergleichs in P-2 ⊕ KT2), für die Blockierung des Ausganges
für den Geheimtext (B1 und S3 parallel zu B2 und S4).
Zur Kontrolle der Prüfbaugruppen, -bausteine, der Bau-
gruppen B1, B2 und von S3, S4 können durch Drücken verschie-
dener Prüftasten in der Chiffriereinrichtung die einzelnen
Fehler erzeugt werden, auf die die Prüfung und die
Blockierung ansprechen müssen bei fehlerfreier Arbeit -
"Handprüfung".
Der Zeitraum ∆t für diese Handprüfung ist für den Einsatz
der serienmäßig produzierten Anlage OPERATION so zu
bestimmen, daß die Wahrscheinlichkeit dafür, daß die
Blockierung des Geheimtextausganges der Chiffriereinrichtung
zum Zeitpunkt t2 nicht ausgelöst wird, wenn zum Zeitpunkt
t1 (t2-t1 ≤ ∆t) die Chiffriereinrichtung fehlerfrei
gearbeitet hat, und wenn zum Zeitpunkt t2 ein Fehler in einer
Baueinheit der Chiffriereinrichtung auftritt, der bei
richtiger Funktion der Prüfungen und Blockierungen zur
Blockierung des Geheimtextausganges der Chiffriereinrichtung
führen würde, ausreichend klein ist.
§3 Bedienungsfehler und deren Einfluß auf die
kryptologische Sicherheit
1. Mehrmalige Verwendung des gleichen Kurzzeitschlüssels S
Die mehrmalige Verwendung des gleichen Kurzzeitschlüssels S
ist äquivalent der Verlängerung der Gültigkeit von S.
Als Folge dieses Fehlers steht dem Dekrypteur eine
größere Menge von Ausgangsmaterial (mehr Geheimtexte,
eventuell mehr Zuordnungen F-Abschnitt-Additionsreihe)
zur Dekryptierung zur Verfügung.
Die mehrmalige Verwendung des gleichen Schlüssels S ist
jedoch auf dem Übertragungskanal nicht erkennbar.
Beim Wechsel des Kurzzeitschlüssels S wird die Erzeugung
der Folge F nicht unterbrochen. Sollte die Erzeugung von F
jedoch aus irgendwelchen Gründen unterbrochen werden, so
wird nach der Unterbrechung, sofern keine technischen
Fehler auftreten, automatisch wieder ein zufälliger
Anfangswert für die weitere Erzeugung von F gebildet.
Wenn durch die mehrmalige Verwendung des gleichen
Schlüssels S dessen Gültigkeit praktisch auf eine Woche
verlängert wird, so ist die Wahrscheinlichkeit dafür, daß
während der Gültigkeitsdauer dieses Schlüssels gleiche
F-Folgenabschnitte erzeugt werden, kleiner als 10-6.
2. Verwendung fehlerhafter Kurzzeitschlüssel S
Unter den schlüsseln der theoretisch möglichen Schlüssel-
menge  gibt es keine kryptologisch schlechten Schlüssel.
Die Verwendung fehlerhafter Schlüssel ist auf dem Übertra-
gungskanal nicht erkennbar. Außer den schlüsseln S = (S1,S2)
mit S1 oder S2 identisch 0 oder identisch 1 sind unter
den Schlüssel von
gibt es keine kryptologisch schlechten Schlüssel.
Die Verwendung fehlerhafter Schlüssel ist auf dem Übertra-
gungskanal nicht erkennbar. Außer den schlüsseln S = (S1,S2)
mit S1 oder S2 identisch 0 oder identisch 1 sind unter
den Schlüssel von  keine weiteren Schlüssel bekannt, die
infolge von Fehlern, seien es technische Fehler oder
Bedienungsfehler, mit größerer Wahrscheinlichkeit Verwendung
finden könnten.
Die Verwendung fehlerhafter Kurzzeitschlüssel hat damit
kryptologisch keine Auswirkungen.
Diese Situation ändert sich, wenn zur Prüfung der Funktions-
einheiten der Chiffriereinrichtung mit einem speziellen
Prüfkurzzeitschlüssel gearbeitet wird. Es ist denkbar, daß
unter gewissen Umständen dieser Prüfkurzzeitschlüssel
auch fehlerhaft als Kurzzeitschlüssel im normalen Betrieb
der Anlage eingesetzt wird.
Diese Möglichkeit besteht z. B. dann, wenn nach einer
Prüfung beim Übergang zum normalen Betrieb der Prüfkurz-
zeitschlüssel nicht automatisch gelöscht wird.
Zur Arbeit mit einem Prüfkurzzeitschlüssel sind noch
keine Festlegungen getroffen worden.
Bei der Festlegung der Prüfvorschrift muß diese
Möglichkeit beachtet werden.
3. Sonstige Bedienungsfehler
Außer der fehlerhaften Verwendung des Prüfkurzzeitschlüssels
wurde bisher keine reale Möglichkeit für Fehler bei der
Bedienung und Wartung der Chiffriereinrichtung mit krypto-
logischen Auswirkungen festgestellt.
Das gilt auch für Fehler bei der Bedingung und Wartung der
gesamten Anlage. Aufgrund der hohen Automatisierung der
Anlage sind eine Reihe subjektiver Fehler ausgeschlossen,
die bei anderen Chiffrierverfahren möglich sind (z. B. Über-
mittlung von Klartext, mehrmalige Benutzung der gleichen
Kenngruppe).
Ein Mangel des Chiffrierverfahrens im System OPERATION
ist die Notwendigkeit zur Übermittlung von Blendnachrichten
(s. Kap. I, §2, Punkt 5.). Die Blendnachrichten werden nicht
automatisch ausgelöst. Wenn Blendnachrichten nicht in ent-
sprechender Häufigkeit, speziell, wenn zu wenig Blendnach-
richten ausgelöst werden, können durch den Dekrypteur aus
den Zeitpunkten der Übermittlung von Nachrichten gewisse
Rückschlüsse auf deren Inhalt gemacht werden.
Zusammenfassung
1. Zusammenfassung der Resultate des Kapitels IV
Im Kapitel IV wird die Struktur der Chiffrierabbildung
ausgehend von der Grundvoraussetzung, daß der Prozeß der
Umformung des Inhalts des Registers U entscheidend ist,
untersucht. Wenn er gut ist, so kann man eine Methode der
Erzeugung einer guten Additionsreihe finden. Der Prozeß
ist gut, wenn insbesondere gilt:
- es gibt keine unwesentlichen Zustände (im Sinne der
Theorie Markowscher Ketten),
- alle Zustände bilden eine Klasse,
- alle Zustände sind asymptomatisch gleichwahrscheinlich,
- die Periodizität ist maximal,
- die Abhängigkeit von den Eingangselementen ist wesentlich
und kompliziert,
- es sind solche mathematischen Eigenschaften vorhanden, die
es nicht gestatten, Dekrypteur-Methoden anzuwenden, die
wesentlich effektiver sind als die totale Probiermethode,
insbesondere analytische Methoden.
Im Laufe der Untersuchungen wurden in dieser Richtung
folgende Hauptresultate erhalten:
(1) Es existiert eine Klasse PR von Elementen (P,R)
des Langzeitschlüssels, die mehr als 1026 Elemente
enthält, bei deren Anwendung keine unwesentlichen Zu-
stände auftreten.
(2) Die Zustandsklassen enthalten mindestens 512 Elemente,
es gibt nicht mehr als 218 Klassen.
Im Spezialfall (P0,R0) gibt es nicht mehr als 215
Klassen, jede mit 4096 Elementen oder mehr; experimen-
tell wurde festgestellt, daß eine der Klassen nicht
weniger als 27,7*106 Elemente enthält.
(3) Unter gewissen Voraussetzungen sind alle Zustände asymp-
totisch gleichwahrscheinlich. Es wurden starke Argumente
dafür gewonnen, daß man annehmen kann, daß die
Additionsreihen gute statistische Eigenschaften besitzen.
(4) Es wurde eine Abschätzung für die Periode P der Umfor-
mung des Inhalts des Registers U gefunden:
104 * (252-1) ≤ P ≤ 227*104(252-1).
(5) Es gibt keine äquivalenten schlüssel bezüglich der
Folge der Inhalte des Registers U.
(6) Es gibt keine äquivalenten Schlüssel bezüglich der
Folge der ersten Elemente der Inhalte des Registers U
für alle Anfangszustände des U - Registers gleichzeitig.
(7) Es wurde ein stochastisches Modell des Chiffrators
gefunden, da sich nicht wesentlich von der tatsäch-
lichen Chiffrierabbildung unterscheidet, in dem die
Additionsreihen zufällige gleichwahrscheinliche
Folgen sind.
Wichtige, bis jetzt nicht gelöste Probleme (bezüglich der
Thematik Kapitel IV) sind:
(1) Die Zahl und die Mächtigkeit der Zustandsklassen; für
welche (P,R) bilden alle Zustände eine Klasse?
(2) Die analytische Abhängigkeit der Elemente der Additions-
reihe von Anfangswerten.
(3) Die Periode der Additionsreihe
(4) Eine Abschätzung der Mächtigkeit der Klassen äquivalen-
ter Schlüssel bezüglich der Additionsreihe; gibt es
äquivalente Schlüssel bezüglich der Additionsreihe?
(5) Eine tiefere theoretische Untersuchung der statistischen
Eigenschaften der Additionsreihe.
(6) Eine experimentelle Untersuchung der statistischen
Eigenschaften der Additionsreihen auf EDVA.
2. Zusammenfassung der Resultate des Kapitels V
Das Studium einige Methoden der Dekryptierung zeigt, daß
die Chiffrierabbildung sogar bei Vorhandensein großer Klas-
sen äquivalenter Schlüssel sicher bleibt. Nach den Resulta-
ten im Kapitel IV existieren solche (großen) Klassen nicht.
Es wurde die Aufgabe der Bestimmung des Schlüssels unter der
Voraussetzung, daß Komponentenfolgen bekannt sind, untersucht.
Es wurden Bedingungen gefunden, unter denen diese Aufgabe
lösbar ist.
Es wird ein Verzeichnis der möglichen technischen Fehler im
System und insbesondere in der Chiffriervorrichtung, die die
kryptologische Sicherheit herabsetzen könnten, angegeben.
Daraus wird der Schluß gezogen, daß entweder das System des
Schutzes vor Fehlern anspricht oder daß der Fehler äußerst
unwahrscheinlich ist.
Es werden möglich Fehler bei der Bedienung betrachtet, und
analoge Resultate abgeleitet.
Offen blieben vor allem folgenden Probleme:
- Das Finden einer Methode zur Bestimmung des Schlüssels mit
minimaler Anzahl von Elementaroperationen;
- Eine Methode des Lesens des Textes ohne Bestimmung des
Schlüssels;
- Eine detaillierte Untersuchung der Folgen gewisser Fehler.
3. Das Schlüsselsystem und kryptologische Reserven
3.1 Es wird empfohlen, den Schlüsselwechsel ein- oder zweimal
täglich durchzuführen.
3.2 Kriterien für die Auswahl der Elemente des Langzeitschlüssels:
Die Elemente (P,R)
Zu empfehlen ist (P,R) ∈ PR.
Die Mehrheit der Resultate wurde unter dieser Voraussetzung
erhalten, wobei diese ziemlich oft wesentlich war.
Für die Muster des Chiffrators empfehlen wir (P,R) = (P0,R0).
Das Element U0 (die Anfangsbelegung des
keine weiteren Schlüssel bekannt, die
infolge von Fehlern, seien es technische Fehler oder
Bedienungsfehler, mit größerer Wahrscheinlichkeit Verwendung
finden könnten.
Die Verwendung fehlerhafter Kurzzeitschlüssel hat damit
kryptologisch keine Auswirkungen.
Diese Situation ändert sich, wenn zur Prüfung der Funktions-
einheiten der Chiffriereinrichtung mit einem speziellen
Prüfkurzzeitschlüssel gearbeitet wird. Es ist denkbar, daß
unter gewissen Umständen dieser Prüfkurzzeitschlüssel
auch fehlerhaft als Kurzzeitschlüssel im normalen Betrieb
der Anlage eingesetzt wird.
Diese Möglichkeit besteht z. B. dann, wenn nach einer
Prüfung beim Übergang zum normalen Betrieb der Prüfkurz-
zeitschlüssel nicht automatisch gelöscht wird.
Zur Arbeit mit einem Prüfkurzzeitschlüssel sind noch
keine Festlegungen getroffen worden.
Bei der Festlegung der Prüfvorschrift muß diese
Möglichkeit beachtet werden.
3. Sonstige Bedienungsfehler
Außer der fehlerhaften Verwendung des Prüfkurzzeitschlüssels
wurde bisher keine reale Möglichkeit für Fehler bei der
Bedienung und Wartung der Chiffriereinrichtung mit krypto-
logischen Auswirkungen festgestellt.
Das gilt auch für Fehler bei der Bedingung und Wartung der
gesamten Anlage. Aufgrund der hohen Automatisierung der
Anlage sind eine Reihe subjektiver Fehler ausgeschlossen,
die bei anderen Chiffrierverfahren möglich sind (z. B. Über-
mittlung von Klartext, mehrmalige Benutzung der gleichen
Kenngruppe).
Ein Mangel des Chiffrierverfahrens im System OPERATION
ist die Notwendigkeit zur Übermittlung von Blendnachrichten
(s. Kap. I, §2, Punkt 5.). Die Blendnachrichten werden nicht
automatisch ausgelöst. Wenn Blendnachrichten nicht in ent-
sprechender Häufigkeit, speziell, wenn zu wenig Blendnach-
richten ausgelöst werden, können durch den Dekrypteur aus
den Zeitpunkten der Übermittlung von Nachrichten gewisse
Rückschlüsse auf deren Inhalt gemacht werden.
Zusammenfassung
1. Zusammenfassung der Resultate des Kapitels IV
Im Kapitel IV wird die Struktur der Chiffrierabbildung
ausgehend von der Grundvoraussetzung, daß der Prozeß der
Umformung des Inhalts des Registers U entscheidend ist,
untersucht. Wenn er gut ist, so kann man eine Methode der
Erzeugung einer guten Additionsreihe finden. Der Prozeß
ist gut, wenn insbesondere gilt:
- es gibt keine unwesentlichen Zustände (im Sinne der
Theorie Markowscher Ketten),
- alle Zustände bilden eine Klasse,
- alle Zustände sind asymptomatisch gleichwahrscheinlich,
- die Periodizität ist maximal,
- die Abhängigkeit von den Eingangselementen ist wesentlich
und kompliziert,
- es sind solche mathematischen Eigenschaften vorhanden, die
es nicht gestatten, Dekrypteur-Methoden anzuwenden, die
wesentlich effektiver sind als die totale Probiermethode,
insbesondere analytische Methoden.
Im Laufe der Untersuchungen wurden in dieser Richtung
folgende Hauptresultate erhalten:
(1) Es existiert eine Klasse PR von Elementen (P,R)
des Langzeitschlüssels, die mehr als 1026 Elemente
enthält, bei deren Anwendung keine unwesentlichen Zu-
stände auftreten.
(2) Die Zustandsklassen enthalten mindestens 512 Elemente,
es gibt nicht mehr als 218 Klassen.
Im Spezialfall (P0,R0) gibt es nicht mehr als 215
Klassen, jede mit 4096 Elementen oder mehr; experimen-
tell wurde festgestellt, daß eine der Klassen nicht
weniger als 27,7*106 Elemente enthält.
(3) Unter gewissen Voraussetzungen sind alle Zustände asymp-
totisch gleichwahrscheinlich. Es wurden starke Argumente
dafür gewonnen, daß man annehmen kann, daß die
Additionsreihen gute statistische Eigenschaften besitzen.
(4) Es wurde eine Abschätzung für die Periode P der Umfor-
mung des Inhalts des Registers U gefunden:
104 * (252-1) ≤ P ≤ 227*104(252-1).
(5) Es gibt keine äquivalenten schlüssel bezüglich der
Folge der Inhalte des Registers U.
(6) Es gibt keine äquivalenten Schlüssel bezüglich der
Folge der ersten Elemente der Inhalte des Registers U
für alle Anfangszustände des U - Registers gleichzeitig.
(7) Es wurde ein stochastisches Modell des Chiffrators
gefunden, da sich nicht wesentlich von der tatsäch-
lichen Chiffrierabbildung unterscheidet, in dem die
Additionsreihen zufällige gleichwahrscheinliche
Folgen sind.
Wichtige, bis jetzt nicht gelöste Probleme (bezüglich der
Thematik Kapitel IV) sind:
(1) Die Zahl und die Mächtigkeit der Zustandsklassen; für
welche (P,R) bilden alle Zustände eine Klasse?
(2) Die analytische Abhängigkeit der Elemente der Additions-
reihe von Anfangswerten.
(3) Die Periode der Additionsreihe
(4) Eine Abschätzung der Mächtigkeit der Klassen äquivalen-
ter Schlüssel bezüglich der Additionsreihe; gibt es
äquivalente Schlüssel bezüglich der Additionsreihe?
(5) Eine tiefere theoretische Untersuchung der statistischen
Eigenschaften der Additionsreihe.
(6) Eine experimentelle Untersuchung der statistischen
Eigenschaften der Additionsreihen auf EDVA.
2. Zusammenfassung der Resultate des Kapitels V
Das Studium einige Methoden der Dekryptierung zeigt, daß
die Chiffrierabbildung sogar bei Vorhandensein großer Klas-
sen äquivalenter Schlüssel sicher bleibt. Nach den Resulta-
ten im Kapitel IV existieren solche (großen) Klassen nicht.
Es wurde die Aufgabe der Bestimmung des Schlüssels unter der
Voraussetzung, daß Komponentenfolgen bekannt sind, untersucht.
Es wurden Bedingungen gefunden, unter denen diese Aufgabe
lösbar ist.
Es wird ein Verzeichnis der möglichen technischen Fehler im
System und insbesondere in der Chiffriervorrichtung, die die
kryptologische Sicherheit herabsetzen könnten, angegeben.
Daraus wird der Schluß gezogen, daß entweder das System des
Schutzes vor Fehlern anspricht oder daß der Fehler äußerst
unwahrscheinlich ist.
Es werden möglich Fehler bei der Bedienung betrachtet, und
analoge Resultate abgeleitet.
Offen blieben vor allem folgenden Probleme:
- Das Finden einer Methode zur Bestimmung des Schlüssels mit
minimaler Anzahl von Elementaroperationen;
- Eine Methode des Lesens des Textes ohne Bestimmung des
Schlüssels;
- Eine detaillierte Untersuchung der Folgen gewisser Fehler.
3. Das Schlüsselsystem und kryptologische Reserven
3.1 Es wird empfohlen, den Schlüsselwechsel ein- oder zweimal
täglich durchzuführen.
3.2 Kriterien für die Auswahl der Elemente des Langzeitschlüssels:
Die Elemente (P,R)
Zu empfehlen ist (P,R) ∈ PR.
Die Mehrheit der Resultate wurde unter dieser Voraussetzung
erhalten, wobei diese ziemlich oft wesentlich war.
Für die Muster des Chiffrators empfehlen wir (P,R) = (P0,R0).
Das Element U0 (die Anfangsbelegung des  -Registers)
Es wird empfohlen, U0 aus einer Klasse von Zuständen zu neh-
men, die einen Fixpunkt enthalten, und die soviel wie möglich
Elemente besitzen.
Für die Muster des Chiffrators wird
U0 = (u
-Registers)
Es wird empfohlen, U0 aus einer Klasse von Zuständen zu neh-
men, die einen Fixpunkt enthalten, und die soviel wie möglich
Elemente besitzen.
Für die Muster des Chiffrators wird
U0 = (u ,u
,u , …, u
, …, u ) = (000 000 011 011 111 111 111 100 000 000)
empfohlen. Dieser Wert U0 ∈ {ϕU*}, wobei U* einer der Fix-
punkte der Klasse ist, die auf einer EDVA berechnet wurden,
Siehe Kapitel IV, §1, 3.1 und 5.5.
Das Element α (Die Abgriffstelle der Additionsreihe)
Es wird empfohlen α = 1.
Bei der Untersuchung hatte die konkrete Wahl von α nur
in Zusammenhang mit äquivalenten Schlüsseln eine Bedeutung,
aber in diesem Fall erwies sich die Wahl von α = 1 als
die beste.
Außerdem kann die erste Stelle der Additionsreihe nur bei
α = 1 von allen Schlüsselelementen abhängen.
3.3 Die kryptologische Schaltung, die im Kapitel III (siehe
Abb. 3.1) beschrieben und technisch realisiert wurde, ver-
allgemeinert die im Kapitel IV und V untersuchte Chiffrier-
abbildung in dem Sinne, daß diese Chiffrierabbildung bei
spezieller Wahl der Elemente U0, P und Q = R-1 realisiert wird.
Deshalb kann man beim Finden von Schwächen der Chiffrierab-
bildung auf die verallgemeinerte kryptologische Schaltung
übergehen.
Eine weitere mächtige Reserve stellen die in Kapitel III auf-
gezeigte Veränderung der kryptologischen Schaltung dar, die
man bis zum Beginn der Serienproduktion des Chiffrators aus-
nutzen kann:
- die Abänderung der Struktur des U-Registers,
- die Veränderung der logischen Funktion Z,
- der Anfangswert U0 des
) = (000 000 011 011 111 111 111 100 000 000)
empfohlen. Dieser Wert U0 ∈ {ϕU*}, wobei U* einer der Fix-
punkte der Klasse ist, die auf einer EDVA berechnet wurden,
Siehe Kapitel IV, §1, 3.1 und 5.5.
Das Element α (Die Abgriffstelle der Additionsreihe)
Es wird empfohlen α = 1.
Bei der Untersuchung hatte die konkrete Wahl von α nur
in Zusammenhang mit äquivalenten Schlüsseln eine Bedeutung,
aber in diesem Fall erwies sich die Wahl von α = 1 als
die beste.
Außerdem kann die erste Stelle der Additionsreihe nur bei
α = 1 von allen Schlüsselelementen abhängen.
3.3 Die kryptologische Schaltung, die im Kapitel III (siehe
Abb. 3.1) beschrieben und technisch realisiert wurde, ver-
allgemeinert die im Kapitel IV und V untersuchte Chiffrier-
abbildung in dem Sinne, daß diese Chiffrierabbildung bei
spezieller Wahl der Elemente U0, P und Q = R-1 realisiert wird.
Deshalb kann man beim Finden von Schwächen der Chiffrierab-
bildung auf die verallgemeinerte kryptologische Schaltung
übergehen.
Eine weitere mächtige Reserve stellen die in Kapitel III auf-
gezeigte Veränderung der kryptologischen Schaltung dar, die
man bis zum Beginn der Serienproduktion des Chiffrators aus-
nutzen kann:
- die Abänderung der Struktur des U-Registers,
- die Veränderung der logischen Funktion Z,
- der Anfangswert U0 des  -Registers hängt vom
(Kurzzeit-) Schlüssel S ab.
4. Richtung der weiteren Untersuchungen der kryptologischen
Schaltung
4.1 Die wichtigste Richtung besteht in Methoden der Dekryptierung
und damit verbundenen Fragen.
Insbesondere muß man den Fall der im gewissen Sinne "nahen"
Additionsreihe sowie die analytischen Dekryptierungen unter-
suchen.
Im Zusammenhang damit muß man die Kriterien der Auswahl des
Langzeitschlüssels präzisieren.
4.2 Bezüglich der Struktur des Chiffrators:
- die Äquivalenz der Schlüssel bezüglich der Additionsreihe,
- Suche nach Methoden der Abschätzung der Anzahl der Zustands-
klassen,
- Untersuchung der angenäherten (im Sinne von Kapitel IV,
§2) kryptologischen Schaltung.
4.3 Bezüglich der Arbeit mit er EDVA:
- Fortsetzung der Berechnung der Zustandsklassen (Kapitel
IV, §1, 5.).
- Untersuchung der statistischen Eigenschaften der Additions-
reihen (Kapitel IV, §4, 3.),
- Rechnen mit logischen Funktionen (Kapitel IV, §2, 4.).
4.4 Weitere Untersuchungen über das System des Schutzes vor
technischen Fehlern und Fehlern in der Bedingung des Systems
OPERATION.
Schlußfolgerungen
1. Unter den Voraussetzungen, daß
- die kryptologische Schaltung, die Gebrauchsanweisung,
das Schlüsselsystem und die Langzeitschlüssel bekannt
sind;
- der Langzeitschlüssel nach den im Punkt 3. der Zusammen-
fassung angegebenen Kriterien gewählt wird;
- im Chiffrator keine technischen Fehler auftreten;
- kein Verstoß gegen die Gebrauchsanweisung des Chiffrators
zugelassen wird,
beträgt die kryptologische Sicherheit des Chiffrators nicht
weniger als 1025 Elementaroperationen, was bei einer Geschwin-
digkeit von 1011 Elementaroperationen/sec. nicht weniger als
107 Jahre Rechenzeit auf der EDVA bedeutet.
2. Das System des Schutzes vor technischen Fehlern ist hinrei-
chend vollständig und zuverlässig. Insbesondere spricht es
bei Fehlern in der Bedienung an. Somit verringert sich bei
technischen Fehlern und bei Fehlern in der Bedienung die
kryptologische Sicherheit des Chiffrators in der Praxis nicht.
3. Der Chiffrator des Systems OPERATION genügt den gestellten
Forderungen an die Sicherheit der Chiffrierung und kann im
System OPERATION angewandt werden.
Krey Helbig
Hauptmann Oberleutnant
einverstanden: Leiter der Unterabteilung
Hübler
Major
ЛИTEPATУPA / Literatur
/1/ Technisch-taktische-Forderungen für die Entwicklung einer technischen
Einrichtung zur Nachrichtenübermittlung und Anzeige (Deckbezeichnung
SKS V/1), VVS B 100/L/1/71
/2/ OБЩИE OПEPATИBHЫE TPEБOBAHИЯ K ПAPAMETPAM ШИФPУЮЩEГO
УCTOЙCTBA AППAPATУPЫ "OПEPAЦИЯ"
(ПИЬCMO K-72 OT 2-ГO ИЮHЯ I973 Г. AППAPATA ПO KOOPДИHAЦИИ
B BAPШABE)
/3/ ПOДCИCTEMA ЗAШИФPOBAHИE/PACШИФPOBAHИE B CИCTEME OПEPAЦИЯ,
COB. CEK. № 020-638/72
/4/ ПPEДBAPИTEЛЬHOE ЗAKЛЮЧEHИE o KPИПTOГPAФИЧECKOЙ CTOЙKOCTИ
ШИФPATOPA CИCTEMЫ
-Registers hängt vom
(Kurzzeit-) Schlüssel S ab.
4. Richtung der weiteren Untersuchungen der kryptologischen
Schaltung
4.1 Die wichtigste Richtung besteht in Methoden der Dekryptierung
und damit verbundenen Fragen.
Insbesondere muß man den Fall der im gewissen Sinne "nahen"
Additionsreihe sowie die analytischen Dekryptierungen unter-
suchen.
Im Zusammenhang damit muß man die Kriterien der Auswahl des
Langzeitschlüssels präzisieren.
4.2 Bezüglich der Struktur des Chiffrators:
- die Äquivalenz der Schlüssel bezüglich der Additionsreihe,
- Suche nach Methoden der Abschätzung der Anzahl der Zustands-
klassen,
- Untersuchung der angenäherten (im Sinne von Kapitel IV,
§2) kryptologischen Schaltung.
4.3 Bezüglich der Arbeit mit er EDVA:
- Fortsetzung der Berechnung der Zustandsklassen (Kapitel
IV, §1, 5.).
- Untersuchung der statistischen Eigenschaften der Additions-
reihen (Kapitel IV, §4, 3.),
- Rechnen mit logischen Funktionen (Kapitel IV, §2, 4.).
4.4 Weitere Untersuchungen über das System des Schutzes vor
technischen Fehlern und Fehlern in der Bedingung des Systems
OPERATION.
Schlußfolgerungen
1. Unter den Voraussetzungen, daß
- die kryptologische Schaltung, die Gebrauchsanweisung,
das Schlüsselsystem und die Langzeitschlüssel bekannt
sind;
- der Langzeitschlüssel nach den im Punkt 3. der Zusammen-
fassung angegebenen Kriterien gewählt wird;
- im Chiffrator keine technischen Fehler auftreten;
- kein Verstoß gegen die Gebrauchsanweisung des Chiffrators
zugelassen wird,
beträgt die kryptologische Sicherheit des Chiffrators nicht
weniger als 1025 Elementaroperationen, was bei einer Geschwin-
digkeit von 1011 Elementaroperationen/sec. nicht weniger als
107 Jahre Rechenzeit auf der EDVA bedeutet.
2. Das System des Schutzes vor technischen Fehlern ist hinrei-
chend vollständig und zuverlässig. Insbesondere spricht es
bei Fehlern in der Bedienung an. Somit verringert sich bei
technischen Fehlern und bei Fehlern in der Bedienung die
kryptologische Sicherheit des Chiffrators in der Praxis nicht.
3. Der Chiffrator des Systems OPERATION genügt den gestellten
Forderungen an die Sicherheit der Chiffrierung und kann im
System OPERATION angewandt werden.
Krey Helbig
Hauptmann Oberleutnant
einverstanden: Leiter der Unterabteilung
Hübler
Major
ЛИTEPATУPA / Literatur
/1/ Technisch-taktische-Forderungen für die Entwicklung einer technischen
Einrichtung zur Nachrichtenübermittlung und Anzeige (Deckbezeichnung
SKS V/1), VVS B 100/L/1/71
/2/ OБЩИE OПEPATИBHЫE TPEБOBAHИЯ K ПAPAMETPAM ШИФPУЮЩEГO
УCTOЙCTBA AППAPATУPЫ "OПEPAЦИЯ"
(ПИЬCMO K-72 OT 2-ГO ИЮHЯ I973 Г. AППAPATA ПO KOOPДИHAЦИИ
B BAPШABE)
/3/ ПOДCИCTEMA ЗAШИФPOBAHИE/PACШИФPOBAHИE B CИCTEME OПEPAЦИЯ,
COB. CEK. № 020-638/72
/4/ ПPEДBAPИTEЛЬHOE ЗAKЛЮЧEHИE o KPИПTOГPAФИЧECKOЙ CTOЙKOCTИ
ШИФPATOPA CИCTEMЫ OПEPAЦИЯ
, COB. CEK. № Л-I860
/5/ AЛГOPИФM ДЛЯ BЫPAБOTKИ ГAMMЫ HAЛOЖEHИЯ
GVS MfS 020 Nr. 290/73
/6/ HEKOTOPЫE CBOЙCTBA KPИПTOCХEMЫ ШИФPATOPA CИCTEMЫ OПEPAЦИЯ
GVS MfS 020 Nr. XI/440/73
/7/ AF 3 - Bericht SKS V/1, VVS B 198 - 35/73
/8/ Pflichtenheft SKS V/1, Entwurf, VVS B 198 - 45/73
COBEPШEHHO CEKPETHO!
Geheime Verschlußsache
MfS 020 Nr. XI/76/74
……..Ausfertigungen
05. Ausfertigung 41 Blatt
Kryptologische Analyse des Chiffrators
des Systems OPERATION
- Erste Ergänzung -
Bestätigt: Leiter des Zentralen Chiffrierorgans
im Ministerium für Staatssicherheit
der Deutschen Demokratischen Republik
Schürrmann
Oberst
Inhalt:
1. Einleitung
2. Darlegung zu den Kapiteln I - III
2.1. Bausteintechnik
2.2. Schema der Chiffrierverbindungen
2.3. Kryptologische Schaltung
2.4. Nachrichten
3. Darlegungen zu Kapitel IV
3.1. Zerlegung der Abbildung ϕ(0,0,0) in Zyklen
3.2. Korrektur zu [1; IV, §2, 1.]
3.3. Die logische Funktion h 3.4. Ergänzung zu [1; IV, §1, 2.2]
3.5. Äquivalente Schlüssel
3.6. Äquivalente F ∈
3.4. Ergänzung zu [1; IV, §1, 2.2]
3.5. Äquivalente Schlüssel
3.6. Äquivalente F ∈  3.7. Experimentelle Untersuchungen der statistischen
Eigenschaften der Additionsreihe
3.7.1. Allgemeine Programmbeschreibung
3.7.2. Beschreibung der Statistiken und Varianten
3.7.3. Zu erwartende Ergebnisse
3.7.4. Beobachtete Resultate
4. Ausführungen zu Kapitel V
4.1. Methoden zur Bestimmung des Schlüssels
4.2. Über Dekryptierbarkeit ohne Rekonstruktion
des Schlüssels
4.3. Der Einfluß der Blendnachrichten auf die krypto-
logischen Eigenschaften des Systems OPERATION
5. Zusammenfassung
Literatur
1. Einleitung
Bei der Analyse des Chiffrators des Systems OPERATION [1]
gelang es nicht, alle stark interessierenden Problem zu
lösen. Deshalb wurde die analytische Arbeit fortgesetzt.
Die neu erhaltenen theoretischen und experimentellen Ergeb-
nisse werden in dieser Ergänzung dargelegt. Außerdem werden
hier Präzisierungen, Korrekturen und Ergänzungen zum Text
der Analyse [1] vorgenommen.
Für die Lektüre der Ergänzung ist es notwendig, mit dieser
Analyse [1] bekannt zu sein, zumindestens mit den Paragraphen
und Punkten, zu denen die entsprechende Darlegung gehört.
Die Bezeichnungen bleiben unverändert, wenn nicht etwas
anders vorbehalten wurde. Hinweise werden auf folgende Art
gegeben:
[1; IV, §1, (2.2)] bezeichnet die Formel (2.2) des Para-
graphen 1 des IV. Kapitels der Analyse [1].
2. Darlegung zu den Kapiteln I - III
2.1. Bausteintechnik (siehe Einleitung)
Die Bausteinserie D 10 (alte Bezeichnung KME-10), die in
großem Umfang im K5-Muster (Versuchsmuster) verwendet
wird und zur Verwendung in der Serienproduktion vorge-
sehen ist, entspricht in den grundlegenden technischen
Parametern der Bausteinserie SN 74. Gegenwärtig wird die
Möglichkeit der Verwendung dieser Bausteine bei Tempera-
turen von -25 °C bis +85 °C (Serie E 10) untersucht.
2.2. Schema der Chiffrierverbindungen (s. Kap. I, §1)
Die Station A geht nicht in das Schema der Chiffrierver-
bindungen im System OPERATION ein. Die Nachrichten von
der Station A zur Station C werden im System KRISTALL-
QUARZ dechiffriert, danach in das System OPERATION über-
mittelt (automatisch) und in ihm für die Übermittlung
zur Station E dechiffriert.
2.3. Kryptologische Schaltung (s. Kap. III, §1.1)
Der Kommutator P realisiert eineindeutig die Verbindung
der Ausgänge vα mit den Eingängen uPα für α = 1,27 und
Pα = 1,27 und außerdem die Verbindung entweder von v28
mit u28 = uP28 und v29 = u29, P29 ∈ 1,27 oder v28
mit uP28, P28 ∈ 1,27 und v29 mit u28 = uP29.
Einige Verallgemeinerungen sind von technischer Seite
möglich.
2.4. Nachrichten (s. Kap. I, §2)
2.4.1. Klartext und Grundtext
Die Darstellung der Zahlen im BCD-Code 2421 wird durch
die Formel a4 * 2 + a3 * 4 + a2 * 2 + a1 * 1 verwirklicht,
d. h. 0 -0000, 1 - 0001, … 7 - 0111, 8 - 1110, 9 - 1111.
Wir bezeichnen den Grundtextblock mit G = (g1, g2, … , g47).
Dann ist g1 - laufende Nummer 1 "Löschen des Kommandos" -
das erste Bit im Kanal. Wir betrachten das Polynom
G(x) = g1x40 + g1x39 + … + g41.
Die Division
3.7. Experimentelle Untersuchungen der statistischen
Eigenschaften der Additionsreihe
3.7.1. Allgemeine Programmbeschreibung
3.7.2. Beschreibung der Statistiken und Varianten
3.7.3. Zu erwartende Ergebnisse
3.7.4. Beobachtete Resultate
4. Ausführungen zu Kapitel V
4.1. Methoden zur Bestimmung des Schlüssels
4.2. Über Dekryptierbarkeit ohne Rekonstruktion
des Schlüssels
4.3. Der Einfluß der Blendnachrichten auf die krypto-
logischen Eigenschaften des Systems OPERATION
5. Zusammenfassung
Literatur
1. Einleitung
Bei der Analyse des Chiffrators des Systems OPERATION [1]
gelang es nicht, alle stark interessierenden Problem zu
lösen. Deshalb wurde die analytische Arbeit fortgesetzt.
Die neu erhaltenen theoretischen und experimentellen Ergeb-
nisse werden in dieser Ergänzung dargelegt. Außerdem werden
hier Präzisierungen, Korrekturen und Ergänzungen zum Text
der Analyse [1] vorgenommen.
Für die Lektüre der Ergänzung ist es notwendig, mit dieser
Analyse [1] bekannt zu sein, zumindestens mit den Paragraphen
und Punkten, zu denen die entsprechende Darlegung gehört.
Die Bezeichnungen bleiben unverändert, wenn nicht etwas
anders vorbehalten wurde. Hinweise werden auf folgende Art
gegeben:
[1; IV, §1, (2.2)] bezeichnet die Formel (2.2) des Para-
graphen 1 des IV. Kapitels der Analyse [1].
2. Darlegung zu den Kapiteln I - III
2.1. Bausteintechnik (siehe Einleitung)
Die Bausteinserie D 10 (alte Bezeichnung KME-10), die in
großem Umfang im K5-Muster (Versuchsmuster) verwendet
wird und zur Verwendung in der Serienproduktion vorge-
sehen ist, entspricht in den grundlegenden technischen
Parametern der Bausteinserie SN 74. Gegenwärtig wird die
Möglichkeit der Verwendung dieser Bausteine bei Tempera-
turen von -25 °C bis +85 °C (Serie E 10) untersucht.
2.2. Schema der Chiffrierverbindungen (s. Kap. I, §1)
Die Station A geht nicht in das Schema der Chiffrierver-
bindungen im System OPERATION ein. Die Nachrichten von
der Station A zur Station C werden im System KRISTALL-
QUARZ dechiffriert, danach in das System OPERATION über-
mittelt (automatisch) und in ihm für die Übermittlung
zur Station E dechiffriert.
2.3. Kryptologische Schaltung (s. Kap. III, §1.1)
Der Kommutator P realisiert eineindeutig die Verbindung
der Ausgänge vα mit den Eingängen uPα für α = 1,27 und
Pα = 1,27 und außerdem die Verbindung entweder von v28
mit u28 = uP28 und v29 = u29, P29 ∈ 1,27 oder v28
mit uP28, P28 ∈ 1,27 und v29 mit u28 = uP29.
Einige Verallgemeinerungen sind von technischer Seite
möglich.
2.4. Nachrichten (s. Kap. I, §2)
2.4.1. Klartext und Grundtext
Die Darstellung der Zahlen im BCD-Code 2421 wird durch
die Formel a4 * 2 + a3 * 4 + a2 * 2 + a1 * 1 verwirklicht,
d. h. 0 -0000, 1 - 0001, … 7 - 0111, 8 - 1110, 9 - 1111.
Wir bezeichnen den Grundtextblock mit G = (g1, g2, … , g47).
Dann ist g1 - laufende Nummer 1 "Löschen des Kommandos" -
das erste Bit im Kanal. Wir betrachten das Polynom
G(x) = g1x40 + g1x39 + … + g41.
Die Division
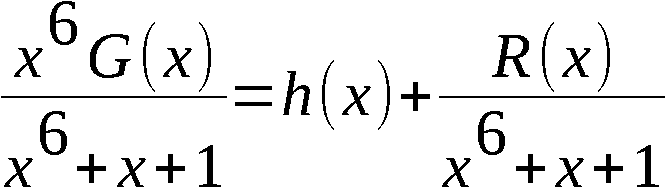 wo h(x) ein Polynom ist, liefert das Polynom
R(x) = g42x5 + g43x4 + … + g47, dessen Koeffizienten
Kontrollbits (Codesicherung I) sind.
2.4.2. Informationsblock
Das Kontrollbit für die Aussage "Chiffrierung normal" wird
nicht benutzt. Dieses Bit hat den festen Wert Null.
2.4.3. Bildung der Blendnachrichten
Der sogenannte Übernahmespeicher im Datensender, der den
Klartextblock enthält und diesen Block in die Chiffrier-
einrichtung übergibt, wird sofort nach Beendigung dieser
Übermittlung automatisch in ein rückgekoppeltes Schiebe-
register mit einer Frequenz von 100 kHz umgeschaltet.
Der Klartexblock wird rekurrent mit dem Polynom X41 + x38 + 1
umgeformt.
Wenn die Taste
wo h(x) ein Polynom ist, liefert das Polynom
R(x) = g42x5 + g43x4 + … + g47, dessen Koeffizienten
Kontrollbits (Codesicherung I) sind.
2.4.2. Informationsblock
Das Kontrollbit für die Aussage "Chiffrierung normal" wird
nicht benutzt. Dieses Bit hat den festen Wert Null.
2.4.3. Bildung der Blendnachrichten
Der sogenannte Übernahmespeicher im Datensender, der den
Klartextblock enthält und diesen Block in die Chiffrier-
einrichtung übergibt, wird sofort nach Beendigung dieser
Übermittlung automatisch in ein rückgekoppeltes Schiebe-
register mit einer Frequenz von 100 kHz umgeschaltet.
Der Klartexblock wird rekurrent mit dem Polynom X41 + x38 + 1
umgeformt.
Wenn die Taste Blendtext
gedrückt wird, werden 40 Bit der
Rekursion, die im Speicher sind, in die Chiffriereinrichtung
übergeben und bilden zusammen mit der 'Blendkennung' den
Blendklartextblock, der analog zu anderen Klartextblöcken
abgearbeietet wird. Der Übernahmespeicher arbeitet in dieser
Zeit rekursiv weiter mit einer Frequenz von 100 kHz, und nach
30 Übertragungstakten übermittelt er wieder 40 Bit der Rekur-
sion in die Chiffriereinrichtung und so weiter 5 sek. lang.
Durch wiederholten Tastendruck kann man erreichen, daß die
Übermittlung von Blendblöcken länger als 5 sek. andauert.
Blendnachrichten haben den niedrigsten Rang.
3. Darlegung zu Kapitel IV
3.1. Zerlegung der Abbildung ϕ(0,0,0) in Zyklen
Für feste Parameter (u0),s,r) kann man die Abbildung
ϕ(u0),s,r) als Permutation der Menge  betrachten
und in Zyklen zerlegen. Mit Hilfe einer EDVA werden für
(P,R) = (P0,R0) fünf Zyklen gefunden, deren Längen
92209323, 32830171, 6282627, 1468372, 950434
betragen. (Ausführliche Resultate siehe [2].)
Außerdem existiert ein Zyklus der Länge 1 - ein Fixpunkt
[1; IV, §1, 3.1.].
Alle Elemente, die in einem Zyklus auftreten, liegen in
einer Zustandsklasse. Damit wurde bewiesen, daß für
(P0,R0) sehr große Zustandsklassen existieren, und es
wurden Abschätzungen der Anzahl der Elemente von unten
in diesen Klassen gefunden. Es wird angenommen, daß alle
Zustände eine einzige Klasse bilden.
3.2. Korrektur zu [1; IV, §2, 1.]
Die Teilmenge
betrachten
und in Zyklen zerlegen. Mit Hilfe einer EDVA werden für
(P,R) = (P0,R0) fünf Zyklen gefunden, deren Längen
92209323, 32830171, 6282627, 1468372, 950434
betragen. (Ausführliche Resultate siehe [2].)
Außerdem existiert ein Zyklus der Länge 1 - ein Fixpunkt
[1; IV, §1, 3.1.].
Alle Elemente, die in einem Zyklus auftreten, liegen in
einer Zustandsklasse. Damit wurde bewiesen, daß für
(P0,R0) sehr große Zustandsklassen existieren, und es
wurden Abschätzungen der Anzahl der Elemente von unten
in diesen Klassen gefunden. Es wird angenommen, daß alle
Zustände eine einzige Klasse bilden.
3.2. Korrektur zu [1; IV, §2, 1.]
Die Teilmenge  muß in der folgenden Weise definiert
werden:
muß in der folgenden Weise definiert
werden:
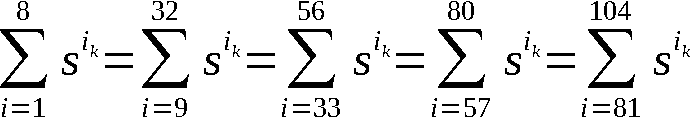 (k = 1,2).
siehe [1; III, §2,1.]
3.3. Die logischen Funktionen h
(k = 1,2).
siehe [1; III, §2,1.]
3.3. Die logischen Funktionen h In [1; IV, §2, 4.] wurde die Möglichkeit der Darstellung
der Komponenten h
In [1; IV, §2, 4.] wurde die Möglichkeit der Darstellung
der Komponenten h des Vektors Ui als logische Funktionen
h
des Vektors Ui als logische Funktionen
h , deren Veränderliche die Komponenten von U0,S,F sind,
und ihre Berechenbarkeit auf einer EDVA gezeigt.
Von uns wird ein Programm zur Berechnung von h
, deren Veränderliche die Komponenten von U0,S,F sind,
und ihre Berechenbarkeit auf einer EDVA gezeigt.
Von uns wird ein Programm zur Berechnung von h für
(P,R) = (P0,R0) und U0 = (000 000 011 011 111 111 100 000 000)
[1; Zusammenfassung, 3.2] für alle α=1,27
und i = 1,i0 erarbeitet, wobei i0 so gewählt wurde, daß die
Funktion h
für
(P,R) = (P0,R0) und U0 = (000 000 011 011 111 111 100 000 000)
[1; Zusammenfassung, 3.2] für alle α=1,27
und i = 1,i0 erarbeitet, wobei i0 so gewählt wurde, daß die
Funktion h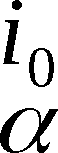 nicht riesig und überschaubar sind. Es
wird erwartet, daß i0 etwa 10 - 20 angenommen werden kann.
Die Berechnung nach diesem Programm soll eine Vorstellung
über die Kompliziertheit der Funktion h
nicht riesig und überschaubar sind. Es
wird erwartet, daß i0 etwa 10 - 20 angenommen werden kann.
Die Berechnung nach diesem Programm soll eine Vorstellung
über die Kompliziertheit der Funktion h für kleine i,
über den Zeitaufwand zur Berechnung und das Speichervolumen
geben. Außerdem müssen Gesetzmäßigkeiten in diesen Funktio-
nen gesucht werden. Möglicherweise läßt sich eine Abschä-
tzung der Anzahl der Zustandsklassen erhalten.
In Abhängigkeit von diese Ergebnissen werden Programm
zur Berechnung von h
für kleine i,
über den Zeitaufwand zur Berechnung und das Speichervolumen
geben. Außerdem müssen Gesetzmäßigkeiten in diesen Funktio-
nen gesucht werden. Möglicherweise läßt sich eine Abschä-
tzung der Anzahl der Zustandsklassen erhalten.
In Abhängigkeit von diese Ergebnissen werden Programm
zur Berechnung von h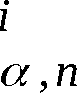 für n = 2 und i = 104, 208, …
sowie zur Berechnung von h
für n = 2 und i = 104, 208, …
sowie zur Berechnung von h , wobei einige Veränderliche
festgehalten werden, z. B. F = (f2, f3, f1, 0, … , 0) und
gegebenenfalls andere Programme erarbeitet werden.
3.4. Ergänzung zu [1; IV, §1, 2.2]
(N10) es muß eine der folgenden Gleichungen erfüllt sein:
P6 = 27, P13 = 27, P20 = 27, P27 = 27.
Beweis: Sei irgend ein Paar (P,R) mit der Eigenschaft
P21 = 27 festgehalten.
Stellen wir die Funktion Z in der Weise dar:
Z(e1, e2, …, e6) = e1z1(e2, … , e6) + z2(e2, … , e6).
Diese Darstellung ist eindeutig. Es existieren ein Tupel:
(e2, … , e6) ∈ {0,1}5, für das z1 = 0 ist.
Wir betrachten die Formel (1.1.) für ɳ = R9:
Y3R9-2 = u3R9 - 3 + r + s + z(s,uP1, …, uP5) + UP6 +
+ z(uP7, …) + uP13 + z(uP14, …) + uP20 +
+ u27z1(uP22, …, uP26) + z2(uP22, …, uP26) + uP27.
Es existieren U1 ∈
, wobei einige Veränderliche
festgehalten werden, z. B. F = (f2, f3, f1, 0, … , 0) und
gegebenenfalls andere Programme erarbeitet werden.
3.4. Ergänzung zu [1; IV, §1, 2.2]
(N10) es muß eine der folgenden Gleichungen erfüllt sein:
P6 = 27, P13 = 27, P20 = 27, P27 = 27.
Beweis: Sei irgend ein Paar (P,R) mit der Eigenschaft
P21 = 27 festgehalten.
Stellen wir die Funktion Z in der Weise dar:
Z(e1, e2, …, e6) = e1z1(e2, … , e6) + z2(e2, … , e6).
Diese Darstellung ist eindeutig. Es existieren ein Tupel:
(e2, … , e6) ∈ {0,1}5, für das z1 = 0 ist.
Wir betrachten die Formel (1.1.) für ɳ = R9:
Y3R9-2 = u3R9 - 3 + r + s + z(s,uP1, …, uP5) + UP6 +
+ z(uP7, …) + uP13 + z(uP14, …) + uP20 +
+ u27z1(uP22, …, uP26) + z2(uP22, …, uP26) + uP27.
Es existieren U1 ∈  und U2 ∈
und U2 ∈  , die sich nur in der
Komponente u27 unterscheiden, für die Z1 = 0 ist. Für diese
nimmt y3R9-2 ein und denselben wert an und ebenso alle
übrigen Komponenten yɳ.
Das widerspricht der Eineindeutigkeit.
Analog läßt sich für die übrigen 22 Fälle ein Widerspruch
herleiten.
3.5. Äquivalente Schlüssel
3.5.1. Äquivalente Schlüssel bezüglich UN für (P0,R0)
Sei (P,R) = (P0,R0), und wir betrachten den speziell
ausgewählten Wert U = (000 001 000 100 100 100 100 100 000).
Für diesen U ∈
, die sich nur in der
Komponente u27 unterscheiden, für die Z1 = 0 ist. Für diese
nimmt y3R9-2 ein und denselben wert an und ebenso alle
übrigen Komponenten yɳ.
Das widerspricht der Eineindeutigkeit.
Analog läßt sich für die übrigen 22 Fälle ein Widerspruch
herleiten.
3.5. Äquivalente Schlüssel
3.5.1. Äquivalente Schlüssel bezüglich UN für (P0,R0)
Sei (P,R) = (P0,R0), und wir betrachten den speziell
ausgewählten Wert U = (000 001 000 100 100 100 100 100 000).
Für diesen U ∈  erhalten wir Z = (s2 + 1, 0, 0, 0, s1 + 1)
mit den Bezeichnungen von [1; IV, §3, 3.2]. Folglich ist
die hinreichende Bedingung für die Nichtexistenz äquivalen-
ter Schlüssel erfüllt.
Seien v = 1 und μ = 52, so finden wir, daß nicht weni-
ger als 2104 paarweise verschiedene Schlüssel S ∈
erhalten wir Z = (s2 + 1, 0, 0, 0, s1 + 1)
mit den Bezeichnungen von [1; IV, §3, 3.2]. Folglich ist
die hinreichende Bedingung für die Nichtexistenz äquivalen-
ter Schlüssel erfüllt.
Seien v = 1 und μ = 52, so finden wir, daß nicht weni-
ger als 2104 paarweise verschiedene Schlüssel S ∈  existieren, die nichtäquivalent bezüglich U104 sind.
Auf der Grundlage der Folgerung am Schluß des Punktes
3.1 kann man folgern, daß nicht weniger als 2104 paarweise
verschiedene Schlüssel S ∈
existieren, die nichtäquivalent bezüglich U104 sind.
Auf der Grundlage der Folgerung am Schluß des Punktes
3.1 kann man folgern, daß nicht weniger als 2104 paarweise
verschiedene Schlüssel S ∈  existieren, die nicht äquvia-
lent bezüglich der Folge (U104i)
existieren, die nicht äquvia-
lent bezüglich der Folge (U104i) für beliebiges natür-
liches N sind, wenn man diese Art von Äquivalenz für alle
U0 ∈
für beliebiges natür-
liches N sind, wenn man diese Art von Äquivalenz für alle
U0 ∈  definiert.
3.5.2. Äquivalente Schlüssel bezüglich der Additionsreihe
Aus allen erhaltenen Ergebnissen darf man keine direkten
Schlüsse über äquivalente Schlüssel bezüglich der Addi-
tionsreihe ziehen, obgleich nach allen heuristischen
Schlüssen die Lage positiv einzuschätzen ist. Trotz aller
Bemühungen konnte kein annehmbarer theoretischer Weg zu
dem Problem äquivalente Schlüssel bezüglich der Additions-
reihe gefunden werden, welches in der vorliegenden Ana-
lyse nach dem gegenwärtigen Stand des Wissens über die
Chiffrierabbilung als das wichtigste Problem angesehen
wird.
Berücksichtigt man die Möglichkeit der zur Verfügung
stehenden Rechentechnik, so kann man nicht mehr als 107
paarweise verschiedene Schlüssel experimentell auf Äquiva-
lenz prüfen, was im Vergleich mit |
definiert.
3.5.2. Äquivalente Schlüssel bezüglich der Additionsreihe
Aus allen erhaltenen Ergebnissen darf man keine direkten
Schlüsse über äquivalente Schlüssel bezüglich der Addi-
tionsreihe ziehen, obgleich nach allen heuristischen
Schlüssen die Lage positiv einzuschätzen ist. Trotz aller
Bemühungen konnte kein annehmbarer theoretischer Weg zu
dem Problem äquivalente Schlüssel bezüglich der Additions-
reihe gefunden werden, welches in der vorliegenden Ana-
lyse nach dem gegenwärtigen Stand des Wissens über die
Chiffrierabbilung als das wichtigste Problem angesehen
wird.
Berücksichtigt man die Möglichkeit der zur Verfügung
stehenden Rechentechnik, so kann man nicht mehr als 107
paarweise verschiedene Schlüssel experimentell auf Äquiva-
lenz prüfen, was im Vergleich mit | | ≈ 1059 zu
wenig ist. Unter Beachtung der Möglichkeiten der technischen
Realisierung kann man Abänderungen in der kryptologischen
Schaltung durchführen, z. B. je 104 Elemente der Folge
(u
| ≈ 1059 zu
wenig ist. Unter Beachtung der Möglichkeiten der technischen
Realisierung kann man Abänderungen in der kryptologischen
Schaltung durchführen, z. B. je 104 Elemente der Folge
(u ) addieren:
) addieren:
 , i = 1,47
Leider vereinfacht sich durch solche Änderung die
Aufgabe nicht.
Man kann versuchen, theoretisch und experimentell verein-
fachte Modelle der kryptologischen Schaltung zu untersuchen.
Es ist jedoch kein Weg sichtbar, die in solchen Modellen
erhaltenen Ergebnisse zu verallgemeinern.
Aus den aufgezeigten Gründen wird das Problem der äquiva-
lenten Schlüssel im Chiffrator des Systems OPERATION
nicht weiter untersucht.
3.6. Äquivalente F ∈
, i = 1,47
Leider vereinfacht sich durch solche Änderung die
Aufgabe nicht.
Man kann versuchen, theoretisch und experimentell verein-
fachte Modelle der kryptologischen Schaltung zu untersuchen.
Es ist jedoch kein Weg sichtbar, die in solchen Modellen
erhaltenen Ergebnisse zu verallgemeinern.
Aus den aufgezeigten Gründen wird das Problem der äquiva-
lenten Schlüssel im Chiffrator des Systems OPERATION
nicht weiter untersucht.
3.6. Äquivalente F ∈  Im Chiffriersystem wird nur Zeitschlüssel verwendet. Mit
der Folge (fi)i wird erreicht, daß zu verschiedenen Zeit-
punkten für ein und denselben Schlüssel in der Regel ver-
scheidene Additionsreihen erzeugt werden. Dieser wesent-
liche kryptologische Effekt wird abgeschwächt, wenn ver-
schiendene Abschnitte der Folge (fi)i für beliebige Schlüs-
sel ein und dieselbe Additionsreihe erzeugen.
(Wir bemerken, daß aufgrund
|
Im Chiffriersystem wird nur Zeitschlüssel verwendet. Mit
der Folge (fi)i wird erreicht, daß zu verschiedenen Zeit-
punkten für ein und denselben Schlüssel in der Regel ver-
scheidene Additionsreihen erzeugt werden. Dieser wesent-
liche kryptologische Effekt wird abgeschwächt, wenn ver-
schiendene Abschnitte der Folge (fi)i für beliebige Schlüs-
sel ein und dieselbe Additionsreihe erzeugen.
(Wir bemerken, daß aufgrund
| | = s52 - 1 < 247 = |{0,1}47|
für festes S gewiß solche Abschnitte existieren.)
Definition:
Zwei Elemente F ∈
| = s52 - 1 < 247 = |{0,1}47|
für festes S gewiß solche Abschnitte existieren.)
Definition:
Zwei Elemente F ∈  und F' ∈
und F' ∈  heißen äquivalent bezüglich
der Additionsreihe der Länge L, wenn für festes U ∈
heißen äquivalent bezüglich
der Additionsreihe der Länge L, wenn für festes U ∈  ,
für alle S ∈
,
für alle S ∈  gilt ΨL(U,S,F) = ΨL(U,S,F').
Es besteht eine gewisse Analogie zu den äquivalenten
Schlüsseln, aber natürlich auch Besonderheiten. Analog
zu den äquivalenten Schlüsseln konnten überhaupt keine
Ergebnisse bei der Untersuchung der Äquivalenz bezüglich
der Additionsreihe erreicht werden, aber bezüglich ande-
rer Arten der Äquivalenz kann man gewisse Gesetzmäßig-
keiten exakt nachweisen.
Man kann zum Beispiel analog zu [1; IV, §3, 3.1] die
Äquivalenz bezüglich UN definieren.
Der dort dargelegte Gang der Überlegung wird mit gewis-
sen unwesentlichen Änderungen übernommen. Man erhält
wieder die Formel (3.5).
Hier ist jedoch ein Unterschied; Die notwendige Bedingung
der Existenz äquivalenter Schlüssel verlangt, daß Paare
(s1, s2) ≠ (s
gilt ΨL(U,S,F) = ΨL(U,S,F').
Es besteht eine gewisse Analogie zu den äquivalenten
Schlüsseln, aber natürlich auch Besonderheiten. Analog
zu den äquivalenten Schlüsseln konnten überhaupt keine
Ergebnisse bei der Untersuchung der Äquivalenz bezüglich
der Additionsreihe erreicht werden, aber bezüglich ande-
rer Arten der Äquivalenz kann man gewisse Gesetzmäßig-
keiten exakt nachweisen.
Man kann zum Beispiel analog zu [1; IV, §3, 3.1] die
Äquivalenz bezüglich UN definieren.
Der dort dargelegte Gang der Überlegung wird mit gewis-
sen unwesentlichen Änderungen übernommen. Man erhält
wieder die Formel (3.5).
Hier ist jedoch ein Unterschied; Die notwendige Bedingung
der Existenz äquivalenter Schlüssel verlangt, daß Paare
(s1, s2) ≠ (s ,s
,s ) mit der Eigenschaft (3.5) existieren,
aber die notwendige Bedingung der Existenz äquivalenter F
verlangt, daß für alle (s1,s2) ≠ (s
) mit der Eigenschaft (3.5) existieren,
aber die notwendige Bedingung der Existenz äquivalenter F
verlangt, daß für alle (s1,s2) ≠ (s ,s
,s ) die Eigenschaft
(3.5) erfüllt ist.
In der weiteren Untersuchung dieses Problems spielt die
Menge {ϕ-1ϕU} (über sie siehe [1; IV, §1, 4.3])
eine Rolle.
3.7. Experimentelle Untersuchung der statistischen
Eigenschaften der Additionsreihen
3.7.1. Allgemeine Programmbeschreibung
Das erarbeitete Programm für eine EDVA realisiert die in
[1; IV, §2, 1.] beschriebene kryptologische Schaltung
und erzeugt Additionsreihen AL = (ai)
) die Eigenschaft
(3.5) erfüllt ist.
In der weiteren Untersuchung dieses Problems spielt die
Menge {ϕ-1ϕU} (über sie siehe [1; IV, §1, 4.3])
eine Rolle.
3.7. Experimentelle Untersuchung der statistischen
Eigenschaften der Additionsreihen
3.7.1. Allgemeine Programmbeschreibung
Das erarbeitete Programm für eine EDVA realisiert die in
[1; IV, §2, 1.] beschriebene kryptologische Schaltung
und erzeugt Additionsreihen AL = (ai) = 1.
Dabei ist (P,R) = P0,R0) festgelegt, U0 ∈
= 1.
Dabei ist (P,R) = P0,R0) festgelegt, U0 ∈  - belie-
big, S ∈
- belie-
big, S ∈  - beliebig, α ∈ 1,27 - beliebig.
Das Programm verfährt auf die Weise, daß U0, S, α und
L festgelegt werden und mit ihnen N Additionsreihen AL
berechnet werden, wobei zufällig hergestellte F ∈
- beliebig, α ∈ 1,27 - beliebig.
Das Programm verfährt auf die Weise, daß U0, S, α und
L festgelegt werden und mit ihnen N Additionsreihen AL
berechnet werden, wobei zufällig hergestellte F ∈  benutzt
werden.
Diese N Additionsreihen sind der unten beschriebenen
statistischen Auswertung mit den Varianten A, B, C, D,
E unterworfen.
Mit Hilfe eines Pseudo-Zufallsgenerators mit der Formel
Xi = (165+1)Xi-1 + b(mod 1613), wobei b eine ungerade
Konstante ist, werden die zufälligen F erzeugt.
Aus der Literatur ist bekannt, daß für beliebiges
x0 ∈ 0, 1613 - 1 die Folge (xi)i gute statistische
Eigenschaften besitzt.
Der Wert x0 ergibt sich automatisch durch Ausnutzung der
Uhr in der EDVA und des Datums. Damit garantiert,
daß sich bei richtiger Arbeit des Programms keine x0-Wert
im Lauf eines Jahres wiederholen kann.
Schließlich wird (yi)i = 1,2,.. = (x3i)i=1,2,…
gebildet. Die werte yi sind die zufälligen F.
3.7.2. Beschreibung der Statistiken und Varianten
Definieren wir Zahlencharakteristiken der Additionsreihe
AL = (ai)
benutzt
werden.
Diese N Additionsreihen sind der unten beschriebenen
statistischen Auswertung mit den Varianten A, B, C, D,
E unterworfen.
Mit Hilfe eines Pseudo-Zufallsgenerators mit der Formel
Xi = (165+1)Xi-1 + b(mod 1613), wobei b eine ungerade
Konstante ist, werden die zufälligen F erzeugt.
Aus der Literatur ist bekannt, daß für beliebiges
x0 ∈ 0, 1613 - 1 die Folge (xi)i gute statistische
Eigenschaften besitzt.
Der Wert x0 ergibt sich automatisch durch Ausnutzung der
Uhr in der EDVA und des Datums. Damit garantiert,
daß sich bei richtiger Arbeit des Programms keine x0-Wert
im Lauf eines Jahres wiederholen kann.
Schließlich wird (yi)i = 1,2,.. = (x3i)i=1,2,…
gebildet. Die werte yi sind die zufälligen F.
3.7.2. Beschreibung der Statistiken und Varianten
Definieren wir Zahlencharakteristiken der Additionsreihe
AL = (ai) , welche durch das Programm berechnet werden.
Wir bezeichnen durch A
, welche durch das Programm berechnet werden.
Wir bezeichnen durch A , j = 1,N, die Additionsreihen,
die mit einem Schlüssel berechnet werden.
t1(AL) =
, j = 1,N, die Additionsreihen,
die mit einem Schlüssel berechnet werden.
t1(AL) =  - Anzahl der Einsen in AL.
T1 =
- Anzahl der Einsen in AL.
T1 =  .
t2,k(AL), K = 0,31 - Anzahl der Polygramme der Länge 5
derselben Art in AL, wobei eine Überlappung zugelassen
ist. (d. h., es werden alle Tupel aiai+1ai+3ai+3ai+4)
für alle i = 1,L-4 berücksichtigt.)
T2K =
.
t2,k(AL), K = 0,31 - Anzahl der Polygramme der Länge 5
derselben Art in AL, wobei eine Überlappung zugelassen
ist. (d. h., es werden alle Tupel aiai+1ai+3ai+3ai+4)
für alle i = 1,L-4 berücksichtigt.)
T2K = 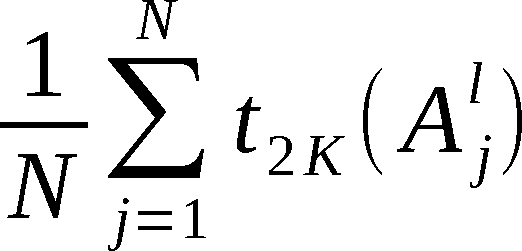 t3K(AL), K = 1,L - Anzahl der Serien (der maximalen
Teilfolge gleicher Elemente) der Länge K in AL.
t30(AL) - Anzahl der Serien in AL, deren Länge
über K hinausgeht, K ist eine feste Zahl aus dem Intervall
1,L-1.
T3K =
t3K(AL), K = 1,L - Anzahl der Serien (der maximalen
Teilfolge gleicher Elemente) der Länge K in AL.
t30(AL) - Anzahl der Serien in AL, deren Länge
über K hinausgeht, K ist eine feste Zahl aus dem Intervall
1,L-1.
T3K =  , K = 0,L.
t4(AL) =
, K = 0,L.
t4(AL) = 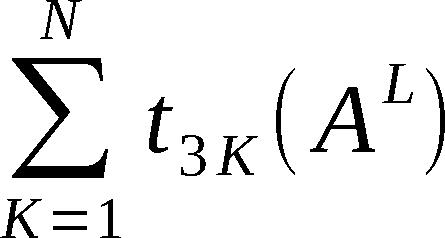 (Anzahl der Serein in AL)
T4 =
(Anzahl der Serein in AL)
T4 = 
| t5(A47) = | { | t1(A47) | ≤ 23 | , t1(F) | ≤ 25 |
| ≤23 | ≥ 26 |
| ≥24 | ≤ 25 |
| ≥24 | ≥ 26, |
wobei A47 gerade mit dem F ∈  gebildet wird, für welches
t1(F) - Anzahl der Einsen in F = (f1, f2, …, f52) - be-
rechnet wird.
T5K =
gebildet wird, für welches
t1(F) - Anzahl der Einsen in F = (f1, f2, …, f52) - be-
rechnet wird.
T5K = 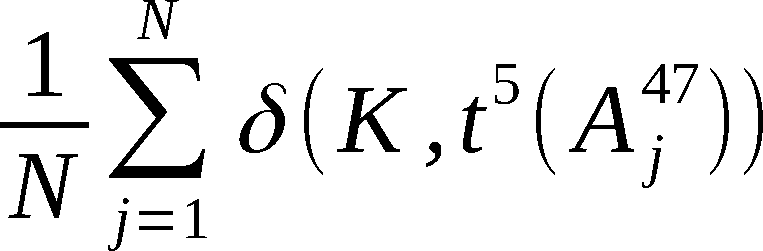 , K = 0,3,
wobei δ(a,b) das Kronecker - Symbol (δ(a,a) = 1,δ(a,b) = 0)
für a≠b).
, K = 0,3,
wobei δ(a,b) das Kronecker - Symbol (δ(a,a) = 1,δ(a,b) = 0)
für a≠b).
| t6(A1) = | { | 0 | a1 = a1 = 0 |
| 1 | a1 = 0, 11 = 1 |
| 2 | a1 = 1, 11 = 0 |
| 3 | a1 = a1 = 1, |
wobei a1 mit Hilfe von F = (f1,f2, …, f51, f52) gebil-
det wird, und a1 mit Hilfe von F = (f1, f2, …, f51, f52+1).
T6K = 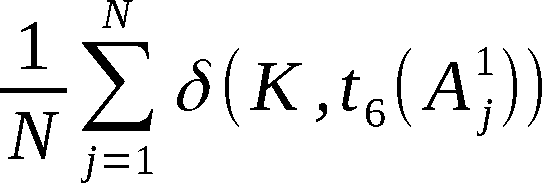 , K = 0,3.
Das Programm läßt folgende Varianten zu:
Varianten A und B
T1, T2K (K = 0,31), T3K (K = 0,K), T4 werden für
L = 47 (A) oder 48 ≤ L ≤ 10 000(B) berechnet und ausge-
geben.
Außerdem werden folgende Werte berechnet und ausgegeben:
, K = 0,3.
Das Programm läßt folgende Varianten zu:
Varianten A und B
T1, T2K (K = 0,31), T3K (K = 0,K), T4 werden für
L = 47 (A) oder 48 ≤ L ≤ 10 000(B) berechnet und ausge-
geben.
Außerdem werden folgende Werte berechnet und ausgegeben:
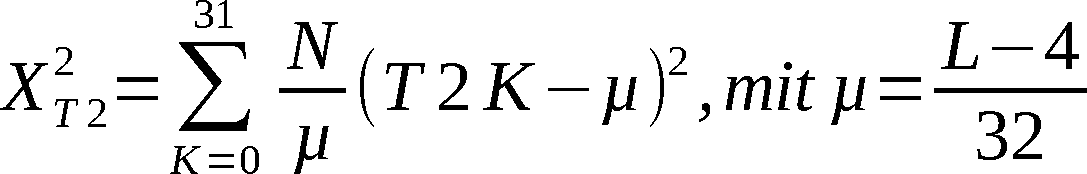 ;
;
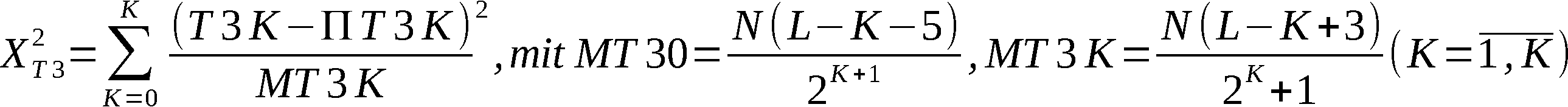 ;
T2(δ), δ = 1, 2, 3 - die Zahl der Werte T2K im Intervall
;
T2(δ), δ = 1, 2, 3 - die Zahl der Werte T2K im Intervall
 .
Variante C
Sie berechnet und gibt aus T1 für L = 1.
Variante D
Sie berechnet und gibt aus T5K, K = 0,3, für L = 47.
Variante E
Sie berchnet und gibt aus T6K, K = 0,3 für L = 1.
3.7.3. Zu erwartende Ergebnisse
Es wird erwartet, daß die Additionsreihen die statistischen
Eigenschaften zufälliger, gleichwahrscheinlicher, vonein-
ander und von F unabhängiger Folgen aufweisen. Das ist die
Grundhypothese, die durch die oben aufzeigten Statistiken
geprüft wird.
Sei AL ein Zufallsvektor, der alle 2L Werte aus {0,1}L
gleichwahrscheinlich annimmt. Analog sei F ein Zufallsvek-
tor, der alle 252 Werte aus
.
Variante C
Sie berechnet und gibt aus T1 für L = 1.
Variante D
Sie berechnet und gibt aus T5K, K = 0,3, für L = 47.
Variante E
Sie berchnet und gibt aus T6K, K = 0,3 für L = 1.
3.7.3. Zu erwartende Ergebnisse
Es wird erwartet, daß die Additionsreihen die statistischen
Eigenschaften zufälliger, gleichwahrscheinlicher, vonein-
ander und von F unabhängiger Folgen aufweisen. Das ist die
Grundhypothese, die durch die oben aufzeigten Statistiken
geprüft wird.
Sei AL ein Zufallsvektor, der alle 2L Werte aus {0,1}L
gleichwahrscheinlich annimmt. Analog sei F ein Zufallsvek-
tor, der alle 252 Werte aus  gleichwahrscheinlich annimmt.
Dann sind t1, T1, t2k usw. Zufallsgrößen, deren Wahrschein-
lichkeitsverteilung eindeutig definiert ist.
Wir bezeichnen durch p(ξ = x) die Wahrscheinlichkeit da-
f+r, daß die Zufallsgröße ξ den Wert x annimmt, durch Mξ
die mathematische Erwartung und durch Dξ die Dispersion
der Zufallsgröße ξ.
Es nehme ξ die Werte x1,x2, …, xn mit den entsprechen-
den Wahrscheinlichkeiten p1, p2, …, pn an. Dann gilt
nach Definition:
Mξ =
gleichwahrscheinlich annimmt.
Dann sind t1, T1, t2k usw. Zufallsgrößen, deren Wahrschein-
lichkeitsverteilung eindeutig definiert ist.
Wir bezeichnen durch p(ξ = x) die Wahrscheinlichkeit da-
f+r, daß die Zufallsgröße ξ den Wert x annimmt, durch Mξ
die mathematische Erwartung und durch Dξ die Dispersion
der Zufallsgröße ξ.
Es nehme ξ die Werte x1,x2, …, xn mit den entsprechen-
den Wahrscheinlichkeiten p1, p2, …, pn an. Dann gilt
nach Definition:
Mξ = 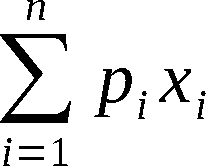 und Dξ = M(ξ - Mξ)2.
Mit der Statistik T1 wird die Häufigkeit des Auftretens
der Eins in den Additionsreihen geprüft. Es ist
p(t1 = x) =
und Dξ = M(ξ - Mξ)2.
Mit der Statistik T1 wird die Häufigkeit des Auftretens
der Eins in den Additionsreihen geprüft. Es ist
p(t1 = x) = 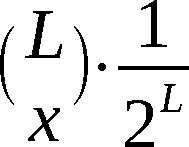 x = 0,L
p(NT1 = x) =
x = 0,L
p(NT1 = x) = 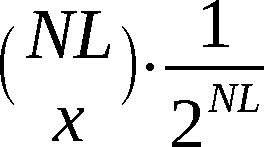 x = 0,NL
woraus folgt MT1 = L/2, DT1 = L/4N.
Der beobachtete Wert T1 muß die Wahrscheinlichkeit ≈ 68 %
im Intervall [
x = 0,NL
woraus folgt MT1 = L/2, DT1 = L/4N.
Der beobachtete Wert T1 muß die Wahrscheinlichkeit ≈ 68 %
im Intervall [ ], mit Wahrscheinlichkeit
≈ 96 % im Intervall [
], mit Wahrscheinlichkeit
≈ 96 % im Intervall [ ] und mit Wah-
scheinlichkeit ≈ 97 % im Intervall [
] und mit Wah-
scheinlichkeit ≈ 97 % im Intervall [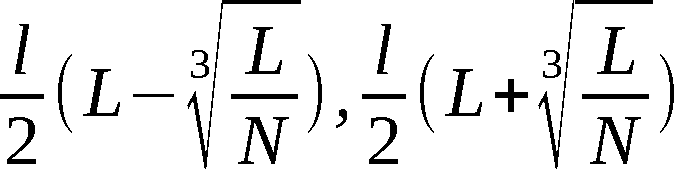 ]
liegen.
Die Statistik T2K überprüft die Häufigkeit des Auftretens
der Polygramme der Länge 5. Abweichungen von den theoretischen
Werten würden, bei Übereinstimmung der theoretischen und beobach-
teten Werte für T1, auf Abhängigkeit zwischen aufeinander-
folgenden Additionseinheiten schließen lassen. Betrachten wir die
Zufallsgröße t2K für festes K. Wenn man aufeinanderfolgende
Polygramme in AL als unabhängig voneinander ansieht (was nicht
ganz korrekt ist), so kann man die Binominalverteilung annehmen:
p(t2,K = x) =
]
liegen.
Die Statistik T2K überprüft die Häufigkeit des Auftretens
der Polygramme der Länge 5. Abweichungen von den theoretischen
Werten würden, bei Übereinstimmung der theoretischen und beobach-
teten Werte für T1, auf Abhängigkeit zwischen aufeinander-
folgenden Additionseinheiten schließen lassen. Betrachten wir die
Zufallsgröße t2K für festes K. Wenn man aufeinanderfolgende
Polygramme in AL als unabhängig voneinander ansieht (was nicht
ganz korrekt ist), so kann man die Binominalverteilung annehmen:
p(t2,K = x) =  , x = 0,L-4
Dann ist
Mt2K =
, x = 0,L-4
Dann ist
Mt2K = 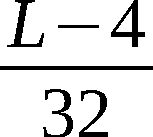 , Dt2K =
, Dt2K =  ,
woraus bei Betrachtung der Summe NT2K unabhängiger Zufalls-
größen folgt
MT2K =
,
woraus bei Betrachtung der Summe NT2K unabhängiger Zufalls-
größen folgt
MT2K = 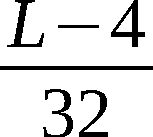 , DT2K =
, DT2K =  ; K = 0,31.
Analog zu T1 kann man entsprechende Intervalle angeben
(sogenannte δ - Bereiche):
; K = 0,31.
Analog zu T1 kann man entsprechende Intervalle angeben
(sogenannte δ - Bereiche):
 , δ = 1,2,3
In denen der Wert T2K mit der angegebenen Wahrscheinlichkeit
(68%, 96%, 99,7%) liegen muß.
Indem wir die Gleichberechtigung aller T2K bzgl. K berücksichtigen
und die als unabhängig ansehen, kann man den Ausdruck
, δ = 1,2,3
In denen der Wert T2K mit der angegebenen Wahrscheinlichkeit
(68%, 96%, 99,7%) liegen muß.
Indem wir die Gleichberechtigung aller T2K bzgl. K berücksichtigen
und die als unabhängig ansehen, kann man den Ausdruck
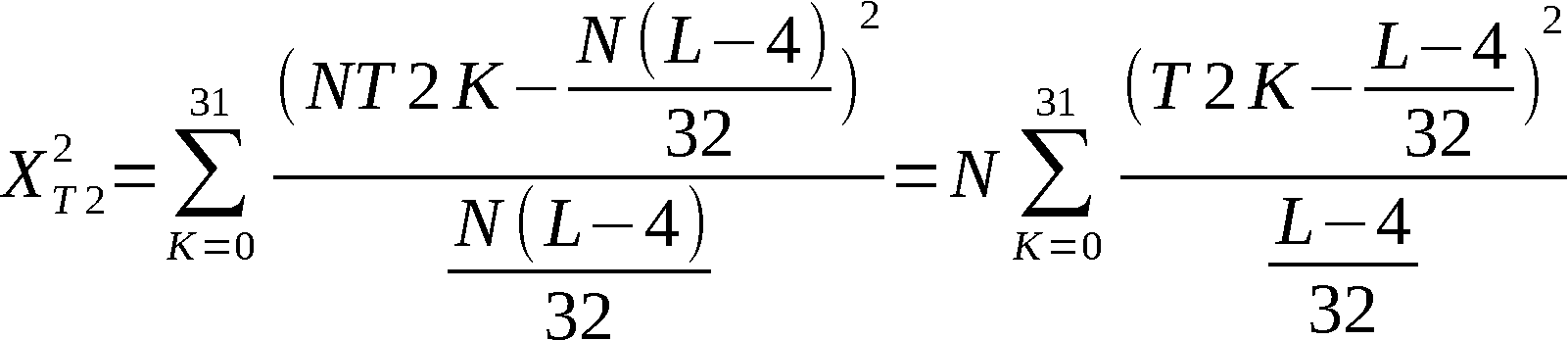 betrachten, der für N → ∞ gegen die X2-Verteilung mit
31 Freiheitsgraden strebt. Aus der Literatur ist bekannt
[3, Seite 551], daß für diese Verteilung sein muß:
mit Wahrscheinlichkeit ≈ 50 % X2 ≤ 30
mit Wahrscheinlichkeit ≈ 95 % X2 ≤ 46
mit Wahrscheinlichkeit ≈ 99 % X2 ≤ 52.
Auf Abhängigkeiten zwischen aufeinanderfolgenden Additions-
einheiten würden auch Abweichungen von den theoretischen Werten
der Statistiken T3K hingewiesen.
Die Verteilung der Größen t3K wurde in [4] untersucht.
Es gilt
Mt3K =
betrachten, der für N → ∞ gegen die X2-Verteilung mit
31 Freiheitsgraden strebt. Aus der Literatur ist bekannt
[3, Seite 551], daß für diese Verteilung sein muß:
mit Wahrscheinlichkeit ≈ 50 % X2 ≤ 30
mit Wahrscheinlichkeit ≈ 95 % X2 ≤ 46
mit Wahrscheinlichkeit ≈ 99 % X2 ≤ 52.
Auf Abhängigkeiten zwischen aufeinanderfolgenden Additions-
einheiten würden auch Abweichungen von den theoretischen Werten
der Statistiken T3K hingewiesen.
Die Verteilung der Größen t3K wurde in [4] untersucht.
Es gilt
Mt3K = 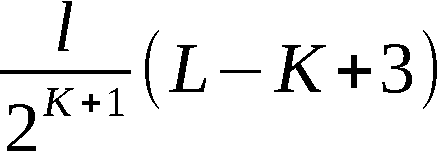 , K = 1,L-1
Mt3L =
, K = 1,L-1
Mt3L = 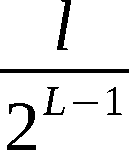 , K = 1,L-1
Da T3K laut Definition eine Summe von Zufallsgrößen t3k
darstellt, folgt hieraus
MT3K =
, K = 1,L-1
Da T3K laut Definition eine Summe von Zufallsgrößen t3k
darstellt, folgt hieraus
MT3K =  , K = 1,L-1
MT3L =
, K = 1,L-1
MT3L =  Man kann t30 als Summe zufälliger Größen betrachten:
t30 = t3,K+1 + t30 = t3,K+2 + … + t30 = t3,L
Dann erhalten wir
Mt30 =
Man kann t30 als Summe zufälliger Größen betrachten:
t30 = t3,K+1 + t30 = t3,K+2 + … + t30 = t3,L
Dann erhalten wir
Mt30 = 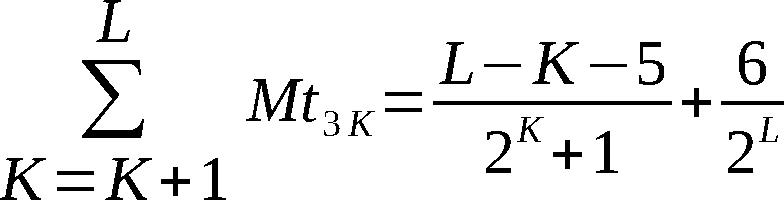 Hieraus folgt
MT30 =
Hieraus folgt
MT30 =  Wir bilden die Größe
Wir bilden die Größe
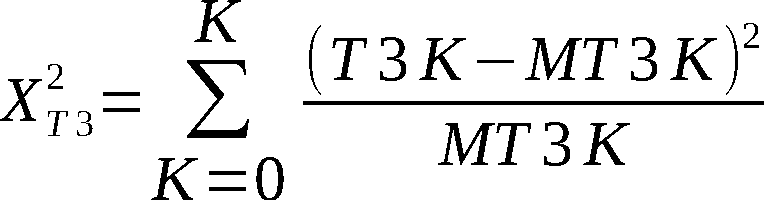 Es wird erwartet, daß sie für N → ∞ gegen die X2-Verteilung
Mit K Freiheitsgraden strebt. Man muß einen geeigneten Wert
für K festlegen.
Für die Anzahl aller Serien t4 erhalten wir aus [4]
Mt4 =
Es wird erwartet, daß sie für N → ∞ gegen die X2-Verteilung
Mit K Freiheitsgraden strebt. Man muß einen geeigneten Wert
für K festlegen.
Für die Anzahl aller Serien t4 erhalten wir aus [4]
Mt4 = 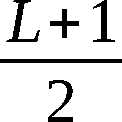 , Dt4 =
, Dt4 =  ;
für L → ∞ nähert sich die Verteilung t4 der Normalverteilung.
Wenn wir die unabhängigen zufälligen Größen aufsummieren,
erhalten wir
MT4 =
;
für L → ∞ nähert sich die Verteilung t4 der Normalverteilung.
Wenn wir die unabhängigen zufälligen Größen aufsummieren,
erhalten wir
MT4 =  , DT4 =
, DT4 = 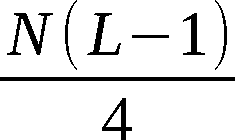 .
Entsprechend muß sich mit Wahrscheinlichkeit 68 %, 96 %, 99,7 %
der beobachtete Wert T4 in dem Intervall
.
Entsprechend muß sich mit Wahrscheinlichkeit 68 %, 96 %, 99,7 %
der beobachtete Wert T4 in dem Intervall
 , δ = 1,2,3
befinden.
Wir betrachten t5. Wenn man A47 und das ihr entsprechende F als
voneinander unabhängig vorausgesetzt, so sind die zufälligen
Größen t1(A47) und t1(F) unabhängig. Wir haben
P[t1(A47) = x] =
, δ = 1,2,3
befinden.
Wir betrachten t5. Wenn man A47 und das ihr entsprechende F als
voneinander unabhängig vorausgesetzt, so sind die zufälligen
Größen t1(A47) und t1(F) unabhängig. Wir haben
P[t1(A47) = x] =  , x = 0,47,
P[t1(F) = x] =
, x = 0,47,
P[t1(F) = x] =  , x = 0,52.
Wenn man bezeichnet c =
, x = 0,52.
Wenn man bezeichnet c =  ≈ 0,1101, so ist
P[t1(A47) ≤ 23] = p[t1(A47) ≥ 24] = 1/2,
p[t1(F) ≤ 25] = p[t1(F) ≥ 27] = 1/2 * c/2,
p[t1(F) ≥ 26] = p[t1(F) = 26]+p[t1(F) ≥ 27] = 1/2 + c/2.
Wenn man die Unabhängigkeit von A47 und F ausnutzt, so folgt
P(t5 = 0) = p(t5 = 2) = (1 - c)/4,
P(t5 = 1) = p(t5 = 3) = (1 + c)/4.
Für NT5K erhalten wir die Binomialverteilung
P(NT5K = x) =
≈ 0,1101, so ist
P[t1(A47) ≤ 23] = p[t1(A47) ≥ 24] = 1/2,
p[t1(F) ≤ 25] = p[t1(F) ≥ 27] = 1/2 * c/2,
p[t1(F) ≥ 26] = p[t1(F) = 26]+p[t1(F) ≥ 27] = 1/2 + c/2.
Wenn man die Unabhängigkeit von A47 und F ausnutzt, so folgt
P(t5 = 0) = p(t5 = 2) = (1 - c)/4,
P(t5 = 1) = p(t5 = 3) = (1 + c)/4.
Für NT5K erhalten wir die Binomialverteilung
P(NT5K = x) = 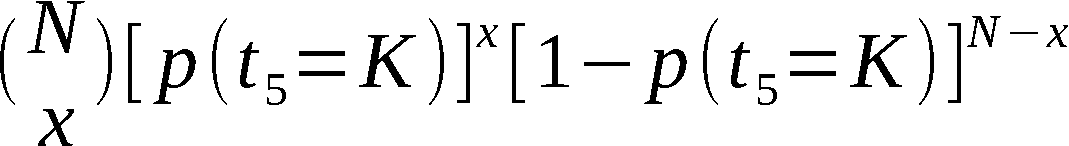 , x = 0,N, K = 0,3.
Folglich ist
MT5K = p(t5 = K),
DT5K =
, x = 0,N, K = 0,3.
Folglich ist
MT5K = p(t5 = K),
DT5K = 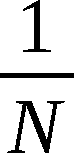 p(t5 = K)*[1-p(t5 = K)].
Die Zahlenwerte sind:
MT50 = MT52 = 0,222 MT51 = MT53 = 0,278
DT50 = DT52 =
p(t5 = K)*[1-p(t5 = K)].
Die Zahlenwerte sind:
MT50 = MT52 = 0,222 MT51 = MT53 = 0,278
DT50 = DT52 =  * 0,17 DT51 = DT53 =
* 0,17 DT51 = DT53 =  * 0,20
Der beobachtete Wert T5K muß sich mit Wahrscheinlichkeit 68 %
oder 96 % oder 99,7 % im Inervall
MT5K ±
* 0,20
Der beobachtete Wert T5K muß sich mit Wahrscheinlichkeit 68 %
oder 96 % oder 99,7 % im Inervall
MT5K ±  ; δ = 1, 2, 3
befinden. Abweichungen würden auf Abhängigkeiten zwischen A47
und F hinweisen. Eine solche Abhängigkeit kännte für die Dekryptierung
(Ordnung der Additionsreihen nach Wahrscheinlichkeit) ausgenutzt
werden, da F dem Dekrypteur bekannt ist.
Man Muß auch fordern, daß sich Abhängigkeiten zwischen ver-
schienen F nicht in den Additionsreihen widerspiegeln. Mit
diesem Ziel wird T6K untersucht.
Es muß gelten
P(t6 = K) = 1/4, K = 0,3,
Folglich ist
P(NT6K = x) =
; δ = 1, 2, 3
befinden. Abweichungen würden auf Abhängigkeiten zwischen A47
und F hinweisen. Eine solche Abhängigkeit kännte für die Dekryptierung
(Ordnung der Additionsreihen nach Wahrscheinlichkeit) ausgenutzt
werden, da F dem Dekrypteur bekannt ist.
Man Muß auch fordern, daß sich Abhängigkeiten zwischen ver-
schienen F nicht in den Additionsreihen widerspiegeln. Mit
diesem Ziel wird T6K untersucht.
Es muß gelten
P(t6 = K) = 1/4, K = 0,3,
Folglich ist
P(NT6K = x) = 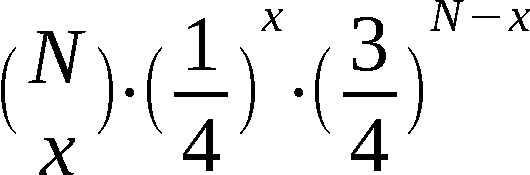 , x = 0,N, K = 0,3.
und deshalb ist
MT6K = 1/4, DT6K =
, x = 0,N, K = 0,3.
und deshalb ist
MT6K = 1/4, DT6K =  * 3/16, K = 0,3.
Der beobachtete Wert T6K muß sich mit Wahrscheinlichkeit
68 %, 96 %, 99,7% im Intervall
* 3/16, K = 0,3.
Der beobachtete Wert T6K muß sich mit Wahrscheinlichkeit
68 %, 96 %, 99,7% im Intervall  , δ = 1, 2, 3
befinden.
3.7.4. Beobachtete Resultate
Es wurden 32 Schlüssel untersucht; drunter einige
reguläre, z. B. S0 = ((0,0),(0,0), …, (0,0)) ∈
, δ = 1, 2, 3
befinden.
3.7.4. Beobachtete Resultate
Es wurden 32 Schlüssel untersucht; drunter einige
reguläre, z. B. S0 = ((0,0),(0,0), …, (0,0)) ∈  Entweder bzgl. der Varianten A + C + D + E oder bzgl.
der Variante B. Die Gesamtzahl der Additionsreihen beträgt
für A - 15220, für B - 32 (der Länge L = 10 000).
In allen Fällen gilt α = 1,
U0 = (000 000 011 011 111 111 100 000 000).
Die Resultate bzgl. der Varianten A + C + D + E siehe
Tabelle I. Hier bedeutet z. B. δT1 = +2, daß der
beobachtete Wert T1 im Intervall
Entweder bzgl. der Varianten A + C + D + E oder bzgl.
der Variante B. Die Gesamtzahl der Additionsreihen beträgt
für A - 15220, für B - 32 (der Länge L = 10 000).
In allen Fällen gilt α = 1,
U0 = (000 000 011 011 111 111 100 000 000).
Die Resultate bzgl. der Varianten A + C + D + E siehe
Tabelle I. Hier bedeutet z. B. δT1 = +2, daß der
beobachtete Wert T1 im Intervall
 liegt.
Kmax bezeichnet den Wert K, für den max T2K erreicht
wird, Kmin - analog.
Die Abweichung von der Gleichverteilung bzgl. Kmax
und Kmin ist dadurch zu erklären, daß die Voraussetzung
in Punkt 3.7.3. über die Unabhängigkeit aufeinanderfolgender
Polygramme nicht völlig korrekt ist.
Der Wert K wurde so gewählt, daß gilt MT3K ≈ 5.
Für N = 1000 ist K = 12, für die restlichen N-Werte ist
K = 14.
Die Resultate bzgl. der Variante B siehe Tabelle II, hier ist
überall K = 10.
Folglich: Die beobachteten Resultate unterstützen die
Hypothese, daß die Additionsreihen die statistischen Eigen-
schaften zufälliger, gleichverteilter, voneinander und von
F unabhängiger Folgen besitzen.
Bemerkung: In dem Dokument
liegt.
Kmax bezeichnet den Wert K, für den max T2K erreicht
wird, Kmin - analog.
Die Abweichung von der Gleichverteilung bzgl. Kmax
und Kmin ist dadurch zu erklären, daß die Voraussetzung
in Punkt 3.7.3. über die Unabhängigkeit aufeinanderfolgender
Polygramme nicht völlig korrekt ist.
Der Wert K wurde so gewählt, daß gilt MT3K ≈ 5.
Für N = 1000 ist K = 12, für die restlichen N-Werte ist
K = 14.
Die Resultate bzgl. der Variante B siehe Tabelle II, hier ist
überall K = 10.
Folglich: Die beobachteten Resultate unterstützen die
Hypothese, daß die Additionsreihen die statistischen Eigen-
schaften zufälliger, gleichverteilter, voneinander und von
F unabhängiger Folgen besitzen.
Bemerkung: In dem Dokument Erste Ergebnisse statistischer
Untersuchungen der Additionsreihe
, GVS 020-623/73, müssen
auf den Seiten 2 und 6 die Werte
 , T2 (1), T2 (2), T2 (3) und
, T2 (1), T2 (2), T2 (3) und 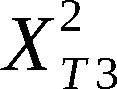 durch die in Tabelle I, N0 29 (S. 2) und N0 30 (S. 6)
angegebenen Werte ersetzt werden. Außerdem muß der Buchstabe
L durch K und M durch L ersetzt werden.
durch die in Tabelle I, N0 29 (S. 2) und N0 30 (S. 6)
angegebenen Werte ersetzt werden. Außerdem muß der Buchstabe
L durch K und M durch L ersetzt werden.
| TAБЛИЦA I |
|---|
| Tabelle I |
|---|
| N0 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 29 | 30 | 31 | 32 |
|---|
| N | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1500 | 720 | 1900 | 4100 |
| T1 | 23,515 | 23,519 | 23,454 | 23,48 | 23,446 | 23,549 | 23,45 | 23,462 | 23,765 | 23,539 | 23,527 |
| δT1(A) | +1 | +1 | -1 | -1 | -1 | +1 | -1 | -1 | +3 | +1 | +1 |
| kmax | 00 | 09 | 31 | 21 | 10 | 28 | 19 | 21 | 29 | 00 | 18/31 |
| kmin | 18 | 23 | 07 | 31 | 23 | 20 | 10 | 25 | 06 | 02 | 00 |
| T2(1) | 24 | 28 | 22 | 24 | 21 | 25 | 19 | 25 | 18 | 27 | 20 |
| T2(2) | 6 | 4 | 10 | 7 | 9 | 7 | 12 | 5 | 13 | 4 | 11 |
| T2(3) | 2 | 0 | 0 | 1 | 2 | 0 | 1 | 2 | 1 | 1 | 1 |
 | 27 | 15 | 22 | 19 | 31,2 | 15 | 32 | 22,5 | 40,3 | 17,1 | 36,9 |
| T30 | 4 | 4 | 3 | 1 | 5 | 2 | 1 | 0 | 2 | 5 | 4 |
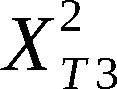 | 12,77 | 4,45 | 8,97 | 11,50 | 12,38 | 7,61 | 19,92 | 8,36 | 10,81 | 18,58 | 12,97 |
| δT4 | -3 | +1 | +1 | +1 | -1 | -1 | -1 | +2 | -1 | +2 | +2 |
| δT1(C) | +1 | -1 | -2 | -2 | -1 | -2 | +1 | +2 | +2 | +1 | -2 |
| δT50 | +1 | +2 | +1 | +1 | +1 | +2 | +1 | -1 | -1 | +1 | -1 |
| δT51 | -1 | -1 | +2 | +1 | +1 | -1 | +1 | +1 | -1 | -1 | +1 |
| δT52 | +1 | -2 | -2 | -1 | -2 | -1 | +1 | -2 | +1 | +1 | -1 |
| δT53 | -1 | -1 | +1 | -1 | +1 | -1 | -2 | +1 | +1 | +1 | +1 |
| δT60 | +1 | +1 | +3 | +1 | +1 | +2 | -2 | -1 | ±0 | -1 | +3 |
| δT61 | -2 | -1 | -1 | +2 | ±0 | +1 | +2 | -2 | -3 | +1 | ±0 |
| δT62 | +1 | -1 | -2 | ±0 | +1 | -1 | -1 | ±0 | +1 | +1 | -2 |
| δT63 | +1 | -1 | +1 | -2 | -1 | -1 | +1 | +2 | +2 | +1 | -2 |
| TAБЛИЦA II |
|---|
| Tabelle II |
|---|
| N0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
|---|
| N | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| T1 | 4976 | 5085,5 | 5018,5 | 5005 | 5006 | 5015,5 | 4964,5 | 4971,5 | 4968,5 | 5003,5 | 4967 | 4953 | 5008 | 4952 | 4908 | 4954 | 4974 | 4945 | 4983 | 5030 | 4966 |
| δT1 | -1 | +3 | +1 | +1 | +1 | +1 | -2 | -1 | -1 | +1 | -1 | -1 | +1 | -1 | -2 | -1 | -1 | -2 | -1 | +1 | -1 |
| kmax | 00 | 31 | 06 | 21 | 00 | 04 | 00 | 31 | 05 | 09 | 00 | 02 | 18 | 00 | 06 | 00/18 | 10 | 12 | 18 | 13/31 | 1/16/20 |
| kmin | 19 | 00/12 | 00 | 28 | 01/16 | 13 | 06 | 19 | 26 | 02 | 17 | 03 | 17 | 14 | 31 | 26 | 31 | 31 | 00 | 10 | 18 |
| T2(1) | 30 | 12 | 25 | 24 | 18 | 19 | 24 | 22 | 24 | 20 | 22 | 17 | 18 | 25 | 22 | 26 | 23 | 26 | 21 | 26 | 21 |
| T2(2) | 1 | 13 | 4 | 7 | 1 | 9 | 7 | 10 | 5 | 10 | 8 | 12 | 11 | 6 | 9 | 5 | 9 | 4 | 10 | 6 | 10 |
| T2(3) | 1 | 3 | 2 | 1 | 2 | 4 | 1 | 0 | 3 | 2 | 1 | 3 | 2 | 1 | 0 | 1 | 0 | 2 | 1 | 0 | 1 |
 | 12,3 | 77,362 | 33,26 | 23,34 | 40,57 | 50,09 | 24,914 | 29,216 | 29,06 | 29,92 | 38,274 | 46,387 | 53,545 | 23,46 | 32,6 | 18,275 | 22,425 | 25,224 | 28,134 | 22,013 | 29753 |
| T30 | 9 | 9 | 5 | 11 | 13 | 7 | 8 | 11 | 13 | 9 | 9 | 4 | 7 | 3 | 6 | 4 | 2 | 3 | 3 | 3 | 4 |
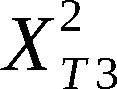 | 12,37 | 14,65 | 7,8 | 8,72 | 4,55 | 8,74 | 14,67 | 13,32 | 4,02 | 9,03 | 22,80 | 14,38 | 10,87 | 8,85 | 10,99 | 5,73 | 9,17 | 9,98 | 7,23 | 6,23 | 5,19 |
| δT4 | -1 | +1 | +2 | +1 | -1 | +2 | -1 | -1 | +1 | -1 | +1 | +2 | -1 | -1 | +1 | -1 | +1 | +1 | +2 | -1 | +1 |
4. Ausführungen zu Kapitel V
4.1. Methoden zur Bestimmung des Schlüssels
4.1.1. Wir betrachten die Komponentenfolge ( )
)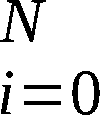 für
festes α ∈ 1,27 und N ≥ 52, für beliebig festes U0 ∈
für
festes α ∈ 1,27 und N ≥ 52, für beliebig festes U0 ∈  in Abhängigkeit von F ∈
in Abhängigkeit von F ∈  .
Dann sind für gegebenes S ∈
.
Dann sind für gegebenes S ∈  für alle 252 Folgen paarweise
verschieden auf Grund der Eigenschaften der Abbildung ϕ.
Legen wir eine gewisse eineindeutige Zuordnung zwischen
der Menge {0,1}52 und der Menge der Zahlen 1,252 fest.
Dann kann man für gegebenes S die Gesamtheit der Komponenten-
folgen als Permutation Π(S) dieser Zahlenmenge betrachten,
indem man (
für alle 252 Folgen paarweise
verschieden auf Grund der Eigenschaften der Abbildung ϕ.
Legen wir eine gewisse eineindeutige Zuordnung zwischen
der Menge {0,1}52 und der Menge der Zahlen 1,252 fest.
Dann kann man für gegebenes S die Gesamtheit der Komponenten-
folgen als Permutation Π(S) dieser Zahlenmenge betrachten,
indem man ( )
) berücksichtigt. Die Eigenschaft Π(S) = Π(S')
für bestimmte S ≠ S' ist gleichbedeutend mit der Äquivalenz
dieser Schlüssel bezüglich der Folge (
berücksichtigt. Die Eigenschaft Π(S) = Π(S')
für bestimmte S ≠ S' ist gleichbedeutend mit der Äquivalenz
dieser Schlüssel bezüglich der Folge ( )
) für festes
U0 ∈
für festes
U0 ∈  .
Für α = 1 folgt aus der Darstellung
(*) u
.
Für α = 1 folgt aus der Darstellung
(*) u = s
= s + fi + s
+ fi + s ∆1 + T1(s
∆1 + T1(s ,U
,U ); i = 1,52
daß für einen gegebenen Platz in der Permutation
Π(d. h. für gegebenes F) 252 * 452 Schlüssel existieren,
für die Π(S) an dieser Stelle übereinstimmen.
Die Aufgabe besteht in der Bestimmung von S, falls Π(S)
teilweise oder vollständig bekannt ist.
Falls Π(S) bekannt ist, dann ist S bis auf äquivalente
(im obigen Sinne) Schlüssel bekannt.
Wenn ein Element der Permutation Π(S) bekannt ist, so sind
2156 Elemente S ∈
); i = 1,52
daß für einen gegebenen Platz in der Permutation
Π(d. h. für gegebenes F) 252 * 452 Schlüssel existieren,
für die Π(S) an dieser Stelle übereinstimmen.
Die Aufgabe besteht in der Bestimmung von S, falls Π(S)
teilweise oder vollständig bekannt ist.
Falls Π(S) bekannt ist, dann ist S bis auf äquivalente
(im obigen Sinne) Schlüssel bekannt.
Wenn ein Element der Permutation Π(S) bekannt ist, so sind
2156 Elemente S ∈  bekannt, die an gegebener Stelle in Π
das bekannte Element besitzen.
Wieviel Elemente von Π(S) müssen bekannt sein, um S
eindeutig bestimmen zu können?
Seien zwei Elemente von Π(S) bekannt. Wir betrachten und
vergleichen die Gleichungen, die (*) entsprechen,
für S ∈ und S' ∈
bekannt, die an gegebener Stelle in Π
das bekannte Element besitzen.
Wieviel Elemente von Π(S) müssen bekannt sein, um S
eindeutig bestimmen zu können?
Seien zwei Elemente von Π(S) bekannt. Wir betrachten und
vergleichen die Gleichungen, die (*) entsprechen,
für S ∈ und S' ∈  , sowie für die Elemente F1 ∈
, sowie für die Elemente F1 ∈  und F2 ∈
und F2 ∈  für die Elemente von Π(S) bekannt sind. Die gleichzeitige
Erfüllung aller dieser Gleichungen ist dann wenig wahr-
scheinlich, wenn sich die Komponenten von F1 und F2 bereits
für kleine i unterscheiden.
Deshalb ist in der Regel damit zu rechnen, daß sich aus der
Kenntnis zweier Elemente von Π(S) der Schlüssel schon eindeutig
ergibt. Die Nichteindeutigkeit ist dann wahrscheinlich, wenn
sich F1 und F2 unwesentlich und nur in den letzten Stellen
(für i ≈ 52) unterscheiden.
Das Problem der Bestimmung von S, ausgehend von den
Komponentenfolgen für verschiedene F wurde bereits in
[1; V, §1, 4.3] betrachtet.
Die dort und hier erhaltenen Resultate ergänzen einander.
Bei der praktischen Bestimmung ergibt sich S auf dem in [1]
gezeigten Weg.
Um den Realen Wert dieser Methode einzuschätzen, muß man
berücksichtigen, daß der Dekrypteur nicht schwerer die
Klartexte oder den Schlüssel bekommt, als die Kompo-
nentenfolge.
4.1.2. Betrachten wir einen festen Langzeitschlüssel (P,R,α,U0).
Wir zerlegen
für die Elemente von Π(S) bekannt sind. Die gleichzeitige
Erfüllung aller dieser Gleichungen ist dann wenig wahr-
scheinlich, wenn sich die Komponenten von F1 und F2 bereits
für kleine i unterscheiden.
Deshalb ist in der Regel damit zu rechnen, daß sich aus der
Kenntnis zweier Elemente von Π(S) der Schlüssel schon eindeutig
ergibt. Die Nichteindeutigkeit ist dann wahrscheinlich, wenn
sich F1 und F2 unwesentlich und nur in den letzten Stellen
(für i ≈ 52) unterscheiden.
Das Problem der Bestimmung von S, ausgehend von den
Komponentenfolgen für verschiedene F wurde bereits in
[1; V, §1, 4.3] betrachtet.
Die dort und hier erhaltenen Resultate ergänzen einander.
Bei der praktischen Bestimmung ergibt sich S auf dem in [1]
gezeigten Weg.
Um den Realen Wert dieser Methode einzuschätzen, muß man
berücksichtigen, daß der Dekrypteur nicht schwerer die
Klartexte oder den Schlüssel bekommt, als die Kompo-
nentenfolge.
4.1.2. Betrachten wir einen festen Langzeitschlüssel (P,R,α,U0).
Wir zerlegen  in Äquivalenzklassen Ki, i = 1,247
in Abhängigkeit von F ∈
in Äquivalenzklassen Ki, i = 1,247
in Abhängigkeit von F ∈  , wobei in einer Klasse alle S ∈
, wobei in einer Klasse alle S ∈  enthalten seinen, die bei diesem F die gleiche Additions-
reihe AL mit L = 47 erzeugen.
Wir setzen bekannte Additionsreihen A1, A2, …, An
voraus, die durch paarweise verschiedene (bekannte)
F1, F2, …, Fn und ein und dem selben (unbekannten) S
erzeugt sind.
Dann ist
S ∈
enthalten seinen, die bei diesem F die gleiche Additions-
reihe AL mit L = 47 erzeugen.
Wir setzen bekannte Additionsreihen A1, A2, …, An
voraus, die durch paarweise verschiedene (bekannte)
F1, F2, …, Fn und ein und dem selben (unbekannten) S
erzeugt sind.
Dann ist
S ∈  .
Indem man die Zerlegung von
.
Indem man die Zerlegung von  in Klassen ausnutzt, kann
man S bei hinreichend großem n als eindeutig bestimmbar
ansehen.
Im Mittel ist |Ki| = 2208-47 = 2161, obgleich starke
Abweichungen möglich scheinen (denkbar ist sogar, daß
einige Klassen leer sind).
Wenn die erste Additionsreihe A1 und F1 bekannt ist,
kann man die Zahl der möglichen Schlüssel im Mittel von
2208 auf 2161 verringern. Kennt man die zweite Folge
A2 und F2, kann man eine andere Klasse bestimmen.
Der Durchschnitt beider Klassen enthält im Mittel
2208-2*47 = 2114 Elemente.
Weiter fortgesetzt verbleiben nach der Auswertung von
drei Additionsreihen 267 und nach der Auswertung von
vier Additionsreihen 220 Schlüssel im Mittel.
Im Mittel mit der fünften Additionsreihe wird der Schlüs-
sel eindeutig bestimmt, und die Aufgabe ist gelöst.
Kann man diese Methode in der Praxis anwenden?
Im ersten Schritt muß der Durchschnitt der Klassen gefunden
werden, die F1 und F2 entsprechen. Dazu muß jedes von
2161 Elementen der ersten Klasse verglichen werden. Diese Zahl
ist im Mittel nicht kleiner als 2161, sogar wenn die
Elemente in der Menge
in Klassen ausnutzt, kann
man S bei hinreichend großem n als eindeutig bestimmbar
ansehen.
Im Mittel ist |Ki| = 2208-47 = 2161, obgleich starke
Abweichungen möglich scheinen (denkbar ist sogar, daß
einige Klassen leer sind).
Wenn die erste Additionsreihe A1 und F1 bekannt ist,
kann man die Zahl der möglichen Schlüssel im Mittel von
2208 auf 2161 verringern. Kennt man die zweite Folge
A2 und F2, kann man eine andere Klasse bestimmen.
Der Durchschnitt beider Klassen enthält im Mittel
2208-2*47 = 2114 Elemente.
Weiter fortgesetzt verbleiben nach der Auswertung von
drei Additionsreihen 267 und nach der Auswertung von
vier Additionsreihen 220 Schlüssel im Mittel.
Im Mittel mit der fünften Additionsreihe wird der Schlüs-
sel eindeutig bestimmt, und die Aufgabe ist gelöst.
Kann man diese Methode in der Praxis anwenden?
Im ersten Schritt muß der Durchschnitt der Klassen gefunden
werden, die F1 und F2 entsprechen. Dazu muß jedes von
2161 Elementen der ersten Klasse verglichen werden. Diese Zahl
ist im Mittel nicht kleiner als 2161, sogar wenn die
Elemente in der Menge  wohl geordnet sind, betrachteten
wir beispielsweise
wohl geordnet sind, betrachteten
wir beispielsweise  als die Zahlenmenge {1,2, …, 2208},
und daher ist dieser Weg in der Praxis untauglich.
Die Anzahl der Elementaroperationen kann daher nicht zu
einer hinreichend kleinen Zahl absinken. Die betrachtete
Methode erfordert außerdem die Berechnung und Speicherung
von 252 Zerlegungen der Menge
als die Zahlenmenge {1,2, …, 2208},
und daher ist dieser Weg in der Praxis untauglich.
Die Anzahl der Elementaroperationen kann daher nicht zu
einer hinreichend kleinen Zahl absinken. Die betrachtete
Methode erfordert außerdem die Berechnung und Speicherung
von 252 Zerlegungen der Menge  in Klassen, was in der
Praxis unmöglich ist. Folglich vereinfacht diese Methode
nicht die Lösung des Problems der Rekonstruktion des
Schlüssels.
4.2. Über Dekryptierbarkeit ohne Rekonstruktion des Schlüssels
4.2.1. Wir betrachten die Aufgabe der unmittelbaren Erarbeitung
einer Information aus Geheimtexten, ohne den Schlüssel
selber zu rekonstruieren. Wir setzen voraus, daß alle
Additionsreihen zufällige, gleichwahrscheinliche und
voneinander unabhängige Folgen der Länge 47 sind. Das heißt,
die Situation ist eben die wie bei einer Chiffrierabbildung
mit garantierter Sicherheit. (Dies ist die einzig mögliche
Voraussetzung, da es keinerlei Hinweise darauf gibt, wie man
die vorhandenen Abhängigkeiten zwischen den Additionsreihen
ausnutzen könnte)
4.2.2. Zuerst betrachten wir identische Additionsreihen.
Die Wahrscheinlichkeit dafür, daß zwei gegebene Addi-
tionsreihen identisch sind, ist gleich 2-47.
Wir bezeichnen mit G = (g1, g2, …, g47)
den Grundtext und mit A = (a1, a2, …, a47)
die Additionsreihe. Dann wird der Geheimtext C = (c1, c2, …, c47)
nach der Formel C = G + A = (g1 + a1, g2 + 12, …, g47 + a47)
gebildet.
Wir formulieren notwendige Bedingungen dafür, daß ein
gegebenes Paar von Geheimtexten (C1, C2) ein und
dieselbe Additionsreihe hat.
(N1) C
in Klassen, was in der
Praxis unmöglich ist. Folglich vereinfacht diese Methode
nicht die Lösung des Problems der Rekonstruktion des
Schlüssels.
4.2. Über Dekryptierbarkeit ohne Rekonstruktion des Schlüssels
4.2.1. Wir betrachten die Aufgabe der unmittelbaren Erarbeitung
einer Information aus Geheimtexten, ohne den Schlüssel
selber zu rekonstruieren. Wir setzen voraus, daß alle
Additionsreihen zufällige, gleichwahrscheinliche und
voneinander unabhängige Folgen der Länge 47 sind. Das heißt,
die Situation ist eben die wie bei einer Chiffrierabbildung
mit garantierter Sicherheit. (Dies ist die einzig mögliche
Voraussetzung, da es keinerlei Hinweise darauf gibt, wie man
die vorhandenen Abhängigkeiten zwischen den Additionsreihen
ausnutzen könnte)
4.2.2. Zuerst betrachten wir identische Additionsreihen.
Die Wahrscheinlichkeit dafür, daß zwei gegebene Addi-
tionsreihen identisch sind, ist gleich 2-47.
Wir bezeichnen mit G = (g1, g2, …, g47)
den Grundtext und mit A = (a1, a2, …, a47)
die Additionsreihe. Dann wird der Geheimtext C = (c1, c2, …, c47)
nach der Formel C = G + A = (g1 + a1, g2 + 12, …, g47 + a47)
gebildet.
Wir formulieren notwendige Bedingungen dafür, daß ein
gegebenes Paar von Geheimtexten (C1, C2) ein und
dieselbe Additionsreihe hat.
(N1) C + C
+ C = 0, für i = 3,6
Das folgt daraus, daß die Elemente gi, i = 3,7,
bei allen Klartexten konstant sind, [1; I, §2];
mit Ausnahme von Blendtexten, die uns nicht interessieren.
(N2)
= 0, für i = 3,6
Das folgt daraus, daß die Elemente gi, i = 3,7,
bei allen Klartexten konstant sind, [1; I, §2];
mit Ausnahme von Blendtexten, die uns nicht interessieren.
(N2) 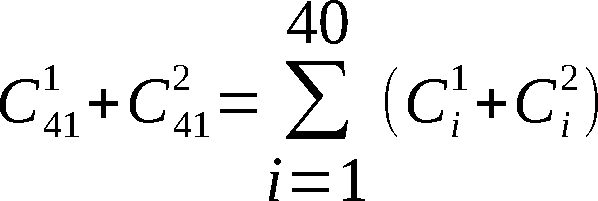 Das folgt daraus, daß das Element g41 (Parität) eindeutig
durch die Summe
Das folgt daraus, daß das Element g41 (Parität) eindeutig
durch die Summe 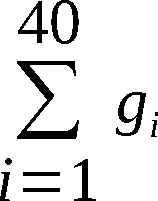 bestimmt ist.
Aus den Eigenschaften der Codesicherung I folgt (N3)
Die Summe C1 + C2 ist ein Codevektor.
Wenn man berücksichtigt, daß man aus dem Blendtext keinerlei
Informationen erhalten kann, so können nur solche Texte
interessieren, die keine Blendtexte sind. Für sie nimmt
g2 einen festen Wert an. Folglich:
(N4) C
bestimmt ist.
Aus den Eigenschaften der Codesicherung I folgt (N3)
Die Summe C1 + C2 ist ein Codevektor.
Wenn man berücksichtigt, daß man aus dem Blendtext keinerlei
Informationen erhalten kann, so können nur solche Texte
interessieren, die keine Blendtexte sind. Für sie nimmt
g2 einen festen Wert an. Folglich:
(N4) C + C
+ C = 0
Wir berechnen jetzt die Zahl der Paare (C1, C2),
die (N1) - (N4) genügen, wobei wir die entsprechenden
A1 und A2 als unabhängig voraussetzen und Blendtexte
nicht berücksichtigen.
Dann genügt das gegebene Paar (C1, C2) (N1) mit
(N4) - 2-1. Folglich sind unter n Paaren von Geheimtexten
(ohne Blendtexte) im Mittel n * 2-12 Paare, die (N1) - (N4)
genügen.
Der Dekrypteur habe 224 ≈ 16 000 000 Geheimtextblöcke
ohne Blendtexte zur Verfügung. Sie bilden (
= 0
Wir berechnen jetzt die Zahl der Paare (C1, C2),
die (N1) - (N4) genügen, wobei wir die entsprechenden
A1 und A2 als unabhängig voraussetzen und Blendtexte
nicht berücksichtigen.
Dann genügt das gegebene Paar (C1, C2) (N1) mit
(N4) - 2-1. Folglich sind unter n Paaren von Geheimtexten
(ohne Blendtexte) im Mittel n * 2-12 Paare, die (N1) - (N4)
genügen.
Der Dekrypteur habe 224 ≈ 16 000 000 Geheimtextblöcke
ohne Blendtexte zur Verfügung. Sie bilden (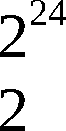 ) ≈ 247 Paare,
unter denen im Mittel ein Paar mit ein und derselben
Additionsreihe ist. Wenn man die Kriterien (N1) - (N4)
anwendet, verringert sich die Zahl der Paare, die man für
die weitere Verarbeitung speichern muß auf 235 ≈ 3 * 1010.
Da es nicht gelingt andere notwendige oder gar hinreichende
Kriterien zu finden, folgt hieraus klar, daß es faktisch
nicht gelingt, die Paare (C1, C2) zu finden, die ein und
dieselbe Additionsreihe besitzen.
4.2.3. Wir setzen voraus, daß der Dekrypteur trotz allem weiß
(oder mit hinreichend großer Bestimmtheit annimmt), daß
das gegebene Paar ein und dieselbe Additionsreihe besitzt.
Dann kann man ausnutzen, daß die Frequenz und die Zusatz-
information im Code BCD 2421 dargestellt werden.
Das bedeutet, daß an den Stellen
G(i) = g7+4i g8+4i g9+4i g10+4i i = 0,7
nur 10 von 16 möglichen Werten aus {1,0}4 stehen können.
Für A1 = A2 kann man schreiben
G2 = G1 + C1 + C2.
Wenn G
) ≈ 247 Paare,
unter denen im Mittel ein Paar mit ein und derselben
Additionsreihe ist. Wenn man die Kriterien (N1) - (N4)
anwendet, verringert sich die Zahl der Paare, die man für
die weitere Verarbeitung speichern muß auf 235 ≈ 3 * 1010.
Da es nicht gelingt andere notwendige oder gar hinreichende
Kriterien zu finden, folgt hieraus klar, daß es faktisch
nicht gelingt, die Paare (C1, C2) zu finden, die ein und
dieselbe Additionsreihe besitzen.
4.2.3. Wir setzen voraus, daß der Dekrypteur trotz allem weiß
(oder mit hinreichend großer Bestimmtheit annimmt), daß
das gegebene Paar ein und dieselbe Additionsreihe besitzt.
Dann kann man ausnutzen, daß die Frequenz und die Zusatz-
information im Code BCD 2421 dargestellt werden.
Das bedeutet, daß an den Stellen
G(i) = g7+4i g8+4i g9+4i g10+4i i = 0,7
nur 10 von 16 möglichen Werten aus {1,0}4 stehen können.
Für A1 = A2 kann man schreiben
G2 = G1 + C1 + C2.
Wenn G 10 BCD-Werte durchläuft, so nimmt nicht in
allen Fällen G
10 BCD-Werte durchläuft, so nimmt nicht in
allen Fällen G auch BCD-Werte an, im Mittel nur in ≈ 2/3
aller Fälle. In einem beliebigen Fall, jedoch ergeben sich
zumindest einige vereinbare Paare (G
auch BCD-Werte an, im Mittel nur in ≈ 2/3
aller Fälle. In einem beliebigen Fall, jedoch ergeben sich
zumindest einige vereinbare Paare (G ,G
,G ).
Wenn der Dekrypteur das Nachrichtennetz so gut kennt, daß
er die Klartexte nach Wahrscheinlichkeit ordnen kann
(diese Annahme ist genügend realistisch) so kann er das
Paar (G1,G2) finden, das mit der größten Wahrscheinlichkeit
(C1,C2) entspricht.
Die Sicherheit der Chiffrierabbildung sinkt damit nicht ab,
weil solche Paare nur mit Wahrscheinlichkeit 2-47 auftreten
und das am meisten wahrscheinliche Paar durchaus nicht
das richtige sein muß.
4.2.4. Wir betrachten den Fall der im gewissen Sinne "nahen"
oder abhängigen Additionsreihen, zum Beispiel
A2 + A2 = (1, 1, …, 1) oder (0, 0, …, 1, 0, …, 0)
oder a
).
Wenn der Dekrypteur das Nachrichtennetz so gut kennt, daß
er die Klartexte nach Wahrscheinlichkeit ordnen kann
(diese Annahme ist genügend realistisch) so kann er das
Paar (G1,G2) finden, das mit der größten Wahrscheinlichkeit
(C1,C2) entspricht.
Die Sicherheit der Chiffrierabbildung sinkt damit nicht ab,
weil solche Paare nur mit Wahrscheinlichkeit 2-47 auftreten
und das am meisten wahrscheinliche Paar durchaus nicht
das richtige sein muß.
4.2.4. Wir betrachten den Fall der im gewissen Sinne "nahen"
oder abhängigen Additionsreihen, zum Beispiel
A2 + A2 = (1, 1, …, 1) oder (0, 0, …, 1, 0, …, 0)
oder a = a
= a für festes K und gewisse i.
Man kann notwendige Kriterien für die Erfüllung solcher
Beziehungen finden. Aber aufgrund der geringen Wahrschein-
lichkeit dieser Ereignisse und der geringen Effektivität
dieser Kriterien gelingt es faktisch weder solcher Paare
zu finden, noch sie auszunutzen.
4.2.5. Folglich: Das Dekryptieren ohne Rekonstruktion des
Schlüssels ist in der Praxis unmöglich.
4.3. Der Einfluß der Blendnachrichten auf die kryptologischen
Eigenschaften des Systems OPERATION
Bei störungsfreier Arbeit der Technik und ihrer vorschrifts-
mäßigen Bedienung unterscheiden sich die Blendnachrichten
auf dem Kanal in keiner Weise von operativen Nachrichten.
Von 241 theoretisch möglichen Klartextblöcken können
240 als Blendklartexte auftreten.
Die Eigenschaften des Polynoms x41 + x38 + 1, das der
rekurrenten Folge entspricht, die die Blendblöcke bildet,
garantieren, daß alle 240 Blöcke in der Praxis etwa gleich
oft auftreten werden. Unmittelbar aufeinanderfolgende
Blöcke sind durch die rekurrente Gleichung verbunden.
Diese Verbindung auszunutzen ist jedoch für en Dekrypteur
nicht einfacher, als die Eigenschaften der operativen
Klartexte auszunutzen.
Da die Übermittlung der Blendnachrichten durch Tastendruck
verwirklicht wird, beeinflussen subjektive Faktoren
wesentlich die Effektivität der Blendnachrichten. Man muß
genaue Vorschriften für ihre Verwendung formulieren.
Technische Mängel bei der Erarbeitung und Übermittlung von
Blendnachrichten können durch die Wirkung der Blockierungen
nicht zu einer Verringerung der kryptologischen Sicherheit
führen.
5. Zusammenfassung
5.1. Zusammenfassung der Resultate
Die Untersuchung der zyklischen Struktur der Abbildung
ϕ(0,0,0) zeigt, daß bei der Wahl des Langzeitschlüssels
(P,R) = (P0,R0) und U0 entsprechend den Hinweisen in
[1; Zusammenfassung, 3.2] die Zustandsklasse nicht weniger
als 92,2 * 106 Elemente enthält.
Für (P0,R0) ist die in [1] erarbeitete hinreichende
Bedingung für die Nichtexistenz äquivalenter Schlüssel
bzgl. UN erfüllt.
Die experimentelle Untersuchung unterstützt die Hypothese,
daß die Additionsreihen die statistischen Eigenschaften
zufälliger, gleichverteilter unabhängiger Folgen besitzen.
Die Suche nach weiteren Methoden der Bestimmung des Schlüssels
und die Untersuchung der Aufgabe des Lesens der Chiffrier-
abbildung ohne den Schlüssel zu bestimmen zeigen, daß die
kryptologische Sicherheit der Chiffrierabbildung den For-
derungen genügt.
Das System der Erarbeitung und Verwendung von Blendnachrichten
genügt den Forderungen.
5.2. Wichtige, ungelöste Probleme
- Äquivalente Schlüssel bzgl. der Additionsreihe
- Analytische Abhängigkeit der Additionseinheiten
von den Anfangswerten
- Periode der Additionsreihe
- Theoretische Begründung der statistischen Eigenschaften
der Additionsreihe
- Bilden alle Zustände eine einzige Klasse?
5.3. Richtungen der weiteren Untersuchung
5.3.1. Untersuchung der Funktion h
für festes K und gewisse i.
Man kann notwendige Kriterien für die Erfüllung solcher
Beziehungen finden. Aber aufgrund der geringen Wahrschein-
lichkeit dieser Ereignisse und der geringen Effektivität
dieser Kriterien gelingt es faktisch weder solcher Paare
zu finden, noch sie auszunutzen.
4.2.5. Folglich: Das Dekryptieren ohne Rekonstruktion des
Schlüssels ist in der Praxis unmöglich.
4.3. Der Einfluß der Blendnachrichten auf die kryptologischen
Eigenschaften des Systems OPERATION
Bei störungsfreier Arbeit der Technik und ihrer vorschrifts-
mäßigen Bedienung unterscheiden sich die Blendnachrichten
auf dem Kanal in keiner Weise von operativen Nachrichten.
Von 241 theoretisch möglichen Klartextblöcken können
240 als Blendklartexte auftreten.
Die Eigenschaften des Polynoms x41 + x38 + 1, das der
rekurrenten Folge entspricht, die die Blendblöcke bildet,
garantieren, daß alle 240 Blöcke in der Praxis etwa gleich
oft auftreten werden. Unmittelbar aufeinanderfolgende
Blöcke sind durch die rekurrente Gleichung verbunden.
Diese Verbindung auszunutzen ist jedoch für en Dekrypteur
nicht einfacher, als die Eigenschaften der operativen
Klartexte auszunutzen.
Da die Übermittlung der Blendnachrichten durch Tastendruck
verwirklicht wird, beeinflussen subjektive Faktoren
wesentlich die Effektivität der Blendnachrichten. Man muß
genaue Vorschriften für ihre Verwendung formulieren.
Technische Mängel bei der Erarbeitung und Übermittlung von
Blendnachrichten können durch die Wirkung der Blockierungen
nicht zu einer Verringerung der kryptologischen Sicherheit
führen.
5. Zusammenfassung
5.1. Zusammenfassung der Resultate
Die Untersuchung der zyklischen Struktur der Abbildung
ϕ(0,0,0) zeigt, daß bei der Wahl des Langzeitschlüssels
(P,R) = (P0,R0) und U0 entsprechend den Hinweisen in
[1; Zusammenfassung, 3.2] die Zustandsklasse nicht weniger
als 92,2 * 106 Elemente enthält.
Für (P0,R0) ist die in [1] erarbeitete hinreichende
Bedingung für die Nichtexistenz äquivalenter Schlüssel
bzgl. UN erfüllt.
Die experimentelle Untersuchung unterstützt die Hypothese,
daß die Additionsreihen die statistischen Eigenschaften
zufälliger, gleichverteilter unabhängiger Folgen besitzen.
Die Suche nach weiteren Methoden der Bestimmung des Schlüssels
und die Untersuchung der Aufgabe des Lesens der Chiffrier-
abbildung ohne den Schlüssel zu bestimmen zeigen, daß die
kryptologische Sicherheit der Chiffrierabbildung den For-
derungen genügt.
Das System der Erarbeitung und Verwendung von Blendnachrichten
genügt den Forderungen.
5.2. Wichtige, ungelöste Probleme
- Äquivalente Schlüssel bzgl. der Additionsreihe
- Analytische Abhängigkeit der Additionseinheiten
von den Anfangswerten
- Periode der Additionsreihe
- Theoretische Begründung der statistischen Eigenschaften
der Additionsreihe
- Bilden alle Zustände eine einzige Klasse?
5.3. Richtungen der weiteren Untersuchung
5.3.1. Untersuchung der Funktion h (siehe Punkt 3.3.
dieser Ergänzung).
5.3.2. Untersuchung vereinfachter Modelle von Chiffrier-
abbildungen
Schlußfolgerungen
Die Schlußfolgerungen der Analyse [1] bleiben gültig.
Krey Helbig
Hauptmann Oberleutnant
Einverstanden Leiter der Unterabteilung
Hübler
Major
Literatur:
[1] Kryptologische Analyse des Chiffrators des Systems
OPERATION, GVS MfS 020 747/73
[2] Die Zyklenstruktur der Abbildung ϕ im Chiffriersystem
des Systems OPERATION, GVS MfS 020 867/73
[3] KENDALL, STUART: Theorie der Verteilung, Übersetzung
aus dem Englischen ins Russische, Moskau 1966
[4] GONTSCHAROW: aus dem Gebiet der Kombinatorik, russisch,
Nachrichten der Akademie der Wissenschaften der UdSSR,
math. Serie, 8 (1944)
(siehe Punkt 3.3.
dieser Ergänzung).
5.3.2. Untersuchung vereinfachter Modelle von Chiffrier-
abbildungen
Schlußfolgerungen
Die Schlußfolgerungen der Analyse [1] bleiben gültig.
Krey Helbig
Hauptmann Oberleutnant
Einverstanden Leiter der Unterabteilung
Hübler
Major
Literatur:
[1] Kryptologische Analyse des Chiffrators des Systems
OPERATION, GVS MfS 020 747/73
[2] Die Zyklenstruktur der Abbildung ϕ im Chiffriersystem
des Systems OPERATION, GVS MfS 020 867/73
[3] KENDALL, STUART: Theorie der Verteilung, Übersetzung
aus dem Englischen ins Russische, Moskau 1966
[4] GONTSCHAROW: aus dem Gebiet der Kombinatorik, russisch,
Nachrichten der Akademie der Wissenschaften der UdSSR,
math. Serie, 8 (1944)
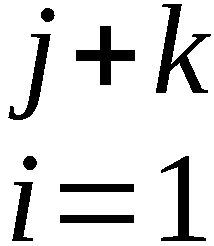 (k > 76) von W = (wi)
(k > 76) von W = (wi) ,
dessen Anfangsabschnitt (wi)
,
dessen Anfangsabschnitt (wi) als Additionsreihe genutzt wird.
3. Prüfung und Blockierung
§2 Das Schlüsselsystem
1. Kurzzeitschlüssel
2. Langzeitschlüssel
3. Reserveschlüssel
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der
kryptologischen Schaltung
2. Festlegung des Schlüsselsystems
3. Grundprinzip der Erzeugung der Folge W
4. Festlegung der Grundstruktur der krypto-
logischen Schaltung II
5. Festlegung der Parameter der kryptolo-
gischen Schaltung II
5.1 Anzahl der internen Arbeitstakte T 350 kHz
pro Übertragungstakt TÜi
5.2 Kurzzeitschlüssel
5.3 Zustandsspeicher U
5.4 Realisierung der Überführungsfunktion
5.5 Verarbeitung von FUi, S1 und S2
5.6 Einstellung des Anfangszustandes U(0)
5.7 Abgriff der Elemente wi von W
§4 Kryptologische Sicherheit im System OPERATION
§5 Änderungsmöglichkeiten der kryptologischen
Schaltung des Chiffrators
1. Allgemeine Aussagen
2. Änderung der Struktur des Zustandsspeichers
3. Änderung der Funktion x
4. Änderung der Festlegung des Anfangszustan-
des U(0)
Kapitel IV Die Untersuchung der Struktur der Chiffierabbildung
Einführung
§1 Die Abbildung ϕ
1. Definition der Abbildung ϕ
2. Bedingungen für die Eineindeutigkeit von ϕ
2.1 Das grundlegende Gleichungssystem
2.2 Notwendige Bedingungen
2.3 Hinreichende Bedingungen
2.4 Die Anzahl der Elemente in PR
3. Fixpunkte
4. Zustandsklassen
4.1 Definition einer Zustandsklasse
4.2 Die Menge {ϕnU}
4.3 Die Mengen {ϕU1 U2} und {ϕ-1ϕU}
5. Der Spezialfall {P0, R0}
§2 Determiniertes Chiffratormodell
1. Definition von Abbildungen
2. Kryptologische Interpretation und elementare
Eigenschaften der Abbildungen
3. Periodizitätseigenschaften
3.1 Periodizität von Folgen
3.2 Die Periode der Folge r
3.3 Die Periode der Folge (Ui)i=0,1,2,…
3.4 Die Periode der Folge (
als Additionsreihe genutzt wird.
3. Prüfung und Blockierung
§2 Das Schlüsselsystem
1. Kurzzeitschlüssel
2. Langzeitschlüssel
3. Reserveschlüssel
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der
kryptologischen Schaltung
2. Festlegung des Schlüsselsystems
3. Grundprinzip der Erzeugung der Folge W
4. Festlegung der Grundstruktur der krypto-
logischen Schaltung II
5. Festlegung der Parameter der kryptolo-
gischen Schaltung II
5.1 Anzahl der internen Arbeitstakte T 350 kHz
pro Übertragungstakt TÜi
5.2 Kurzzeitschlüssel
5.3 Zustandsspeicher U
5.4 Realisierung der Überführungsfunktion
5.5 Verarbeitung von FUi, S1 und S2
5.6 Einstellung des Anfangszustandes U(0)
5.7 Abgriff der Elemente wi von W
§4 Kryptologische Sicherheit im System OPERATION
§5 Änderungsmöglichkeiten der kryptologischen
Schaltung des Chiffrators
1. Allgemeine Aussagen
2. Änderung der Struktur des Zustandsspeichers
3. Änderung der Funktion x
4. Änderung der Festlegung des Anfangszustan-
des U(0)
Kapitel IV Die Untersuchung der Struktur der Chiffierabbildung
Einführung
§1 Die Abbildung ϕ
1. Definition der Abbildung ϕ
2. Bedingungen für die Eineindeutigkeit von ϕ
2.1 Das grundlegende Gleichungssystem
2.2 Notwendige Bedingungen
2.3 Hinreichende Bedingungen
2.4 Die Anzahl der Elemente in PR
3. Fixpunkte
4. Zustandsklassen
4.1 Definition einer Zustandsklasse
4.2 Die Menge {ϕnU}
4.3 Die Mengen {ϕU1 U2} und {ϕ-1ϕU}
5. Der Spezialfall {P0, R0}
§2 Determiniertes Chiffratormodell
1. Definition von Abbildungen
2. Kryptologische Interpretation und elementare
Eigenschaften der Abbildungen
3. Periodizitätseigenschaften
3.1 Periodizität von Folgen
3.2 Die Periode der Folge r
3.3 Die Periode der Folge (Ui)i=0,1,2,…
3.4 Die Periode der Folge ( )a i=0,1,2,…
4. Analytische Abhängigkeiten
§3 Äquivalente Schlüssel
1. Grundlegende Definition
2. Äquivalente Schlüssel bezüglich der
Folge (Ui)i=1,2,…
3. Äquivalente Schlüssel bezüglich UN
4. Äquivalente Schlüssel bezüglich der
Folge (
)a i=0,1,2,…
4. Analytische Abhängigkeiten
§3 Äquivalente Schlüssel
1. Grundlegende Definition
2. Äquivalente Schlüssel bezüglich der
Folge (Ui)i=1,2,…
3. Äquivalente Schlüssel bezüglich UN
4. Äquivalente Schlüssel bezüglich der
Folge ( )i=1,2,…
§4 Stochastische Modelle der Chiffrierabbildung
1. Markowsche Kette
2. Ein anderes Modell
3. Experimentelle Untersuchung der statis-
tischen Eigenschaften der Additionsreihe
Kapitel V Einschätzung der Sicherheit des Chiffrators
Einleitung
§1 Methoden der Bestimmung des Schlüssels
§2 Kryptologische Auswirkungen technischer Fehler
1. Allgemeine Aussagen über technische Fehler
2. Technische Fehler im Chiffrator und bei der
Verarbeitung der Folge W
3. Kryptologisch schlechte Folge FU im Chif-
frator
3.1 Technische Fehler bei der Erzeugung von FU
3.2 Wahrscheinlichkeit gleicher F-Folgen-Ab-
schnitte im Ergebnis von Stromunterbrechung
4. Ausfall des Taktes t104 im Chiffrator und
im Prüf-Chiffrator
5. Verarbeitung fehlerhafter Schlüssel S
6. Technische Fehler in den Prüfbaugruppen,
-bausteinen und Baugruppen B1, B2
§3 Bedienungsfehler und deren Einfluß auf die
kryptologische Sicherheit
1. Mehrmalige Verwendung des gleichen Kurz-
zeitschlüssels S
2. Verwendung fehlerhafter Kurzzeitschlüssel S
3. Sonstige Bedienungsfehler
Zusammenfassung
1. Zusammenfassung der Resultate des Kapitels IV
2. Zusammenfassung der Resultate des Kapitels V
3. Das Schlüsselsystem und kryptologische Reserven
4. Richtungen der weiteren Untersuchungen der
kryptologischen Schaltung
Schlußfolgerungen
Literatur
Einleitung
Das System OPERATION wird entwickelt zur weiteren Automatisierung
des Gesamtkomplexes der Peilung von Funkstellen. Das System
OPERATION soll das System KRISTALL_QUARZ, welches auf der stra-
tegischen Ebene (Fernpeilung) eingesetzt wird, auf der taktischen
Ebene (Nah- und Nächstpeilung) ergänzen.
Das System OPERATION besteht aus einer Zentrale mit:
- einer Apparatur des Fahndungsstabes (2 Fahrzeuge)
- der Apparatur einer halbstationären Funkbeobachtungsstelle
mit max. 20 Horchposten (10 Fahrzeuge)
und mehreren (maximal 20) halbstationären und beweglichen
Peilpunkten (je ein Fahrzeug pro Peilpunkt).
Im einzelnen dient das System folgenden Zwecken:
a) in der Zentrale:
- der Eingabe und Aufbereitung von Kommandos zur Peilung
von Funkstationen;
- der automatischen Auswahl, Übernahme und Aufbereitung von
Kommandos, die über das System KRISTALL-QUARZ empfangen
werden;
- der Übertragung der aufbereiteten Kommandos;
b) in den Peilpunkten:
- dem Empfang und der Anzeige der Kommandos.
Der Prozeß der Übertragung und des Empfangs der Kommandos
verläuft nach folgendem Prinzip:
1. Stellt der Horchfunker eine Funkstation fest, tastet er ihr
wichtigstes Merkmal als Zusatzmitteilung ein (ein Merkmal
aus 100 möglichen).
2. Danach löst er über eine Taste die automatische Messung der
Frequenz der festgestellten Funkstation aus.
3. Die gemessene Frequenz wird automatisch an eine Zentralein-
heit übergeben, wo mittels Korrekturfrequenz automatisch die
vollständige Empfangsfrequenz bestimmt wird. Die vollständige
Empfangsfrequenz und die Zusatzmitteilung werden in der Zen-
traleinheit zwischengespeichert.
4. Von der Zentraleinheit wird dieses Kommando an die Einrich-
tungen zur Kodierung und Chiffrierung übergeben, wo die wei-
tere automatische Aufbereitung für die Übertragung erfolgt.
5. Die Kommandos werden 5 s. lang fortwährend wiederholt über-
tragen, sofern keine Unterbrechung erfolgt durch die notwen-
dig werdende Übertragung eines neuen Kommandos.
6. Die Kommandos gelangen über Leitungen, Kurzwellen- oder
Ultrakurzwellenkanäle zu den Empfangseinrichtungen der
Peilstationen. Hier werden sie automatisch dekodiert, de-
chiffriert und angezeigt.
Das System OPERATION ist für 24-Stunden-Betrieb ausgelegt.
Die zu übermittelnden Kommandos haben einen sehr hohen Geheim-
haltungsgrad, der durch das System OPERATION gehörende Chif-
friersystem gewährleistet werden muß.
Das System OPERATION wird in der DDR im Militärbereich des
Instituts für Regelungstechnik Berlin (IfR) entwickelt. Die
Mitarbeiter des IfR haben gewisse Erfahrungen auf dem Gebiet
der Entwicklung von automatisierten Kommandosystemen.
An der Entwicklung des Systems OPERATION arbeitet im IfR etwa
25 Entwicklungsingenieure. Die TTF für das System OPERATION
[1] wurden im Januar 1971 an das IfR übergeben. Der eigentliche
Beginn der Arbeiten im IfR war Herbst 1971. Im Dezember 1972
stand das AF2-Muster des Systems (die wesentlichsten Appara-
turen für eine Zentrale und zwei Peilpunkte) für die Labor-
erprobung bereit. Zum Ende des Jahres 1973 wird das K5-Muster
(die Apparaturen für eine Zentrale und 4 Peilstationen) fertig-
gestellt. Ab März 1974 ist die operative Erprobung des K5-
Musters vorgesehen. Während der Erprobung werden keine opera-
tiven Kommandos verarbeitet.
Das System OPERATION wurde auf der Grundlage der elektronischen
Bausteintechnik SN 54/74 der Firma Texas Instruments entwickelt.
Das AF2-Muster wurde mit diesen Baustein bestückt. Im K5-Muster
werden schon in größeren Umfang Modulbausteine der DDR-Baustein-
serie KME-10 verarbeitet. Diese Technik wird dann auch zum Bau
der Seriengeräte verwendet. Im Militärbereich des IfR arbeitet
eine Gruppe von Mitarbeitern, die vom ZCO der DDR entsprechend
den Bedingungen für das Chiffrierwesen bestätigt sind, an der
Entwicklung des Chiffriersystems für das System OPERATION.
Zu dieser Gruppe gehören 4 Diplomingenieure, 1 Mechaniker und
eine technische Zeichnerin. Zwischen dem ZCO der DDR und dieser
speziellen Gruppe im IfR besteht eine sehr enge Zusammenarbeit.
Die Arbeiten zur Entwicklung des Chiffriersystems im System
OPERATION wurden faktisch erst im November 1971 begonnen. An
der kryptologischen Entwicklung des Chiffriersystems konnten
im wesentlichen nur zwei Mitarbeiter des ZCO der DDR arbeiten.
Die Konzeption für das Chiffriersystem wurde vom ZCO am
20.12.1971 vorgelegt. Die allgemeine Konzeption der kryptolo-
gischen Schaltung für den Chiffrator (s. z. B. [3], Abb. 5)
wurde am 20.01.1972 festgelegt. Die kryptologische Schaltung
für den Chiffrator des AF2-Musters (s. z. B. [3], Abb. 1)
wurde am 25.05.1972 in allen Einzelheiten bestimmt. An der
Analyse des Chiffrators für das AF2-Muster konnten nur
zwei Genossen des ZCO der DDR arbeiten.
Auf der Beratung zwischen Genossen des ZCO der UdSSR und des
ZCO der DDR, die im Rahmen der Beratung zur Vorstellung des
AF2-Musters von der Gruppe der Koordinierung vom 27.02. -
03.03.1973 in Berlin stattfand, wurde eingeschätzt (s. [4]),
daß der Chiffrator des AF2-Musters die geforderte Sicherheit
nicht gewährleistet.
Die aus Sicht des ZCO der DDR notwendig erscheinenden Änderungen
der kryptologischen Schaltung (s.[5]) wurde am 02.04.1973
festgelegt. An der hier vorliegenden Analyse dieser neuen
kryptologischen Schaltung arbeitete im ZCO der DDR eine Gruppe
mit 5 Diplommathematikern und einem Programmierer. An der Pro-
grammierung der statistischen Kontrolle der Additionsreihe
arbeitete zeitweise noch ein zweiter Programmierer. Er ge-
hörte nicht zur Gruppe. Der Leiter der Gruppe hat die Quali-
fikation, Kandidat der Wissenschaften. Zwei der 5 Mathematiker
haben erst im Jahre 1972 ihr Studium beendet. Der Programmierer
der Gruppe hat in der Programmierung des zur Verfügung stehenden
Rechners vom Typ
)i=1,2,…
§4 Stochastische Modelle der Chiffrierabbildung
1. Markowsche Kette
2. Ein anderes Modell
3. Experimentelle Untersuchung der statis-
tischen Eigenschaften der Additionsreihe
Kapitel V Einschätzung der Sicherheit des Chiffrators
Einleitung
§1 Methoden der Bestimmung des Schlüssels
§2 Kryptologische Auswirkungen technischer Fehler
1. Allgemeine Aussagen über technische Fehler
2. Technische Fehler im Chiffrator und bei der
Verarbeitung der Folge W
3. Kryptologisch schlechte Folge FU im Chif-
frator
3.1 Technische Fehler bei der Erzeugung von FU
3.2 Wahrscheinlichkeit gleicher F-Folgen-Ab-
schnitte im Ergebnis von Stromunterbrechung
4. Ausfall des Taktes t104 im Chiffrator und
im Prüf-Chiffrator
5. Verarbeitung fehlerhafter Schlüssel S
6. Technische Fehler in den Prüfbaugruppen,
-bausteinen und Baugruppen B1, B2
§3 Bedienungsfehler und deren Einfluß auf die
kryptologische Sicherheit
1. Mehrmalige Verwendung des gleichen Kurz-
zeitschlüssels S
2. Verwendung fehlerhafter Kurzzeitschlüssel S
3. Sonstige Bedienungsfehler
Zusammenfassung
1. Zusammenfassung der Resultate des Kapitels IV
2. Zusammenfassung der Resultate des Kapitels V
3. Das Schlüsselsystem und kryptologische Reserven
4. Richtungen der weiteren Untersuchungen der
kryptologischen Schaltung
Schlußfolgerungen
Literatur
Einleitung
Das System OPERATION wird entwickelt zur weiteren Automatisierung
des Gesamtkomplexes der Peilung von Funkstellen. Das System
OPERATION soll das System KRISTALL_QUARZ, welches auf der stra-
tegischen Ebene (Fernpeilung) eingesetzt wird, auf der taktischen
Ebene (Nah- und Nächstpeilung) ergänzen.
Das System OPERATION besteht aus einer Zentrale mit:
- einer Apparatur des Fahndungsstabes (2 Fahrzeuge)
- der Apparatur einer halbstationären Funkbeobachtungsstelle
mit max. 20 Horchposten (10 Fahrzeuge)
und mehreren (maximal 20) halbstationären und beweglichen
Peilpunkten (je ein Fahrzeug pro Peilpunkt).
Im einzelnen dient das System folgenden Zwecken:
a) in der Zentrale:
- der Eingabe und Aufbereitung von Kommandos zur Peilung
von Funkstationen;
- der automatischen Auswahl, Übernahme und Aufbereitung von
Kommandos, die über das System KRISTALL-QUARZ empfangen
werden;
- der Übertragung der aufbereiteten Kommandos;
b) in den Peilpunkten:
- dem Empfang und der Anzeige der Kommandos.
Der Prozeß der Übertragung und des Empfangs der Kommandos
verläuft nach folgendem Prinzip:
1. Stellt der Horchfunker eine Funkstation fest, tastet er ihr
wichtigstes Merkmal als Zusatzmitteilung ein (ein Merkmal
aus 100 möglichen).
2. Danach löst er über eine Taste die automatische Messung der
Frequenz der festgestellten Funkstation aus.
3. Die gemessene Frequenz wird automatisch an eine Zentralein-
heit übergeben, wo mittels Korrekturfrequenz automatisch die
vollständige Empfangsfrequenz bestimmt wird. Die vollständige
Empfangsfrequenz und die Zusatzmitteilung werden in der Zen-
traleinheit zwischengespeichert.
4. Von der Zentraleinheit wird dieses Kommando an die Einrich-
tungen zur Kodierung und Chiffrierung übergeben, wo die wei-
tere automatische Aufbereitung für die Übertragung erfolgt.
5. Die Kommandos werden 5 s. lang fortwährend wiederholt über-
tragen, sofern keine Unterbrechung erfolgt durch die notwen-
dig werdende Übertragung eines neuen Kommandos.
6. Die Kommandos gelangen über Leitungen, Kurzwellen- oder
Ultrakurzwellenkanäle zu den Empfangseinrichtungen der
Peilstationen. Hier werden sie automatisch dekodiert, de-
chiffriert und angezeigt.
Das System OPERATION ist für 24-Stunden-Betrieb ausgelegt.
Die zu übermittelnden Kommandos haben einen sehr hohen Geheim-
haltungsgrad, der durch das System OPERATION gehörende Chif-
friersystem gewährleistet werden muß.
Das System OPERATION wird in der DDR im Militärbereich des
Instituts für Regelungstechnik Berlin (IfR) entwickelt. Die
Mitarbeiter des IfR haben gewisse Erfahrungen auf dem Gebiet
der Entwicklung von automatisierten Kommandosystemen.
An der Entwicklung des Systems OPERATION arbeitet im IfR etwa
25 Entwicklungsingenieure. Die TTF für das System OPERATION
[1] wurden im Januar 1971 an das IfR übergeben. Der eigentliche
Beginn der Arbeiten im IfR war Herbst 1971. Im Dezember 1972
stand das AF2-Muster des Systems (die wesentlichsten Appara-
turen für eine Zentrale und zwei Peilpunkte) für die Labor-
erprobung bereit. Zum Ende des Jahres 1973 wird das K5-Muster
(die Apparaturen für eine Zentrale und 4 Peilstationen) fertig-
gestellt. Ab März 1974 ist die operative Erprobung des K5-
Musters vorgesehen. Während der Erprobung werden keine opera-
tiven Kommandos verarbeitet.
Das System OPERATION wurde auf der Grundlage der elektronischen
Bausteintechnik SN 54/74 der Firma Texas Instruments entwickelt.
Das AF2-Muster wurde mit diesen Baustein bestückt. Im K5-Muster
werden schon in größeren Umfang Modulbausteine der DDR-Baustein-
serie KME-10 verarbeitet. Diese Technik wird dann auch zum Bau
der Seriengeräte verwendet. Im Militärbereich des IfR arbeitet
eine Gruppe von Mitarbeitern, die vom ZCO der DDR entsprechend
den Bedingungen für das Chiffrierwesen bestätigt sind, an der
Entwicklung des Chiffriersystems für das System OPERATION.
Zu dieser Gruppe gehören 4 Diplomingenieure, 1 Mechaniker und
eine technische Zeichnerin. Zwischen dem ZCO der DDR und dieser
speziellen Gruppe im IfR besteht eine sehr enge Zusammenarbeit.
Die Arbeiten zur Entwicklung des Chiffriersystems im System
OPERATION wurden faktisch erst im November 1971 begonnen. An
der kryptologischen Entwicklung des Chiffriersystems konnten
im wesentlichen nur zwei Mitarbeiter des ZCO der DDR arbeiten.
Die Konzeption für das Chiffriersystem wurde vom ZCO am
20.12.1971 vorgelegt. Die allgemeine Konzeption der kryptolo-
gischen Schaltung für den Chiffrator (s. z. B. [3], Abb. 5)
wurde am 20.01.1972 festgelegt. Die kryptologische Schaltung
für den Chiffrator des AF2-Musters (s. z. B. [3], Abb. 1)
wurde am 25.05.1972 in allen Einzelheiten bestimmt. An der
Analyse des Chiffrators für das AF2-Muster konnten nur
zwei Genossen des ZCO der DDR arbeiten.
Auf der Beratung zwischen Genossen des ZCO der UdSSR und des
ZCO der DDR, die im Rahmen der Beratung zur Vorstellung des
AF2-Musters von der Gruppe der Koordinierung vom 27.02. -
03.03.1973 in Berlin stattfand, wurde eingeschätzt (s. [4]),
daß der Chiffrator des AF2-Musters die geforderte Sicherheit
nicht gewährleistet.
Die aus Sicht des ZCO der DDR notwendig erscheinenden Änderungen
der kryptologischen Schaltung (s.[5]) wurde am 02.04.1973
festgelegt. An der hier vorliegenden Analyse dieser neuen
kryptologischen Schaltung arbeitete im ZCO der DDR eine Gruppe
mit 5 Diplommathematikern und einem Programmierer. An der Pro-
grammierung der statistischen Kontrolle der Additionsreihe
arbeitete zeitweise noch ein zweiter Programmierer. Er ge-
hörte nicht zur Gruppe. Der Leiter der Gruppe hat die Quali-
fikation, Kandidat der Wissenschaften. Zwei der 5 Mathematiker
haben erst im Jahre 1972 ihr Studium beendet. Der Programmierer
der Gruppe hat in der Programmierung des zur Verfügung stehenden
Rechners vom Typ 
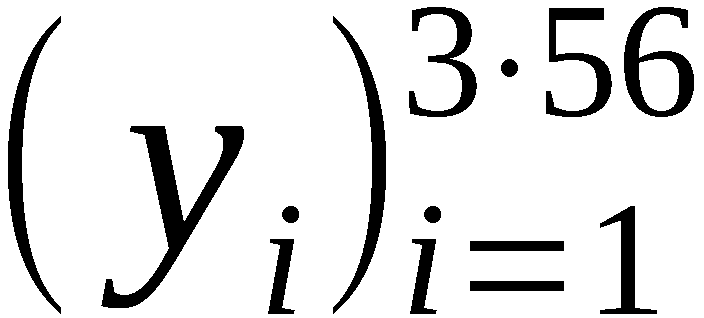 (y
(y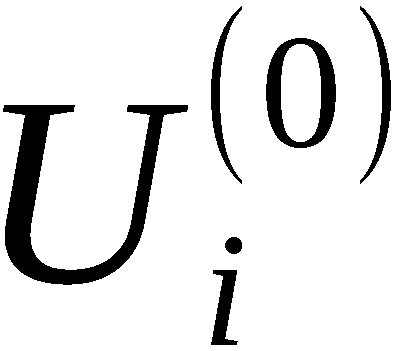 = U
= U über.
Unter Einwirkung des Elements FU
über.
Unter Einwirkung des Elements FU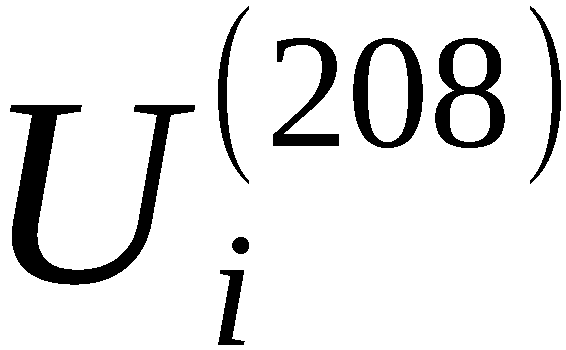 über. Und so
weiter bis zum Übertragungstakt T
über. Und so
weiter bis zum Übertragungstakt T
 ) ∈ {0,1}
) ∈ {0,1}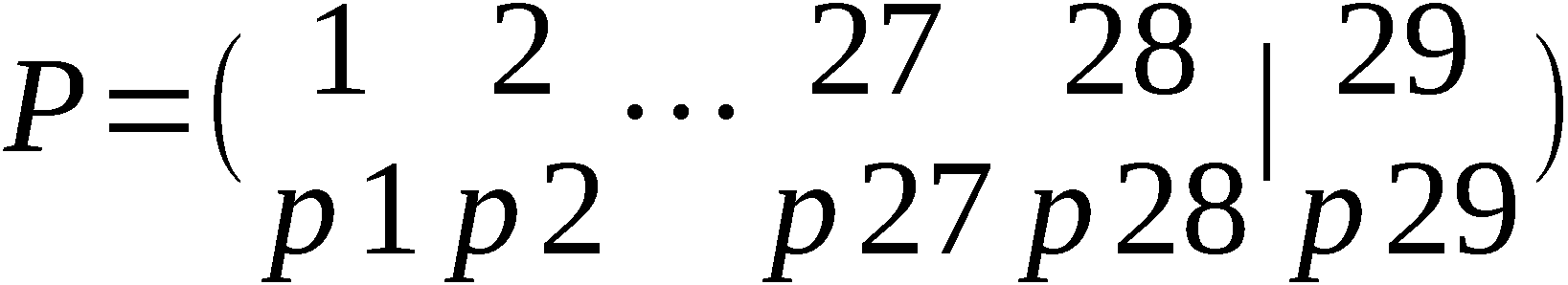 - Kommutator
umkehrbar eindeutige Verknüpfung der Ausgänge V
- Kommutator
umkehrbar eindeutige Verknüpfung der Ausgänge V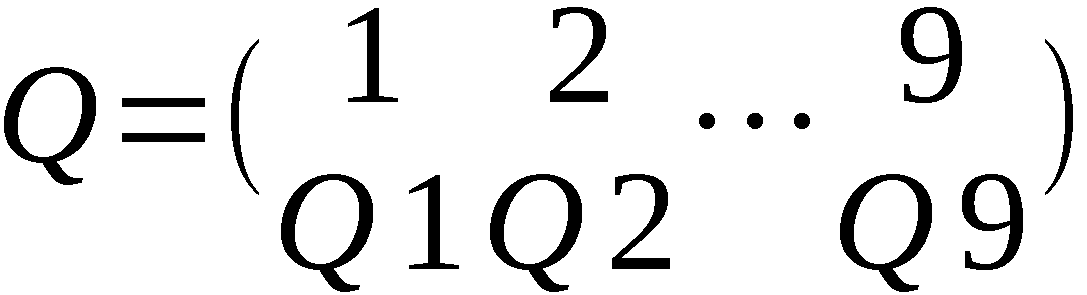 - Kommutator (Permutation 10 x 10)
umkehrbar eindeutige Verknüpfung der Ausgänge tɳ mit
den Eingängen r
- Kommutator (Permutation 10 x 10)
umkehrbar eindeutige Verknüpfung der Ausgänge tɳ mit
den Eingängen r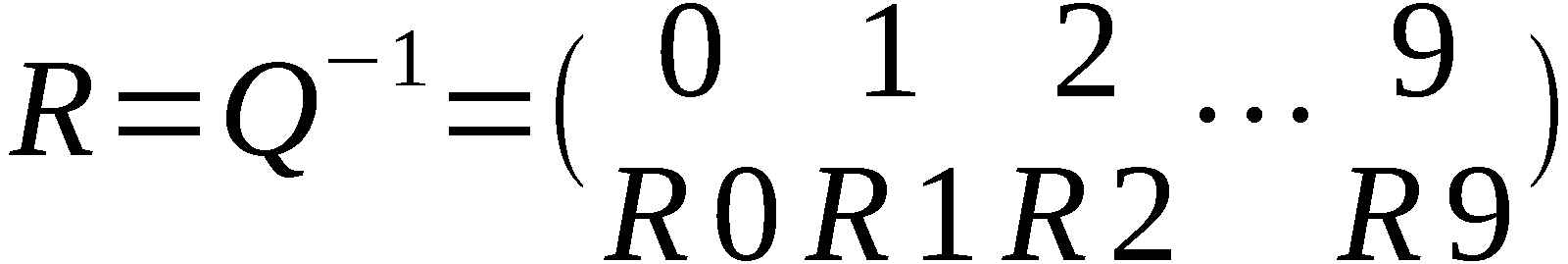 .
.

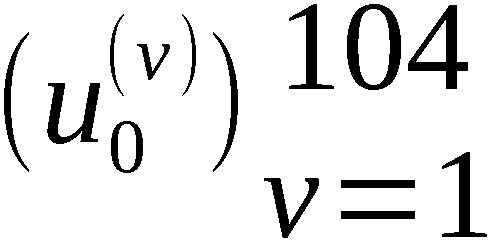 und S
und S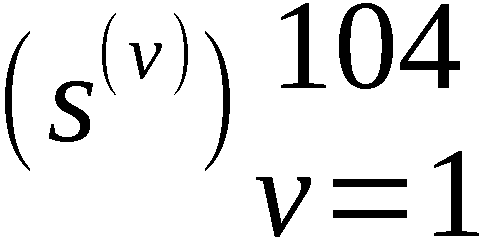 enthalten.
Im Zeitintervall [t
enthalten.
Im Zeitintervall [t des Speicherelements U
des Speicherelements U , s
, s
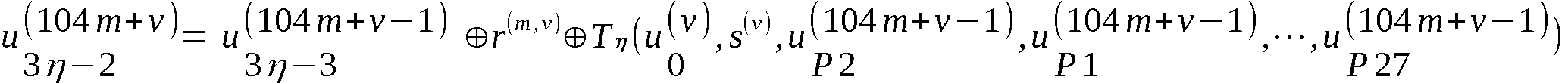 (ɳ=2,3,…,9),
(ɳ=2,3,…,9),
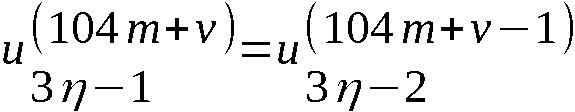 (ɳ=1,2,…,9),
(ɳ=1,2,…,9),
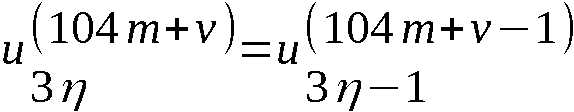 ,
,
 .
Dabei sind die Tɳ = Tɳ(e
.
Dabei sind die Tɳ = Tɳ(e
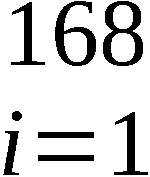 geschlossen. Die im Zufallsgenerator ZG erzeugte
Folge (y
geschlossen. Die im Zufallsgenerator ZG erzeugte
Folge (y
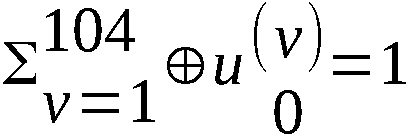 ,
, erfüllt ist. (s. auch Kap. III, §2.).
Im Prüfbaustein P-E-S1/S2 wird nur bei der Eingabe des
Schlüssels S in SRS1/SRS2 überprüft, ob die Bedingungen
erfüllt ist. (s. auch Kap. III, §2.).
Im Prüfbaustein P-E-S1/S2 wird nur bei der Eingabe des
Schlüssels S in SRS1/SRS2 überprüft, ob die Bedingungen
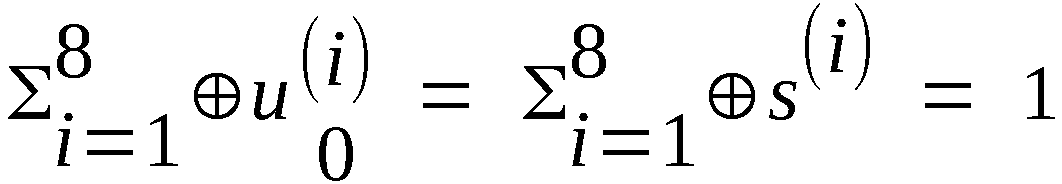
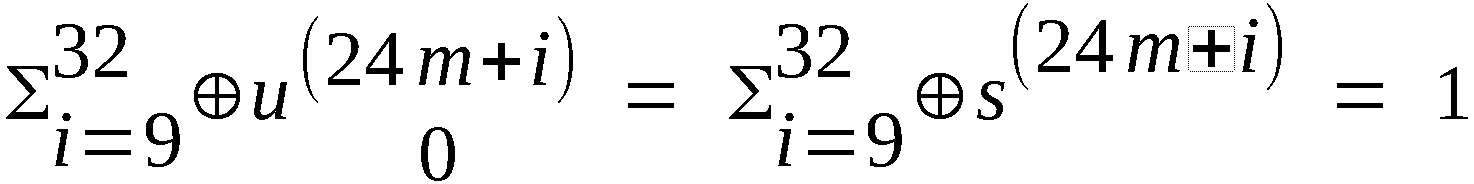 (m = 0, 1, 2, 3)
erfüllt sind.
Im Baustein P-SE werden entsprechend der Eingabesituation
des Schlüssels S (Eingabe richtig abgeschlossen oder nicht)
die Signale FGSE und M4-SE gebildet (s. Kap. II, §3, 1.).
Ein in P-t104 oder P-S1/S2 erkannter Fehler führt immer
entweder zu FGSE = 0 oder M4-SE = L.
Ein in P-E-S1/S2 erkannter Fehler führt immer dazu, daß
FGSE=0 nicht aufgehoben wird.
Im Prüfbaustein P-FGFU wird überprüft, ob pro Übertragungs-
takt ein endliches Freigabesignal übernommen wird.
Vom Chiffrator und vom Prüf-Chiffrator werden in jedem
Übertragungstakt FÜ
(m = 0, 1, 2, 3)
erfüllt sind.
Im Baustein P-SE werden entsprechend der Eingabesituation
des Schlüssels S (Eingabe richtig abgeschlossen oder nicht)
die Signale FGSE und M4-SE gebildet (s. Kap. II, §3, 1.).
Ein in P-t104 oder P-S1/S2 erkannter Fehler führt immer
entweder zu FGSE = 0 oder M4-SE = L.
Ein in P-E-S1/S2 erkannter Fehler führt immer dazu, daß
FGSE=0 nicht aufgehoben wird.
Im Prüfbaustein P-FGFU wird überprüft, ob pro Übertragungs-
takt ein endliches Freigabesignal übernommen wird.
Vom Chiffrator und vom Prüf-Chiffrator werden in jedem
Übertragungstakt FÜ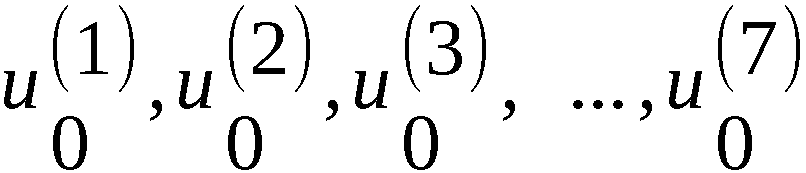
 (m = 0, 1, 2, 3),
S
(m = 0, 1, 2, 3),
S ⊕ u
⊕ u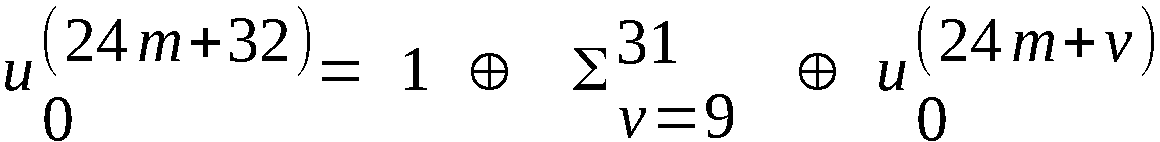 (m = 0, 1, 2, 3)
(m = 0, 1, 2, 3)
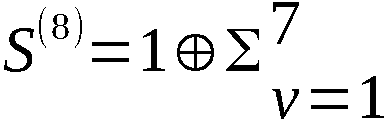 ⊕ S
⊕ S ⊕ S
⊕ S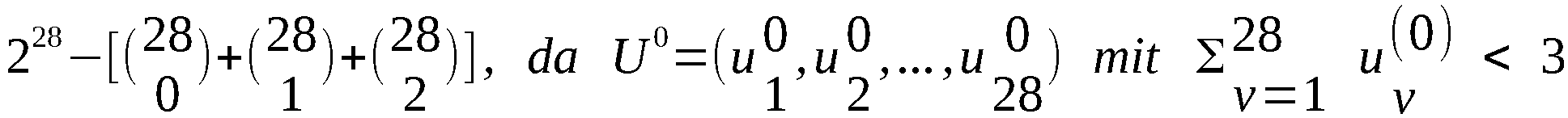 technisch nicht realisierbar ist.
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der kryptologischen Schaltung
Ausgehend von den Forderungen zur Entwicklung eines Chif-
friersystems für das System OPERATION wurde eine krypto-
logische Schaltung I für den Chiffrator entwickelt. Diese
kryptologische Schaltung ist in [3] beschrieben und be-
gründet.
Nach einer ersten vorläufigen Analyse dieser kryptolo-
gischen Schaltung I durch das ZCO der UdSSR (siehe [4])
wurde festgestellt, daß die kryptologische Sicherheit
der Nachrichten bei dieser Schaltung nicht gewährleistet
ist.
Als wesentliche Schwächen wurden erkannt (siehe [4]):
(1) die geringe effektive Schlüsselvorrat;
(2) die ungleichmäßige Mächtigkeit der Klassen äquiva-
lenter Schlüssel;
(3) die Existenz einer großen Anzahl von Schlüsseln, die
inbezug auf die statistischen Eigenschaften der den
Prozeß der Zustandsänderung des Chiffrators beschrei-
benden Markoffschen Kette und damit vermutlich auch
in Bezug auf die statistische Eigenschaften der Ad-
ditionsreihen, schlecht sind.
Die Überwindung dieser schwächen unter Beibehaltung der
wesentlichen Festlegungen der Konzeption des Chiffrier-
systems und des Volumens insbesondere für die Dechif-
friereinrichtung, war der Ausgangspunkt für die Ent-
wicklung der kryptologischen Schaltung des Chiffrators
in der jetzt vorliegenden Gestalt (Schaltung II).
2. Festlegung des Schlüsselsystems
Die gegenwärtig verfügbaren Kommutatoren sind aufgrund
ihrer mechanischen, elektrischen und klimatischen Eigen-
schaften oder aufgrund ihres großen Volumens als Schlüs-
seleingabevorrichtungen für den Einsatz in den Chiffrier-
und Dechiffriereinrichtungen des Systems OPERATION nicht
geeignet.
Es besteht gegenwärtig auch keine Aussicht, einsatzfähige
Kommutatoren in entsprechend kurzer Zeit zu entwickeln.
Kommutatoren sind deshalb im Prinzip zur Zeit nur zur
Realisierung von Langzeitschlüsseln geeignet.
Im Gegensatz dazu war es möglich, in relativ kurzer Zeit
eine optoelektronische Vorrichtung zur Einspeicherung von
0,1-Folgen zu entwickeln, die die Forderungen an eine
Schlüsseleingabevorrichtung im Chiffriersystem von
OPERATION erfüllt.
Ausgehend von diesen technischen Bedingungen wurde fest-
gelegt, 0,1-Folgen als Kurzzeitschlüssel zu benutzen.
Zur Erhöhung der kryptologischen Sicherheit des Chiffrators
erscheint es günstig, diesen Kurzzeitschlüssel mit einem
Langzeitschlüssel, speziell mit einem durch Kommutatoren
realisierten Langzeitschlüssel, zu kombinieren.
3. Grundprinzip der Erzeugung der Folge W
In der vorläufigen Analyse der kryptologischen Schaltung I
wurde festgelegt, daß die in dieser Schaltung realisierte
Umformung der Eingangsfolge FU
technisch nicht realisierbar ist.
§3 Begründung der kryptologischen Schaltung
1. Ausgangspunkt für die Entwicklung der kryptologischen Schaltung
Ausgehend von den Forderungen zur Entwicklung eines Chif-
friersystems für das System OPERATION wurde eine krypto-
logische Schaltung I für den Chiffrator entwickelt. Diese
kryptologische Schaltung ist in [3] beschrieben und be-
gründet.
Nach einer ersten vorläufigen Analyse dieser kryptolo-
gischen Schaltung I durch das ZCO der UdSSR (siehe [4])
wurde festgestellt, daß die kryptologische Sicherheit
der Nachrichten bei dieser Schaltung nicht gewährleistet
ist.
Als wesentliche Schwächen wurden erkannt (siehe [4]):
(1) die geringe effektive Schlüsselvorrat;
(2) die ungleichmäßige Mächtigkeit der Klassen äquiva-
lenter Schlüssel;
(3) die Existenz einer großen Anzahl von Schlüsseln, die
inbezug auf die statistischen Eigenschaften der den
Prozeß der Zustandsänderung des Chiffrators beschrei-
benden Markoffschen Kette und damit vermutlich auch
in Bezug auf die statistische Eigenschaften der Ad-
ditionsreihen, schlecht sind.
Die Überwindung dieser schwächen unter Beibehaltung der
wesentlichen Festlegungen der Konzeption des Chiffrier-
systems und des Volumens insbesondere für die Dechif-
friereinrichtung, war der Ausgangspunkt für die Ent-
wicklung der kryptologischen Schaltung des Chiffrators
in der jetzt vorliegenden Gestalt (Schaltung II).
2. Festlegung des Schlüsselsystems
Die gegenwärtig verfügbaren Kommutatoren sind aufgrund
ihrer mechanischen, elektrischen und klimatischen Eigen-
schaften oder aufgrund ihres großen Volumens als Schlüs-
seleingabevorrichtungen für den Einsatz in den Chiffrier-
und Dechiffriereinrichtungen des Systems OPERATION nicht
geeignet.
Es besteht gegenwärtig auch keine Aussicht, einsatzfähige
Kommutatoren in entsprechend kurzer Zeit zu entwickeln.
Kommutatoren sind deshalb im Prinzip zur Zeit nur zur
Realisierung von Langzeitschlüsseln geeignet.
Im Gegensatz dazu war es möglich, in relativ kurzer Zeit
eine optoelektronische Vorrichtung zur Einspeicherung von
0,1-Folgen zu entwickeln, die die Forderungen an eine
Schlüsseleingabevorrichtung im Chiffriersystem von
OPERATION erfüllt.
Ausgehend von diesen technischen Bedingungen wurde fest-
gelegt, 0,1-Folgen als Kurzzeitschlüssel zu benutzen.
Zur Erhöhung der kryptologischen Sicherheit des Chiffrators
erscheint es günstig, diesen Kurzzeitschlüssel mit einem
Langzeitschlüssel, speziell mit einem durch Kommutatoren
realisierten Langzeitschlüssel, zu kombinieren.
3. Grundprinzip der Erzeugung der Folge W
In der vorläufigen Analyse der kryptologischen Schaltung I
wurde festgelegt, daß die in dieser Schaltung realisierte
Umformung der Eingangsfolge FU
 -Zustandsmenge) des Chiffrators, E-Eingabemenge des
Chiffrators) des Chiffrators.
Bei der weiteren Präzisierung der Struktur des Chiffrators
mußte folgende Beschränkungen des Volumens des Chiffrators
beachtet werden:
Zur Realisierung des Chiffrators (U
-Zustandsmenge) des Chiffrators, E-Eingabemenge des
Chiffrators) des Chiffrators.
Bei der weiteren Präzisierung der Struktur des Chiffrators
mußte folgende Beschränkungen des Volumens des Chiffrators
beachtet werden:
Zur Realisierung des Chiffrators (U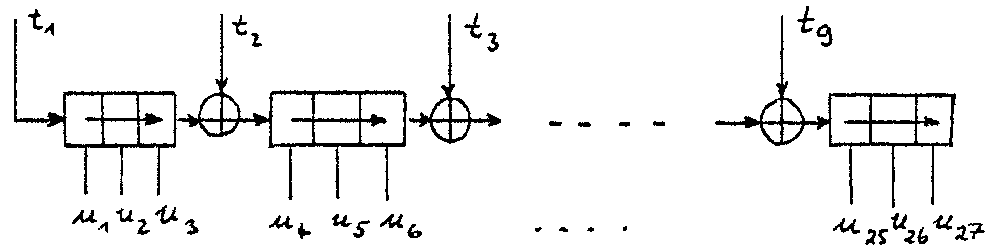

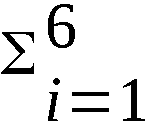 x
x )*1/2 (r = 0,1, …, 6)
(3) |{x = (x
)*1/2 (r = 0,1, …, 6)
(3) |{x = (x
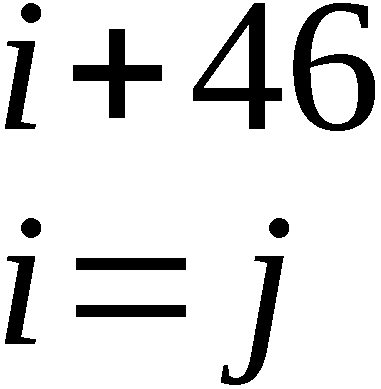 von W werden
alle Zusammenhänge zwischen (FU
von W werden
alle Zusammenhänge zwischen (FU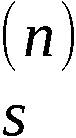 (n = 0, 1,…, 46) mit
B
(n = 0, 1,…, 46) mit
B = (u
= (u ,
, 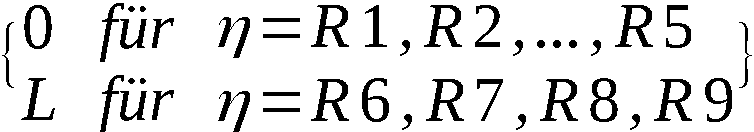 Die Abbildung ϕ = ϕ(u
Die Abbildung ϕ = ϕ(u * 2! = 8! * 5400.
Es sind 18 Elemente von P beliebig.
Deshalb gilt
(D
* 2! = 8! * 5400.
Es sind 18 Elemente von P beliebig.
Deshalb gilt
(D *
* 
 = y
= y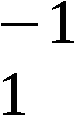 U = U
U = U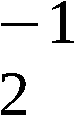 = U, U
= U, U ϕ
ϕ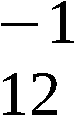 … ϕ
… ϕ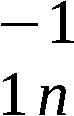 U
U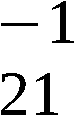 ϕ
ϕ … ϕ
… ϕ U
U ,
V = ϕ(u
,
V = ϕ(u = u
= u = u
= u +r
+r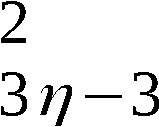 +r
+r = u
= u ,r'
,r' ,s
,s ,s
,s ,s
,s ,r
,r ,s
,s ,r
,r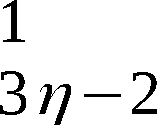 +y
+y + X
+ X + y
+ y + y
+ y + y
+ y + y
+ y + y
+ y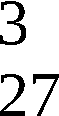 + y
+ y + y
+ y + y
+ y + y
+ y = U
= U = … = U
= … = U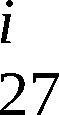 = 0
genügen.
Bis zum 10. Oktober 1973 wurde nach 35 Stunden Rechenzeit
i ≈ 27,7 * 10
= 0
genügen.
Bis zum 10. Oktober 1973 wurde nach 35 Stunden Rechenzeit
i ≈ 27,7 * 10 = {0,1}
= {0,1} = {0,1}
= {0,1} ),(s
),(s ,s
,s ), …,(s
), …,(s ,s
,s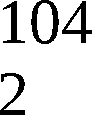 )).
Wenn für S ∈
)).
Wenn für S ∈  dann sind diese S Elemente der Teilmenge
dann sind diese S Elemente der Teilmenge  der Menge
der Menge  )
) werden rekurrent nach der Formel
s
werden rekurrent nach der Formel
s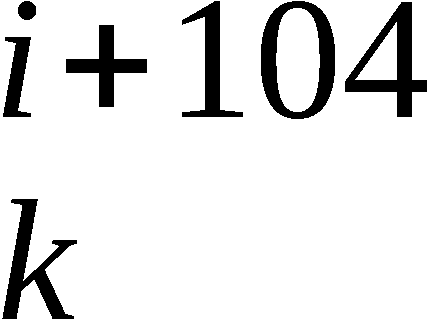 s
s wird rekurrent nach der
Formel f
wird rekurrent nach der
Formel f bezeichnen wir die Menge aller F ∈
bezeichnen wir die Menge aller F ∈ 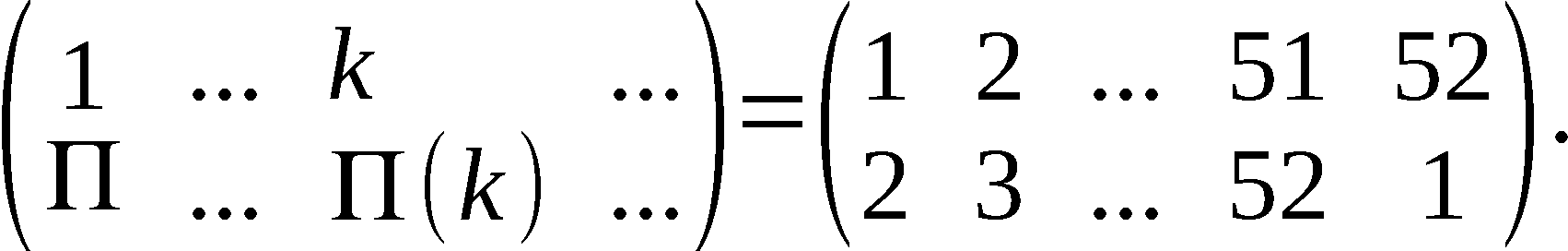 Schließlich führen wir noch folgende Bezeichnungen ein:
Schließlich führen wir noch folgende Bezeichnungen ein:
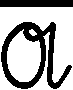 ={0,1}
={0,1} ,s
,s ,r
,r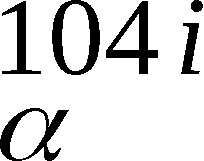 = a
= a = A
= A

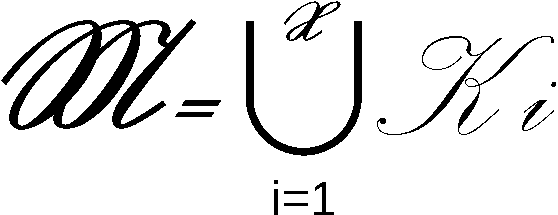 , i ≠ j :
, i ≠ j : Analog kann man die Zustandsklassen von Φ definieren,
wobei S ∈
Analog kann man die Zustandsklassen von Φ definieren,
wobei S ∈  , i ≠ j :
, i ≠ j :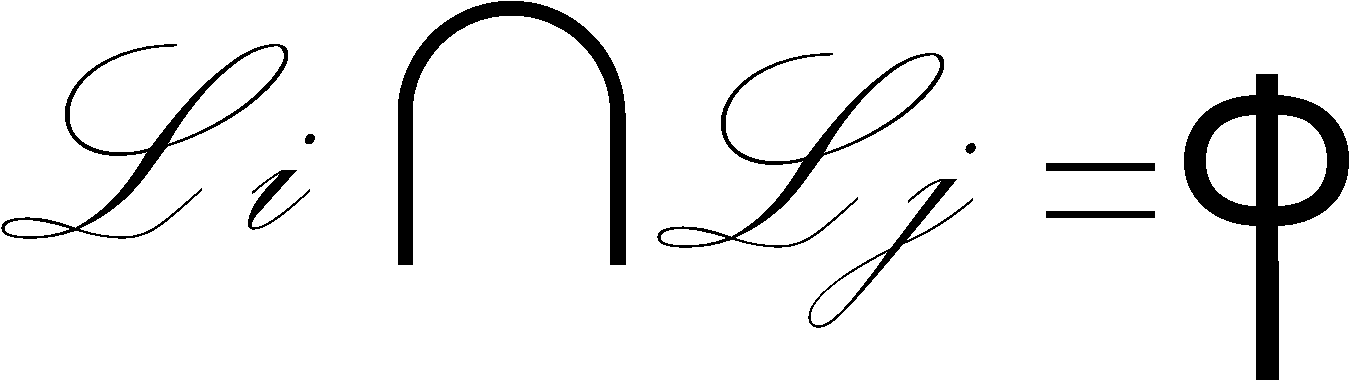 Dann ist leicht zu sehen, daß
Dann ist leicht zu sehen, daß  gilt, und jede Klasse
K
gilt, und jede Klasse
K
 ) ∈
) ∈  (F) = u
(F) = u + f
+ f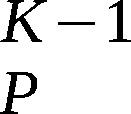 )
u
)
u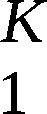 + s
+ s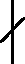 b bedeutet das Gegenteil.)
In der Tat,
sei d
b bedeutet das Gegenteil.)
In der Tat,
sei d  = u
= u + r
+ r = u
= u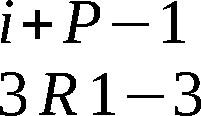 + r
+ r = u
= u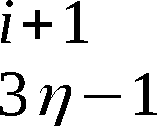 = u
= u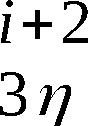 gilt
P
gilt
P (u
(u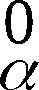 ,…,s
,…,s (u
(u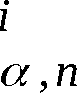 , α =
, α = 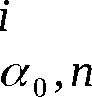 , α=
, α=  , α=
, α=  , α=
, α=  beziehungsweise (U
beziehungsweise (U , der Folge (U
, der Folge (U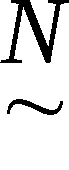 S' benutzen.
Bei N < 104 sind offensichtlich alle Schlüssel, die sich von-
einander nur in den Stellen N+1, N+2, … , 104 unterscheiden,
äquivalent bezüglich U
S' benutzen.
Bei N < 104 sind offensichtlich alle Schlüssel, die sich von-
einander nur in den Stellen N+1, N+2, … , 104 unterscheiden,
äquivalent bezüglich U S'.
Wünschenswert wäre es, eine notwendige und hinreichende
Bedingung für die Existenz äquivalenter Schlüssel bezüglich
U
S'.
Wünschenswert wäre es, eine notwendige und hinreichende
Bedingung für die Existenz äquivalenter Schlüssel bezüglich
U , V = (v
, V = (v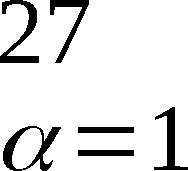 ∈
∈ 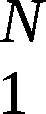 hat folgende Darstellung
u
hat folgende Darstellung
u ∆
∆ ) =
= s
) =
= s ,s
,s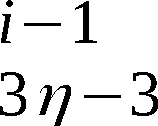 +r
+r ).
Daraus wird unmittelbar klar, daß u
).
Daraus wird unmittelbar klar, daß u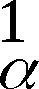 und u
und u ).
2.2 Dieses Modell unterscheidet sich von der kryptologischen
Schaltung weniger, als die in Punkt 1 untersuchte Markowsche
Kette, aber es wurde ein stärkeres Ergebnis erhalten. Der
Unterschied zur kryptologischen Schaltung besteht nur darin,
daß in ihr (r
).
2.2 Dieses Modell unterscheidet sich von der kryptologischen
Schaltung weniger, als die in Punkt 1 untersuchte Markowsche
Kette, aber es wurde ein stärkeres Ergebnis erhalten. Der
Unterschied zur kryptologischen Schaltung besteht nur darin,
daß in ihr (r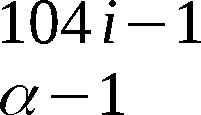 + r
+ r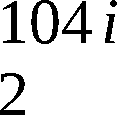 ∆
∆ )
r
)
r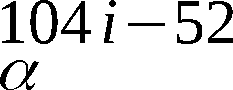 ein
und wirkt auf U
ein
und wirkt auf U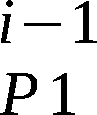 , …, u
, …, u )
von s
)
von s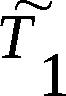 (u
(u ,s
,s )) ∈ {0,1}
)) ∈ {0,1} ,s
,s ). Entweder stimmt keine der beiden
mit (s
). Entweder stimmt keine der beiden
mit (s S eindeutig
bestimmen.
Wir bemerken, daß man in der Praxis diesen Weg nicht
realisieren kann, da man ≈10
S eindeutig
bestimmen.
Wir bemerken, daß man in der Praxis diesen Weg nicht
realisieren kann, da man ≈10 = Ψ
= Ψ 4. Ausfall des Taktes t104 im Chiffrator und im Prüf-Chiffrator
Bei Ausfall des Taktes t104 im Chiffrator ändert sich der
innere Zustand im Chiffrator nicht, d.h. der Inhalt des
Speicherelements U
4. Ausfall des Taktes t104 im Chiffrator und im Prüf-Chiffrator
Bei Ausfall des Taktes t104 im Chiffrator ändert sich der
innere Zustand im Chiffrator nicht, d.h. der Inhalt des
Speicherelements U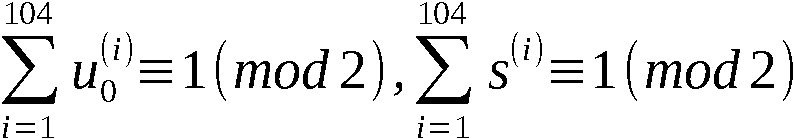 erfüllt ist. Diese Bedingung ist nicht erfüllt, wenn S
erfüllt ist. Diese Bedingung ist nicht erfüllt, wenn S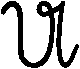 -Registers)
Es wird empfohlen, U
-Registers)
Es wird empfohlen, U ,u
,u , …, u
, …, u ) = (000 000 011 011 111 111 111 100 000 000)
empfohlen. Dieser Wert U
) = (000 000 011 011 111 111 111 100 000 000)
empfohlen. Dieser Wert U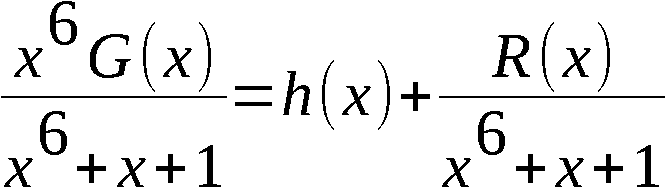 wo h(x) ein Polynom ist, liefert das Polynom
R(x) = g
wo h(x) ein Polynom ist, liefert das Polynom
R(x) = g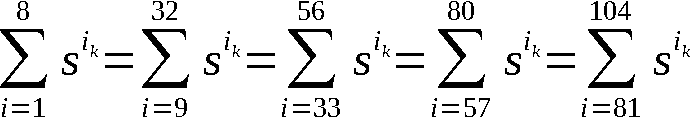 (k = 1,2).
siehe [1; III, §2,1.]
3.3. Die logischen Funktionen h
(k = 1,2).
siehe [1; III, §2,1.]
3.3. Die logischen Funktionen h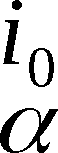 nicht riesig und überschaubar sind. Es
wird erwartet, daß i
nicht riesig und überschaubar sind. Es
wird erwartet, daß i , i =
, i =  = 1.
Dabei ist (P,R) = P
= 1.
Dabei ist (P,R) = P , j =
, j =  - Anzahl der Einsen in A
- Anzahl der Einsen in A .
t
.
t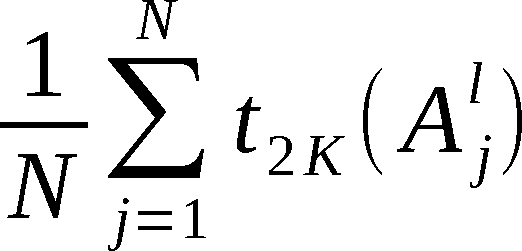 t
t , K =
, K = 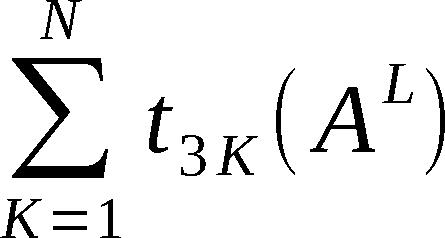 (Anzahl der Serein in A
(Anzahl der Serein in A
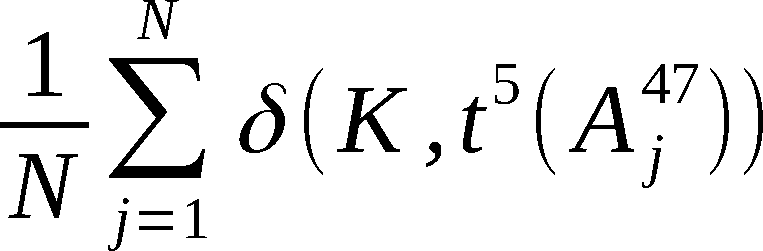 , K =
, K = 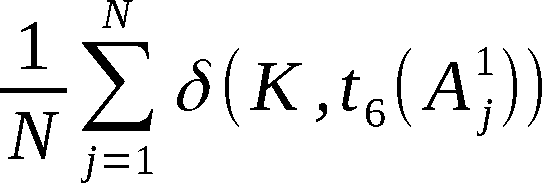 , K =
, K = 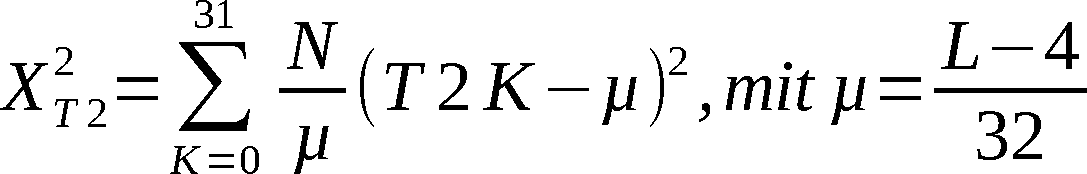 ;
;
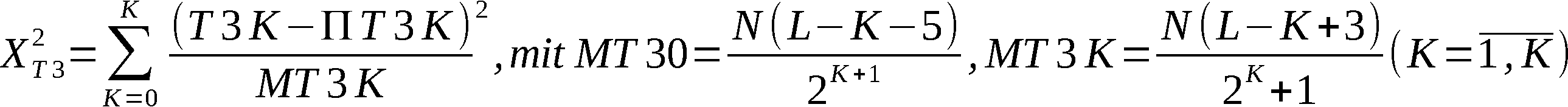 ;
T2(δ), δ = 1, 2, 3 - die Zahl der Werte T2K im Intervall
;
T2(δ), δ = 1, 2, 3 - die Zahl der Werte T2K im Intervall
 .
Variante C
Sie berechnet und gibt aus T1 für L = 1.
Variante D
Sie berechnet und gibt aus T5K, K =
.
Variante C
Sie berechnet und gibt aus T1 für L = 1.
Variante D
Sie berechnet und gibt aus T5K, K = 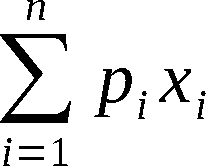 und Dξ = M(ξ - Mξ)
und Dξ = M(ξ - Mξ)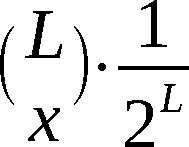 x =
x = 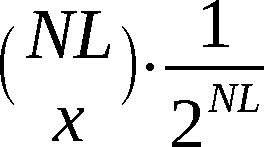 x =
x =  ], mit Wahrscheinlichkeit
≈ 96 % im Intervall [
], mit Wahrscheinlichkeit
≈ 96 % im Intervall [ ] und mit Wah-
scheinlichkeit ≈ 97 % im Intervall [
] und mit Wah-
scheinlichkeit ≈ 97 % im Intervall [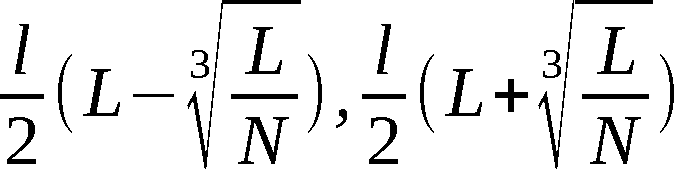 ]
liegen.
Die Statistik T2K überprüft die Häufigkeit des Auftretens
der Polygramme der Länge 5. Abweichungen von den theoretischen
Werten würden, bei Übereinstimmung der theoretischen und beobach-
teten Werte für T1, auf Abhängigkeit zwischen aufeinander-
folgenden Additionseinheiten schließen lassen. Betrachten wir die
Zufallsgröße t
]
liegen.
Die Statistik T2K überprüft die Häufigkeit des Auftretens
der Polygramme der Länge 5. Abweichungen von den theoretischen
Werten würden, bei Übereinstimmung der theoretischen und beobach-
teten Werte für T1, auf Abhängigkeit zwischen aufeinander-
folgenden Additionseinheiten schließen lassen. Betrachten wir die
Zufallsgröße t , x =
, x = 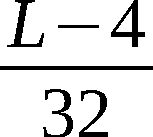 , Dt
, Dt ,
woraus bei Betrachtung der Summe NT2K unabhängiger Zufalls-
größen folgt
MT2K =
,
woraus bei Betrachtung der Summe NT2K unabhängiger Zufalls-
größen folgt
MT2K =  , δ = 1,2,3
In denen der Wert T2K mit der angegebenen Wahrscheinlichkeit
(68%, 96%, 99,7%) liegen muß.
Indem wir die Gleichberechtigung aller T2K bzgl. K berücksichtigen
und die als unabhängig ansehen, kann man den Ausdruck
, δ = 1,2,3
In denen der Wert T2K mit der angegebenen Wahrscheinlichkeit
(68%, 96%, 99,7%) liegen muß.
Indem wir die Gleichberechtigung aller T2K bzgl. K berücksichtigen
und die als unabhängig ansehen, kann man den Ausdruck
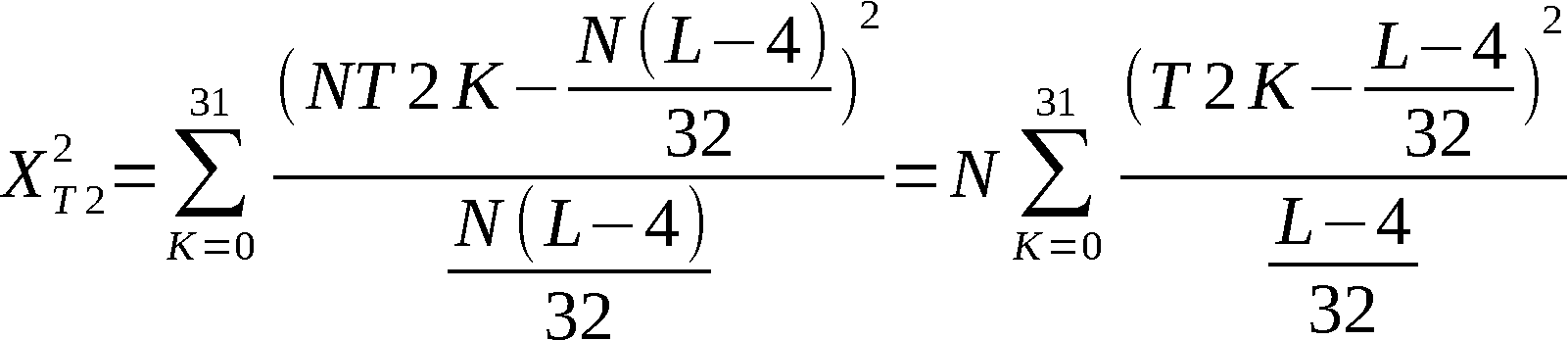 betrachten, der für N → ∞ gegen die X
betrachten, der für N → ∞ gegen die X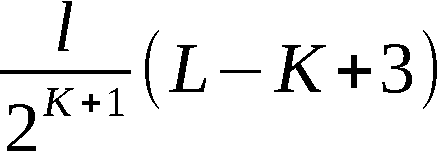 , K =
, K = 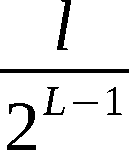 , K =
, K =  , K =
, K =  Man kann t
Man kann t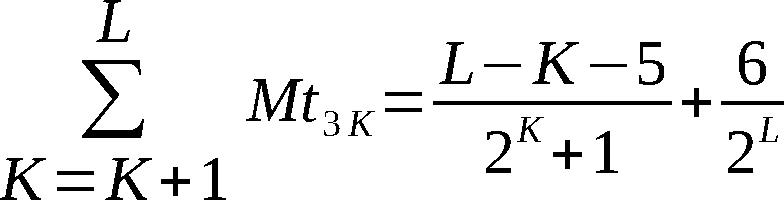 Hieraus folgt
MT30 =
Hieraus folgt
MT30 =  Wir bilden die Größe
Wir bilden die Größe
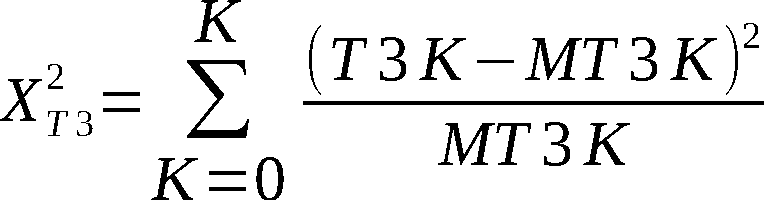 Es wird erwartet, daß sie für N → ∞ gegen die X
Es wird erwartet, daß sie für N → ∞ gegen die X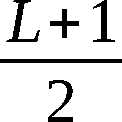 , Dt
, Dt ;
für L → ∞ nähert sich die Verteilung t
;
für L → ∞ nähert sich die Verteilung t , DT4 =
, DT4 = 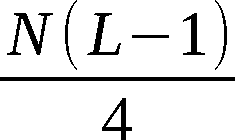 .
Entsprechend muß sich mit Wahrscheinlichkeit 68 %, 96 %, 99,7 %
der beobachtete Wert T4 in dem Intervall
.
Entsprechend muß sich mit Wahrscheinlichkeit 68 %, 96 %, 99,7 %
der beobachtete Wert T4 in dem Intervall
 , δ = 1,2,3
befinden.
Wir betrachten t
, δ = 1,2,3
befinden.
Wir betrachten t , x =
, x =  ≈ 0,1101, so ist
P[t
≈ 0,1101, so ist
P[t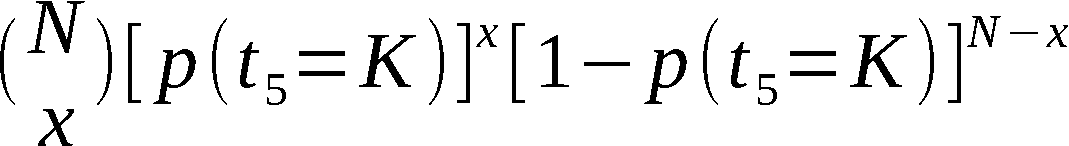 , x =
, x =  p(t
p(t ; δ = 1, 2, 3
befinden. Abweichungen würden auf Abhängigkeiten zwischen A
; δ = 1, 2, 3
befinden. Abweichungen würden auf Abhängigkeiten zwischen A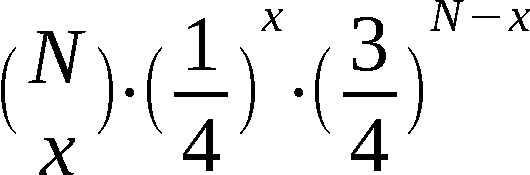 , x =
, x =  , δ = 1, 2, 3
befinden.
3.7.4. Beobachtete Resultate
Es wurden 32 Schlüssel untersucht; drunter einige
reguläre, z. B. S
, δ = 1, 2, 3
befinden.
3.7.4. Beobachtete Resultate
Es wurden 32 Schlüssel untersucht; drunter einige
reguläre, z. B. S liegt.
K
liegt.
K , T2 (1), T2 (2), T2 (3) und
, T2 (1), T2 (2), T2 (3) und 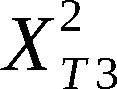 durch die in Tabelle I, N
durch die in Tabelle I, N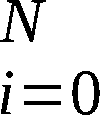 für
festes α ∈
für
festes α ∈  .
Indem man die Zerlegung von
.
Indem man die Zerlegung von  + C
+ C = 0, für i =
= 0, für i = 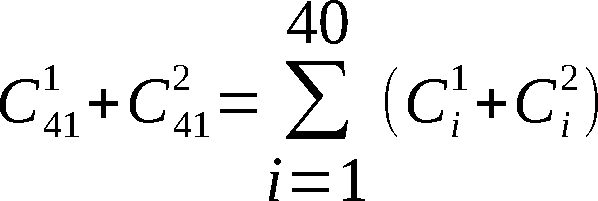 Das folgt daraus, daß das Element g
Das folgt daraus, daß das Element g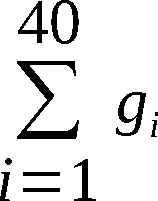 bestimmt ist.
Aus den Eigenschaften der Codesicherung I folgt (N3)
Die Summe C
bestimmt ist.
Aus den Eigenschaften der Codesicherung I folgt (N3)
Die Summe C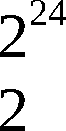 ) ≈ 2
) ≈ 2 10 BCD-Werte durchläuft, so nimmt nicht in
allen Fällen G
10 BCD-Werte durchläuft, so nimmt nicht in
allen Fällen G auch BCD-Werte an, im Mittel nur in ≈ 2/3
aller Fälle. In einem beliebigen Fall, jedoch ergeben sich
zumindest einige vereinbare Paare (G
auch BCD-Werte an, im Mittel nur in ≈ 2/3
aller Fälle. In einem beliebigen Fall, jedoch ergeben sich
zumindest einige vereinbare Paare (G für festes K und gewisse i.
Man kann notwendige Kriterien für die Erfüllung solcher
Beziehungen finden. Aber aufgrund der geringen Wahrschein-
lichkeit dieser Ereignisse und der geringen Effektivität
dieser Kriterien gelingt es faktisch weder solcher Paare
zu finden, noch sie auszunutzen.
4.2.5. Folglich: Das Dekryptieren ohne Rekonstruktion des
Schlüssels ist in der Praxis unmöglich.
4.3. Der Einfluß der Blendnachrichten auf die kryptologischen
Eigenschaften des Systems OPERATION
Bei störungsfreier Arbeit der Technik und ihrer vorschrifts-
mäßigen Bedienung unterscheiden sich die Blendnachrichten
auf dem Kanal in keiner Weise von operativen Nachrichten.
Von 2
für festes K und gewisse i.
Man kann notwendige Kriterien für die Erfüllung solcher
Beziehungen finden. Aber aufgrund der geringen Wahrschein-
lichkeit dieser Ereignisse und der geringen Effektivität
dieser Kriterien gelingt es faktisch weder solcher Paare
zu finden, noch sie auszunutzen.
4.2.5. Folglich: Das Dekryptieren ohne Rekonstruktion des
Schlüssels ist in der Praxis unmöglich.
4.3. Der Einfluß der Blendnachrichten auf die kryptologischen
Eigenschaften des Systems OPERATION
Bei störungsfreier Arbeit der Technik und ihrer vorschrifts-
mäßigen Bedienung unterscheiden sich die Blendnachrichten
auf dem Kanal in keiner Weise von operativen Nachrichten.
Von 2