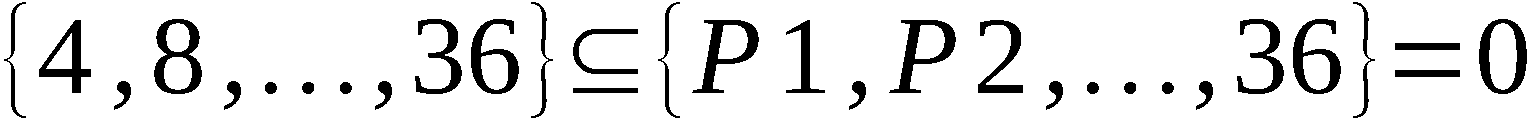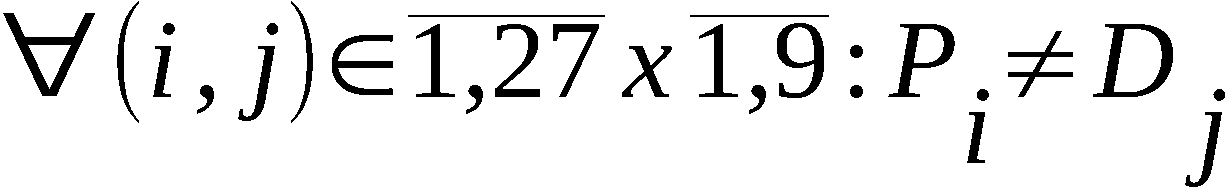T-310 Schlüsselunterlagen
BArch*1, *15, *17, *50, *59, *61, *78, *109, *129, *131, *166, *168
BArch*1, *15, *17, *59, *61, *78, *109, *129, *131, *166, *168, *215, *216, *335, *382
BArch*399, *430 - *449, *719, *725, *741
Langzeitschlüssel
Der Chiffrieralgorithmus läßt 1050 verschiedene LZS und die technische
Realisierung des Chiffrators ca. 1038 verschiedene LZS zu.
Die LZS sind nicht alle kryptologisch gut. Zur Bestimmung kryptologisch
qualitätsgerechter LZS existiert im ZCO eine Vorschrift.
Aus LZS-Klassen, deren Vertreter notwendige kryptologisch gute Eigen-
schaften besitzen werden zufällig LZS ausgewählt und weiteren theore-
tischen Untersuchungen und experimentellen Test unterzogen.
Die LZS-Klassen haben, in Abhängigkeit vom Umfang der garantierten
Eigenschaft, 1019 bis 1024 Elemente.


Abb.: Langzeitschlüssel in Folienverpackung. Sammler*119

Abb.: LSZ 21, Karte 13 in Durchlichtaufnahme. Sammler*119

Abb.: LSZ 21, Karte 14 in Durchlichtaufnahme. Sammler*119
Abteilung XI/10 Berlin, 22. Oktober 1985
Referat 102 Geheime Verschlußsache
GVS-o020
MfS-Nr. XI/596/85
04. Ausf. Bl. 01 bis 04
bestätigt:
Leiter Abteilung XI/10
Krey
Oberstleutnant
Der Langzeitschlüssel im Gerät T 310/50
1. Vorbemerkungen
1.1. Im weiteren wird abgekürzt
Langzeitschlüssel = LZS
1.2. Es ist nicht möglich, in der geforderten Kurzfassung
alle wesentlichen Aspekte des Themas ausreichend darzustellen.
Einige Aussagen sind deshalb etwas vereinfacht.
Eine ausführliche Darlegung der Problematik ist im Dokument
Kryptologische Analyse des Chiffriergerätes T 310/50
,
GVS ZCO 402/80, enthalten, insbesondere in
- Kapitel II, Punkte 1., 4.2., 4.3.;
- Gesamtzusammenfassung, Punkt 2.1.
Die dort formulierten Aussagen werden durch die Arbeitsergeb-
nisse der letzten Jahre unterstützt, einige Details würden
wir heute jedoch anders darstellen.
1.3. Bei Geräten mit internem Schlüssel basieren Aussagen
zur kryptologischen Sicherheit objektiv immer nur auf dem
erreichten Stand von Wissenschaft und Technik und subjektiv
auf
dem Grad der Umsetzung dieses Standes in dem Kollektiv,
das die Sicherheit einschätzt. Das heißt, die nachfolgenden
Aussagen können durch neue Erkenntnisse modifiziert werden
bzw. der Gegner kann zu anderen Einschätzungen als wir
gelangen.
1.4. In anderen Geräten, unter anderen Anwendungsbedingungen
kann die Rolle des LZS anders sein als bei T 310/50. Das
heißt, die nachfolgenden Aussagen sind nicht ohne weiteres
auf jedes beliebige Chiffriergerät verallgemeinbar.
2. Der Beitrag des LZS im Gerät T 310/50 zur Gewährleistung
der kryptologischen Sicherheit
Chiffrieralgorithmus und Schlüsselsystem - bestehend aus
Spruchschlüssel (SpS), Zeitschlüssel (ZS) und LZS - bilden
eine Einheit bei der Gewährleistung der kryptologischen Sicher-
heit der mit dem Gerät T 310/50 chiffrierten Sprüche. Die Eigen-
schaften des LZS beeinflussen die kryptologische Sicherheit
wesentlich. Nicht alle im Chiffrieralgorithmus möglichen LZS
sind gleich gut. Der LZS muß eine Reihe von Kriterien erfüllen,
damit hohe Sicherheit gewährleistet werden kann. Alle von uns
für den operativen Einsatz freigegebenen LZS genügen diesen
Kriterien.
Im weiteren werden in diesem Punkt stillschweigend immer
solche LZS vorausgesetzt.
Die Entwicklung des Chiffrieralgorithmus T 310 erfolgte mit
der Zielstellung, daß der ZS alleine die kryptologische Sicher-
heit garantieren soll. Das heißt in vereinfachter Form:
Bei Kenntnis sämtlicher variablen und festen Komponenten des
Chiffriergerätes und des Chiffrierverfahrens (darunter LZS,
Chiffrieralgorithmus, Chiffriergerät, Gebrauchsanweisung) - mit
Ausnahme des ZS - sowie bei fehlerfreier Arbeit des Gerätes
und dessen fehlerfreien Bedienung ist die Gewinnung von Klar-
texten aus Geheimtexten durch Dekryptierung praktisch unmöglich.
Sehr wahrscheinlich sind diese Zielstellung erfüllt.
Wir nehmen an, daß der LZS alleine ebenfalls die kryptologische
Sicherheit garantiert; daß heißt, die Aussage des vorletzten
Satzes gilt auch dann, wenn man in hier die Wörter "ZS" und
"LZS" miteinander vertauscht.
Der LZS ist somit eine zusätzliche Komponente der kryptolo-
gischen Sicherheit. Sie kommt zur Wirkung, wenn der ZS kom-
promittiert ist.
3. Kryptologische Aspekte des LZS-Wechsels
Wir fordern keine Begrenzung der Geltungsdauer und der Größe
des Schlüsselbereichs für einen LZS. Wir empfehlen, beide
Faktoren möglichst klein zu halten.
Wir werden LZS-Wechsel fordern, wenn wir im Rahmen der weite-
ren Analyse des Chiffrieralgorithmus entdecken, daß das gegen-
wärtige System der LZS-Kriterien die Sicherheit nicht gewähr-
leistet. Wir sehen bisher dafür keine Anzeichen, können diesen
Fall aber nicht ausschließen, da wesentliche Fragen, wie z. B.
äquivalente Schlüssel, immer noch ungelöst sind.
4. Operative Aspekte des LZS-Wechsels
Je kleiner ein LZS-Bereich und je kürzer die LZS-Geltungsdau-
er, um so schwerer ist es für den Gegner, einen LZS zu beschaf-
fen, und um so geringer ist der Nutzen für ihn, wenn ihm ein
LZS in die Hände fällt.
Je länger die Geltungsdauer des LZS und je größer der LZS-
Bereich, desto größer wird der Kreis derer, denen der LZS
bekannt wird.
Ist der LZS dem Gegner bekannt, so entfällt seine Wirkung als
Komponente zusätzlicher kryptologischer Sicherheit im Sinne
von Punkt 2.
Wird der LZS gewechselt, zwingen wir den Gegner, den neuen
LZS zu beschaffen, wenn er dekryptieren will, bzw. wenn er
ihm bekannt gewordene ZS nutzen will.
Das Gerät T 310/50 läßt folgende personelle Trennung zu:
- Personen, die Sprüche chiffrieren bzw. dechiffrieren, haben | Kommentar:
keine Kenntnisse über ZS und LZS | Aus heutiger Sicht die der Chiffreure
| nicht ganz korrekt. Chiffreure lesen
- Personen, die den ZS-Wechsel vornehmen, kommen nicht mit | den ZS ein, chiffrieren bzw. dechif-
Sprüchen bzw. dem LZS in Berührung | frieren. Anders bei Fernschreib-
| kräften die nur das BT/BTZ der T 310/50
- Arbeiten im Zusammenhang mit dem LZS, z. B. Funktionsüber- | bedienen. Aber beide haben keinen
prüfungen oder Austausch von LZS-Leiterplatte, erfolgt | Zugriff auf den LZS.
durch Personen, die keinen Zugang zu Sprüchen und ZS haben. | Mit dem STAN-90 war eine Reduierung der Chiffreure
| geplant - infolge eine Aufstockung der Fernschreib-
Wir befürworten LZS-Wechsel, empfehlen aber gleichzeitig | kräfte
sorgfältige Prüfung aller Umstände, insbesondere des Verhält-
nisses von Gewinn an Sicherheit einerseits und Aufwand anderer-
seits, in folgenden Situationen:
- es ist mit Sicherheit bekannt oder mit großer Wahrschein-
lichkeit anzunehmen, daß der LZS dem Gegner in die Hände
gefallen ist,
- Übergang zum Verteidigungszustand. | Kommentar 1985: Siehe Dokumentation Abt. XI,
| andere Schlußfolgerung!
5. Aufwand für einen LZS-Wechsel
Bei der Entscheidung über einen LZS-Wechsel ist der hohe
ökonomische und organisatorische Aufwand zu beachten.
(1) Der Wechsel eines LZS ist wesentlich aufwendiger als der
Wechsel eines ZS; dabei ist zu beachten, daß zum Schlüs-
selwechsel auch Nachweisführung, Funktionsüberprüfung und
anders mehr gehören.
(2) Ein LZS-Wechsel muß in allen Geräten des Schlüsslbereiches
weitgehend gleichzeitig erfolgen, anderenfalls wird die
Chiffrierarbeit ernsthaft gestört.
(3) Die Konstruktion eines LZS und die Überprüfung der gefor-
derten kryptologischen Eigenschaften erfordern mindestens
ca. 60 - 100 Stunden theoretische Arbeit und ca. 200 Stunden
Rechenzeit auf PRS 4000 und ES 1055. Im laufenden Arbeits-
prozeß werden hierfür ca. 3 Monate benötigt.
(4) Nach Informationen vom Gen. Hptm. Götz erfordert die Pro-
duktion der LZS mit der gegenwärtig möglichen Technologie
folgenden Aufwand:
Erarbeitung der Topologie für einen LZS - ca. 50 Stunden;
Aufwand für 1000 Geräte (entspricht 3000 Leiterplatten)
- Material 24 TM (davon NSW 4,5 TVM)
- Kooperation 25,5 TM
- Eigenleistung MfS (VS-Produktion) 1500 Stunden
- Produktionszeitraum 1 - 2,5 Jahre (abhängig von Beding-
ungen bei OTS als Produzent)
Stephan
Major
GVS MfS o020-XI/596/85
Blatt 5
Berlin, 13. März 1986
Ergänzung zum Dokument
Der Langzeitschlüssel im Gerät T 310/50
Nach Informationen von Genossen der Abteilung XI/1 sind
für einen LZS-Wechsel folgende weitere Aufwendungen notwendig:
(5) Bei Einsatz von Universal-Leiterplatten sind für einen
Satz LZS (für ein Gerät T 310/50) folgende Aufwendungen
erforderlich:
- Materialkosten 76,80 Mark
- zeitlicher Aufwand für Handverdrahtung ca. 4 Std.
(6) Die Umprogrammierung des Prüfrechners PR 310/2 und die
Änderung der Dokumentation machen im wesentlichen folgende
Arbeiten erforderlich:
- Bereitstellung erforderlicher Daten durch Abt. XI/10,
vgl. (3)
- Berechnung, Programmierung, Erprobung des Daten-EPROM
- Bereitstellung der erforderlichen Anzahl EPROM
- Erarbeitung/Kontrolle des Brückenplanes sowie für Buch 5
der Austauschblätter
- Herstellung der erforderlichen Auflage o. g. Dokumentation
Arbeitszeitaufwand ca. 4 bis 8 Wochen
Stephan
Major
Abteilung XI/1 Berlin, 19. Juni 1986
Geheime Verschlußsache
GVS-o020
MfS-Nr. XI/311/86
01. Ausf. Bl.01 bis 04
Betrachtungen zum Problem
Langzeitschlüsselwechsel der Geräte-
systeme T 310/50
(1) Bei den Betrachtungen bezüglich des Wechsels der Langzeitschlüssel des
Gerätesystems T 310/50 müssen auch die Systeme T 310/51 und SKS V/1
berücksichtigt werden, da deren Grundaufbau analog ist.
(2) Der Langzeitschlüssel eines Systems T 310/50 besteht aus drei Leiter-
platten der Größe 95 x 47,5 mm mit eigener Topologie.
Die Produktion dieser Langzeitschlüssel erfordert derzeit einen tech-
nologischen Durchlauf in der Abteilung XI, bei OTS und in zwei Indu-
striebetrieben in Kooperationsarbeit.
Material- und Kooperationskosten ohne Eigenleistung betragen für
eine Leiterplatte ca. 18,-- M.
Für 3461 Gerätesysteme T 310/50 (ca. 10 400 Leiterplatten) betragen
o. g. Kosten ca. 187 TM, deren Produktionszeitraum beläuft sich auf
ca. sechs Jahre, bei Anwendung besonderer Maßnahmen ca. zwei Jahre.
Die Höhe der Eigenleistung ist beträchtlich.
(3) Der Langzeitschlüssel eines Gerätesystems T 310/51 besteht ebenfalls
aus drei Leiterplatten der Größe 95 x 47,5 mm wahlweise mit eigener
Topologie oder Handverdrahtung.
Die Produktion dieser Langzeitschlüssel für ca. 50 Systeme erfordert
ebenfalls den o. g. technologischen Durchlauf, bei Handverdrahtung
die Kooperation mit dem Hersteller der Systeme (Lieferung von Uni-
leiterplatten) und einen technologischen Durchlauf in der Abteilung XI.
(4) Der Langzeitschlüssel eines Gerätesystems SKS V/1 in Normalausstattung
umfaßt 32 handverdrahtete Unileiterplatten der Größe 170 x 95 mm.
Die Gesamtmenge der in den Systemen eingesetzten Langzeitschlüssel-
leiterplatten ist fast 550.
Es gibt sechs Langzeitschlüsselbereiche, untergliedert nach Ländern.
Die Leiterplatten für einen vollständigen Wechsel sind in Abteilung XI
vorrätig und für einen Langzeitschlüsselbereich wurde eine Reserve
produziert.
(5) Außer der theoretischen Arbeit und der für die technische Realisierung
sind im Falle des Wechsels der Langzeitschlüssel bei den Systemen
T 310/50 und T 310/51 Leistungen für eine Umprogrammierung der Prüf-
rechner und eine Änderung der Dokumentation zu erbringen.
Bei Systemen SKS V/1 sind eine neue Variante Prüflochkarten zu er-
arbeiten und zu produzieren und ebenfalls die Dokumentation zu
ändern.
(6) Es ist vorgesehen, das Verfügungsrecht zu den Langzeitschlüsseln der
Systeme SKS V/1 an Abteilung III zu übertragen.
(7) Die komplizierte und enge Vermaschung aller mit den Gerätesysteme
T 310/50 organisierten Chiffrierverbindungen der einzelnen Chiffirer-
dienste auf allen Ebenen bedingt, daß nur ein Langzeitschlüssel-Bereich
gebildet werden kann.
(Vergl. Diskussionsmaterial Einsatz Langzeitschlüssel T 310/50
,
GVS ZCO-208/86)
(8) Separate Langzeitschlüsselbereiche sollten nur für in sich abgeschlos-
sene Nachrichtensystem geschaffen werden. Dafür eignet sich das Füh-
rungssystem FÜ-445 (T 310/51).
(9) Es ist zu prüfen, ob eine Neuauflage des derzeitigen operativen Lang-
zeitschlüssels bis zur Höhe der noch zu produzierenden Gerätesysteme
zweckmäßig ist. (Die Produktion der Langzeitschlüssel für 3000 Geräte-
systeme ist abgeschlossen. Der Reserve-Langzeitschlüssel ist für 1500
System produziert.)
Um die Aufwendungen dafür in Grenzen zu halten, sollte diese Menge
Langzeitschlüssel handverdrahtet auf Unileiterplatten gefertigt wer-
den (Materialkosten ca. 12 TM, eigene Arbeitszeit ca. 500 Std. - 1 VbE
ca 2 - 3 Monate).
(10) Die Aktion Wechsel der Langzeitschlüssel
ist in einer Konzeption
detailliert so vorzubereiten, daß mit den vorhandenen Kräften und
Mitteln der Wechselzeitraum sehr klein und damit der Ausfall von
Chiffrierverbindungen, auch hinsichtlich ihrer Vermaschungen, gering
gehalten wird.
(11) Für den Fall eines Wechsels des Langzeitschlüssels ist zu prüfen, ob
eine zweite Langzeitschlüsselreserve für alle Gerätesysteme T 310/50
zu produzieren ist.
(12) Bei einer geplanten Produktion der Langzeitschlüssel bis nach 1990 muß
gesichert werde, daß die technologischen Bedingungen in den koopera-
tiven Industriebetreiben erhalten bleiben oder daß Alternativlösungen
angeboten werden.
(13) Um der Möglichkeit der Nichtgewährleistung der Sicherheit der Lang-
zeitschlüssel-Kriterien durch weitere Analysen vorzubeugen, sollte,
falls erforderlich, die zweite Langzeitschlüssel- Reserve handver-
drahtet auf Unileiterplatten hergestellt werden.
Dafür müssen Materialkosten von ca. 265 TM und eigene Arbeitszeit von
ca. 10 400 Std. (zehn VbE ca. 1/2 Jahr) geplant werden.
Die Einlagerung einer entsprechenden Anzahl von Unileiterplatten ist
auch in Verbindung mit Pkt. (12) zu sehen.
(14) Ein zyklischer Wechsel der Langzeitschlüssel im Gerätesystem T 310/50
ist aus kryptologischen Gründen nicht zwingend erforderlich, wird aber
in operativer Hinsicht befürwortet nach gründlicher aller da-
mit in Zusammenhang stehenden Faktoren (Vergl. Der Langzeitschlüssel
im Gerät T 310/50
, GVS XI/596/85, Pkt. 2 und Pkt. 5(1) bis (6)).
Aus ökonomischen Gründen erscheint ein zyklischer Wechsel der Langzeit-
schlüssel nicht gerechtfertigt (vergl. Pkt. (2) und (5) dieser Doku-
ments).
Ein Wechsel des derzeitig operativen Langzeitschlüssels sollte, wenn
die operative Notwendigkeit besteht, erst nach Beendigung der Produktion
der Geräte T 310/50 und Bereitstellung des 1. Reserve-Langzeitschlüssels
durchgeführt werden (ca. 1992).
(15) Die gegenwärtig betrachteten operativen Gesichtspunkte, die einen
zyklischen Wechsel des Langzeitschlüssels begründen, sollte durch
organisatorische und andere Maßnahmen entschärft werden, z. B.:
- zusätzliche Sicherungsmaßnahmen für Langzeitschlüssel im
Gerät, die einen unbefugten Zugriff erkennen lassen
- Einschränkung des Personenkreises, welche Zugang zum Lang-
zeitschlüssel haben (Instandsetzung)
- Reduzierung der Informationen zum Langzeitschlüssel auf
ein Minimum (Einziehen der Bp Langzeitschlüssel)
Büttner
Oberstleutnant
Referat 11 Berlin, 22. 12. 75
Geheime Verschlußsache
MfS 020 Nr. XI/127/76
01. Ausf. 9 Blatt
Klasse ALPHA: Langzeitschlüsselverzeichnis
In diesem Dokument werden alle LZS erfaßt, die in irgendeiner Form
wirksam wurden bzw. werden.
Bezeichnungen gemäß Beschreibung Klasse ALPHA
, 05. 08. 75,
GVS 415/75.
Die Angaben zu jedem LZS sind auf einem gesonderten Blatt dargestellt.
Die hier benutzte Numerierung der LZS ist nur für den internen Gebrauch
als Unterscheidungsmerkmal gedacht.
Erfaßt werden die LZS-Komponenten P, R, Uo, α - soweit fest-
gelegt wurden in folgender Form:
P in der Form P = (P1, P2, P3, …, P27)
R in der Form R = (R1, R2, R3, …, R9)
Uo in der Form Uo = (Uo1, Uo2, Uo3, …, Uo27)
α in der Form α = α
Weiterhin sind exakt und konkret alle wesentlichen Charakteristika
der LZS zu erfassen, insbesondere:
Zeitraum der Erarbeitung, kryptologische Qualität, EDV-Untersuchungen,
Anwendungsgebiete, technische Realisierung, Verweise auf Unterlagen
mit weiteren Angaben, Besonderheiten.
Ergänzungen und Änderungen werden in angemessener Form nachgetragen.
Blattweise unterschrieben je zwei Genossen für die Richtigkeit von
(P, R, Uo, α) und der Angaben zur kryptologischen Qualität.
Nachtrag zur Einleitung des LZS-V
Ebenfalls in diesem Dokument erfaßt und in die lfd. Numerierung
einbezogen werden alle LZS (P, D, α) der Realisierung von ALPHA
im Chiffrieralgorithmus T 310 gemäß GVS 190/79, die in irgend-
einer Form wirksam wurden bzw. werden; einschließlich solcher,
die nur der Definition (Punkt 2. der GVS) ohne die Einschränkungen
(Punkt 4. der GVS) genügen.
Darstellung gemäß GVS 190/79:
P = (P1, P2, …, P27)
D = (D1, D2, …, D9)
α = α
Darstellung gemäß 1990:
P = (P1, P2, …, P27)
D = (D1, D2, …, D9)
T = (T1, T2, …, T9)
α = α
Die Langzeitschlüsselklasse KT1 und KT2:
Die Klasse KT1 stelle eine für die 36-Bit-Variante (T310-50)
verallgemeinerte Form der in /3/ angegebenen Klasse K2 der 27-Bit-
Variante (SKS V/1) dar; sie enthält nur LZS mit der Eigenschaft
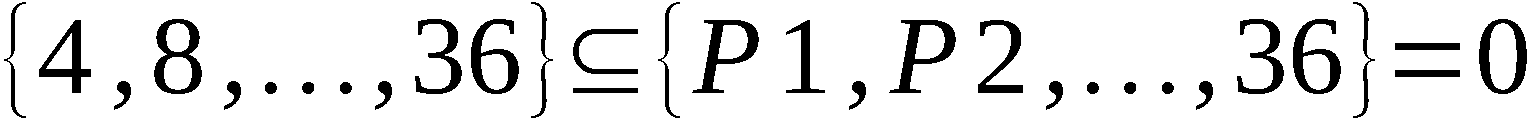
D1 = 0, {D2, D3, …, D9} \ {4, 8, …, 36} = 0
und ist durch eine Doppelbelegung
gewisser Komponenten
aus u4, u8, …, u36 als uDi und als Argumente einiger
T10-i gekennzeichnet.
Die Klasse KT2 zeichnet sich durch Einfachbelegung
aus,
d. h. für LZS der Klasse KT2 ist
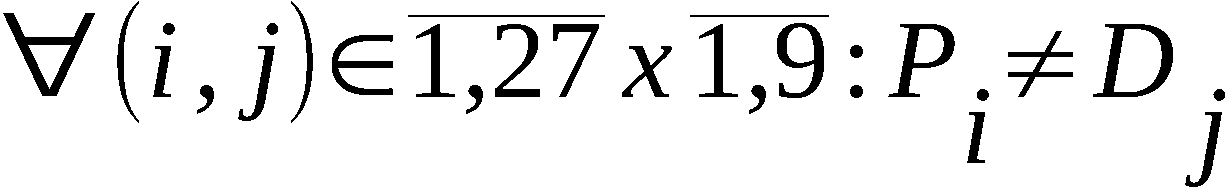
erfüllt. Die Klasse KT2 unterscheidet sich wesentlich von den
in /3/ angegebenen Klassen und besitzt kein entsprechende
Analogien.
/3/ Ergebniss der Untersuchungen der Chiffrieralgorithmen - Klasse ALPHA
GVS ZCO-198/77
Mittels des DV-Projekt PRÜFUNG-36, Programm P541 01/A,B,C,
erfolgte die Überprüfung der Eigenschaften des LZS.
Abteilung XI/1 Berlin, 30. April 1984
Geheime Verschlußsache
GVS-o020
MfS-Nr. XI/376/84
02. Ausf. Bl. 01 bis 04
Operative T 310-LZS: Schnittstelle mathematische
Darstellung - technische Realisierung
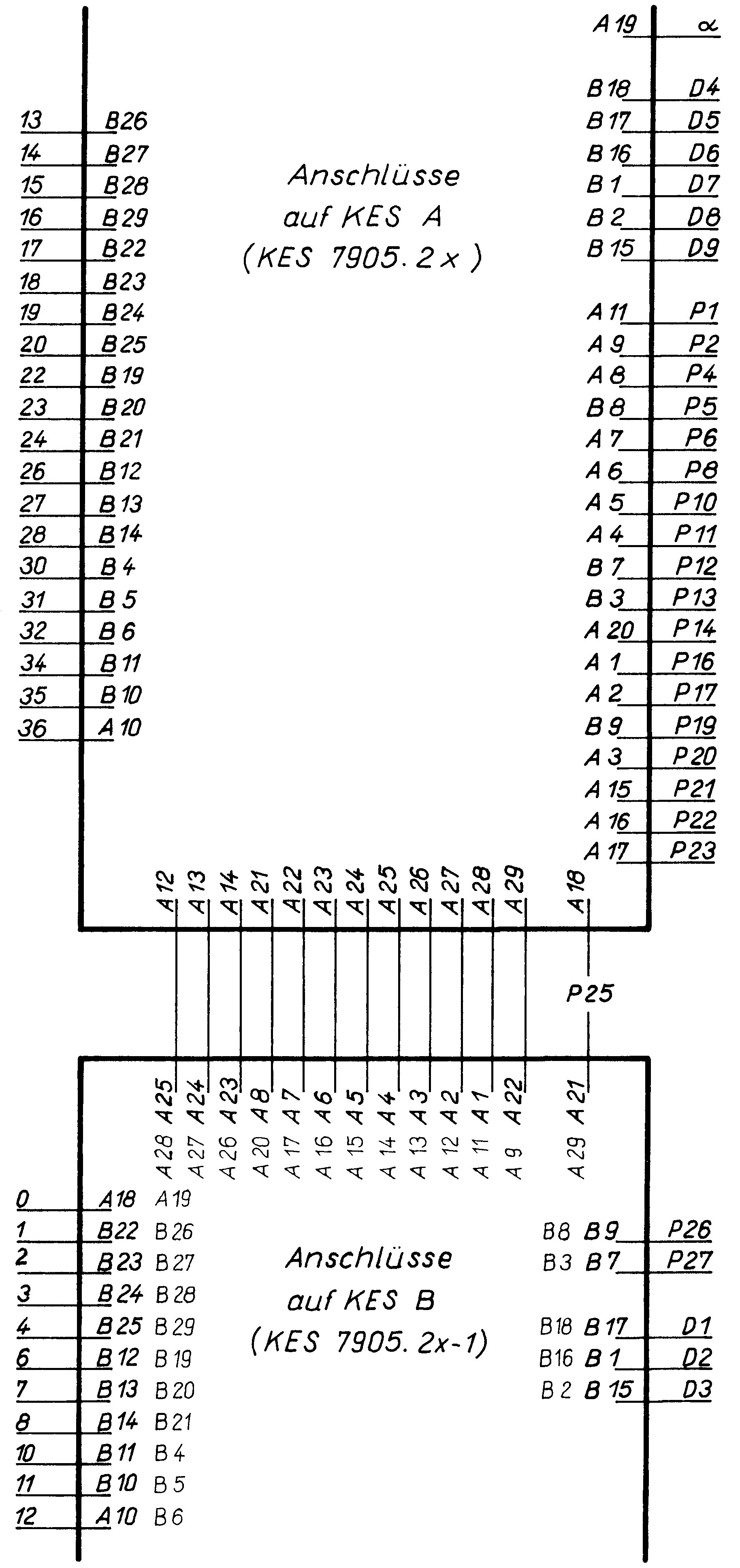
Abb.: Realisierungshilfe LZS
Die mathematische Beschreibung oder der Brückenplan des Langzeitschlüssels
LZS 1 3 4 5 6 7 8 10 14 15 16 17 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 ?? Untersuchung
Beispiele für einen Brückenplan 17, 21, 26, 30, 31
Leseweise der P Folge, am Beispiel des LSZ-31:
P = (7, 4, 33, 30, 18, 36, 5, 35, 9, 16, 23, 26, 32,
12, 21, 1, 13, 25, 20, 8, 24, 15, 22, 29, 10, 28, 6)
D = (0, 16, 4, 24, 12, 28, 32, 36, 20)
α = (2)
Z1 = (S2, U7, U4, U33, U30, U18); T31 = T21 XOR U36
Z2 = (U5, U35, U9, U16, U23, U26); T51 = T41 XOR U32
Z3 = (U12, U21, U1, U13, U25, U20); T71 = T61 XOR U8
Z4 = (U24, U15, U22, U29, U10, U28); T91 = T81 XOR U6
Die unterstrichenen U-Vektoren sind konstant, siehe Beschreibung
Komplizierungseinheit.
In der Darstellung der P-Folge wird S2 nicht aufgeführt.
Leseweise der D Folge:
T92 = S1 entspricht der Null
T82 = U16, T72 = U4, T62 = U24, T52 = U12, T42 = U28, T32 = U32, T22 = U36, T12 = U20
d = 2 bedeutet das D-W, die Wurmfolgen, aus dem Vektor U2 bezogen werden.
Die Bezeichner R, Uo ist für die Beschreibung der Vektoren für die SKS V/1.
Uo ist der Start U-Vektor und R stellt die Tx2 Verknüpfung zu den U-Vektoren dar.
Der Langzeitschlüssel 1: (1973)
P = (22, 7, 18, 2, 16, 27, 23, 3, 14, 1, 13, 25, 24, 12,
17, 4, 11, 9, 26, 15, 10, 19, 8, 5, 20, 6, 21)
R = (8, 5, 6, 2, 9, 4, 7, 3, 1)
Uo = (000 000 011 011 111 111 100 000 000)
α = 1
Mit diesem P und R ist die Abbildung φ eineindeutig (im Sinne GVS 747/73,
IV, § 1, 2,) und effektiv (im Sinne GVS ZCO-198/77)
Experimentell wurde ermittelt:
- die durch Uo bestimmte Zustandsklasse (im Sinne GVS 747/73, IV, § 1, 4,)
enthält über 92 Millionen Elemente; vgl. GVS 76/74, 3.1;
- Die Additionsreihen besitzen gute statistische Eigenschaften vgl. GVS
76/74, 3.7., GVS 747/73 Blatt 81 ff.
// Dieser Schlüssel ist bekannt im: IfR, Steremat, Abt.F, Abt XIII, sowj. ZCO
// Der LZS wurde bzw. wird benutzt als Beispiel in der SKS-Analyse GVS 747/73,
// in SKS V/1-Mustergeräten (AF 2, K5), einschließlich Kanalerprobung der
// Mustergeräte, im Produktionsbetrieb und beim Anwender für Prüfzwecke.
// Der LZS darf nicht im Chiffrierbetrieb benutzt werden.
Der Langzeitschlüssel 3: (1975)
P = (10, 17, 2, 18, 13, 1, 24, 23, 26, 12, 21, 25, 3,
5, 22, 20, 15, 16, 14, 27, 4, 9, 6, 19, 8, 7, 11)
R = (5, 9, 6, 3, 7, 4, 2, 8, 1)
Aufgrund eines Rechenfehlers bei der Erarbeitung des LZS ist die Abbildung φ
nicht eindeutig.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 4: (1975)
P = (5, 23, 8, 18, 13, 22, 15, 7, 16, 25, 3, 10, 27,
21, 11, 1, 4, 12, 17, 24, 2, 20, 6, 9, 26, 19, 14)
R = (7, 6, 2, 8, 3, 5, 9, 4, 1)
Uo = (111 111 111 111 000 000 111 000 111)
Die Abbildung φ ist eineindeutig und effektiv.
Die durch Uo bestimmte Zustandsklasse enthält über 10 Millionen Elemente.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 5: (1975)
P = (7, 21, 17, 19, 25, 27, 4, 5, 16, 3, 23, 11, 9, 8,
18, 1, 10, 20, 12, 24, 14, 26, 13, 15, 22, 2, 6)
R = (3, 7, 9, 2, 4, 5, 8, 6, 1)
Uo = (111 000 111 111 000 111 111 000 111)
Die Abbildung φ ist eineindeutig und effektiv.
Die durch Uo bestimmte Zustandsklasse enthält über 55 Millionen Elemente.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 6: (1975)
P = (3, 7, 14, 15, 20, 5, 6, 12, 22, 21, 8, 2, 18, 1,
4, 24, 10, 11, 16, 23, 9, 13, 19, 26, 17, 25, 27)
R = (6, 5, 8, 7, 9, 4, 2, 3, 1)
Uo = (111 000 111 111 000 111 000 111 111)
Die Abbildung φ ist eineindeutig und effektiv.
Die durch Uo bestimmte Zustandsklasse enthält über 21 Millionen Elemente.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 7: (1975)
P = (5, 11, 7, 6, 9, 13, 18, 21, 23, 12, 14, 22, 3, 15,
8, 19, 26, 17, 25, 4, 10, 24, 2, 16, 20, 1, 27)
R = (3, 8, 7, 2, 6, 9, 4, 5, 1)
Uo = (011 100 000 110 001 110 000 010 110)
α = 1
Die Abbildung φ ist eineindeutig und effektiv.
Die durch Uo bestimmte Zustandsklasse enthält über 115 Millionen Elemente.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 8: (1976)
P = (19, 3, 16, 8, 9, 25, 13, 15, 10, 21, 12, 14, 6, 18,
2, 20, 4, 1, 17, 22, 11, 24, 5, 26, 23, 7, 27)
R = (2, 8, 6, 3, 7, 9, 4, 5, 1)
Uo = (111 000 111 111 000 111 000 111 000)
α = 1
Die Abbildung φ ist eineindeutig und effektiv.
Die durch Uo bestimmte Zustandsklasse enthält über 61 Millionen Elemente.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 10: (1977)
P = (24, 4, 21, 7, 11, 16, 23, 1, 6, 9, 3, 2, 12, 18,
19, 22, 26, 25, 20, 17, 5, 8, 10, 14, 13, 15, 27)
R = (9, 3, 4, 5, 7, 6, 8, 2, 1)
Die Abbildung φ ist eineindeutig und effektiv.
Dieser Schlüssel ist speziell zur Testung des Programmes S2TSTC
(Projekt PRUEFUNG) konstruiert. die reduzierte Menge M'
besitzt nur 29 Zustände besitzen.
// Dieser Schlüssel ist bekannt in: Abt XIII
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 14: (1979)
P = (24, 34, 33, 32, 14, 4, 5, 28, 9, 26, 27, 18, 36, 16,
21, 15, 20, 25, 35, 8, 1, 6, 23, 29, 19, 12, 13)
D = (0, 28, 24, 12, 16, 32, 36, 4, 20)
α = 30
Der LZS genügt der T 310-Algorithmus-Definition, GVS 190/79,
einschließlich dort angegebener Einschränkungen. Er ist Ele-
ment der Klasse KT 1, vgl. GVS 553/80. Er besitzt die Eigen-
schaften:
- die Abbildung φ(p) ist eineindeutig für alle p,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 15: (1979)
P = (15, 13, 33, 34, 6, 8, 5, 3, 9, 18, 14, 22, 28, 30,
21, 31, 7, 25, 26, 16, 27, 11, 23, 29, 19, 1, 36)
D = (0, 4, 17, 12, 35, 32, 2, 24, 20)
α = 10
Der LZS genügt der T 310-Algorithmus-Definition, GVS 190/79,
einschließlich dort angegebener Einschränkungen. Er ist Ele-
ment der Klasse KT 2, vgl. GVS 553/80. Er besitzt die Eigen-
schaften:
- die Abbildung φ(p) ist eineindeutig für alle p,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Der LZS wird nicht benutzt.
// Der operative Einsatz ist verboten!
Der Langzeitschlüssel 16: (1979)
P = (14, 19, 33, 18, 23, 15, 5, 6, 9, 2, 34, 1, 30, 11,
21, 3, 22, 25, 17, 7, 32, 10, 27, 29, 26, 35, 13)
D = (0, 35, 19, 23, 27, 11, 3, 15, 31)
α = 18
Der LZS genügt der T 310-Algorithmus-Definition, GVS 190/79,
einschließlich dort angegebener Einschränkungen.
Gleichzeitig realisiert er die sogenannte 27-Bit-Variante
(ALPHA-Definition, GVS 415/75). In dieser Variante gilt:
- die Abbildung φ(p) ist eineindeutig für alle p,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Dieser Schlüssel ist für die K4-Mustergeräte T-310/50
// für die operative Erprobung zugelassen!
// 1984 ist dieser Langzeitschlüssel auch für die
// Erprobung der T-310/51 zugelassen worden.
Der Langzeitschlüssel 17: (1979)
P = (22, 23, 33, 11, 26, 12, 5, 4, 9, 3, 2, 1, 19, 10,
21, 8, 7, 25, 6, 35, 32, 31, 30, 29, 17, 17, 34)
D = (0, 4, 8, 12, 16, 20, 24, 28, 32)
α = 36
Dieser Schlüssel ist für ausschließlich für die technische
Prüfung der T-310 im IfR und Steremat Berlin vorgesehen. Deshalb wurde ein Widerspruch
zur T 310-Algorithmusdefinition, GVS 190/79, zugelassen
(P25 = P26 = 17).
// Stand 1982: der operative Einsatz des LZS 17 ist streng verboten!
// Stand 198x:
// Dieser Schlüssel ist wie o.g. nur für die Prüfung der T-310
// zugelassen, er wurde nie auf kryptologische Sicherheit geprüft.
// Auf KES 7905.03 und auf KES 7905.04 realisiert.
// Dieser Schlüssel ist bekannt im IfR und Steremat.
Der Brückenplan aus dem Stromlaufplan, Buch 6:
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A13 A14 A15 A16 A17 A18 A20 A22 A25 A26 A27 A28 A29 B1 B2 B6 B8 B16 B17 B25
LZ der Karte 1 = 2: A27 A26 B10 A22 A23 A24 A14 A13 B20 A19 B19 B11 B6 B5 B4 B22 A28 B7 B9 B18 B21 B14 B15 B12 B25 B29 B3
LZ der Karte 3: A26 B4 B2 B20 B19 B16 B28 B27 B18 B26 B6 B5 B3 B8 B21 B29
Der Brückenplan aus dem Dokument GVS B 253-30/79, B 253-31/79:
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16 A17 A18 A19 A20 A21 A22 A24 A25 A26 A27 A28 A29 B1 B2 B3 B6 B8 B15 B16 B17
LZ der Karte 1 = 2: A27 A26 B10 A22 A23 A24 A14 A13 B20 A19 B19 B11 B1 B5 B4 B22 A28 B7 B9 B18 B21 B14 B24 B15 B12 B25 B29
LZ der Karte 3: B11 B1 B13 B12 B15 B24 B23 B22 A26 A22 B4 B2 B20 B19 B16 B28 B27 B17 B18 B26 B9 A23 B10 B7 B6 B5 B3 B8 B14 B21 B25 B29
Änderung entspechend K5, 15.10.1982.
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16 A17 A18 A19 A20 A21 A22 A24 A25 A26 A27 A28 A29 B1 B2 B3 B6 B8 B14 B15 B16 B17
LZ der Karte 1 = 2: A27 A26 B10 A22 A23 A24 A14 A13 B20 A19 B19 B11 B6 B5 B4 B22 A28 B7 B9 B18 B14 B24 B15 B12 B21 B25 B29
LZ der Karte 3: B11 B14 B13 B12 B1 B24 B23 B22 A26 A22 B4 B2 B20 B19 B16 B28 B27 B17 B18 B26 B9 A23 B10 B7 B6 B5 B3 B8 B25 B21 B15 B29
Der Langzeitschlüssel 19: (1979)
P = (22, 19, 3, 1, 6, 21, 17, 16, 8, 11, 2, 20, 24, 9,
23, 10, 14, 26, 15, 27, 25, 7, 18, 5, 12, 13, 4)
R = (4, 8, 9, 6, 7, 5, 2, 3, 1)
Uo = (010 111 001 100 010 000 101 010 000)
α = 1
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär,
- die Gruppe G enthält alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Für den operativen Einsatz freigegeben
Der Langzeitschlüssel 20: (1980)
P = (18, 20, 15, 21, 22, 6, 17, 11, 19, 2, 23, 26, 13, 1,
10, 9, 12, 16, 7, 27, 24, 25, 14, 5, 3, 8, 4)
R = (4, 3, 7, 5, 9, 6, 8, 2, 1)
Uo = (000 010 011 101 011 111 011 010 001)
α = 27
Der LZS besitzt die Eigenschaften:
- (P, R) ∈ K2,
- die Gruppe G ist transitiv,
- die Gruppe G ist imprimitiv (!),
- die Automorphismengruppe Aut A ist trivial.
// Für operative Zwecke ist er verboten!
Der Langzeitschlüssel 21: (1981)
P = (36, 4, 33, 11, 1, 20, 5, 26, 9, 24, 32, 7, 12, 2,
21, 3, 28, 25, 34, 8, 31, 13, 18, 29, 16, 19, 6)
D = (0, 24, 36, 4, 16, 28, 12, 20, 32)
α = 1
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
Die theoretischen und experimentellen (z. B. Äquivalenzen,
statistische Eigenschaften, Wirksamkeit der Schlüsselelemente)
Untersuchungen unterstützen die Hypothese, daß der T 310-
Algorithmus mit diesem LZS gute kryptologische Eigenschaften
besitzt.
// Für den Einsatz freigegeben
Beschrieben als vollständigen Brückenplan:
7905.13 und 7905.14
| LSZ-21 | Karte-13 |
| von | B | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| nach | B | - | - | 19 | - | - | - | 12 | - | - | - | - | 7 | - | - | - | - | - | - | 3 | - | - | - | - | - | - | - | - | - | - |
| A | 8 | 11 | - | - | 12 | 17 | - | 15 | 5 | 2 | - | - | 3 | 6 | 1 | 20 | 18 | 19 | - | 13 | 16 | 23 | 24 | 25 | 4 | 26 | 27 | 28 | 14 |
| |
| von | A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| nach | A | - | - | - | - | - | - | 10 | - | - | 7 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| B | 15 | 10 | 13 | 25 | 9 | 14 | - | 1 | - | - | 2 | 5 | 20 | 29 | 8 | 21 | 6 | 17 | 18 | 16 | - | - | 22 | 23 | 24 | 26 | 27 | 28 | - |
| |
| LZS-21 | Karte-14 |
| von | B | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| nach | B | 3 | 25 | 1 | - | - | 15 | - | - | 11 | - | 9 | - | - | 16 | 6 | 14 | 29 | - | - | - | - | - | - | - | 2 | - | - | - | 17 |
| A | 22 | 7 | 22 | - | 15 | 4 | 26 | 14 | - | - | - | 6 | - | 2 | 4 | 2 | 18 | 9 | - | - | 5 | - | 17 | 24 | 7 | 16 | - | - | 18 |
| A | - | - | - | - | - | - | - | 19 | - | - | - | - | - | - | - | - | - | 25 | - | - | 21 | - | - | - | - | - | - | - | - |
| |
| von | A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| nach | A | 12 | - | 23 | | 21 | - | - | 27 | 25 | 11 | 10 | 1 | 20 | 19 | - | - | - | - | 14 | 13 | 5 | - | 3 | - | 9 | - | 8 | 10 | - |
| A | - | - | - | - | - | - | - | - | - | 28 | 28 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 11 | - |
| B | - | 14 | - | 6 | 21 | 12 | 2 | - | 18 | - | - | - | - | 8 | 5 | 26 | 23 | 17 | 8 | - | 21 | 1 | - | 24 | 18 | 7 | - | - | - |
| B | - | 16 | - | 15 | - | - | 25 | - | - | - | - | - | - | - | - | - | - | 29 | - | - | - | 3 | - | - | - | - | - | - | - |
Der Langzeitschlüssel 22: (1980)
P = (14, 3, 7, 9, 26, 19, 25, 21 ,12, 1, 22, 24, 6, 5,
16, 17, 8, 11, 15, 4, 10, 20, 23, 2, 18, 13, 27)
R = (4, 9, 8, 3, 6, 7, 2, 5, 1)
Uo = (000 111 001 101 001 011 100 001 110)
α = 19
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Für den Einsatz freigegeben
Der Langzeitschlüssel 23: (1981)
P = (23, 7, 12, 18, 24, 9, 13, 1, 20, 14, 16, 22, 19,
25, 3, 15, 17, 5, 10, 27, 26, 6, 4, 11, 8, 21, 2)
R = (7, 4, 6, 8, 2, 3, 9, 5, 1)
Uo = (001 001 001 111 100 011 111 000 010)
α = 17
Der LZS besitzt die Eigenschaften:
- (P, R) ∈ K2,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Für den Einsatz freigegeben
Der Langzeitschlüssel 24: (1981)
P = (9, 18, 2, 4, 17, 1, 3, 24, 6, 7, 8, 5, 15, 21, 11,
14, 25, 10, 26, 13, 19, 20, 22, 23, 16, 12, 27)
R = (8, 2, 3, 6, 7, 5, 4, 9, 1)
(P, R) wurden zur Testung von Programmen konstruiert.
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär, (P, R) ∈ K1,
- die Gruppe G (P, R) ist intransitiv!,
// Dieser Langzeitschlüssel ist für die Erprobung von Programmen konstruiert.
// Für den Einsatz ist er verboten.
Der Langzeitschlüssel 25: (1977)
P = (21, 1, 24, 23, 2, 16, 5, 6, 8, 3, 11, 9, 12, 10,
14, 18, 20, 25, 26, 17, 15, 4, 13, 19, 7, 22, 27)
R = (9, 3, 4, 5, 7, 6, 8, 2, 1)
(P, R) wurden zur Testung von Programmen konstruiert und sind das
erste Beispiel für die Konstruktion der Transitivität der
Gruppe G(P, R).
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär, (P, R) ∈ K1,
- die Gruppe G (P, R) ist die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial,
- bzgl. φ(0,0,1) wurde die vollständige Zyklenstruktur berechnet.
// Dieser Langzeitschlüssel ist für die Erprobung von Programmen konstruiert.
// Für den Einsatz ist er verboten. Der LZS 25, 27 und 28 ist in Abt. XIII bekannt.
Der Langzeitschlüssel 26: (1981)
Beschrieben als Brückenplan:
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A13 A14 A15 A16 A17 A18 A19 A20 A22 A23 A24 A25 A26 A27 A28 B1 B2 B3 B5 B6 B7 B9 B15 B17
LZ der Karte 1 = 2: B26 B20 A10 B24 A12 B10 B2 B15 A14 A22 B1 A19 B17 B28 B12 B13 A21 B16 B9 B6 B3 B25 B8 B18 B23 B14 B29 B21
LZ der Karte 3: B9 B1 B14 B13 A24 B8 B16 B21 B17 B18 B20 B15 B24 B2 B6 B28 B29 B5 B10 B25
P = (8, 4, 33, 16, 31, 20, 5, 35, 9, 3, 19, 18, 12, 7,
21, 13, 23, 25, 28, 36, 24, 15, 26, 29, 27, 32, 11)
D = (0, 28, 4, 32, 24, 8, 12, 20, 16)
α = 4
Der LZS genügt der T 310-Algorithmus-Definition, GVS 190/79,
Punkte 2. und 4.
Der LZS besitzt die Eigenschaften:
- (P, D, 4) ∈ K1,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial,
Die theoretischen und experimentellen Untersuchungen (z. B.
Äquivalenzen, statistische Eigenschaften, Wirksamkeit der
Schlüsselelemente, Perioden) unterstützen die Hypothese, daß
der T 310-Algorithmus mit diesem LZS gute kryptologische Eigen-
schaften besitzt.
// Für den Einsatz in der T-310 freigegeben.
// Auf KES 7905.17 und auf KES 7905.18 realisiert.
Der Langzeitschlüssel 27: (1982)
P = (10, 21, 18, 4, 5, 8, 16, 12, 6, 24, 2, 7, 3, 25,
17, 26, 9, 14, 22, 1, 20, 11, 19, 15, 13, 23, 27)
R = (8, 3, 5, 2, 4, 6, 7, 9, 1)
(P, R) wurden auf der Grundlage der in GVS 300/82 dargelegten Theorie so
konstruiert, daß G(P, R) eine transitive Gruppe ist.
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär, (P,R) ∈ K1,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Dieser Langzeitschlüssel ist für die Erprobung von Programmen konstruiert.
// Für den Einsatz ist er verboten. Der LZS 25, 27 und 28 ist in Abt. XIII bekannt.
Der Langzeitschlüssel 28: (1982)
P = (21, 8, 11, 15, 5, 1, 19, 24, 12, 14, 17, 6, 3, 10,
26, 13, 25, 22, 9, 16, 2, 18, 20, 23, 7, 4, 27)
R = (8, 3, 5, 2, 4, 7, 6, 9, 1)
(P, R) wurden auf der Grundlage der in GVS 300/82 dargelegten Theorie so
konstruiert, daß G(P, R) eine transitive Gruppe ist.
Der LZS besitzt die Eigenschaften:
- (P, R) sind regulär, (P,R) ∈ K1,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Dieser Langzeitschlüssel ist für die Erprobung von Programmen konstruiert.
// Für den Einsatz ist er verboten. Der LZS 25, 27 und 28 ist in Abt. XIII bekannt.
Der Langzeitschlüssel 29: (1982)
P = (28, 8, 33, 23, 11, 12, 5, 10, 9, 30, 19, 18, 4, 31,
21, 24, 13, 25, 22, 32, 20, 36, 27, 29, 7, 16, 15)
D = (0, 36, 28, 20, 24, 16, 4, 12, 8)
α = 2
Der LZS genügt der T 310-Algorithmus-Definition, GVS 190/79,
einschließlich dort angegebener Einschränkungen.
Der LZS besitzt die Eigenschaften:
- (P, D) sind regulär,
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial,
- der LZS ist kein (!) Element der Menge KT1 v KT2
- statistische Auswertungen verschiedener Zwischenfolgen des
T 310-Algorithmus mit dem LZS ergaben keine signifikanten
Abweichungen von der Irregularität bzw. waren die aufgetretenen
Abweichungen theoretische erklärbar.
// Für den Einsatz ist verboten!
Der Langzeitschlüssel 30: (1983)
P = (8, 28, 33, 3, 27, 20, 5, 16, 9, 1, 19, 23, 4, 2,
21, 36, 30, 25, 11, 24, 12, 18, 7, 29, 32, 6, 35)
D = (0, 36, 8, 28, 12, 32, 4, 20, 16)
α = 3
Der LZS besitzt die Eigenschaften:
- (P,D) ∈ KT1',
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
Die theoretischen und experimentellen Untersuchungen (z. B.
Äquivalenzen, statistische Eigenschaften, Wirksamkeit der
Schlüsselelemente, Perioden) unterstützen die Hypothese, daß
der T 310-Algorithmus mit diesem LZS gute kryptologische Eigen-
schaften besitzt.
// Für den Einsatz freigegeben.
Anhand des LZS des Deutschen Museum München konnte die
Platinennummer dem LZS zugeordnet werden.
// Auf KES 7905.15 und auf KES 7905.16 realisiert.
| Entsprechend der Realisierungshilfe |
|---|
| Karte 7905.15 |
| Fest verdrahtet | P | | | | | | | | | | | | | | | | | | | | | 25 | | | | | | | | 25 |
| U | | | | | | | | | | 12 | | | | | | | | 0 | 0 | | | | | | | | | | |
|
| von Karte .16 | P | 23 | 21 | 19 | | 13 | 10 | 4 | 1 | | | 23 | 21 | 19 | | 13 | 10 | 4 | | | 1 | | | | | | | | | |
| D/α | | 5 | | | 7 | | α | | | | | 5 | | | 7 | | α | | | | | | | | | | | | |
| U | | | | | | | | | 35 | | | | | | | | | | | | | 35 | | | 36 | | | 36 | |
|
| von | A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| nach | A | | 10 | | | | | | | | 2 | | | | | | | | | | | xx | | xx | xx | | xx | xx | | xx |
| B | 13 | | 10 | 23 | 25 | 22 | 24 | 14 | 3 | | 20 | 6 | 5 | 27 | 29 | 26 | 28 | 17 | 18 | | | 7 | | | 1 | | | 16 | |
| B | | | | | | | | 15 | | | | | | | | | | | | | | | | | | | | | |
|
| Fest verdrahtet | P | | | 27 | | | | 27 | 26 | 26 | | | | | | | | | | | | | | | | | | | | |
| D | 2 | 3 | | | | | | | | | | | | | 3 | 2 | 1 | 1 | | | | | | | | | | | |
| U | | | | 10 | 11 | 12 | | | | 11 | 10 | 6 | 7 | 8 | | | | | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
|
| von | B | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| B | | 21 | | xx | | | | 19 | 12 | | xx | 9 | | 15 | 14 | | | | 8 | | 2 | | | | | | | | |
| A | 25 | | 9 | | 13 | 12 | 22 | | | 3 | | | 1 | 8 | 8 | 28 | 18 | 19 | | 11 | | 6 | 4 | 7 | 5 | 16 | 14 | 17 | 15 |
|
| Karte 7905.16 |
| Fest verdrahtet | P | 16 | 17 | 20 | 11 | 10 | 8 | 6 | 4 | 2 | | 1 | | | | 21 | 22 | 23 | 25 | | | | | | | | | | | |
| D/α | | | | | | | | | | | | | | | | | | | α | | | | | | | | | | |
| U | | | | | | | | | | 36 | | | | | | | | | | 14 | | | | | | | | | |
|
| von | A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| nach | A | 10 | | | | 23 | | | 19 | | 1 | 21 | 1 | xx | xx | 27 | | 28 | | 8 | 25 | 11 | 8 | 5 | | 20 | | 15 | 17 | |
| A | 12 | | | | | | | 22 | | 12 | | 10 | | | | | | | 22 | | | 19 | | 1 | | | | | |
| B | | 4 | 21 | 24 | | 15 | 2 | | 14 | | | | | | | 23 | | 6 | | | | | | 3 | | 9 | 17 | | 10 |
| B | | | | | | 29 | 25 | | 18 | | | | | | | | | 16 | | | | | | | | | | | |
|
| Fest verdrahtet | P | | | 13 | | | | 12 | 5 | 19 | | | | | | | | | | | | | | | | | | | | |
| D | 7 | 8 | | | | | | | | | | | | | 9 | 6 | 5 | 4 | | | | | | | | | | | |
| U | | | | 30 | 31 | 32 | | | | 35 | 34 | 26 | 27 | 28 | | | | | 22 | 23 | 24 | 17 | 18 | 19 | 20 | 13 | 14 | 15 | 16 |
|
| von | B | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| B | 3 | 25 | 1 | | xx | 16 | 20 | 13 | | | xx | xx | 8 | 18 | 29 | 6 | | 14 | xx | 7 | | xx | | | 2 | xx | xx | xx | 15 |
| A | 24 | 7 | | 2 | | 18 | | | 26 | 29 | | | | 9 | 6 | | 27 | 9 | | | 3 | | 16 | 4 | 7 | | | | 6 |
| xx nicht angeschlossen - verdrahtet - verbunden |
Der Langzeitschlüssel 31: (1985)
Technische Umsetzung des Langzeitschlüssel 31
auf KES (Brückenplan)
Dieser Brückenplan wurde auf der Grundlage der
folgenden Dokumente erarbeitet:
- Übergabe eines operativen Langzeitschlüssels
für das Gerät T 310/51; GVS XI/378/86
- Operative T 310 - LZS: Schnittstelle mathema-
tische Darstellung - technische Realisierung
GVS XI/376/84
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16 A17 A18 A19 A20 A21 A22 A23 A24 A26 A27 A29 B1 B2 B3 B6 B7 B8 B9 B14 B15 B18
LZ der Karte 1 = 2: B14 A8 B1 B15 B22 B27 A2 B21 A20 B16 B2 B26 B17 B18 B11 B23 B9 B13 B8 B20 B4 B29 B19 A12 B12 B25
LZ der Karte 3: A22 B26 A28 B20 A26 B10 A10 B4 A24 B2 A13 B14 B18 B28 B19 A29 A21 B29 B17 B3 B6 B12 B23 B15 B16 B25 B21
P = (7, 4, 33, 30, 18, 36, 5, 35, 9, 16, 23, 26, 32, 12,
21, 1, 13, 25, 20, 8, 24, 15, 22, 29, 10, 28, 6)
D = (0, 16, 4, 24, 12, 28, 32, 36, 20)
α = 2
Der LZS besitzt die Eigenschaften:
- (P,D) ∈ L127 (Teilmenge von KT1')
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
Die theoretischen und experimentellen Untersuchungen (z. B.
Äquivalenzen, statistische Eigenschaften, Wirksamkeit der
Schlüsselelemente, Perioden) unterstützen die Hypothese, daß
der T 310-Algorithmus mit diesem LZS gute kryptologische Eigen-
schaften besitzt.
// Für den Einsatz freigegeben.
// Auf KES 7905.19 und auf KES 7905.20 realisiert.
Der Langzeitschlüssel 32: (1990)
P = (27, 30, 33, 24, 11, 36, 5, 20, 9, 23, 1, 34, 16, 14,
21, 8, 28, 25, 22, 32, 4, 10, 13, 29, 15, 12, 18)
D = (0, 20, 24, 4, 28, 8, 16, 36, 12)
T = (9,8,7,6,5,4,3,2,1)
α = 4
Der LZS besitzt die Eigenschaften:
- (P,D, α)wurde aus KT1 gewählt,)
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Für den Einsatz freigegeben.
Der Langzeitschlüssel 33: (1990)
P = (24, 3, 33, 30, 2, 8, 5, 12, 9, 1, 10, 6, 32, 22,
21, 18, 28, 25, 16, 20, 36, 13, 17, 29, 26, 4, 35)
D = (0, 12, 24, 36, 28, 16, 32, 8, 4)
T = (9,8,7,6,5,4,3,2,1)
α = 3
Der LZS besitzt die Eigenschaften:
- (P,D) ∈ L127 (Teilmenge von KT1')
- die Gruppe G enthält die alternierende Gruppe,
- die Automorphismengruppe Aut A ist trivial.
// Für den Einsatz freigegeben.
Zu Beachten ist bei Eigenentwicklung eines Langzeitschlüssels:
P3 = 33; P7 = 5; P9 = 9; P15 = 21; P18 = 25; P24 = 29;
Ansonsten erzeugt das unsymmetrisch arbeitende Schieberegister
sehr schnell voraussehbare bzw. zyklische Wurmreihen!
Ein dokumentierter Langzeitschlüssel dem noch keine Nummer zugeordnet werden kann:
Der Langzeitschlüssel ??: (1977)
P = (19, 1, 11, 10, 2, 13, 6, 7, 30, 3, 26, 31, 27, 25,
22, 15, 18, 33, 34, 14, 23, 5, 21, 17, 29, 9, 35)
R = (0, 3, 19, 23, 15, 27, 31, 7, 11)
// Dieser Langzeitschlüssel ist für die Erprobung von Programmen konstruiert.
// Für den Einsatz ist er verboten. Diese ist in Abt. XIII bekannt.
Für die Untersuchungen der Automorphismengruppe erstellt:
Der Langzeitschlüssel Untersuchung: (1985)
P = (18, 7, 8, 10, 11, 27, 13, 15, 14, 9, 16, 17, 24, 19,
20, 12, 22, 21, 23, 25, 1, 2, 3, 4, 5, 6, 26)
R = (7, 4, 3, 6, 9, 8, 5, 2, 1)
// Dieser Langzeitschlüssel ist für die Erprobung von Programmen konstruiert.
// Für den Einsatz ist er verboten. S. LSZ 25, 27 und 28.
Zeitschlüssel
Das Verfahren zum Einlesen des Zeitschlüssel (ZS) wurde vereinfacht
durch Lochkarten. Der ZS soll die Sicherheit der chiffrierten Infor-
mationen auch bei Kompromittierung des Chiffrierverfahrens gewährleisten.
Der ZS besteht aus 240 Bit. Die Anzahl der Bits auf der Schlüsselkarte
muß ungerade sein.
Nur die Entropie des Schlüssel beträgt 230 bit.
Das Schlüsselregister, der Schlüsselraum, ist 240 bit lang!
Schlüsselmittel Typ 796, Typ 758:
Der Typ 758 enthält neben den 14 Lochkarten ein Kenngruppenheft mit
14 Kenngruppen. Der Typ 758 ist für die zentrale Führungsebene aus-
gegeben worden. Der Typ 796 enthält 5 Kenngruppen und 5 Lochkarten.
Der Typ 796 sind für die Bezirks- und Kreiseinsatzleitungen bestimmt.
Siehe auch Schlüsselorganisation.
Der Zeitschlüssel wurde mit einem festen Algorithmus, kryptologisch definiert.
Aus dem Ergebnis meiner Untersuchung aller vorhandenen Zeitschlüssel,
ca. 20 Karten, kann zusammenfassend gesagt werden, das in jeder Zeile
die 1
7 bis 19 mal und im Abschnitt S1 bzw. S2 zwischen 45 und 71
mit einer 1
belegt sind.
Der Querschnitt für S1 ist 59,32 und für S2 ist 60,37.
Beispiele für den Typ 758 BArch*1
Abb. Schlüssellochkarte: Typ: 758 Serie: 002099 Exemplar: 001 Schlüssellochkarte Nr. 2 Sammler*56

Abb. Schlüssellochkarte: Typ: 758 Serie: 002100 Exemplar: 001 Schlüssellochkarte Nr. 1 Sammler*56

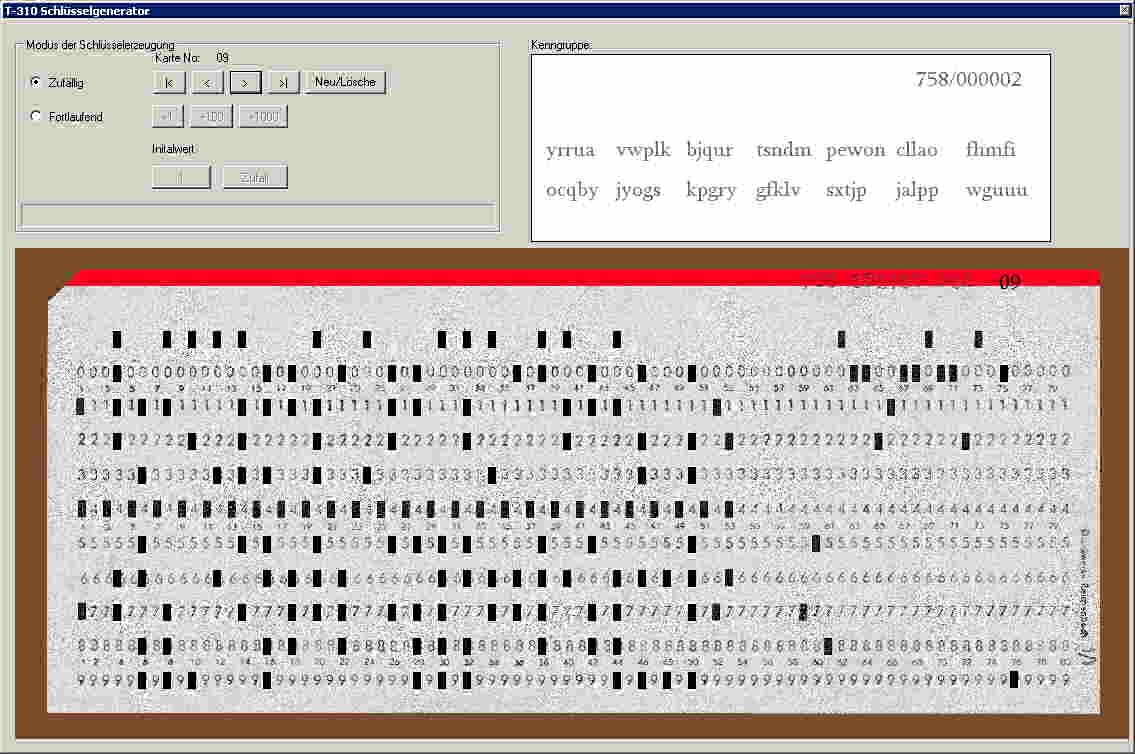
Abb.: Schlüsselgenerator - Software.
Wartungsschlüssel 1 bis 10:
Die Wartungsschlüssel dienen zur Überprüfung der im Chiffrator
implementierten Schlüsselprüfung. Wie z. B. die Einhaltung der ungeraden Parität des Schlüssels.

Abb. Wartungsschlüssel Nr. 1 (von 10)
Aufbau des Schlüssels:
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 10 | 11 | e |
| | | L | | | T | | | L | | | 1 |
| | | | | | | | | | | | 2 |
| | | | | | T | | | | | | 3 |
| 2/120 | 2/96 | 2/72 | 2/48 | 2/24 | | 1/120 | 1/96 | 1/72 | 1/48 | 1/24 | 4 |
| | | | | | T | | | | | | 5 |
| 2/119 | 2/95 | 2/71 | 2/47 | 2/23 | | 1/119 | 1/95 | 1/71 | 1/47 | 1/23 | 6 |
| | | | | | T | | | | | | 7 |
| 2/118 | 2/94 | 2/70 | 2/46 | 2/22 | | 1/118 | 1/94 | 1/70 | 1/46 | 1/22 | 8 |
| | | | | | T | | | | | | 9 |
| 2/117 | 2/93 | 2/69 | 2/45 | 2/21 | | 1/117 | 1/93 | 1/69 | 1/45 | 1/21 | 10 |
| | | | | | T | | | | | | 11 |
| 2/116 | 2/92 | 2/68 | 2/44 | 2/20 | | 1/116 | 1/92 | 1/68 | 1/44 | 1/20 | 12 |
| | | | | | T | | | | | | 13 |
| 2/115 | 2/91 | 2/67 | 2/43 | 2/19 | | 1/115 | 1/91 | 1/67 | 1/43 | 1/19 | 14 |
| | | | | | T | | | | | | 15 |
| 2/114 | 2/90 | 2/66 | 2/42 | 2/18 | | 1/114 | 1/90 | 1/66 | 1/42 | 1/18 | 16 |
| | | | | | T | | | | | | 17 |
| 2/113 | 2/89 | 2/65 | 2/41 | 2/17 | | 1/113 | 1/89 | 1/65 | 1/41 | 1/17 | 18 |
| | | | | | T | | | | | | 19 |
| 2/112 | 2/88 | 2/64 | 2/40 | 2/16 | | 1/112 | 1/88 | 1/64 | 1/40 | 1/16 | 20 |
| | | | | | T | | | | | | 21 |
| 2/111 | 2/87 | 2/63 | 2/39 | 2/15 | | 1/111 | 1/87 | 1/63 | 1/39 | 1/15 | 22 |
| | | | | | T | | | | | | 23 |
| 2/110 | 2/86 | 2/62 | 2/38 | 2/14 | | 1/110 | 1/86 | 1/62 | 1/38 | 1/14 | 24 |
| | | | | | T | | | | | | 25 |
| 2/109 | 2/85 | 2/61 | 2/37 | 2/13 | | 1/109 | 1/85 | 1/61; | 1/37 | 1/13 | 26 |
| | | | | | T | | | | | | 27 |
| 2/108 | 2/84 | 2/60 | 2/36 | 2/12 | | 1/108 | 1/84 | 1/60 | 1/36 | 1/12 | 28 |
| | | | | | T | | | | | | 29 |
| 2/107 | 2/83 | 2/59 | 2/35 | 2/11 | | 1/107 | 1/83 | 1/59 | 1/35 | 1/11 | 30 |
| | | | | | T | | | | | | 31 |
| 2/106 | 2/82 | 2/58 | 2/34 | 2/10 | | 1/106 | 1/82 | 1/58 | 1/34 | 1/10 | 32 |
| | | | | | T | | | | | | 33 |
| 2/105 | 2/81 | 2/57 | 2/33 | 2/9 | | 1/105 | 1/81 | 1/57 | 1/33 | 1/9 | 34 |
| | | | | | T | | | | | | 35 |
| 2/104 | 2/80 | 2/56 | 2/32 | 2/8 | | 1/104 | 1/80 | 1/56 | 1/32 | 1/8 | 36 |
| | | | | | T | | | | | | 37 |
| 2/103 | 2/79 | 2/55 | 2/31 | 2/7 | | 1/103 | 1/79 | 1/55 | 1/31 | 1/7 | 38 |
| | | | | | T | | | | | | 39 |
| 2/102 | 2/78 | 2/54 | 2/30 | 2/6 | | 1/102 | 1/78 | 1/54 | 1/30 | 1/6 | 40 |
| | | | | | T | | | | | | 41 |
| 2/101 | 2/77 | 2/53 | 2/29 | 2/5 | | 1/101 | 1/77 | 1/53 | 1/29 | 1/5 | 42 |
| | | | | | T | | | | | | 43 |
| 2/100 | 2/76 | 2/52 | 2/28 | 2/4 | | 1/100 | 1/76 | 1/52 | 1/28 | 1/4 | 44 |
| | | | | | T | | | | | | 45 |
| 2/99 | 2/75 | 2/51 | 2/27 | 2/3 | | 1/99 | 1/75 | 1/51 | 1/27 | 1/3 | 46 |
| | | | | | T | | | | | | 47 |
| 2/98 | 2/74 | 2/50 | 2/26 | 2/2 | | 1/98 | 1/74 | 1/50 | 1/26 | 1/2 | 48 |
| | | | | | T | | | | | | 49 |
| 2/97 | 2/73 | 2/49 | 2/25 | 2/1 | | 1/97 | 1/73 | 1/49 | 1/25 | 1/1 | 50 |
| | | | | | T | | | | | | 51 |
| | | L | | | | | | L | | | 52 |
| | | | L | | T | | L | | | | 53 |
Anmerkung:
-e- Zählindex der Spalten der Schlüssellochkarte
-L- Organisationslochungen
-T- Lesetakt
-1/1 bis 1/120- Elemente der Schlüsselfolge S1
-2/1 bis 2/120- Elemente der Schlüsselfolge S2
Die Spalte 54 bis 80 werden genutzt für die Beschriftung der Lochkarte (s.o.)
Diese sind nicht relevant für das Gerät und werden auch nicht gelesen.

Abb.: Ansicht der baugleichen Schlüsselregister SR1 bzw. SR2
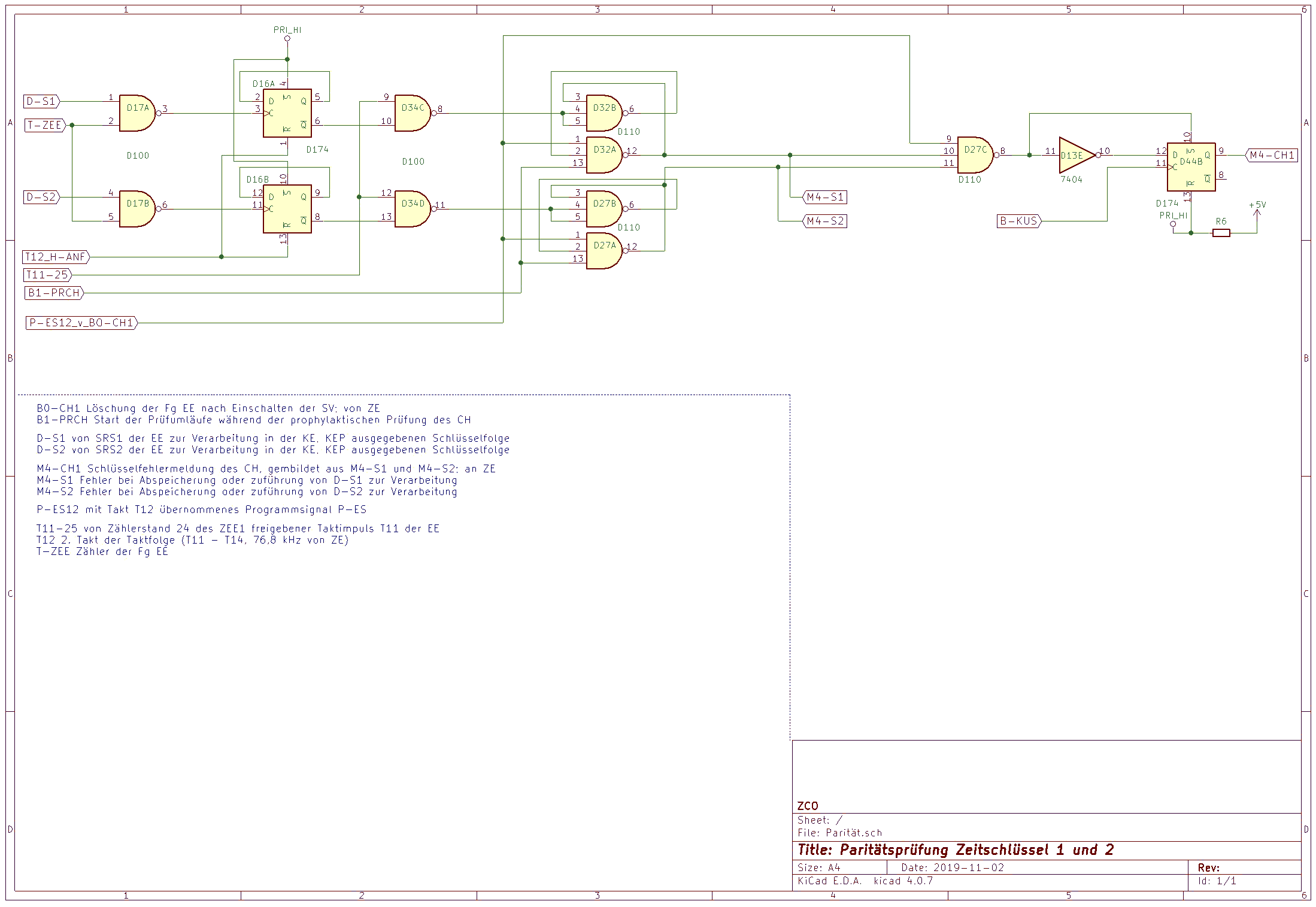
Abb.: Schaltung der Paritätsprüfung des Zeitschlüssels
Der Langzeitschlüssel wurde auf 3 Steckkarten realisiert, die sich auf 3 identischen
Leiterplatten der Komplizierungseinheit befinden.
Der Brückenplan und seine mathematische Beschreibung ist oben beschrieben.

Abb.: Langzeitschlüssel mittels Steckkarten auf der Leiterkarte der Komplizierungseinheit.

Abb.: Speicherkarte S1 des Zeitschlüssels

Abb.: Speicherkarte S2 des Zeitschlüssels