Die Anwendung der Enigma auf dem Gebiet der DDR von 1949 bis 1990 ist
dokumentiert in:
BArch*201, *310, *691, NSA*1
Einleitung zum Thema "Die ENIGMA in der DDR"
Aus den Unterlagen des Bundesarchiv läßt sich grob der Einsatz
der ENIGMA in der DDR ermitteln.
In dem Nachrichtenausbildungszentrum 12 (NAZ-12) bzw. Mili-
tärtechnische Schule MtS(N) in Frankfurt/Oder befand sich bis
1989 in dem Ausstellungsraum historischer Chiffriergeräte die
seit 1949 eingesetzten Chiffrier- und SAS-Geräte. Über den
Verbleib nach 1990 kann nur die Bundeswehr Auskunft gegeben.
Hier befand sich auch eine funktionierende ENIGMA.
Aus den "Erinnerungen" des Fregattenkapitän Riebe ist er-
sichtlich, daß in der Volksmarine 100 ENIGMA eingesetzt waren
und diese neu verdrahtet wurden. Diese kamen aber nur in
stationären Einrichtungen und nicht auf Booten oder Schiffen
zum Einsatz.
Eine Bestätigung ist in den Unterlagen des Bundesarchiv, die
vom BND stammen, zu finden. Dort wird über die Schulung der
Kasernierten Volkspolizei (KVP später NVA) an der ENIGMA
bereits 1952 berichtet.
Im Jahr 1954 stellte Leutnant Weder einen Änderungsvorschlag
zur Nutzung der ENIGMA. Dieser wurde nicht zugelassen, da es
zu umständlich war und das Chiffrierverfahren nicht verbes-
serte.
Aus den Archivunterlagen der NSA ist dokumentiert das bis ins
Jahr 1956 die mit der ENIGMA chiffrierten Funksprüche dekryp-
tiert wurden. Es handelte sich um Funksprüche der Volkspolizei
und der Feuerwehr.
Die aktive Kontrolle des chiffrierten Funkverkehrs mit der
Darstellung eines dekryptierten Funkspruches im Jahr 1961
zeigt, das das ZCO fähig war ENIGMA-Funksprüche zu dekryptieren.
Das Betrifft auch Sprüche aus Länder in denen nach 1945 die
ENIGMA als "Geschenk" für die "Dritte Weltländer" und Israel
übergeben wurden.
Erste Dokumente aus dem Bundesarchiv belegen die mathematisch-
wissenschaftliche Auseinandersetzung mit der ENIGMA.
Auch wird die rechentechnische Bearbeitung von ENIGMA Sprüchen
erwähnt.
Diese endete 1968 mit der Abschlußarbeit der Mathematischen
Darstellung der Chiffrierung und deren Archivierung im ZCO.
Aufgrund der dokumentierten Daten wurde an der ENIGMA I mit
den Walzen I bis VI gearbeitet bzw. waren im Einsatz.
Zum Einsatz kamen Methoden die auch von den polnischen Krypto-
logen Rejewski, Rozycki und Zygalski genutzt wurden.
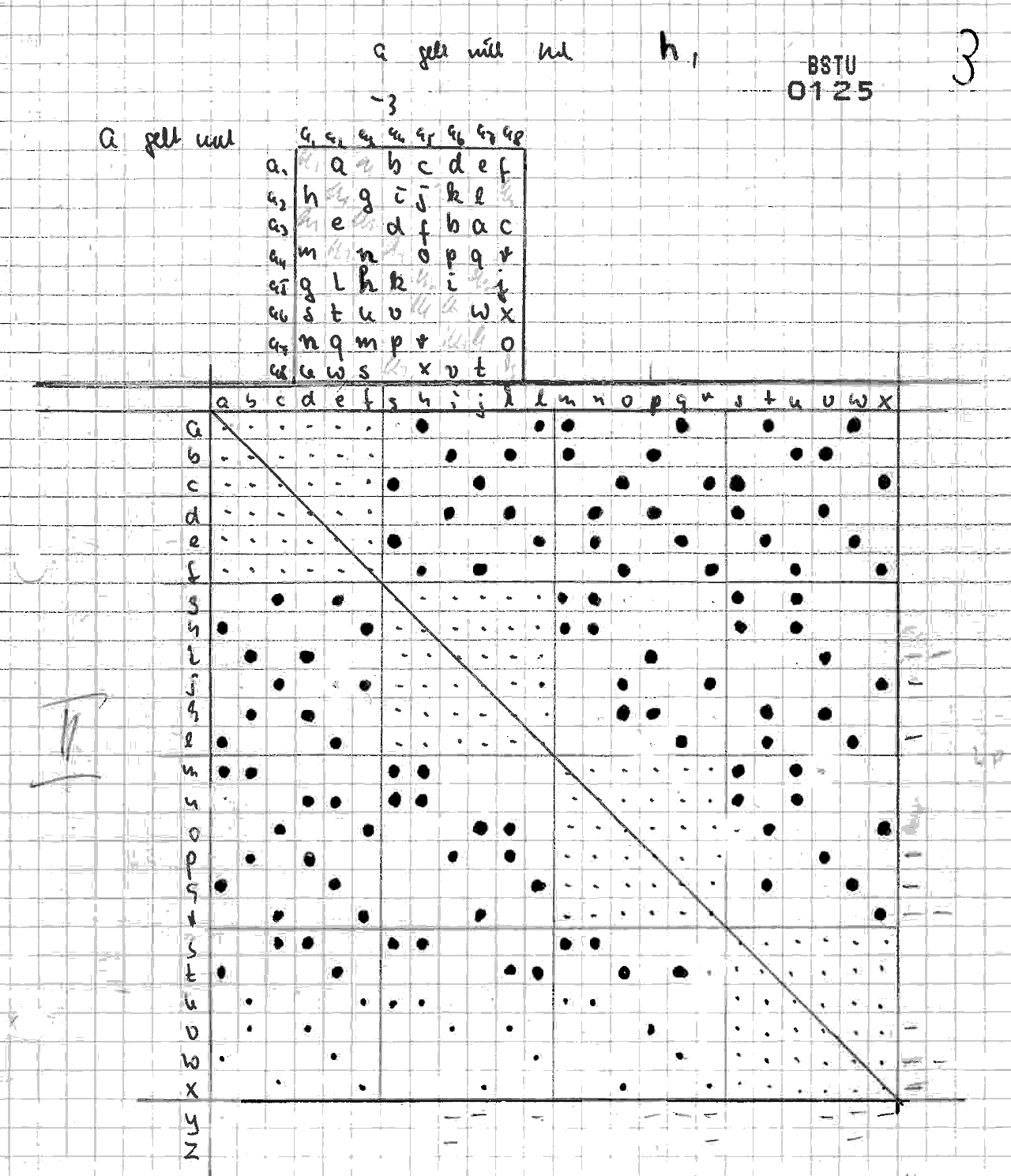
Abb.: Matrizze
Freie Übersetzung des NSA Artikels über die Enigma in der DDR. NSA
Englischer Text.
DOCID: 3101787
William T. Kvetas, Center for Cryptologic History, 972-2893s
Cryptologic-Almanach 50. Jahrestag
Die letzten Tage der Enigma.
Nach dem Hören der vielen interessanten Geschichten über
die Entschlüsselung der Enigmasprüche (der 2. Weltkrieg wurde
mindestens um ein Jahr verkürzt, Erfolge in der Nordatlantik
und bei der Unterstützung im Kampf in Europa), habe Sie sich
schon gefragt wie die Geschichte um die Enigma endet?
Die Geschichte der Enigma begann in den späten 20. und Anfang
der 30. des 20 Jahrhunderts. In diesem Zeitraum wurde die
Enigma Kommerziell genutzt. Die Polen sahen die Bedrohung
durch die Politik Deutschlands und die von der Enigma, die
zu militärischen Zwecken genutzt werden kann. Sie erwarben
und erbeuteten die Enigma. Sie erarbeiteten Wege zur
Dekryptierung. Im Jahr des Überfalls Deutschland auf Polen,
1939, gaben die Polen ihr Wissen an Frankreich und
Großbritannien weiter. Die Briten machten große Erfolge mit
der Brechung der Enigmasprüche und entwickelten die Bombe
weiter. Die Bombe
war ein großes elektromechanisches
Gerät das nach Analyse der Texte die Gültigkeit der
vorgeschlagenen Lösungen prüfte. Die Polen bauten das erste
Gerät das die Briten weiterentwickelten. Die USA verfeinerten
anhand der vorhanden Bombe
das Verfahren. Viele Nachrichten
sind über den weg entschlüsselt worden. Es wurde Maßnahmen
zum Schutz der Information, das die Enigma gebrochen wurde,
ergriffen. Kinofilme und Dokumentationen stellten die gewaltigen
Anstrengungen dar um die Sprüche der Enigma zu knacken und die
Schlüssel zu ermitteln. Maßnahmen zur Ermittlung der Schlüssel
und der modifizierten Enigma waren die Erbeutung von Schiffen
und U-Boote der deutschen Marine.
Das Ende des 2. Weltkrieges war aber nicht das Ende der Enigma.
Sein unsichtbarer Tod in Europa erfolgte im Jahre 1955. Die DDR
verwendeten weiterhin die Enigma, deren Einsatz sich aber
verminderte. Ab 1950 wurde die Enigma nur noch in Berlin genutzt.
Zur Identifikation der Kommunikation wurde ein vorgeschriebenes
System verwendet. Zum Beispiel: GCPB 00101, GC steht für die DDR,
P steht für Polizei, B steht für Handbuch Morse
, 001 ist die
Anzahl der Nachrichtennetze, und 01 der Teilnehmer im Netzwerk.
In diesem Fall ist es das Nachrichtennetz 001, es gab nur das
eine in Ostberlin. Und 01 war die Polizeizentrale in Berlin.
Der Inhalt der Meldungen des letzten Enigmanetzes waren Feuer-
schadensmeldungen, vorbereitende Maßnahmen verschiedener Feuer-
wehren, Polizeiberichte, unbedeutende Festnahmen. Die Meldungen
sind nicht spannend wie die Meldungen im 2. Weltkrieg aber zum
überwachen der DDR war ihre Priorität sehr hoch angesetzt.
Analytiker verstanden nicht warum diese Informationen eine hohe
Priorität erhielten. Der Berliner Tunnel
, in denen die USA
viele Informationen erhielten, war mit den Enigmasprüchen ein
von vielen Puzzle-Steinen die ein Bild von der DDR und der Sowjet-
union lieferten. Inwiefern Georg Blake, vom MI-6, Einfluß auf
die Informationen hat die im Berliner Tunnel
abgefangen wurde
ist nicht bekannt.
Im Jahr 1956 hat Ellie Carmen Klitzke in der Arlington Hall Station,
Leiter der kryptoanalytischen Abteilung für den Bereich der DDR,
Prestion Welch benachrichtigt das die Arbeit auf dem Gebiet der
Enigma beendet werden. Elliot Welch war Kryptoanalytiker und
entwickelte die Menüs
mit dessen Hilfe die Bombe
entsprechend
zur Entschlüsselung der Sprüche eingestellt wurden. Die Menüs
wurde anhand von Schlüsselwörtern erstellt. Pfingstmontag hatte
Preston Welch das letzte Paket für die Menüs
erhalten.
Im National Cryptologic Museum ist eine Bombe
zu sehen.
William T. Kvetas, Zentrum für Cryptologic Geschichte, 972-2893s
Aus dem Original übernommen:
DOCID: 3101787
William T. Kvetas, Center for Cryptologic History, 972-2893s
Cryptologic Almanac 50th Anniversary Series
The Last Days of Enigma
After hearing the many intriguing success stories about the exploitation
of Enigma communications (shortening WII by at least a year, successes
in the battle of North Atlantic, support to battle in Europe), did you
ever wonder how it all ended?
Use of Enigma started modestly in the late 1920s and early 1930s with
the machine being applied to commercial uses. Only the Poles, however,
who were more keenly aware than most of the German threat, saw the
potential dangers of Engima being used for military purposes. They
acquired a machine and started working on ways to exploit the problem.
In 1939 with the German invasion of Poland, the Poles passed their
knowledge to the British and French. The British made great progress
advancing the art of break Enigma, and continued developing the bombe
used in breaking the Enigma message. The bombe was huge electromechanical
device, which could analyz cassumed text and determine the validity of
the proposed solution. The Poles conceived and built the device, and the
British developed its application. The British in turn involved the U.S.,
which refined the bombes′s use in decrypting the Eingma messages.
Volumes have been written about the value of the Enigma decrypts during
WII and the extreme measures taken to protect the successes. Movies havebeen
made depicting the extraordinaty efforts taken to acquire new Enigmamachines
and the keys used. The most popular undertakings were the effortsto capture
German submarintes in order to get the cryptographic materials.
At the end of WW II, contrary to what one might believe, the use of Enigma
did not case in a bunker in Berlin in 1945. It lingered on to an insignificant
demise in 1955. The East Germans continued to use the Enigmaequipment, but its
role diminished, until by the early 1950s they were usingit only in Berlin.
Case notations were used to identify discrete communication sentities so that
one could follow and maintain continuity on a given set of communications.
These designators were assigned according to a prescribed system. For instance,
in GCPB 00101, the GC
denoted East German, The P
indicated Police, and the
B
meant that the mode of communications was Manual Morse. The 001
and 01
signify the number of the network and the net within the network. In this case
we have only one net and that was the East German police in Berlin. GCPB 00101
was the last communications network to carry Enigma trafic, which the U.S.
exploited.
The content of the communications carried on GCPB 00101 could be described as
mundane at best. It contained fire demage reports, state of readiness of varous
fire stations and police reports, mostly regarding insignificant arrests.
This was not ehe exciting content produced during WWII,yet the priority to
intercepting this trafic was extremly high. People working in the traffic
analytic aspects of the problems and those continuing the efforts to read the
message could not understand why the mundane content of the messages would
warrant the high priority afforded this target in the mid-1950s. Obviously
those in the hierarchy at that time knew, but the rest could only speculate.
In retrospect it would appear that, with the famous Berlin Tunnel
operation
under way, the U.S. was most intersted in knowing about any reflection or
knowledge on the part of East German of the tunnel′s construction and activites.
Police and fire reports might just provide such information and hence the high
priority given to GCPB 00101. Litlle did we know at that time that the noted
British traitor, Gerorg Blake from MI-6, in all probability had already had
compromised the tunnel operation.
Then one day in 1956 Ellie Carmen Klitzke, chief of East German cryptanalytic
section located in A Building at Arlingten Hall Station, notified
Preston Welch that the effort on Enigma was to be terminated. Preston was the
cryptanalyst in charge of developing menus
to be run on the bombe. These
menus were short passages of text, which he suspected were in the encrypted
message. The menus were run on the bomb and, if the guess were correct, the
bomb would yield the setting for that message so that it and other messages
could be read.
Whit a modest degree of fan fare, Preston held up a package and announced that
it contained the last menus to be run on the bombe. He handed the package to a
cryptanalytic intern who caught the shuttle bus from Arlington Hall Station to
the Naval Security Station and delivered the menus to the Navy Waves who ran
the bombe. They in turn ran the machine for the last time. By way of footnote,
one of the last bombes used is on display at the National Cryptologic Museum.
Wissensspeicher des ZCO Akte ENIGMA; 1950 … 1961
VVS 1069/59/721 1959
1. Ausfertigung 8 Blatt
Az.: G604
Zur Enigma:
1) Aufstellung der Strukturformel:
a) Schlüsselelemente sind: 3 bewegliche Walzen X, Y, Z;
Umkehrwalze U; Steckerverbindung K.
b) Schrittschaltwerk: Jede Tastung bewegt die erste Walze X
um einen Schritt vorwärts. Die 26. Tastung bewirkt die
Fortschaltung der zweiten Walze Y um einen Schritt, wonach
diese wieder solange in Ruhe bleibt, bis die Walze X
wiederum den 26. Schritt vollführt. Die Walze Z wird erst
dann um einen Schritt fortbewegt, nachdem die zweite Walze
Y den 26. Schritt vollführt hat etc. -> Korrektur in Stellungnahme
Der tatsächliche Fortschaltrhytmus wird - obwohl periodisch -
druch die an den Walzen angebrachten Schrittschaltkerben
geregelt.
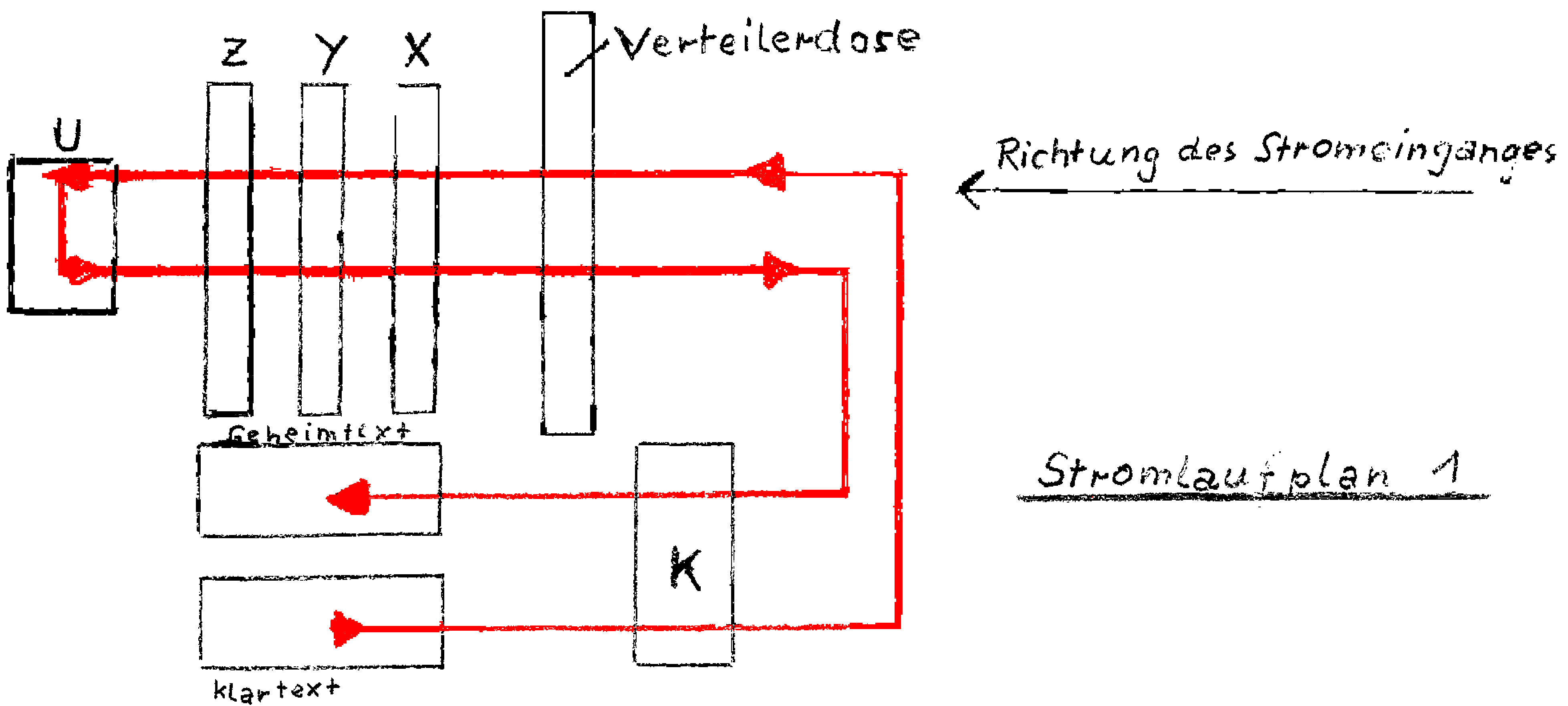
c) Die Bewegungsrichtung des Schrittschaltwerkes ist:
in Richtung des Stromeingangs gegen den Uhrzeigersinn zu
rechnen.
Die Permutationen in den Walzen X, Y, Z sind in Richtung
des Stromeingangs betrachtet im Uhrzeigersinn angeordnet,
d. h. die alphabetische Anordnung der oberen Zeile der
Permutationen

verläuft auf der Seite der Kontaktplättchen im Uhrzeiger-
sinn, hingegen auf der Seite der Kontaktstifte gegen den
Uhrzeigersinn.
d) Jedes Schlüsselelement wird, wenn der Stromlaufplan vom Klar-
textteil aus verfolgt wird, mit Ausnahme von U zweimal
durchlaufen, wobei durch U die Umkehr erfolgt. Die Schlüs-
selelemente X, Y, Z und K werden somit nach U invers durch-
laufen.
Auf Grund dessen kann der Stromlaufplan 1 auch durch folgende
Skizze ersetzt werden:
Stromlaufplan 2

Zwischen K - X, X - Y, y - Z und Z - U ergeben sich durch
die Schleifkontakte bestimmte Übergangspermutationen Ti, die
sich auf Grund der Beweglichkeit von X, Y, Z nach jedem
Schritt ändern. Da die Fortschaltung in Einzelschritten
erfolgt, haben alle Übergangspermutationen den Charakter
zyklischer Permutationen.
Sämtliche Ti werden durch Potenzen der erzeugenden Rela-
tionen
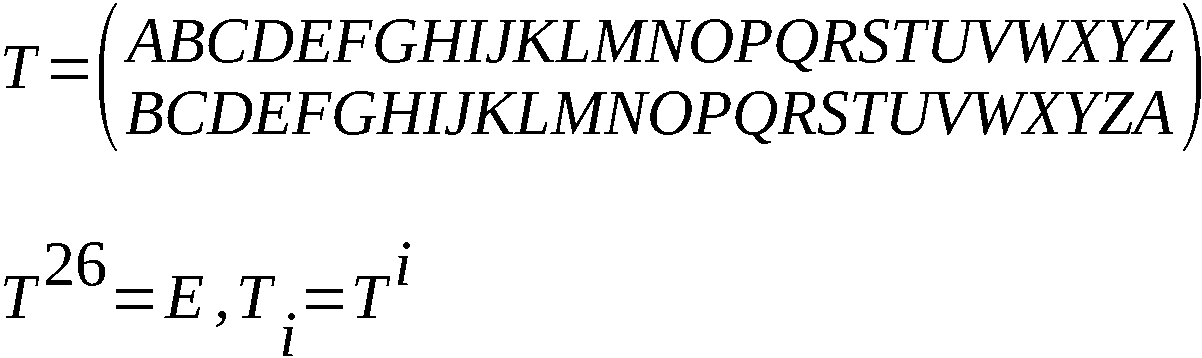
dargestellt. i = Anzahl der Schritte
Die Ti, i = 0, 1, 2, 3, …, 25 bilden eine reguläre Permu-
tationsgruppe Ƭ, deren Ordnung und Grad gleich 26 ist.
Überdies haben die Permutationen U und K die Ordnung 2.
Sie zerfallen in 13 elementfremden Zweierzyklen. Es gibt
U2 = E. K2 = E.
Die Gruppen
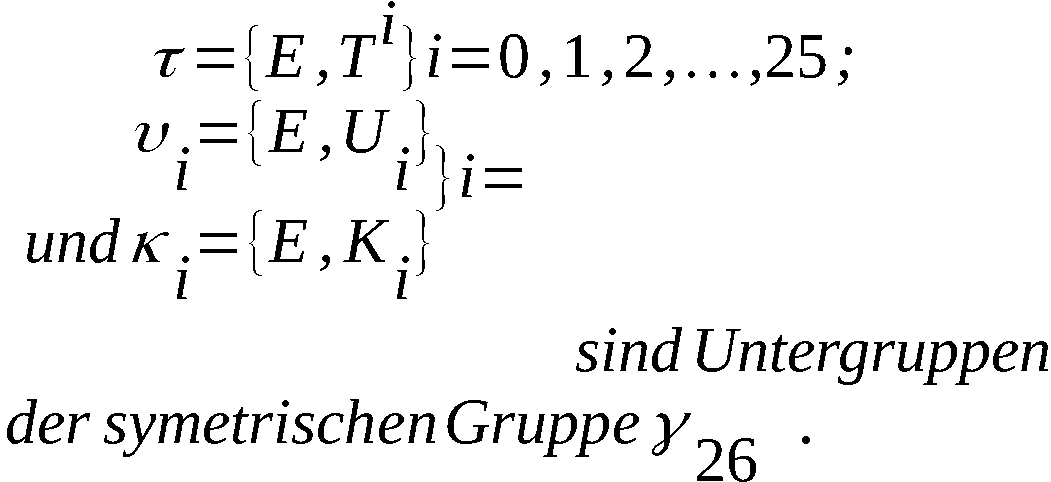
Seien K > l > m bezüglich einer Ausgangslage (einheitliche
Lage der Transportkerben) die Anzahl der Schritte, welche
die Walzen X, Y, Z erlitten haben, dann hat die Walze X
gegenüber der festbleibenden Verteilerdose K Schritte Fort-
schaltung erfahren.
Die Walze Y ist aber (da diese nur um l schritte fortbewegt
wurde) gegenüber der Walze X um K - l Schritte im Rückstand.
Schließlich hat sich die Walze Z gegenüber der festbleibenden
Umkehrwalze U um m Schritte fortbewegt.
Dies läßt sich an folgender Skizze klarmachen:

Die Exponenten der Übergangspermutationen werden in Richtung
gegen den Uhrzeigersinn positiv und in Richtung mit dem Uhr-
zeigersinn negativ gerechnet, so daß also die Exponenten
der Übergangspermutation für die Walzen eingangsseitig
positiv und ausgangsseitig negativ gerechnet werden.
Es ist also auf die Ausgangslage der Verteilerdose bezogen
die Übergangspermutation von Verteilerdose auf Walze X → Tk,
Walze X Walze Y → T-k
Verteilerdose Walze Y → Tl
Walze Y Walze Z → T-l
Verteilerdose Walze Z → Tm
Walze Y Walze U → T-m
Wobei die Y, Z die Walzen in der Ausgangsstellung
bezeichnen sollen.
Die direkten Übergangspermutationen sind somit gegeben
durch:
Übergangspermutation von Verteilerdose auf Walze X → Tk
Walze X Walze Y → T-k+l
Walze Y Walze Z → T-l+m
Walze Z Walze U → T-m
Diese Übergangspermutationen werden auf dem Rückweg (also
nach U) invers durchlaufen.
Man bekommt bei jeder Tastung für das Klaralphabet eine
Substitution S (Geheimalphabet), die durch folgende Ver-
knüpfung (nach Stromlaufplan 2) gegeben ist:
S = K·Tk·X·T-k+l·Y·T-l+m·Z·T-m·U·TmZ-1·T-m+l·Y-1·T-l+k·X-1·T-k·K-1
oder umgeformt:
S = K·(Tk·X·T-k)·(Tl·Y·T-l)·(Tm·Z·T-m)·U·(Tm·Z-1·T-m)·(Tl·Y-1·T-l)·(Tk·X-1·T-k)·K-1
mit S2 = E
für X = Y = Z = E wird S zu
S = K·U·K-1 = K·U·K, weil K-1 = K
Da während der Chiffrierung K, U = constant sind, so folgt
daraus S = constant; d. h. es ergibt sich ein monoalphabe-
tisch einfaches Chiffrierverfahren für diese spezielle Vor-
aussetzungen.
Für X = Y = Z = E und K = U ergibt sich wegen
K2 = E und U2 = E
für S die Beziehung
S = U,
ebenfalls ein monoalphabetisch einfaches Chiffrierverfahren.
Die konstante Substitution S entspricht in beiden speziellen
Fällen einem Chiffrieralphabet, in dem zwischen Klar- und
Chiffrierkomponente eine reziproke Zuordnung besteht.
Für die Exponenten k, l, m gilt überdies
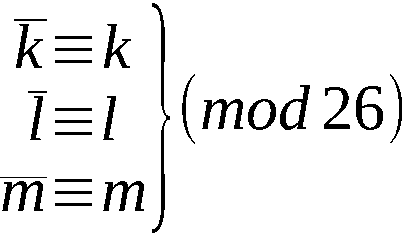
Das folgt aus den Eigenschaften der Permutation Ti; denn
es ist T26 = E.
2) Rekonstruktion der Permutation der Walze X:
Seinen X, Y, Z die den Walzen zugrundeliegenden Permutationen
und U die Permutation der Umkehrwalze, die als unbekannt vor-
rausgesetzt werden, Die Maschine arbeitet ohne die Steckerver-
bindung K.
Gegeben sei lediglich die durch irgendeine Einstellung bewirkte
Ausgangssubstitution S0 und die durch Fortschaltung der
Walze X (um einen Schritt) bewirkte nachfolgende Substitution S1.
Also
( 1 ) S0 = X·Y·Z·U·Z-1·Y-1·X-1
S1 = T·X·T-1·Y·U·Z-1·Y-1·T·X-1·T-1
Für die Ausgangslage kann willkürlich k = l = m = 0 gesetzt
werden. T ist von vornherein bekannt. Aus den beiden gegebenen
Substitutionen läßt sich die Walzenpermutation ermitteln, aller-
dings nur relativ in ihrer Lage zum Ziffernring der Walze.
Aus beiden Gleichungen von ( 1 ) wird U eliminiert. Man
erhält zunächst U = Z-1·Y-1·X-1·S0·X·Y·Z.
Das eingesetzt in die zweite Gleichung ergibt
S1 = T·X·T-1·X-1·S0·X·T·X-1·T-1
oder umgeformt
(X·T·X-1)·(T-1·S1·T) = S0·(X·T·X-1)
oder P·R = S0·P
mit P = X·T·X-1 und R = T-1·S1·T ( 2 )
Überdies ist unter anderem P2 = X·T2·X-1 und
allgemein Pi = X·Ti·X-1 I = 1, 2, …, 25, P0 = E
Aus P = X·T·X-1 folgt, da P und T konjugierte Elemente sind, daß
P die gleichen Eigenarten aufweist wie T, also alle zu einer
Gruppe Ƥ gehörenden Elemente P zyklisch sind (aus nur einem Zyklus der
Länge 26 bestehend), daß Grad und Ordnung übereinstimmen und
demzufolge alle Elemente Ƥ durch Potenzen des erzeugenden
Elementes P darstellbar sind. Insgesamt besteht Ƥ aus 26 Elementen.
Dieselbe Überlegung kann für R = P-1·S0·P angestellt werden.
R und S0 sind zueinander konjugierte Elemente.
Demzufolge kann P aus S0 und R durch Erprobung nach endlich
vielen Schritten rekonstruiert und gefunden werden. S0 und
R = T-1·S1·T sind oben die als bekannt vorausgesetzten
Substitutionen.
P wird gefunden, indem S0 als obere Zeile und R als untere
Zeile der Permutation P eingesetzt wird. Symbolisch dargestellt
etwas durch

wobei für S0 und R die Zyklendarstellung einzusetzen ist.
S0 und R zerfallen auf Grund ihrer Eigenschaften stets in 13
zueinander elementfremde Zweierzyklen. Von P ist nur bekannt,
daß es aus einem einzigen Zyklus der Länge 26 besteht.
Durch Permutation der Zweierzyklen von R und ihrer Zuordnung
zu den als feststehend zu betrachtenden Zweierzyklen von S0 und
durch zyklische Vertauschung der Elemente in den Zyklen von R,
kann P gefunden werden.
Die gefundene Permutation muß sich als ein Zyklus der Länge
26 darstellen lassen. Unter allen diesen Permutationen befindet
sich P.
Beispiel:
Es seien zum Zwecke der Überprüfung auch die als unbekannt
anzusehenden Permutationen angegeben.

Bekannt sind:
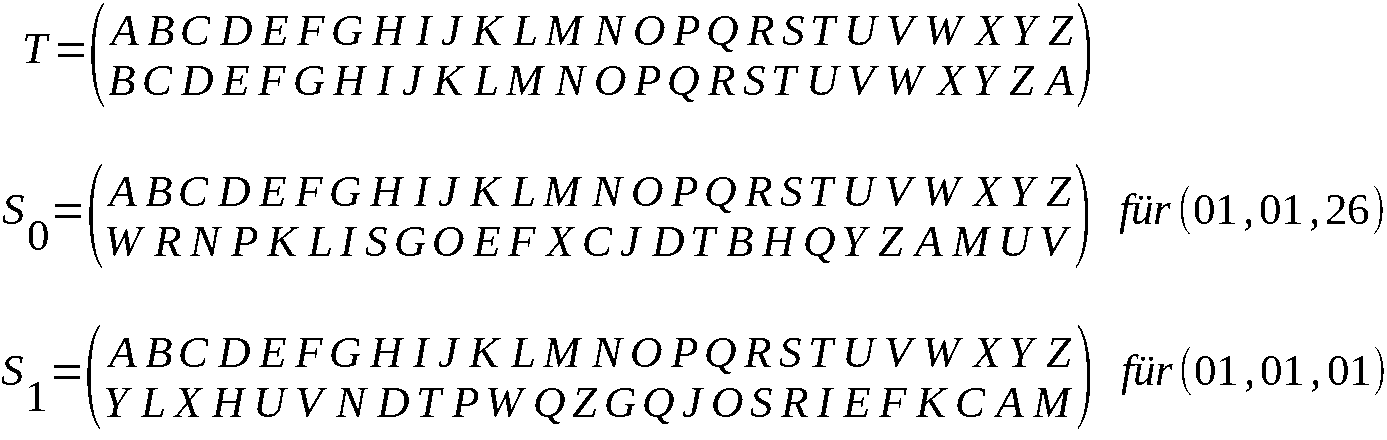
und damit auch

Als unbekannt sei noch angeführt

Es galt also

Die Zyklendarstellung von S0 und R sind
S0 = (AW)(BR)(CN)(DP)(EK)(FL)(GI)(HS)(JO)(MX)(QT)(UY)(VZ)
R = (AN)(BZ)(CM)(DY)(EI)(FV)(GW)(HO)(JU)(KQ)(LX)(PR)(ST)
somit ist zunächst

welches mit dem oben als noch unbekannt aufgeführten P überein-
stimmt, denn auf die Reihenfolge der Zuordnungspaare kommt es
in einer Permutation nicht an.
Überdies ist dieses P tatsächlich durch einen einzigen Zyklus
der Länge 26 darstellbar.
Insgesamt lassen sich auf diese Weise, um P zu finden
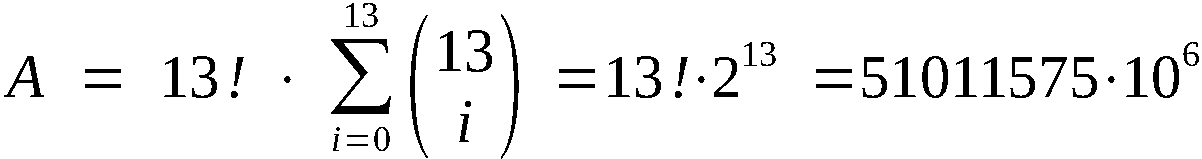
Permutationen bilden, unter denen die wenigsten einen ein-
gliedrigen Zyklus darstellen.
Allgemein gilt für diese Permutationsgewinnung, wenn die Aus-
gangspermutationen (sinngemäß dann S0, R) in ein Produkt von
Zyklen verschiedener Länge zerfallen, die Cauchysche Formel

Ist nun auf diese Art P gefunden worden, so läßt sich ver-
hältnismäßig leicht X finden. Das Verfahren ist dasselbe, wie
das, um P zu finden. Die Anzahl A der möglichen permutativen
Darstellungen, aus denen X zu finden ist, ist aber wesentlich
geringer.
Es ist A = 261·1! = 26, weil nur 1 Zyklus der Länge 26.
Ausgegangen wird von der Beziehung
P = X·T·X-1 oder X-1·P = T·X-1
man hat dann wiederum
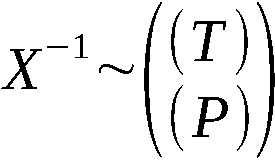
anzusetzen.
Fortführung des Beispiels:

was mit dem im Beispiel bereits angegebenen, aber als unbe-
kanntes X vorausgesetzt, übereinstimmt.
Information aus dem Arbeitgebiet Dekryptierung
Am 25.9.1961 fielen folgende Texte an:
1. AN ANKER VON PUDEL
MASCHINENSCHLUESSEL VON HEUTE UEBERPRUEFEN:
2. AN ALLE VON ANKER
DIE WALZEN NR PKT DES MASCHINENSCHLUESSELS FUER DEN
25.9.61 IST IN WALZEN NR PKT IV UMZUAENDERN.
NICHT WIE ANGEGEBEN VI.
Die folgenden Daten der ENIGMA entsprechen denen der ENIGMA I
mit der Umkehrwalze UKW-B.
Wobei Walze X, Y, Z == I, II sowie III sind.
Verdrahtung der Umkehrwalze:
(AY)(BR)(CU)(DH)(EQ)(FS)(GL)(IP)(JX)(KN)(MO)(TZ)(VW)
Verdrahtung der Walze X:
(AE)(BK)(CM)(DF)(EL)(FG)(GD)(HQ)(IV)(JZ)(KN)(LT)(MO)(NW)(OY)(PH)(QX)(RU)(SS)(TP)(UA)(VI)(WB)(XR)(YC)(ZJ)
Verdrahtung der Walze Y:
(AA)(BJ)(CD)(DK)(ES)(FI)(GR)(HU)(IX)(JB)(KL)(LH)(MW)(NT)(OM)(PC)(QQ)(RG)(SZ)(TN)(UP)(VY)(WE)(XV)(YO)(ZE)
Verdrahtung der Walze Z:
(AB)(BD)(CF)(DH)(EJ)(FL)(GC)(HP)(IR)(JT)(KX)(LV)(MZ)(NN)(OY)(PE)(QI)(RW)(SG)(TA)(UK)(VM)(WU)(XS)(YQ)(ZO)
Steckerverbindungen:
Q↔P T↔V
A↔S G↔H
W↔Y Z↔B
E↔X U↔N
D↔F J↔K
R↔C I↔M
O↔L
Daten der Walze V des alten Walzensatzes
Transportkerbe 08
01-22 08-25 15-12 22-15
02-26 09-21 16-24 23-06
03-02 10-16 17-01 24-05
04-18 11-19 18-23 25-03
05-07 12-04 19-13 26-11
06-09 13-14 20-10
07-20 14-08 21-17
Arbeitsgebiet 11 Geheime Verschlußsache
MfS 049 Nr. 5364/62
2. Ausfertigung 25 Blatt
Az.: G 604
TEILANALYSE DES VERFAHRENS
ENIGMA
Berlin, den 2. Juli 1962
Ky
Arbeitsgebiet 11
Teilanalyse des Verfahrens ENIGMA
1 Beschreibung des Verfahrens und Aufgabenstellung
1.1 Das vorliegende Verfahren ist ein reinperiodisches Addi-
tionsverfahren mit der sehr großen Periode 262·25 = 16 900
Die Chiffrierung geschieht maschinell auf elektrischer Basis
mittels einer Vielfachwegschalters (Chiffrierwalzenpaket).
Die wesentlichen Bestandteile der Maschine sind:
Tastatur Ta mit den 26 Buchstaben des dt. Alphabets.
Steckerverbindung St, mit ihr kann der Stromlauf
verändert werden.
Chiffrierwalzenpaket: Drei Walzen X, Y, Z sind gegenein-
ander drehbar auf einer Achse gelagert. Beide Seiten jeder
Walze weisen je 26 Kontaktstellen auf, die im Inneren paar-
weise miteinander verbunden sind. Sie können für unsere
Betrachtungen als Permutationen 26-ter Ordnung angesehen
werden (ebenso wie die Steckerverbindungen St).
Umkehrwalze U: Nicht drehbar gelagerte Walze, die
nur auf einer Seite 26 Kontaktstellen aufweist, die paar-
weise miteinander verbunden sind. Diese Walze wendet den
Stromweg. Sie kann als Permutation 26. Ordnung angesehen
werden, die in 13 Zweierzyklen zerfällt.
Die Walzen X, Y, Z und Ũ sind auswechselbar.
Glühlampenfeld Gl: Hier wird der jeweils beleuchtete Buch-
stabe als Chiffreeinheit abgelesen.
Der Stromverlauf (wenn irgendeine Taste der Tastatur ge-
drückt ist) ist folgender:
Ta → St → X → Y → Z → U → Z-1 → Y-1 → X-1 → St-1 → Gl. (1.1)
1.2 In der Teilanalyse dient als mathematisches Hilfswerk die
Theorie der Permutationen. In diesem Punkt sollen die
wichtigsten Formeln sowie ständig benutzte Bezeichnungen
erläutert werden.
Da das Produkt nicht kommutativ ist, muß von Fall zu Fall
erläutert werden, wie es gebildet wird. Eine Permutation
kann als eineindeutige Abbildung einer Menge auf sich
selbst aufgefaßt werden. Unter dem Produkt zweier Permu-
tationen AB verstehen wir die zusammengesetzte Abbildung,
in welcher zuerst A und dann B auftritt, z. B.

Mit n bezeichnen wir immer die Ordnung der Permutationen;
n wird - wenn es von Bedeutung ist - stets als gerade vor-
ausgesetzt da uns der Fall n = 26 interessiert.
Wir benutzen folgende Bezeichnungen:

Wir verwenden weiterhin die Zyklenschreibweise:

Zur Konjugiertenberechnung B-1AB bzw. BAB-1 leistet folgende
offensichtliche Formel oft gute Dienste:
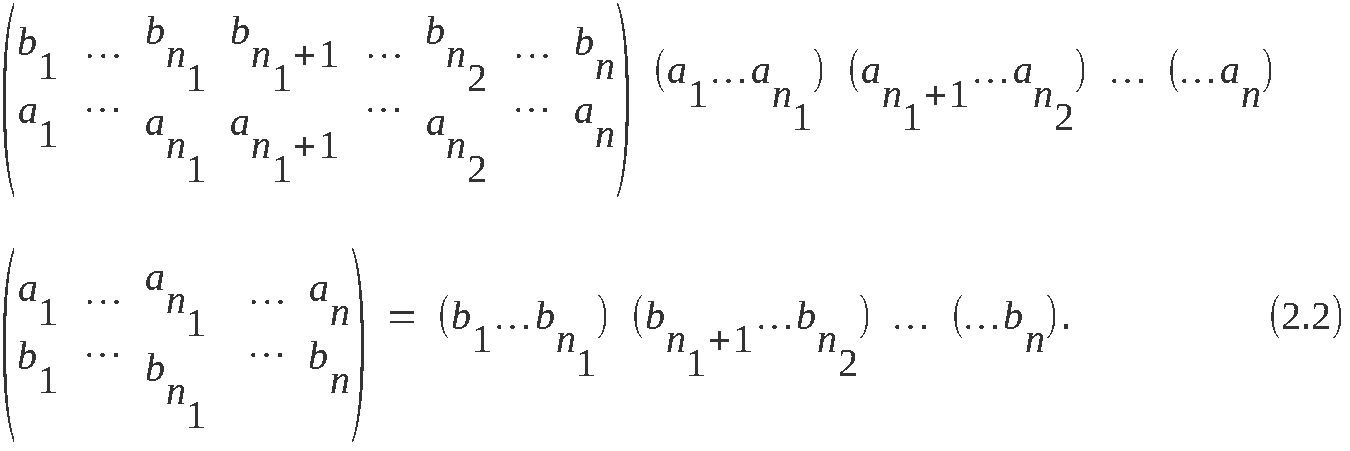
Eine weitere mögliche Schreibweise für  ist folgende:
A:ai→bi (i = 1, 2, i… , n).
Mitunter ist es zweckmäßig, eine Permutation als einein-
deutige Abbildung der Menge der Restklassen (im zahlen-
theoretischen Sinne) modulo n auf sich anzusehen. Es wird
wie folgt verfahren:
Wir lassen als Indexe der Elemente ai sowie als Elemente
selber alle ganzen Zahlen zu und identifizieren
ai + tn (-∞ < t < +∞, 1 ≤ i ≤ n) bzw.
ai + tn (-∞ < t < +∞, 1 ≤ ai ≤ n) mit ai.
Wenn in einer Relation zwischen Permutationen oder deren
Elemente als Elemente außer 1, 2, …, n auch andere
ganze Zahlen auftreten oder auftreten können, so gebrauchen
wir das Zeichen
ist folgende:
A:ai→bi (i = 1, 2, i… , n).
Mitunter ist es zweckmäßig, eine Permutation als einein-
deutige Abbildung der Menge der Restklassen (im zahlen-
theoretischen Sinne) modulo n auf sich anzusehen. Es wird
wie folgt verfahren:
Wir lassen als Indexe der Elemente ai sowie als Elemente
selber alle ganzen Zahlen zu und identifizieren
ai + tn (-∞ < t < +∞, 1 ≤ i ≤ n) bzw.
ai + tn (-∞ < t < +∞, 1 ≤ ai ≤ n) mit ai.
Wenn in einer Relation zwischen Permutationen oder deren
Elemente als Elemente außer 1, 2, …, n auch andere
ganze Zahlen auftreten oder auftreten können, so gebrauchen
wir das Zeichen 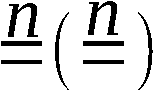 , wenn es sich um Permutationen han-
delt, und die Kongruenzschreibweise der Zahlentheorie oder
das Zeichen
, wenn es sich um Permutationen han-
delt, und die Kongruenzschreibweise der Zahlentheorie oder
das Zeichen  , wenn es sich um Elemente handelt. Wenn
von 1, 2, …, n verschiedene Indexe auftreten, so
behalten wir die gewöhnliche Schreibweise bei.
Im folgenden wird ist T stets die Permutation
, wenn es sich um Elemente handelt. Wenn
von 1, 2, …, n verschiedene Indexe auftreten, so
behalten wir die gewöhnliche Schreibweise bei.
Im folgenden wird ist T stets die Permutation

bezeichnet. Es ist dann
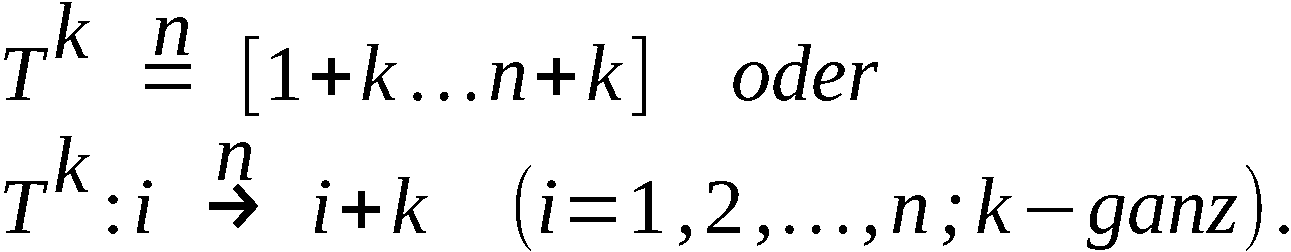
U bedeutet stets eine nur aus Zweierzyklen zusammengesetzte
Permutation.
1.3 Das Schema (1.1) für den Stromverlauf führt zu einer Formel
für die jeweilige Substitution S. Es ist
Skji = St · TkXT-k·U·TkX-1T-k·St-1, (3.1')
mit U = TjYT-j·TiZT-i·Ũ·TiZ-1T-i·TjY-1T-j. (3.1´)
Die Potenz Tk, T-k usw. treten wegen der
Verdrehbarkeit der Chiffrierwalzen gegeneinander auf.
Die Indexe k, j und i geben an, wie weit die Walzen X,
Y und Z gegenüber der Grundstellung verdreht sind.
1.4 Aufgabenstellung
Es ist zu klären, unter welchen Bedingungen gleiche Sub-
stitutionen auftreten können.
Mit anderen Worten: Wann gilt die Gleichen
Sk´j´i´ = Sk´´j´´i´´, (3.2)
wenn nicht gleichzeitig
k´ = k´´, j´ = j´´, i´ = i´´ ? (3.3)
In dieser Form ist das Problem ein rein mathematisches
und soll auch als solches behandelt werden.
Es wurden bisher nur Teilfragen gelöst. Eine umfassende
Antwort auf die aufgeworfene Frage zeichnet sich noch
nicht ab.
2 Vereinfachungen
2.1 Wir setzen St = E = [1 2 … n]. Wegen (3.1) ist bei
festem St genau dann S´ = S´´, wenn St-1S´St = St-1S´´St.
2.2 Wir betrachten in der Teilanalyse nur den Sonderfall
Y = Z = E.
Das Problem lautet dann: Wann gilt die Gleichung
TpXT-p·U·TpX-1T-p = TqXT-q·U·TqX-1T-q ? (4.1)
Diese Gleichung besitzt für beliebige X, p und q immer die
Lösung X = Tr (r - ganz), Umformungen sind also zulässig.
Da gemeinsam mit X auch TrX (r - ganz). die Gleichung löst,
genügt es, die Differenz q-p zu betrachten.
Multiplizieren wir (4.1) von links mit T-p und von rechts
mit Tp, so erhalten wir die Gleichung
X·T-pUTp·X-1 = Tq-pXT-(q-p)·T-p·Tq-pX-1T-(q-p)
Diese Gleichung untersuchen wir in Punkt 3, wo wir aus
Gründen der Zweckmäßigkeit
X durch X-1, T-pUTp durch U, q-p durch k
ersetzen.
Eine andere Gleichung erhalten wir, wenn wir (4.1) von links
mit T-p und von rechts mit Tq multiplizieren:
X·T-pUTp·X-1Tiq-p = T1-pXT-(q-p)·T-p·UTp·Tq-pX-1.
Multiplizieren wir nun von links mit X-1 sowie von
rechts mit XT-(q-p):
T-pUTp·X-1Tq-pXT-(q-p) = X-1Tq-pXT-(q-p)·T-pUTp
Diese Gleichung wird in Punkt 4 untersucht. Es wird
T-pUTp durch U und q-p durch k
ersetzt.
2.3. Wir betrachten nur K = 1, 2, …, n-1, denn es ist
Tk+rn = Tk für r - ganz
sowie
T0 = Tn = E
(in diesem Fall ist die Gleichung (4.1) immer richtig).
3 Untersuchung der Gleichung X-1 UX = (TkXT-k)-1U(TkXT-k)
3.1 Grundlegende Sätze
Wir betrachten die Gleichung
X-1 UX = (TkXT-k)-1U(TkXT-k). (5.1)
Sie X = [a1a2…an], U = (b1b2)…(bn-1bn), 1 ≤ k ≤ n-1.
Sowohl X als auch U als auch k können als zu bestimmende
Unbekannte angesehen werden.
O.B.d.A. können wir, wenn es sinnvoll ist, a1 = 1 setzen. Denn
zugleich mit X sind alle XTr (r - ganz) Lösungen von (5.1),
wie man durch unmittelbares Einsetzen erkennt. Ebenso können
wir o.B.d.A. b1 = 1 setzen.
Die Paare
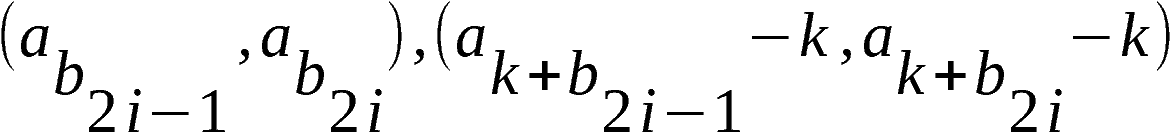
betrachten wir für i = 1, 2, …, m = n/2 als Elemente der Mengen
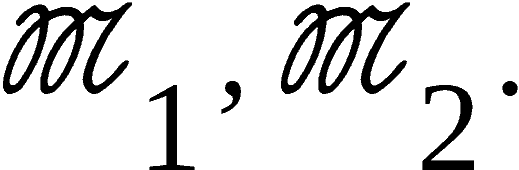
Zwei Paare (a´, a´´) und (a´´, a´) seien gleich, d. h. die
Anordnung innerhalb der Paare möge keine Rolle spielen.
Zwei Mengen nennen wir gleich wenn ihre Elemente zusammen-
fallen.
Es gilt folgender Satz:
S a t z I
Irgendwelche konkreten X, u und k erfüllen genau dann die
Gleichung (5.1) wenn
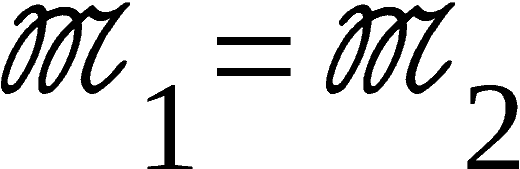
Bilden wir die Permutationen
 (5.2)
(5.2)
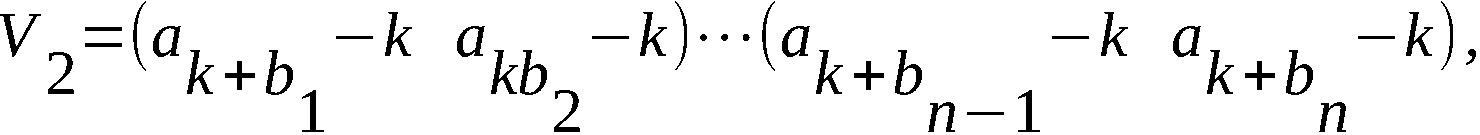 (5.3)
(5.3)
so können wir folgenden Satz formulieren:
S a t z I´
Irgendwelche konkreten X, U und k erfüllen genau dann die
Gleichung (5.1) wenn  .
Wir zeigen zunächst die Äquivalenz beider Sätze.
S a t z II
.
Wir zeigen zunächst die Äquivalenz beider Sätze.
S a t z II 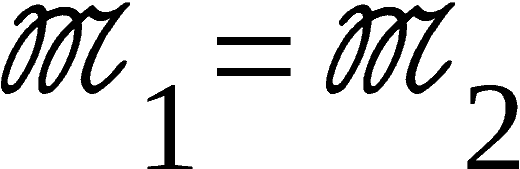 genau dann, wenn
genau dann, wenn  .
Beweis: Zwei Mengen sind gleich, wenn sie elementweise zusam-
menfallen. Die "Mengengleichung"
.
Beweis: Zwei Mengen sind gleich, wenn sie elementweise zusam-
menfallen. Die "Mengengleichung" 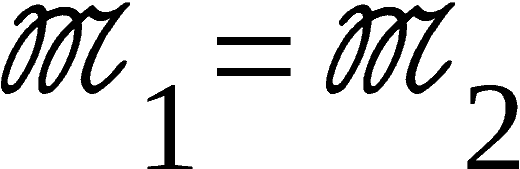 ist also äquivalent
dem Gleichungssystem
ist also äquivalent
dem Gleichungssystem
 (6.1)
(6.1)
wobei i1, i3, …, in-1 eine Permutation der Zahlen 1, 3, …, n-1
bilden.
Wenn das Gleichungssystem gilt, so gilt auch  -
man braucht nur die jeweiligen Zyklen gleichzusetzen.
Umgekehrt, ist
-
man braucht nur die jeweiligen Zyklen gleichzusetzen.
Umgekehrt, ist  , so gilt auch (6.1) - ev. bilden die
i1, i3, … eine von der obigen verschiedene Permutation; denn
wenn zwei Permutationen gleich sind, so sind auch ihre
einzelnen Zyklen gleich.
Wir beweisen nun Satz I: Wegen Satz II ist dann auch Satz I
bewiesen.
Beweis:
a) Betrachten wir zunächst TkXT-k. Es ist
, so gilt auch (6.1) - ev. bilden die
i1, i3, … eine von der obigen verschiedene Permutation; denn
wenn zwei Permutationen gleich sind, so sind auch ihre
einzelnen Zyklen gleich.
Wir beweisen nun Satz I: Wegen Satz II ist dann auch Satz I
bewiesen.
Beweis:
a) Betrachten wir zunächst TkXT-k. Es ist

b) Es ist X:1 → ai oder auch X:bi→ . Unter Ausnutzung
der Formel (2.2) erhalten wir folgnde Beziehung:
. Unter Ausnutzung
der Formel (2.2) erhalten wir folgnde Beziehung:

Wegen (5.2) ist also
X-1UX = V1. (7.1)
c) Unter Ausnutzung von a) und wiederum der Formel (2.2)
erhalten wir:
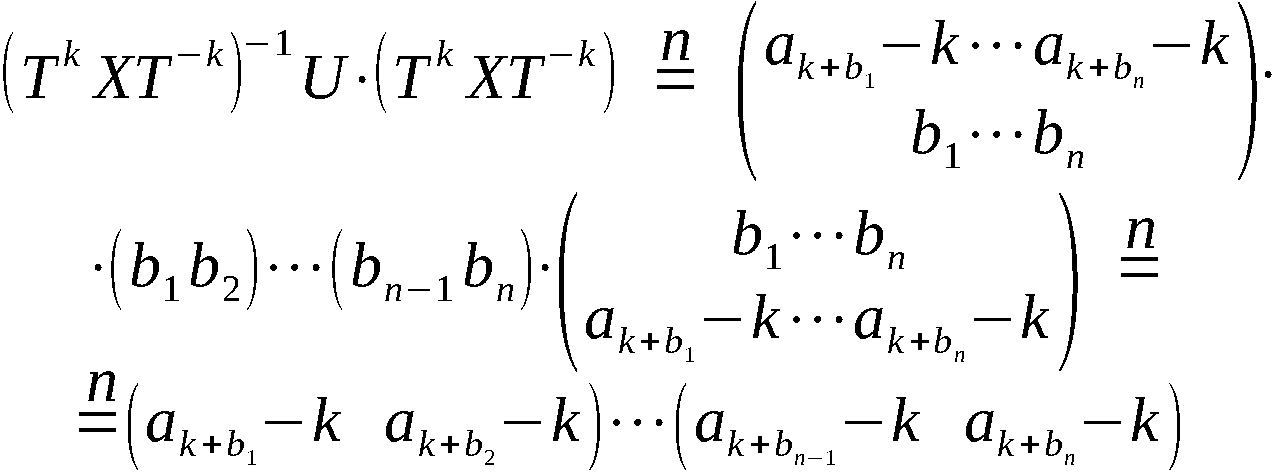
Wegen (5.3) gilt also die Beziehung
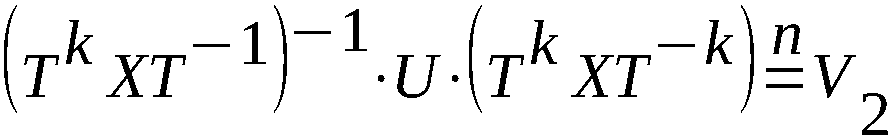 (7.2)
(7.2)
d) Die Formeln (7.1) und (7.2) zeigen die Richtigkeit der
zu beweisenden Behauptung.
Im weiteren benötigen wir noch die Mengen

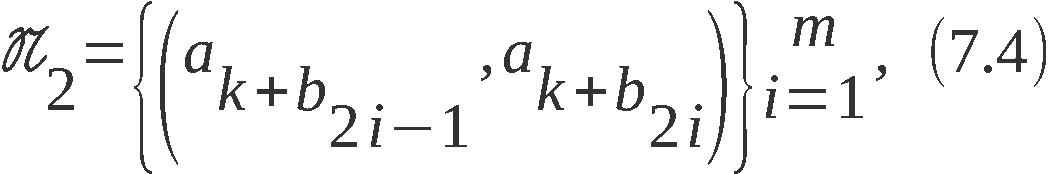
sowie die Permutationen
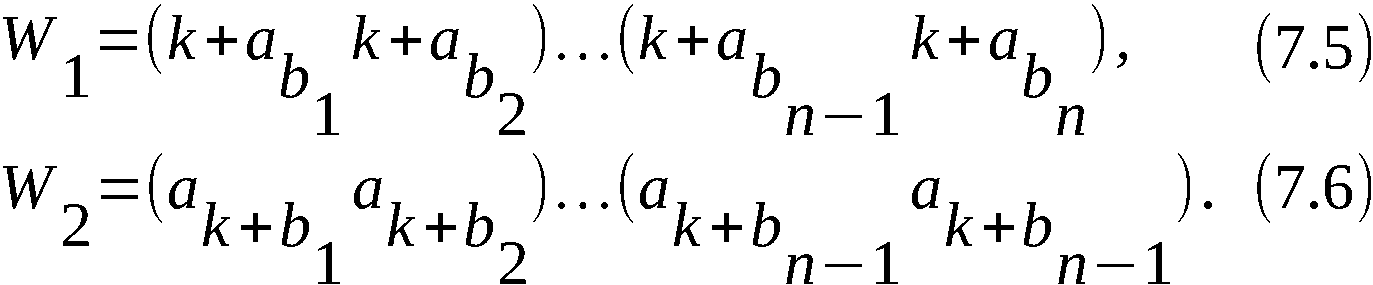
S a t z III

Beweis: Wir betrachten wieder das Gleichungssystem (6.1) und
in ihm (z. B.) die erste Gleichung
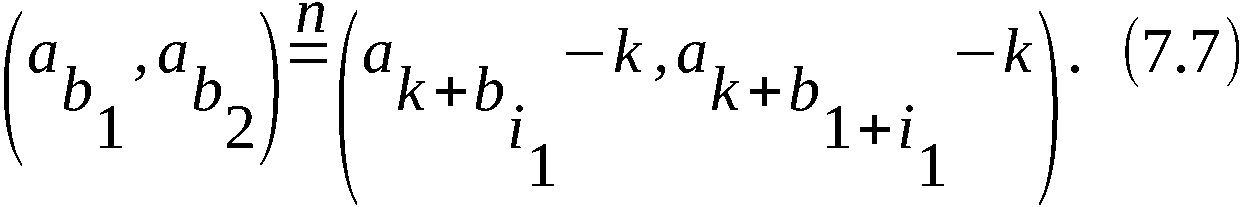
Diese Beziehung ist gleichbedeutend mit

Auf beiden Seiten einer Kongruenz kann man gleiche Zahlen
addieren. Das tun wir in (8.1) mit dem Summanden "+k". Dann
sehen wir, daß die Kongruenzen (8.1) gleichbedeutend sind
mit der Beziehung
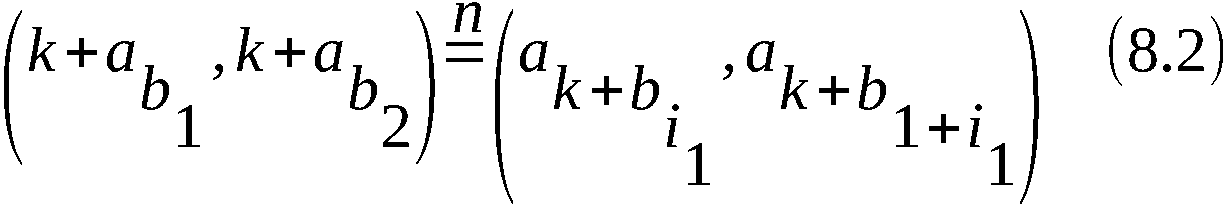
(7.7) und (8.2) sind also äquivalent.
Auf die gleiche Art und Weise lassen sich die anderen Glei-
chungen des Systems (6.1) umformen. Damit ist der Satz im
wesentlichen bewiesen. Der Rest folgt nach der Linie des
Beweises zu Satz II.
Die in diesem Punkt bewiesenen Sätze gestatten die Angabe
von Algorithmen zur Bestimmung der Lösung der Gleichung
(5.1). Bevor wir hierzu übergehen, fassen wir noch einmal
zusammen:
S a t z IV
folgende Aussagen sind gleichbedeutend:
1. Die Gleichung (5.1) ist erfüllt,
2. 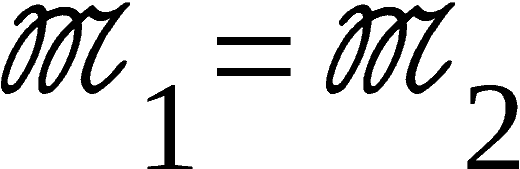 ,
3.
,
3. 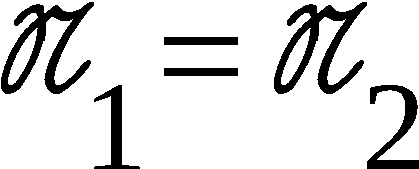 ,
4.
,
4.  ,
5.
,
5.  .
3.2 Ein Algorithmus zur Bestimmung lösender k
Wir geben nun einen Algorithmus an, der es gestattet, bei
festen U und X eventuell vorhandene lösende K der Gleichung
(5.1) zu finden. Wir stützen uns dabei auf die Sätze I und II
und gehen vom Gleichungssystem (6.1) aus. Für n führt
der Algorithmus vermutlich schneller zum Ziel als direktes
Einsetzen aller k in (5.1) und Ausrechnen. Ein erläuterndes
Beispiel folgt im Anschluß an die Darlegung.
Die Frage, ob sich aus dem vorliegenden Algorithmus weitere
Gesetzmäßigkeiten über die Lösung der Gleichung (5.1)
gewinnen lassen, wurde aus Zeitmangel offengelassen. Sie
verdient meines Erachtens Aufmerksamkeit.
Kommen wir nun zum Algorithmus selber, der in m Schritte
zerfällt:
1.) Die erste Gleichung des Systems (6.1) lautet
.
3.2 Ein Algorithmus zur Bestimmung lösender k
Wir geben nun einen Algorithmus an, der es gestattet, bei
festen U und X eventuell vorhandene lösende K der Gleichung
(5.1) zu finden. Wir stützen uns dabei auf die Sätze I und II
und gehen vom Gleichungssystem (6.1) aus. Für n führt
der Algorithmus vermutlich schneller zum Ziel als direktes
Einsetzen aller k in (5.1) und Ausrechnen. Ein erläuterndes
Beispiel folgt im Anschluß an die Darlegung.
Die Frage, ob sich aus dem vorliegenden Algorithmus weitere
Gesetzmäßigkeiten über die Lösung der Gleichung (5.1)
gewinnen lassen, wurde aus Zeitmangel offengelassen. Sie
verdient meines Erachtens Aufmerksamkeit.
Kommen wir nun zum Algorithmus selber, der in m Schritte
zerfällt:
1.) Die erste Gleichung des Systems (6.1) lautet
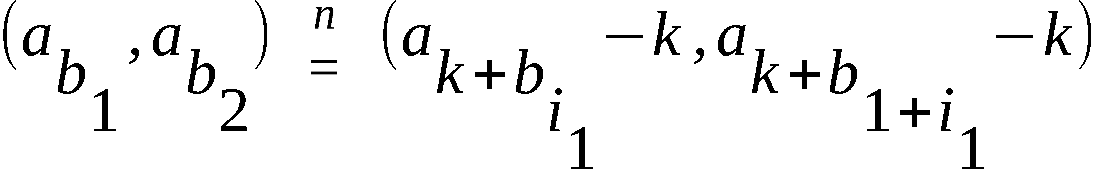 (9.1)
(9.1)
Diese Gleichung ist äquivalent dem System
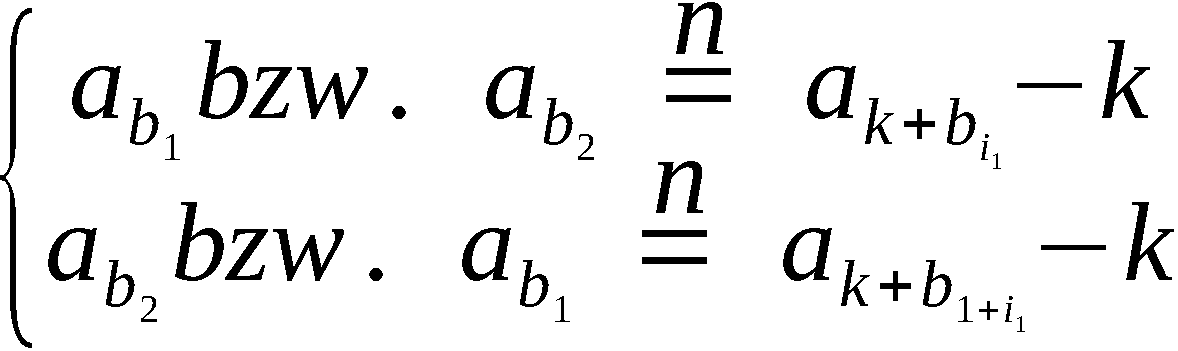
in welchem die linken Seiten bekannt sind, da laut Voraus-
setzung U und X fest vorgegeben sind.
Wir probieren nun zunächst in der ersten Gleichung dieses
Systems alle zugelassenen i1 und k der Reihe nach durch.
Ist die Gleichung nicht erfüllt, so können diese Werte keine
Lösung ergeben - ist sie erfüllt, so ist die zweite
Gleichung nachzuprüfen.
Unsere Ergebnisse fixieren wir in einer Tabelle:
| i1\ | k | 1 | 2 | … | n-1 |
| 1 | x | x | … | + |
| 3 | + | x | … | x |
| … | … |
| n-1 | x | x | … | x |
| Tab. 1 "+" lösend; "x" nicht lösend |
Nach Auffüllung der Tab. 1 gehen wir zum nächsten Schritt
über
2.) Wir verfahren wie eben, nur nehmen wir anstelle der
ersten Gleichung des Systems (6.1) und die zweite.
Es ergeben sich jetzt einige Vereinfachungen:
a) In der Tab. 2 können wir die Spalte weglassen,
welche in der vorherigen Tabelle nur Kreuze (x)
enthalten. Denn ein solches k kann eine Lösung der
Gleichung (5.1) sein, weil es kein i1 gibt, welches
es Gleichung (9.1) löst.
b) In Tab. 2 können wir in die Felder sofort ein Kreuz
eintragen, welche in Tab. 1 ein "+" enthalten.
Denn i1 = i3 bei gleichem k ist nicht zulässig, da
die i1, i3, …, in-1
eine Permutation der Zahlen 1, 3, …, n-1 bilden.
Siehe Punkt 5
……
m) Der m.Schritt (m=n/2) ist der letzte.
Die zu lösende k sind aus Tabelle m zu ersehen. Es
sind diejenigen, die in der betreffenden Spalte ein "+"
aufweisen.
Beispiel: U = (14)(26)(35) ≡ (b1b2)(b3b4)(b5b6);
X = [164523] ≡ [a1a2a3a4a5a6]
| i1\ | k | 1 | 2 | 3 | 4 | 5 |
| 1 | + | x | x | x | x |
| 3 | x | x | + | + | x |
| 5 | x | x | x | x | x |
| Tab. 1 |
1.)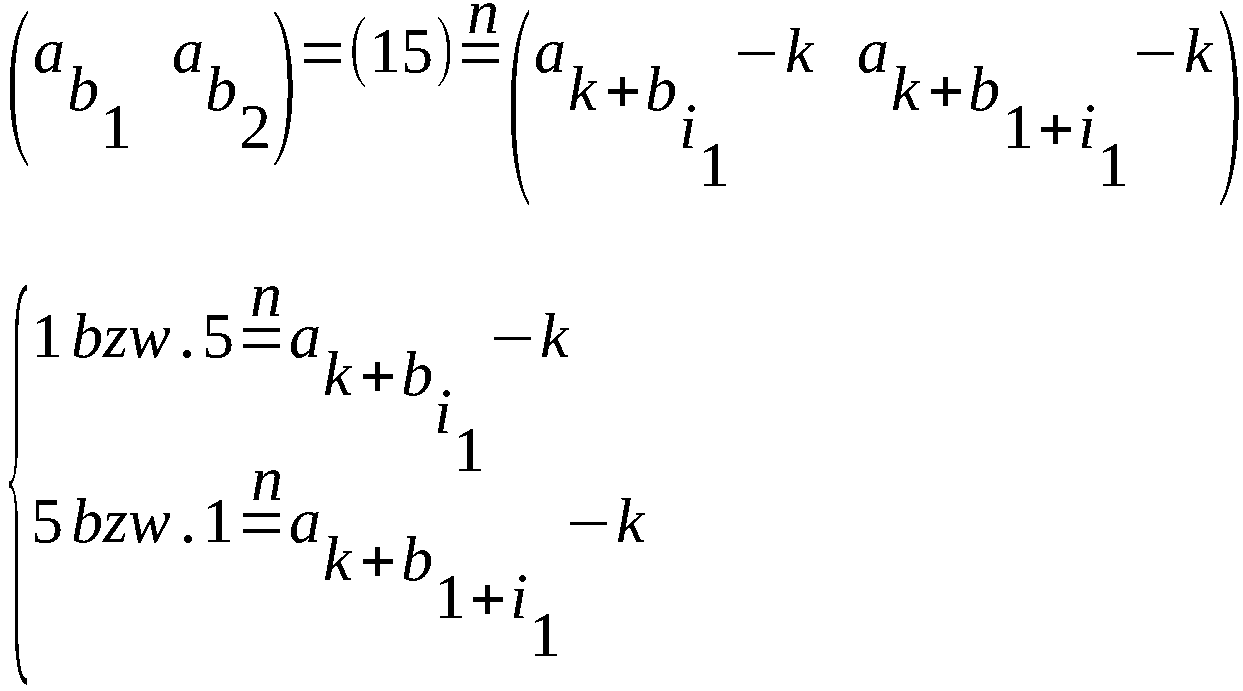
| i1 | bi1 | k | k+bi1 = j | aj | aj-k | // | 1+i1 | b1+i1 | k+b1+i1 = l | al | al-k |
|---|
| 1 | 1 | 1 | 2 | 6 | 5 | | 2 | 4 | 5 | 2 | 1 |
| | 2 | 3 | 4 | 2 | | | | | |
| | 3 | 4 | 5 | 2 | | | | | |
| | 4 | 5 | 2 | 4 | | | | | |
| | 5 | 6 | 3 | 4 | | | | | |
| 3 | 2 | 1 | 3 | 4 | 3 | | | | | |
| | 2 | 4 | 5 | 3 | | | | | |
| | 3 | 5 | 2 | 5 | 4 | 6 | 3 | 4 | 1 |
| | 4 | 6 | 3 | 5 | 4 | 6 | 4 | 5 | 1 |
| | 5 | 1 | 1 | 2 | | | | | |
| 5 | 3 | 1 | 4 | 5 | 4 | | | | | |
| | 2 | 5 | 2 | 6 | | | | | |
| | 3 | 6 | 3 | 6 | | | | | |
| | 4 | 1 | 1 | 3 | | | | | |
| | 5 | 2 | 6 | 1 | 6 | 5 | 4 | 5 | 6 |
2.)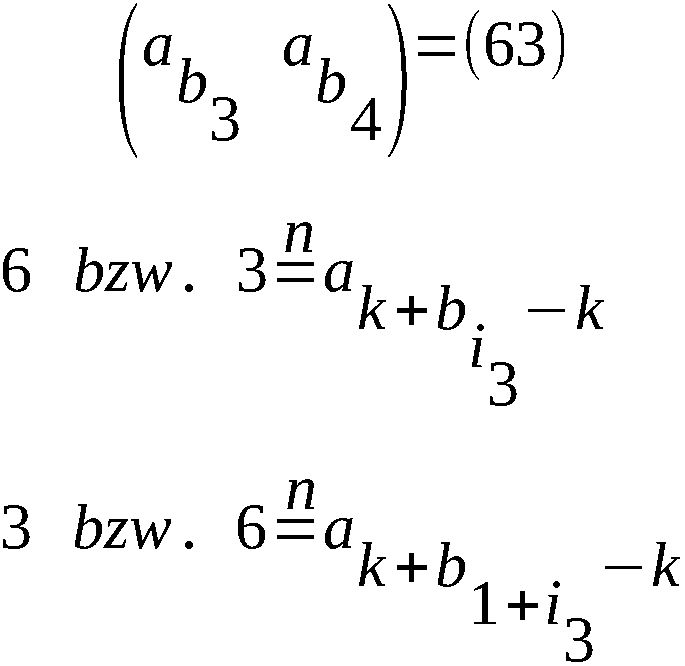
| i3\ | k | 1 | 3 | 4 |
| 1 | x | x | x |
| 3 | + | x | x |
| 5 | x | + | + |
| Tab. 2 |
| i3 | bi3 | k | k+bi3 = j | aj | aj-k | // | 1+i3 | b1+i3 | k+b1+i3 = l | al | al-k |
|---|
| 1 | 1 | 3 | 4 | 5 | 2 | | | | | | |
| | 4 | 5 | 2 | 4 | | | | | |
| 3 | 2 | 1 | 3 | 4 | 3 | 4 | 6 | 1 | 1 | 6 |
| 5 | 3 | 1 | 4 | 5 | 4 | | | | | |
| | 3 | 6 | 3 | 6 | 6 | 5 | 2 | 6 | 3 |
| | 4 | 1 | 1 | 3 | | | 3 | 4 | 6 |
3.)
| i3\ | k | 1 | 3 | 4 |
| 1 | x | x | x |
| 3 | x | x | x |
| 5 | + | x | x |
| Tab. 3 |
| i5 | bi5 | k | k+bi5 = j | aj | aj-k | // | 1+i5 | b1+i5 | k+b1+i5 = l | al | al-k |
|---|
| 1 | 1 | 3 | 4 | 5 | 2 | | 2 | 4 | 1 | 1 | 4 |
| | 4 | 5 | 2 | 4 | | | 2 | 6 | 2 |
| 5 | 3 | 1 | 4 | 5 | 4 | 6 | 5 | 6 | 3 | 2 |
Die Gleichung (5.1) ist also für k = 1, 3, 4 erfüllt.
3.3 Über die Bestimmung lösender X der Gleichung (5.1)
Wir halten nun U und k fest und suchen die Gleichung (5.1)
lösende X.
Wie in 3.1 gezeigt wurde, ist die Gleichung (5.1) genau dann
gelöst, wenn
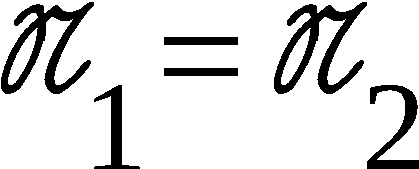
bzw.

Es muß also das Gleichungssystem

erfüllt sein, wobei i1, i3, …, in-1 irgend eine Permutation
der Zahlen 1, 3, …, n-1 bilden.
Betrachten wir wieder als Beispiel die erste Gleichung
des Systems (12.1). Für jedes i1, i3, …, in-1 gibt es zwei
Möglichkeiten:

Diese Gleichungen stellen Beziehungen zwischen verschiedenen
a aus X = a1 … an dar, denen X genügen muß, um Lösung zu sein.
Jede der m Gleichungen des Systems (12.1) liefert zwei Paar
solcher Beziehungen, von denen ein Paar erfüllt sein muß. Bei
fester Permutation i1, …, in-1 liefert !2.1) also 2m
Gleichungssysteme n-ter Ordnung mit den Unbekannten a1, …, an
(die nicht unbedingt alle in jedem System aufzutreten brauchen).
Da es m! verschiedene Permutationen der i1, …, in-1
gibt, gälte es,
m! * 2m
Gleichungssysteme n-ter Ordnung mit n Unbekannten zu lösen.
Wenn die Gleichung (5.1) erfüllt ist, so ist auch eines dieser
Systeme erfüllt und umgekehrt: Ist eines dieser Systeme erfüllt
und gehören alle Lösungen voneinander verschiedenen Restklassen
mod n an, so ist auch (5.1) erfüllt.
Die Untersuchung dieser Systeme mit Methoden der in der Mathe-
matik weitverbreiteten und verzweigten Matrizentheorie wurde
aus zeitlichen Gründen nicht vorgenommen. Sie würde sicher-
lich interessante Resultate zeigen. Eine Vereinfachung besteht
darin, daß - bei beliebigem n - in jeder Zeile der Matrix des
Systems nur ein oder zwei von 0 (Null) verschiedene Elemente
auftreten.
3.4 Ein Algorithmus zur Bestimmung lösender X
Von (12.1) ausgehend, läßt sich auch hier wieder ein Al-
gorithmus angeben. Verglichen mit 3.2, wo sich die Rechnung
von Schritt zu Schritt vereinfachte, ist es hier umgekehrt.
Die Anzahl der lösenden X ist im allgemeinen bedeutend
größer als die der lösenden k.
1.) Wir nehmen wieder die erste Gleichung des Systems (12.1)
her, aus der wir 2m Gleichungspaare der Art 12.2) bzw.
(12.3) erhalten. Wir suchen die Paare, welche einen
Widerspruch aufweisen, und schließen sie aus der weiteren
Betrachtung aus. n
(Z. B. wäre die Gleichung k+a2 = a2 ein Widerspruch, da
wir nur k = 1, 2, …, n-1 betrachten).
2.) Aus der zweiten Gleichung des Systems (12.1) erhalten wir
wiederum 2m Gleichungspaare. Zuerst untersuchen wir die
Paare auf Widerspruchsfreiheit und werfen die widersprüch-
lichen fort. Dann kombinieren wir die Paare mit den aus 1.)
übriggebliebenen zu Systemen 4. Ordnung - die Anzahl der
Kombinationen ist wegen i1 ≠ i3 höchstens gleich 2m*2(m-1)
und untersuchen diese auf Widerspruchsfreiheit. Dazu sind
paarweise die Gleichungen, die wir aus der zweiten Glei-
chung des Systems (12.1) erhielten, mit den Gleichungen,
die wir aus der ersten Gleichung erhielten, zu verglei-
chen. Das erfordert 4 Vergleiche in jedem der Systeme
4. Ordnung.
3.) Aus der dritten Gleichung des Systems (12.1) erhalten
wir erneut 2m Gleichungspaare, von denen wir die wider-
sprüchlichen entfernen. Dann kombinieren wir die Paare
aus den aus 2.) übriggeblieben Systemen 4. Ordnung zu
Systemen 6. Ordnung. Die Anzahl der Kombinationen ist
wegen i1 ≠ i3 ≠i5 ≠i1 höchstens gleich 23*m(m-1)(m-2). Die
Systme 6. Ordnung untersuchen wir auf Widerspruchsfreiheit,
indem wir paarweise die Gleichungen, die wir aus der
dritten Gleichung des Systems (12.1) erhielten, mit den
Gleichungen, die wir aus 2.) erhielten, vergleichen. Das
erfordert 8 Vergleiche in jedem der Systeme.
……
m.) der m. Schritt ist der letzte.
Für die Charakterisierung der Güte des Algorithmus von
Bedeutung ist die Frage nach einer Abschätzung der Anzahl
der in jedem Schritt wegen Widersprüchlichkeit fortfallenden
Systeme. Diese Frage ist nicht untersucht worden. Eine
brauchbare Antwort ist vermutlich nicht leicht zu finden.
3.5 Ebenso wie in 3.2 und 3.4 ließe sich vielleicht auch ein
Algorithmus zur Bestimmung lösender U der Gleichung (5.1)
bei festen X und k finden. Diese Frage wurde nicht betrachtet.
Es ist vorstellbar, daß für bestimmte U und X die Gleichung
(5.1) keine lösenden k besitzt (das hieße, die Gleichung
(4.1) wäre nicht lösbar). Ein Herangehen an das Problem von
dieser Seite mittels des in 3.2 aufgezeigten Algorithmus
oder auf anderem Wege verdient eventuell Beachtung.
4 Untersuchung der Gleichung X-1TkTX-k·U = U·X-1TkXT-k
In diesem Punkt untersuchen wir die Gleichung
FU = UF (15.1)
mit F = Fk(X) = X-1TkXT-k (15.2)
Diese Gleichung ist - ebenso wie die im vorigen Punkt unter-
suchte - äquivalent der Gleichung (4.1). Trotz gegenteiliger
Vermutungen erbrachte die Untersuchung der Gleichung (15.1)
jedoch weniger Resultate als die Gleichung (5.1).
4.1 H i l f s s a t z Seien A und B zwei beliebige vertauschbare
Permutationen,d. h.
AB = BA.
Dann sind auch Ar (r-ganz) und Bs (s-ganz) vertauschbar:
ArBs = BsAr.
Dieser Fakt hat Allgemeingültigkeit sogar in der Gruppen-
theorie und wird deshalb nicht bewiesen. Als Beweismittel
dient die mathematische Induktion in der Gleichung B = A-1BA,
zunächst in r bei s = 1, dann in s bei festem r.
Es ergeben sich hieraus einige Schlußfolgerungen für die
Gleichung (15.1). Bemerken wir zuvor noch, daß
U-1 = U und U2 = E
gilt, da U nur aus Zweierzyklen besteht.
S a t z I Die Gleichung (15.1) ist genau dann erfüllt, wenn
TkX-1T-kXU = UTkX-1T-kX.
Beweis: Es ist
F-1 = (X-1)TkXT-k)-1 = TkX-1T-kX.
S a t z II Seien F1 und F2 Lösungen der Gleichungen (15.1)
bei festem U. Dann sind alle Elemente der von F1 und F2
erzeugten Untergruppe ebenfalls Lösungen der Gleichung (15.1).
Beweis: Die Elemente der Untergruppe habe die Form

r und s - ganz, i - nat. Zahl.
Laut Voraussetzung gilt
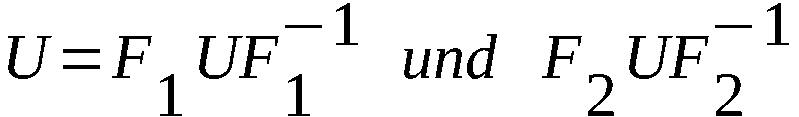
O.B.d.A. (wegen i < ∞) führen wir den Beweis für das Element

Der Fall q ≤ 0 ist entsprechend zu behandeln.
Bemerkung: Der Satz läßt sich auf offensichtliche Art und
Weise verallgemeinern, wenn die Gleichung (15.1) bei festem
U die Lösungen F1, F2, …, Fj (j - nat. Zahl) besitzt.
S a t z III Seien U1, U2, …, Uj - Lösungen der Gleichung
(15.1) bei festem F. Dann sind alle Elemente der von U1, …, Uj
erzeugten Untergruppe ebenfalls Lösungen.
Der Beweis verläuft wie in Satz II, wobei zu bemerken ist, daß
wegen U2 = E - die Elemente der Untergruppe die Form haben

wo alle r nur die Werte 0 oder 1 annehmen können.
4.2 S a t z IV Alle Lösungen der Gleichung XTk = TkX sind
auch Lösungen der Gleichung (15.1) für beliebiges U.
Beweis: Es ist
F = X-1TkXT-k = X-1XTkT-k = E.
Über die Gleichung XTk = TkX wird demnächst eine Wissen-
schaftliche Abhandlung des Verfassers der Teilanalyse beendet.
In ihr werden u. a. Algorithmen zur Lösung dieser Gleichung
angegeben.
Bemerkung 1: Alle Lösungen der Gleichung XTk = TkX sind für
beliebiges U Lösungen der Gleichung (q - ganz)
Fqk(X)U = UFqk(X).
Das folgt aus dem Hilfssatz (4.1) und Satz IV.
Folgerung 2: Alle Lösungen der Gleichung XTk = TkX sind für
beliebiges U Lösungen der Gleichung Fz(X)U = UFz(X), wenn
ein solches q- ganz existiert, daß
z ≡ qk (mod n) (17.1)
Beweis: (17.1) heißt: Es existiert ein t - ganz mit
z+tn = qk (17.2)
Nun ist aber
Tz = Tz+tn = Tqk
und es bleibt Folgerung 1 anzuwenden.
Offenbar ist
Z ≡ 0 (mod d),
wobei d = (n,k) der größte gemeinsame Teiler der Zahlen n und k
sein möge. Das folgt aus (17.2).
4.3 S a t z V Löst X die Gleichung (15.1), so löst auch alle TrX
(r - ganz) diese Gleichung.
Beweis: Es ist
Fk(TrX) = Fk(X),
wie man aus (15.2) erkennt.
Sei Hk(X) = X-1TkX = Fk(X)Tk.
Wenn X alle n! Permutationen durchläuft, so durchläuft Hk(X)
Permutationen mit der gleichen Zyklenstruktur wie Tk.
Es gibt also X' ≠ X'' mit
Hk(H') = Hk(H'').
Das gilt z. B. für X und TrX. Berechnungen im Falle n = 6
zeigten, daß es auch noch andere solche Paare gibt.
Die Frage kann man auch in folgender Form stellen:
Es sind die Lösungen der Gleichung
X-1TkX = Y
bei fest vorgegebenen k und Y zu finden. Das Problem wurde
nicht näher betrachtet. Es stellt eine Verallgemeinerung
des Problems dar, die Lösungen der Gleichung XTk = TkX
zu finden.
Interessant ist hier folgendes: Die Gleichung

ist genau dann erfüllt, wenn die Gleichung XTk = TkX gilt
für
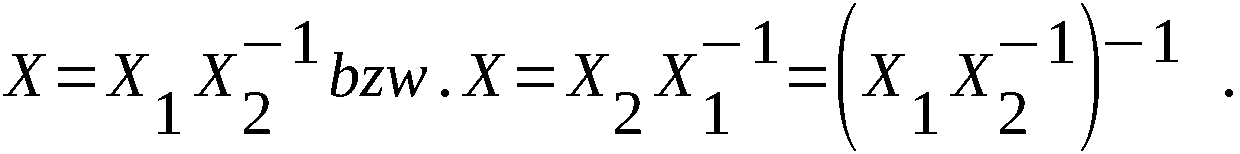
4.4 Man kann zeigen, daß die Permutationen F immer gerade sind.
Der Beweis benutzt elementare Begriffe der Theorie der Per-
mutationen und soll hier nicht angeführt werden, da diese
Eigenschaft von F für uns nur von geringem Interesse ist.
Wir skizzieren nur kurz die Idee: Zunächst wird gezeigt, daß
X-1TkX genau dann gerade bzw. ungerade ist, wenn Tk gerade
bzw. ungerade ist. Weiter läßt sich nachweisen, daß Tk und T-k
gleichzeitig gerade bzw. ungerade sind. Und schließlich ist
das Produkt zweier gerader bzw. ungerader Permutationen
immer gerade.
4.5 Für N = 6 wurden alle möglichen F berechnet und untersucht,
für welche U sie Lösungen darstellen. Es zeigte sich eine
Reihe von Gesetzmäßigkeiten, die nicht allgemein bewiesen
werden konnten. Wir führen einige der wichtigsten an:
a) Wenn F ≠ E für irgendein U Lösung der Gleichung (15.1)
ist, so tritt es für insgesamt genau drei verschiedene
U als Lösung auf.
b) Ist Fk(X) - lösend, so ist Fk(X-1) ebenfalls lsöend,
aber für andere U.
c) Ist Fk(X) - lösend, so ist Fn-k(X) ebenfalls lösend,
aber für andere U.
d) Für K = n/2 gibt es zu jedem X ein U, so daß (15.1) erfüllt
ist; für alle k ≠ n/2 gibt es eine Reihe von X, die für kein
U die Gleichung (15.1) erfüllen.
e) Löst X (15.1) für bestimmte k und U, so löst es auch die
Gleichung für n-k (wobei die U andere sind).
f) Löst X (15.1) für bestimmte k und U, so löst X-1 die
Gleichung für dieselben k (wobei die U andere sind).
g) Die verschiedenen U, die (15.1) bei festen X und k lösen,
zeigen gewisse gemeinsame Merkmale bezüglich der Anzahl
und Art der auftretenden Sequenzen.
Es wurde versucht, mit einfachen Methoden der Gruppentheorie
Ergebnisse zu erzielen. Das führte zu keinem Erfolg.
4.6 Einige prinzipielle Aussagen über Gleichungen der Art (15.1)
werden in der bereits erwähnten Wissenschaftlichen Abhandlung
enthalten sein.
5 Der allgemeine Fall Y ≠ E, Z ≠ E
Das Problem in der allgemeinen Form, wie es in 1.4 formu-
liert wurde, ist nicht untersucht worden. Meiner Ansicht
nach unterscheidet es sich von dem "eindimensionalen"
Fall (Y=Z=E) nur quantitativ, jedoch nicht qualitativ.
Setzen wir in (3.1')

sowie in (3.1) St = E, so sehen wir, daß die Art der Abhän-
gigkeit der Substitution Skji in (3.1) von den Argumenten
X, k, U dieselbe ist wie die der Permutation U in (3.1') von
den Argumenten Y, j, U'. Alle Gesetzmäßigkeiten bezüglich (3.1)
sind auch Gesetzmäßigkeiten bezüglich (3.1').
6 Korrektur eines Fehlers
Beim Überprüfen wurde in dem in 3.2 angegebenen Algorithmus,
Bemerkung b) zum 2. Schritt (siehe 3.2), folgender Fehler
festgestellt, der aber keinen prinzipiellen Einfluß auf die
Durchführbarkeit des Algorithmus hat:
Die angeführte Vereinfachung ist nur zulässig, wenn in der
gegebenen Spalte der Tab. 1 nur ein "+" enthalten ist.
Im gegenteiligen Fall sind alle Kombinationsmöglichkeiten
zu betrachten, wobei nur i1 ≠ i3 beachtet werden muß.
Krey
Ultn.
Arbeitsgebiet II Berlin, den 05.09.1962
Hü, - Anhang I zu
GVS 5384/62
Stellungnahme zur Teilanalyse des Verfahrens ENIGMA
Mit den Ausführungen der Teilanalyse einverstanden.
Der in 3.2 angegebene Algorithmus zur Bestimmung der die
Gleichung
X-1 UX = (TkXT-k)U(TkXT-k).
bei festem X und U lösenden k kann vereinfacht werden.
Da X und U bekannt sind, sind auch 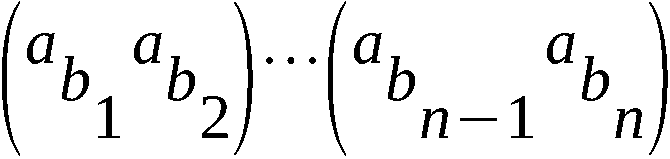 bekannt.
Man benutzt nun die rechte Seite der ersten Gleichung des
Systems (6.1) und setzt o.B.d.A. i1 = 1, d. h. b1.
Man erhält
bekannt.
Man benutzt nun die rechte Seite der ersten Gleichung des
Systems (6.1) und setzt o.B.d.A. i1 = 1, d. h. b1.
Man erhält

Für beliebiges k gilt nun 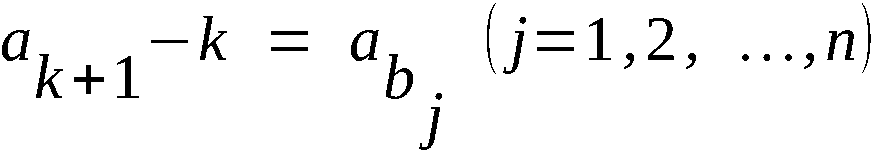 .
Wenn für das gleiche k
.
Wenn für das gleiche k
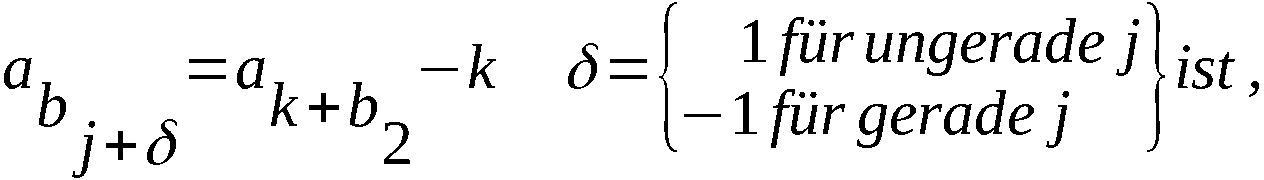
dann kann k eine Lösung (5.1) sein. Ist dies nicht der Fall,
so ist dieses k keine Lösung.
Dies führt man für alle k = 1, 2, …, n-1 durch. Für die nach diesem
Schritt noch möglichen k rechnet man das gleiche mit i1=3 durch.
Ergeben sich hier für irgendwelche dieser k keine Lösungen, so
scheiden diese dann für die weiteren Betrachtungen aus. Für die
danach verbliebenen k wird dann i1=5 gesetzt usw.
Die nach n/2-1 Schritten verbliebenen k sind Lösungen der Gleichung
(5.1).
Beispiel:
U = (14)(26)(35)
X = [134526]
X-1·U·X = (15)(24)(36)
1 2 3 4 5
i1 1 (21) (24) (24) (45) (16)
3 x (31) (51) x x
Als Lösung der Gleichung 5.1 ergibt sich in diesem Beispiel
k = 3.
Hübler
Ltn.
Arbeitsgebiet 1A5 Berlin, den 08.03.1968
Az.: G 604
Tgb.Nr. 1219/68
Chiffriergeräte ENIGMA
Mathematische Darstellung der Chiffrierung
1. Bibliografie
(1) Teilanalyse ENIGMA, 1959, 8 Blatt
(2) Teilanalyse ENIGMA, 2.7.1962, 21 Blatt, GVS 5384/62
(3) Wissenschaftliche Abhandlung Nr. 21 (Leitfaden), 1959.
2. Aufgabenstellung
Das Chiffriergerät ENIGMA ist kryptologisch der Vorläufer
verschiedener in der Gegenwart in Gebrauch befindlicher
Chiffriertechnik des soz. und des kap. Lagers. Analysen
dieser Geräte bauen auf den Analysen von ENIGMA auf.
(Daraus folgt die Notwendigkeit der Geheimhaltung tief-
gründiger analytischer Untersuchungen zu ENIGMA).
Bisher wurden im ZCO nur Einzeluntersuchungen zu ENIGMA
durchgeführt, vgl. Bibliografie. Es erfolgte aber noch
keine systematische mathematisch - kryptologische Beschrei-
bung und Untersuchung von ENIGMA. Das soll mit dem vorlie-
gendem Schriftstück eingeleitet werden.
Das Endziel ist die kryptoanalytische Beherrschung der mo-
dernen Geräte, die aus ENIGMA hervorgegangen sind.
3. Algorithmus
3.1 Mathematische Grundlagen
Mathematisches Hilfsmittel ist die Theorie der endlichen Per-
mutationen und Permutationsgruppen, deren Grundlage im weiteren
vorausgesetzt werden.
Mit n bezeichnen wir die Ordnung der Permutation, mit Sy(n)
die symmetrische Gruppe n-ten Grades aller Permutationen n-ter
Ordnung. n ist eine natürliche Zahl (n = 1, 2, 3, …). Wo es von
Bedeutung ist, wird n stets stillschweigen als gerade vorausge-
setzt, wenn nicht ausdrücklich das Gegenteil festgelegt wird.
Wir benutzen folgende Bezeichnungen zur Darstellung einer
Permutation: Für die allgemeine Darstellung
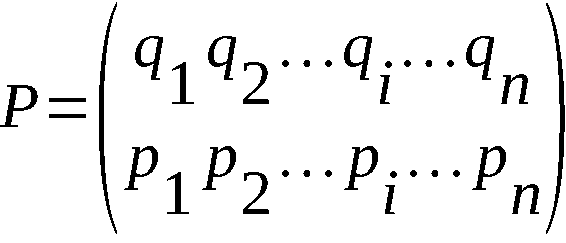
schreiben wir auch
P: qi → pi.
Für P: i → pi schreiben wir auch
P = ((p1 p2 … pi … pn))
Und schließlich wird die Zyklenschreibweise benutzt (jedes
der n Elemente von P tritt in allen Zyklen zusammengenommen
genau einmal auf):

Sei mit R(n) der Restklassenring modulo n mit den Zahlen 1,2, …
…, n als Elementen (n als Nullelement des Rings) bezeichnet.
Betrachten wir die Permutationen als eineindeutige Abbildung
von R (n) auf sich, so führt die folgende Verfahrensweise zu
Vereinfachungen: Als Indexe der Elemente pi sowie alle Elemente
selber lassen wir alle ganzen Zahlen zu und identifizieren
pi-tn = pi + tn = pi
(-∞ < t < +∞, 1 ≤ i ≤n, 1 ≤pi ≤ n).
3.2 Algorithmus
Wir geben hier eine vollständige Beschreibung eines Algorithmus
in abstrakter Form. Im weiteren wird gezeigt, daß bestimmte
Varianten von ENIGMA diesen Algorithmus realisieren.
Die völlige Formalisierung ermöglicht die mathematische Formu-
lierung und Behandlung der kryptologischen Probleme einschließ-
lich der Benutzung elektronischer Rechentechnik.
In unserer Formulierung des Begriffs Algorithmus stützen wir
uns auf das Mathematische Wörterbuch, Berlin - Leipzig, 1961.
Danach ist ein ein Algorithmus in einer Menge von Zeichenreihen
aus gegebenen Grundzeichen als ein Verfahren definiert, mit
dessen Hilfe eine effektive (schrittweise) Umformung der Zeichen-
reihen in endlich vielen Schritten feststellen kann, ob sie
aus einen gegebenen Zeichenreihe durch Anwendung des Algorithmus
erhalten werden kann oder nicht.
Wir geben uns als Grundmenge R(26) vor und betrachten belie-
bige Folgen beliebiger (endlicher) Länge
K = {k1, k2, …. kj, … km};
m ist die Länge der Folge (m = 1, 2, 3, …); kj ∈ R(26) für alle
j = 1, 2, …, m.
Auf R(26) betrachten wir die Permutationsgruppe Sy(26) und
geben uns sechs Elemente T, U, V, X, Y, Z aus dieser Gruppe
mit folgenden Eigenschaften vor:
T: → i+1;
U - beliebig aus Zweierzyklen bestehend;
V - beliebig aus Einer- und Zweierzyklen bestehend;
X, Y, Z - beliebig.
Unter Benutzung dieser Permutationen erfolgt die Umformung
von K in eine gleichlange Folge C:
C = {c1, c2, …, cj, …, cm};
cj ∈ R(26) für alle j = 1, 2, …, m; auf die folgende Weise:
1) Die Umformung von kj in cj (j = 1, 2, …, m) erfolgt mit Hilfe
einer Permutation S ∈ Sy(26), S: qi → pi. Dabei ist kj eines
der qi und cj das entsprechende pi. S hat die Gestalt
S = VTxXTy-xYTz-yZT-zUTzZ-1Ty-zY-1Tx-yX-1T-xV-1.
Dabei ist x, y, z ∈ R(26).
2) Die Umformung beginnt mit k1, wobei x = x1, y = y1, z = z1
vorgegeben sind. Ist kj mittels x, y, z umgeformt, dann wird kj+1
(j = 1, 2, …, m-1) mittels x', y', z' umgeformt, wobei folgende
Beziehungen bestehen; y und x sind vorgegeben:
x ≠ x, y ≠ y,: x' = x + 1, y' = y, z' = z + 1;
x = x, y ≠ y,: x' = x + 1, y' = y + 1, z' = z;
y = y: x' = x + 1, y' = y + 1, z' = z + 1;
Damit ist der Algorithmus vollständig beschrieben.
4. Nachweis, daß ENIGMA den Algorithmus realisiert, und dessen
kryptologische Deutung
Wir zeigen nun, daß die Variante von ENIGMA mit Steckerverbindung
und drei Walzen den beschriebenen Algorithmus realisiert.
R(26) entspricht dem Grundbereich, seine Elemente (Grundeinheiten)
sind die 26 Buchstaben A, B, C, …, Y, Z. Grundbereich und Ge-
heimbereich fallen zusammen.
K entspricht dem Grundtext und C dem Geheimtext.
X, Y, Z entsprechenden drei beweglichen Walzen, U der Umkehr-
walze und V der Steckerverbindung.
Eine ausführliche Herleitung der Formel für S findet man be-
reits in (1). S ist kryptologisch eine Substitution. Der Algo-
rithmus beschreibt ein Substitutionsverfahren (kein Additions-
verfahren !) und zwar ein Spaltenverfahren, da verschiedene S
auftreten können.
Die Beschreibung des Schrittschaltwerks in (1) ist unkorrekt bzw.
unvollständig, wir geben eine umfassende Darstellung.
Jeder Tastendruck löst eine Bewegung des Walzensatzes aus, die
im einzelnen wie folgt abläuft: Alle Walzen drehen in gleicher
Richtung jeweils max. einen Schritt. In der Regel wird lediglich
die rechte Walze um einen Schritt weiterbewegt. Die Fortschaltung
ist jedoch von der eines allgemein üblichen Zählers verschieden.
Jede Walze besitzt eine ausgezeichnete Stellung. Wird diese
nach einer bestimmten Anzahl Drehungen (Schritten) erreicht
oder war sie mit dem Anfangswert vorgegeben, so wird im näch-
sten Schritt gleichzeitig mit dieser Walze auch die links (be-
trifft die rechte und mittlere Walze) und rechts (betrifft
mittlere Walze) von ihr befindliche Walze weiterbewegt. (Bei
einem Zählwerk mit drei Zählrädern wird die linke Walze nur
bewegt, wenn die mittlere und die rechte Walze die
ausgezeichnete Stellung - beim Zählen die Ziffer 9 - erreicht
haben).
Dieser Sachverhalt widerspiegelt sich im Algorithmus, wenn
man Z als linke, Y, als die mittlere und X als die rechte Wal-
ze ansieht; x ist die ausgezeichnete Stellung von X und y die
ausgezeichnete Stellung von Y. Die Umkehrwalze befindet sich
links vom Walzensatz.
x1, y1, z1 entsprechen der Anfangseinstellung der Walzen (An-
fangswert), die im allgemeinen den Spruchschlüssel darstellt.
5. Elementare Eigenschaften des Algorithmus und ihre krypto-
logische Deutung
5.1 Eigenschaften der Permutation S
S ist zu U konjugiert. Somit besteht S ebenfalls nur aus Zwei-
erzyklen, da bei der Konjugiertenbildung Anzahl und Längen der
Zyklen invariant bleiben. Es gilt S2 = E (identische Permutation),
S-1 = S.
S stellt kryptologisch eine reziproke Substitution dar. Die
Chiffrierung erfolgt genauso wie die Dechiffrierung (ohne Um-
schalten).
Es ist immer kj ≠ cj (Ansatzpunkt für Dekryptierversuche).
Die bei beliebigen U, V, X … maximal mögliche Anzahl
von Substitutionen S beträgt

(Anzahl aller zweizyklischen Permutationen 26. Ordnung).
Für beliebige ganze Zahlen s und t ist Ts+26t = Ts. Also be-
sitzt T nur 26 verschiedene Potenzen. Daraus folgt, daß bei
festen U, V, X, Y, Z höchstens 263 = 17576 verschiedene
Substitutionen möglich sind.
5.2 Permutationsfolgen
Für analytische Untersuchungen erscheint es zweckmäßig, meh-
rere verschiedene Folgen zu betrachten. Wir nehmen an, daß
U, V, X, Y, Z, x, y fixiert seien.
(NF) die "natürliche Folge"
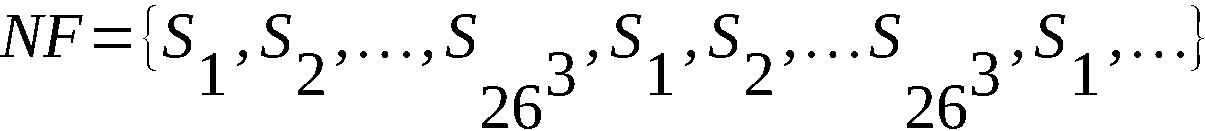
ist unendlich mit der Periode 263. Hier ist für i = 1, 2, …, 263
Si = S(x, y, z), i = x + (y-1)·25 + (z-1)·262
also z. B. S1 = S(1, 1, 1), S2 = S(1, 1, 1), S27 = S(1, 2, 1).
NF enthält alle Permutationen, die bei irgendeinem Anfangswert
auftreten können, in einer vom mathematischen Standpunkt na-
türlichen Reihenfolge, die Gesetzmäßigkeiten vielleicht am
ehesten erkennen läßt. Die Zuordnung i ←→ (x, y, z) ist ein-
eindeutig.
(SF) Mit S(j) bezeichnen wir die Permutation S, die kj in cj
überführt (j = 1, 2, …, m), und mit SF die vom Al-
gorithmus abgearbeitete Folge
SF = {S(1), S(2), …, S(j), …, S(m)}.
SF ist kryptologisch die Substitutionsreihe zur Chiffrierung
des Grundtextes K, z. B. ist S(1) = S(x1, y1, z1). SF ist im
Gegensatz zu NF verschieden für verschiedene Anfangswerte
x1, y1, z1. Entsprechend den verschiedenen Möglichkeiten für
die Anfangswerte sind bei beliebigem, aber festem m 263
verschiedene SF möglich.
Zwei verschiedene SF sind bei hinreichender Länge stets phasen-
gleich.
Wie sich aus dem Algorithmus erkennen läßt, treten nicht alle
für NF definierten Si (i = 1, 2, …, 263) in jeder hin-
reichend langen Folge SF auf. Einige können nur S(1) oder S(2)
sein. Letztere wollen wir als singuläre Permutationen bezeich-
nen, erstere als reguläre. Es gibt 262 singuläre Permutationen
und entsprechend 25·262 reguläre. Die singulären Permutationen
sind
S(x + 1, y + 1, z), S(x ≠ x + 1 , y, z).
Es ergibt sich, daß SF bei hinreichend großem m eine Periode
der Länge 25·262 besitzt, die entweder mit S(1) oder mit S(2)
oder mit S(3) beginnt. SF besteht, ev. mit Ausnahme von S(1)
bzw. S(1) und S(2), aus regulären Permutationen.
(VF) Die "vollständige" Folge VF wird gebildet, indem irgend-
ein SF mit allen singulären Permutationen aufgefüllt und ins
Unendliche fortgesetzt wird. Die singulären Permutationen
werden so eingefügt, daß, wären sie S(1), die nächstfolgende
Permutation S(2) wäre. (Explizite Darstellung von VF siehe
Blatt 7, daraus ist u. a. die Verteilung der singulären Subs-
titution in VF ersichtlich).
VF hat eine Periode der Länge 263. Alle Permutationsfolgen
SF mit beliebigen Anfangswerten und beliebiger Länge sind
endliche, nicht zusammenhängende (bei hinreichender Länge)
Teilfolge der unendlichen periodischen Permutationsfolge VF.
Kryptologisch bedeutet das, daß alle Substitutionsreihen SF
phasenähnlich VF sind.
5.3 Gleiche Permutationen
Die kryptologische Sicherheit ist, abgesehen von anderen
Faktoren, um so höher, je mehr voneinander verschiedene
Substitutionen in VF auftreten. Wann ist
S(x', y', z') = S(x'', y'', z''),
wenn nicht gleichzeitig x'=x'', y'=y'', z'=z'' ?
Eine hinreichende Bedingung für Gleichheit ist die Erfüllung
folgender Gleichungen durch X, Y, Z:
Tx'X = XTx' Ty'Y = YTy' Tz'Z = ZTz'
Tx''X = XTx'' Ty''Y = YTy'' Tz''Z = ZTz''
Hieraus folgt, daß es zweckmäßig ist, die Permutationen in
den Walzen so zu wählen, daß sie für kein k Lösungen der
Gleichung TkP = PTk sein können.
Es ist denkbar, daß auch in anderen Fällen gleiche Substitu-
tionen auftreten können.
5.4 Darstellung der Folge VF
… (x + 2 y z + 1)
(x y z ) x + 3 y + 1 z + 2
(x + 1 y + 1 z + 1) …
x + 2 y + 1 z + 1 x + 25 y + 1 z + 2
(x + 2 y z ) (x + 25 y z + 1)
x + 3 y + 1 z + 1 x y + 1 z + 2
(x + 3 y z ) x + 1 y + 2 z + 2
x + 4 y + 1 z + 1 …
… x y + 2 z + 2
x + 25 y + 1 z + 1 …
(x + 25 y z ) x + 1 y + 25 z + 2
x y + 1 z + 1 …
x + 1 y + 2 z + 1 x y + 25 z + 2
x + 2 y + 2 z + 1 x + 1 y z + 2
… (x y z + 2)
x + 25 y + 2 z + 1 (x + 1 y + 1 z + 3)
x y + 2 z + 1 x + 2 y + 1 z + 3
x + 1 y + 3 z + 1 …
… x y + 25 z
x y + 3 z + 1 x + 1 y + 25 z
… (x y z )
x + 1 y + 25 z + 1 (x + 1 y + 1 z + 1)
… x + 2 y + 1 z + 1
x y + 25 z + 1 …
x + 1 y z + 1
(x y z + 1)
(x + 1 y + 1 z + 2)
x + 2 y + 1 z + 2
Die singulären Permutationen sind in Klammern gesetzt.
6. Aufgaben für weitere Untersuchungen
6.1 Gruppeneigenschaften der Permutationen: Bilden die S
eine Gruppe?
Wenn nicht, wie sieht die kleinste sie enthaltende
Gruppe aus?
Usw.
6.2 Sammlung aller Eigenschaften konjugierter Permutationen
und konjugierter Elemente in Gruppen.
6.3 Untersuchung der Gleichung in Permutationen TkP = PTk.
6.4 Beziehungen innerhalb der Folgen NF, SF, VF:
Beziehungen zwischen aufeinanderfolgenden Permutationen.
Anzahl der tatsächlich verschiedenen Permutationen. Häufig-
keitsverteilung in den Folgen. Existenz von Unterperioden.
Parallelstellen.
Beziehungen zwischen NF und VF.
6.5 Beziehungen zwischen NF und zwischen VF bei Vertauschung
der Reihenfolge der Walzen.
6.6 Dekryptiermethoden.
6.7 Ist die vereinfachende Voraussetzung x = y = 16 zulässig?
6.8 Effektiver Schlüsselvorrat, äquivalente und ähnliche Schlüssel.
Krey
Oltn.
E N I G M A
=============
Kurzgefaßte Darstellung
der Auflösungsmethoden.
Inhaltsverzeichnis
1. Einleitung
2. Die Anfänge
3. Zyklentheorie
4. Zwei wichtige Schriftstücke
5. Substitutionentheorie
6. Substitution E
7. Die Substitution S
8. Einige Ziffern
9. Auffindung der Spruchschlüssel
10. Methode der charakteristischen Schlüssel
11. Die statistische Methode
12. Methode ungleicher Buchstaben
13. Bestimmung der rechten Walze
14. Der Rost
15. Der Katalog F
16. Der Zyklometer
17. Grundstellung und Ringstellung
18. Einige Bemerkungen
19. Neue Netze. Beständige Änderungen
20. Umkehrwalze B
21. Neue Chiffrierwalzen
22. Änderung des Chiffriersystems
23. Auffindung der Walzenlage
24. Bomben
25. Die Netze
26. Die Warschauer Konferenz
27. Kriegsaufbruch. Vignolles
28. Methode Knox
29. Kataloge zu den Netzen
30. Methode Herivel
31. Drittes Schlüsselverfahren
32. Chronologische Übersicht über die Änderungen des
Schlüsselverfahrens im Heer und in der Luftwaffe
33. Das Funknetz des Sicherheitsdienstes
34. Die Schlüsselverfahren der deutschen Kriegsmarine
vor Einführung der Enigma
35. Die Marine-Chiffriermaschine mit 29 Tasten
36. Die Anwendung in der deutschen Kriegsmarine der
Enigma-Chiffriermaschine mit 26 Tasten
37. Chronologische Übersicht über die Anwendung von
Enigma-Chiffriermaschinen in der deutschen Kriegsmarine
38. Teilnahme der drei Staaten an der Lösung der Enigma
1. Einleitung
Bereits wenige Jahre nach Beendigung des Weltkrieges begann // Erster Weltkrieg
die deutsche Wehrmacht zur Verschlüsselung von Nachrichten,
die auf dem Funkwege übersandt werden sollten, sich der
"Enigma-Chiffriermaschine" zu bedienen.
Als erste führte, wie es scheint, die deutsche Kriegsmarine
dieses Schlüsselverfahren bei sich ein. Jedenfalls ist gewiß,
daß sie es bereits im Jahre 1926 benutzte, während seine An-
wendung im deutschen Heer erst ab 15. Juli 1928 festgestellt
wurde.
Am 1. August 1935 folgte dann mit der Einführung der Enigma
die deutsche Luftflotte, vom September 1937 ab bediente sich
ihrer der Sicherheitsdienst, auch von der Polizei wurde sie
benutzt. Während sich so der Gebrauch der Enigma in der deu-
tschen Wehrmacht immer mehr verbreitete, begannen andere
Schlüsselmethoden, wie z.B. Doppelwürfelverfahren, allmählich
zu verschwinden, so daß bereits eine gewisse Zeit vor Beginn
des Deutsch-Polnischen Krieges 1939 beinahe alles, was von der
deutschen Institutionen militärischen oder halbmilitärischen
Charakters dem Funkwege anvertraut wurde, mit der Enigma-
Maschine verschlüsselt war. Die Lösung dieses Schlüsselverfah-
rens bildete daher für die Generalstäbe Polens, Frankreichs
und Großbritannien ein Problem von erstklassiger Bedeutung.
Im Laufe der Jahre wurde der Typ der Maschine mehrfach geändert.
Vor Einführung der Enigma "M" mit Steckerverbindung, die noch
heute im Gebrauch ist, benutzte das deutsche Heer in der Zeit
vom 15. Juli bis 31. Mai 1930 die Enigma "G" mit Stöpselstellung. // Fernmeldeklinken-Stecker
Bei den Wehrkreiskommandos bediente man sich eine Zeit lang
einer selbstschreibenden Maschine, der sogenannten "Enigma II",
die jedoch anscheinend als unpraktisch bald aus dem Verkehr
gezogen wurde. Die deutsche Kriegsmarine wiederum wandte bis
September 1934 einen Maschinentyp mit 29 statt mit 26 Tasten
an und ging erst ab Oktober 1934 zum Gebrauch derselben Maschine
wie die deutsche Heer über. Übrigens bewahrte die deutsche Kriegs-
marine auch späterhin eine gewisse Selbstständigkeit, indem sie
in gewissen Zeiträumen eine größere Anzahl von Schlüsselwalzen
benutzte als die übrigen Formationen. Grundsätzlich kann man
jedoch sagen, das ab Oktober 1934 bis heute nur ein Maschinen-
typ gebraucht wird, derselbe, dessen sich das deutsche Heer
seit 1. Juli 1930 bedient.
Im folgendem wird skizziert, auf welche Weise dem Schlüssel-
dienst des polnischen Generalstabes gelang, den oben angeführ-
ten Typ der Enigma wiederherzustellen und welche Verfahren
weiterhin ausgedacht wurden, um das eingehende Chiffriermate-
rial fast stets laufend zu lösen, trotz sämtlicher Verände-
rungen und Verbesserungen, die andauernd vom deutschen Schlüs-
seldienst eingeführt wurden, um das Verfahren absolut unlösbar
zu machen. Es wird auch dargestellt werden, von wie großer
Trägheit die Zusammenarbeit der Generalstäbe Polens, Frank-
reichs und Großbritannien sich in dieser Hinsicht erwies.
2. Die Anfänge
Noch mehrere Jahre nach Gründung des polnischen Schlüssel-
dienstes konnte aus Personalmangel dem einlaufenden Schlüssel- // chiffrierte Texte
material der deutschen Kriegsmarine keine Beachtung geschenkt
werden. Daher wurde das Erscheinen der Enigma erst in dem Au-
genblick bemerkt, als sich ihrer das deutsche Heer zu bedienen
begann, d.h. im Jahre 1928.
Unter den einlaufenden Sprüchen, die von deutschen Militärfunk-
stationen aufgegeben wurden, zeigten sich damals neben solchen,
die wie bisher nach dem Doppelwürfelverfahren geschlüsselt
waren, auch andere, die zweifellos den Charakter eines Substi-
tutionverfahrens aufwiesen. Man begann sich mit ihnen zu be-
schäftigen und stellte leicht fest, daß die sechs ersten Buch-
staben eines jeden Spruches eine besondere Bedeutung hatten
und wahrscheinlich den Schlüssel des gegebenen Spruches dar-
stellten. Gleichzeitig gelang es dem polnischen Nachrichten-
dienst, in dem Besitz mehrerer kleiner Schriftstücke zu
kommen, aus denen hervorging, daß vom 15. Juli 1928 ab im
deutschen Heer neben den bisherigen Schlüsselverfahren als
neues das "Maschinenschlüsselverfahren Enigma G" in Kraft
trat, daß bei der Enigma eine Stöpselstellung (während bei
dem späteren Typ eine Steckerverbindung) vorhanden war, und
daß jede Dienststelle in gewissen Zeitabständen eine Anzahl
von Schlüsseln zugeteilt bekommt, von denen aus drei Zahlen
nicht größer als 26 besteht.
Es war nunmehr klar, daß das neue Schlüsselverfahren, das man
entdeckt hatte, identisch mit dem Enigmaschlüsselverfahren war.
Um das Studium dieses Verfahrens zu erleichtern, wurde vom
polnischen Generalstab eine Enigma vom Handelstypus angekauft,
bei der selbstverständlich die Walzen ganz andere Schaltungen
hatten, als bei der Dienste des Heeres stehende Maschine, die
sich aber auch sonst noch, wie sich später herausstellte, in
mehrerer Hinsicht stark von der letzteren unterschied.
Die Untersuchungen dieses Schlüsselverfahrens wollten jedoch
nicht recht von der Stelle rücken und wurden nach einiger
Zeit abgebrochen.
3. Zyklentheorie // = Kettenkomplex
Die Wiederaufnahme der Arbeiten erfolgte im Jahre 1932. Man
unterzog die ersten 6 Buchstaben der Sprüche einer erneuten
Untersuchung und stellte dabei folgendes fest: Für jeden Tag
wird eine gewisse Stellung der Walzen, eine und dieselbe für
sämtliche Schlüssler, festgesetzt. Daraufhin wählt sich jeder // Schlüssler = Chiffreur
Schlüssler drei beliebige Buchstaben, schlüsselt sie zweimal
hintereinander ausgehend von der für diesen Tag festgesetzten
Stellung der Walzen und setzt die so erhaltenen 6 Buchstaben
in den Anfang des Spruches ein.
Auf diese Weise entstehen zwischen dem 1. und 4., bzw. 2. und
5., bzw. 3. und 6. Buchstaben der Sprüche gewisse Beziehungen,
die eine rein mathematische Behandlungsweise gestatteten und
die Grundlage der späteren Wiederherstellung der Enigma bil-
deten.
Man verfährt folgendermaßen: Man nimmt irgendeinen Spruch,
schreibt dessen ersten Buchstaben und rechts davon vierten
Buchstaben auf. Dann sucht man einen Spruch, in dem der zu-
letzt aufgeschriebene Buchstabe als erster Buchstabe auftritt
und schreibt recht vom dessen vierten Buchstabe auf. So ver-
fährt man weiter, bis man zum ersten Buchstabe zurückkehrt.
Das erhaltene Ergebnis nennt man einen Zyklus. Man kann fol-
gende Sätze beweisen:
1) Zyklen derselben Länge treten stets in gerader Zahl auf.
2) Buchstaben eines Zyklus werden durch Buchstaben hervorge-
rufen, die in einem anderen, gleichlangen Zyklus auftreten.
3) Wird eine Buchstabe X durch einen Buchstaben Y hervorgeru-
fen, so wird der rechts von X stehende Buchstabe durch den
links von Y stehenden Buchstabe hervorgerufen.
Diese drei Sätze lösten teilweise die Aufgabe, die Spruch-
schlüssel zu rekonstruieren, und bestimmt hätte man schon
damals dieses Problem vollständig gelöst, wenn nicht gerade
in diesem Augenblick Hilfsmittel zur Verfügung gestellt worden
wären, die Arbeiten in andere Bahnen lenkten.
4. Zwei wichtige Schriftstücke
In dieser Zeit gelangte nämlich die polnische Schlüsselstelle // Chiffrierbüro
in den Besitz zweier Schriftstücke von außerordentlicher Be-
deutung. Das erste dieser beiden Schriftstücke trug die Über-
schrift: "Anleitung zum Maschinenschlüsselverfahren", während
das andere die sogenannten Tagesschlüssel zur Enigma für die
Monate Oktober und Dezember 1931 enthielt. Diese Schriftstücke
erhielt die polnische Schlüsselstelle vom französischen Ge-
neralstab, der in ihren Besitz durch seinen Nachrichtendienst
gelang war. Es muß betont werden, daß der Besitz dieser
Schriftstücke und zwar besonders der Tagesschlüssel entschei-
dend den Fortgang der Arbeiten beeinflußt hat. Ohne diese
Dokumente wäre die Lösung des Enigmaschlüsselverfahrens zu-
mindest um Jahre verzögert worden. Andererseits mag jedoch
auch festgestellt werden, daß es weder der französischen noch
der englischen Schlüsselstelle gelungen war, das Verfahren zu
lösen, trotzdem beide Stellen im Besitz dieser Schriftstücke
waren. Übrigens wird weiter unten eine Methode angegeben wer-
den, die eventuell auch ohne den genannten Schriftstücken zum
Ziele geführt haben würde.
Aus dem ersten der genannten Dokument ging hervor, daß ab
1. Juni 1930 an Stelle der bisherigen Enigma mit Stöpselstel-
lung eine neue Enigma mit Steckerverbindung trat. Weiter er-
fuhr man noch folgendes:
1) Die Maschine enthält 3 Schlüsselwalzen, deren Lage ver-
ändert werden kann. Änderung der Walzenlage erfolgt alle
drei Monate.
2) Die Umkehrwalze ist fest (im Gegensatz zur Enigma-Handels-
maschine).
3) Die Schlüsselwalzen sind mit einem Zahlen-, bzw. Buchstaben-
ring versehen. Änderung der Ringstellung erfolgt täglich.
4) Die Steckerverbindung vertauscht 6 Paar Buchstaben. Änderung
der Steckerverbindung erfolgt täglich.
5) Die Stellung, von der aus der Spruchschlüssel geschlüsselt
wird, heißt Grundstellung. Änderung der Grundstellung er-
folgt täglich.
Das zweite Dokument enthielt, wie bereits bemerkt wurde, die
Tagesschlüssel, d.h. Walzenlage, Grundstellung, Ringstellung,
Steckerverbindung, für die Dauer von zwei Monaten.
5. Substitutionentheorie
Man schritt nun zur Bewältigung des Hauptproblems, d.h. zur
Rekonstruktion der Walzenschaltungen. Man bediente sich hier-
bei einer mathematischen Theorie, der so genannten Substitution-
entheorie, die selbstverständlich hier nicht auseinandergesetzt
werden kann, sondern vielmehr als bekannt vorausgesetzt wird.
Man muß sich aber natürlich nicht vorstellen, daß es einfach
genügte, bekannte Sätze der Substitutionentheorie anzuwenden,
um das Ergebnis zu erhalten. Im Gegenteil war auf dem Wege zum
Endziele eine ganze Reihe überaus schwieriger Hindernisse zu
überwinden. Im Folgenden geben wir kurz den eingeschlagenen
Gedankengang an. Das Schlüsselverfahren Enigma ist ein Substi-
tutionsverfahren, d.h. die Maschine setzt in jeder Position
der Walzen für die Buchstabe des Alphabets andere Buchstaben
ein. Wir bezeichnen mit A1 die Substitution, der die Buchsta-
ben des Alphabets unterworfen sind, wenn sich die Walzen in
der für gegebenen Tag festgesetzten Grundstellung befinden,
mit A2 die Substitution in der nächstfolgenden Stellung der
Walzen u.s.w. bis A6.
Wenn man über genügende Anzahl von Sprüchen verfügt (im Durch-
schnitt etwa 80), so wird man mit Hilfe der Zyklentheorie zu-
nächst die Produkte A1A4, A2A5, A3A6 bilden können, die daher
als bekannt vorausgesetzt werden können. Wir bezeichnen nun
weiter durch
| S | die Substitution hervorgerufen durch die: | Steckerverbindungen |
|---|
| Cα | | rechte Schlüsselwalze |
| Cβ | | mittlere Schlüsselwalze |
| Cγ | | linke Schlüsselwalze |
| U | | Umkehrwalze |
| E | | Eintrittswalze |
| Q = (1, 2, 3, 4, 5, 6, . . . ., 24, 25, 26) |
Wenn während des Chiffrierens des Spruchschlüssels die mit-
tlere Walze sich nicht fortbewegt, was ziemlich wahrscheinlich
ist, und was wir im Folgenden voraussetzen wollen, so können
die Substitutionen A1 bis A6 auf folgende Weise dargestellt
werden:
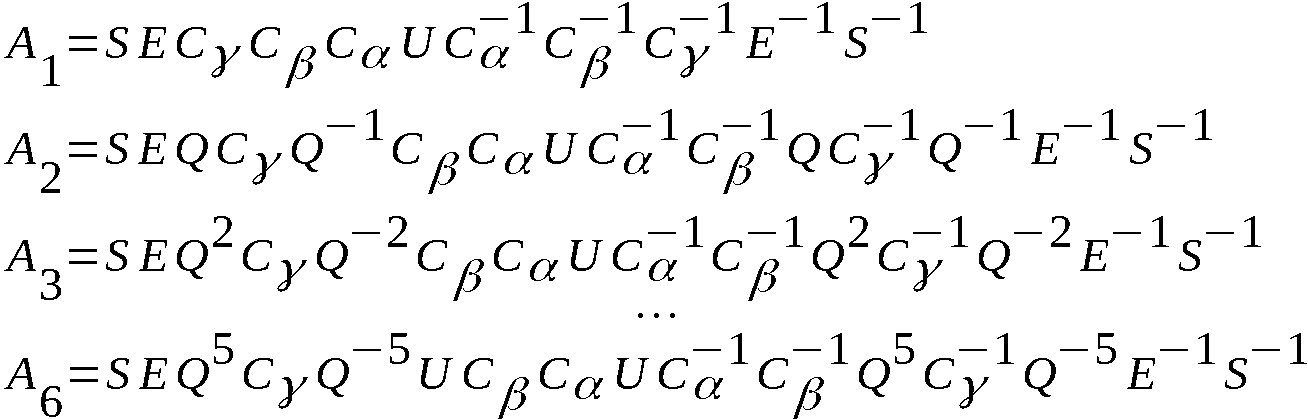
Die erste Schwierigkeit, die zu überwinden war, bestand darin,
daß nicht nur die rechten, sondern auch die linken Seiten der
Gleichungen unbekannt sind, bekannt sind nur die Produkte A1A4,
A2A5, A3A6. Die Zyklentheorie lehrt uns jedoch, daß die Substi-
tution A1 in den meisten Fällen nicht mehr als etwa hundert
Bezeichnungen annehmen kann und daß gleichzeitig jede Bezeich-
nung von A1 eindeutig die Substitution A4 festsetzt. Dasselbe
gilt von A2 und A5, bzw. A3 und A6. Man kann sich also vor-
stellen, daß sämtliche Bezeichnungen von A1 bis A6 aufgeschrie-
ben sind. Auf diese Weise kann man die erste Schwierigkeit
als überwunden betrachten, auf Kosten allerdings einer viel-
fachen Vergrößerung der Arbeitszeit, denn bei den weiteren
Operationen müssen sämtliche möglichen Bezeichnungen für A1
bis A6 der Reihe nach eingesetzt werden.
Die zweite Schwierigkeit ist noch viel ernster. Trotz größter
Bemühungen nämlich, die noch jahrelang aus theoretischen Grü-
nden fortgesetzt wurden, nachdem die Walzenschaltungen schon
längst gefunden waren, ließen sich die oben angeführten Gleich-
ungen auf keine Weise lösen, das größte Hindernis stellte stets
die Substitution S, d.h. die Steckerverbindung dar. Man hat
schließlich eine Methode gefunden, die vielleicht zum Ziele
geführt hätte, sie setzte jedoch die Kenntnis der Substitutionen
A1 bis A6 (und nicht Bloß der Produkte A1A4, A2A5, A3A6), die
Kenntnis der Substitution E, und ferner recht umfangreiches
Material voraus.
So wurde denn die zweite und Hauptschwierigkeit auf dem Wege
der Lösung der Enigma vor allem durch das vom französischen
Generalstab zur Verfügung gestellte Schriftstück, das die
Steckerverbindungen für zwei Monate enthielt, überwunden.
Die dritte Schwierigkeit beruhte auf der Unkenntnis der Sub-
stitution E. Es scheint, daß dies das Hindernis war, am dem
die Bemühungen der englischen Kryptologen gescheitert sind.
Spätere Untersuchungen in der polnischen Schlüsselstelle er-
gaben, daß man die Substitution E auf dem deduktiven Wege
hätte finden können (vorausgesetzt, daß S bekannt ist), in
Wirklichkeit jedoch fand man E durch Probieren. Man nahm zu-
nächst an, die Substitution E sei dieselbe wie in der Enigma-
Maschine vom Handelstypus, d.h.:

Als man mit dieser Annahme kein Resultat erzielte, glaubte
man anfangs, das am gewählten Tage während der Chiffrierung
des Tagesschlüssel eine Verschiebung der mittleren Walze statt-
fände. Man wiederholte also die ganzen Operationen noch einmal
auf dem Material eines anderen Tages und, als man wieder kein
Ergebnis erzielte, nahm man einen dritten und vierten und
fünften Tag.
Die Arbeiten, die bereits Monate dauerten, sollten schon ab-
gebrochen werden, als man noch einen Versuch machte und zwar
unter der Annahme

Diesmal hatte man Glück, die Annahme stellte sich als richtig
heraus und führte zur Lösung der Aufgabe.
Zur Orientierung des Lesers wird mitgeteilt, daß zur Auffindung
der Schaltungen der rechten Walze unser oben angeführtes System
von 6 Gleichungen zunächst auf folgende Form gebracht werden muß.

Die Gleichungen sind trotz ihrer Länge nicht besonders kom-
pliziert. Alle Ausdrücke auf der linken Seite sind bekannt,
alle Ausdrücke auf der rechten Seite haben einen gemeinsamen
Mittelteil. Durch Elimination dieses Teiles erhält man 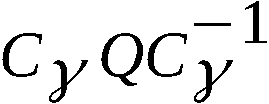 und hierdurch unmittelbar Cγ, d.h. die Schaltungen der
rechten Walze.
Man mußte selbstverständlich noch die Schaltungen der linken,
mittleren und Umkehrwalze auffinden sowie die Positionen, bei
denen die Walzen sich drehten, da man jedoch hierbei keine
grundsätzlich neuen Methoden anwandte, so mögen die diesbe-
züglichen Arbeiten übergangen werden.
6. Substitution E
Wir wollen kurz skizzieren, wie man die Substitution E auch
deduktiv hätte finden können.
Da wir im Besitz der Tagesschlüssel für zwei Monate sind, können
wir leicht zwei solche Tage finden, in denen sowohl die Walzen-
lage als auch Position der rechten Walzen, d.h. die Differenz
zwischen Grund- und Ringstellung der rechten Walze dieselbe ist.
Wir stellen für diese beiden Tage die zwei Gleichungssysteme
A1 bis A6 auf, und erhalten, wenn wir zur Abkürzung
und hierdurch unmittelbar Cγ, d.h. die Schaltungen der
rechten Walze.
Man mußte selbstverständlich noch die Schaltungen der linken,
mittleren und Umkehrwalze auffinden sowie die Positionen, bei
denen die Walzen sich drehten, da man jedoch hierbei keine
grundsätzlich neuen Methoden anwandte, so mögen die diesbe-
züglichen Arbeiten übergangen werden.
6. Substitution E
Wir wollen kurz skizzieren, wie man die Substitution E auch
deduktiv hätte finden können.
Da wir im Besitz der Tagesschlüssel für zwei Monate sind, können
wir leicht zwei solche Tage finden, in denen sowohl die Walzen-
lage als auch Position der rechten Walzen, d.h. die Differenz
zwischen Grund- und Ringstellung der rechten Walze dieselbe ist.
Wir stellen für diese beiden Tage die zwei Gleichungssysteme
A1 bis A6 auf, und erhalten, wenn wir zur Abkürzung
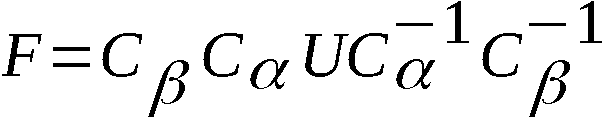
setzen und die Buchstaben, die sich auf zweiten Tag beziehen,
unterstreichen:

Hieraus bilden wir folgende Gleichungen, in denen die rechten
Seiten bekannt sind:
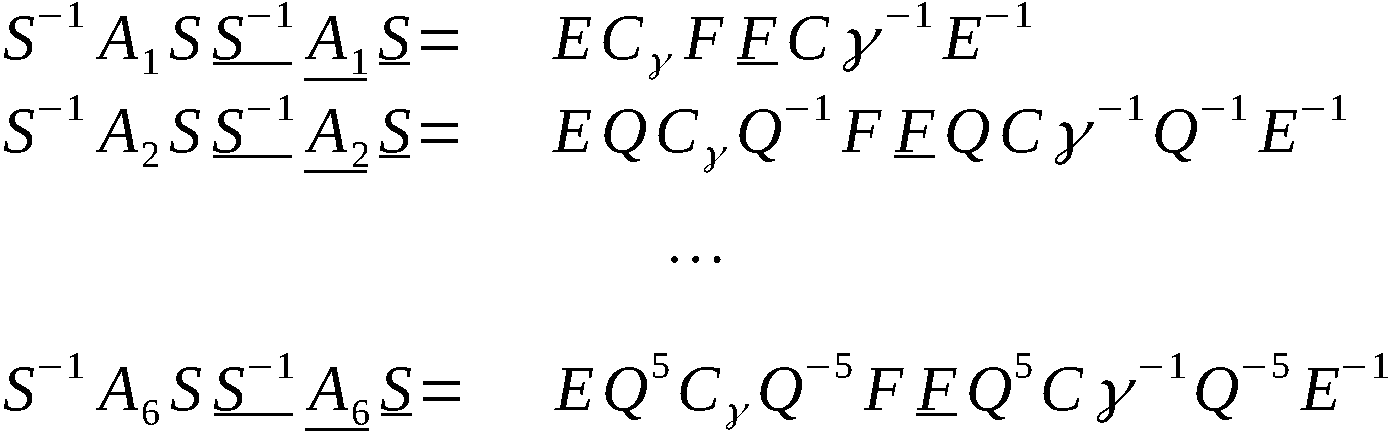
Durch Elimination von F F erhalten wir die Ausdrücke:

Und hieraus durch Elimination von  zunächst
zunächst  ,
und hieraus unmittelbar E.
Der Weg zum Ergebnis ist recht lang, besonders wenn die Substi-
tutionen A1 bis A6 selbst nicht, sondern nur die Produkte A1A4,
A2A5, A3A6 bekannt sind, und die tatsächliche Ausführung der
hier skizzierten Operationen wurde eine Person sicherlich
mehrere Monate lang in Anspruch nehmen. Jedenfalls aber möge
festgestellt werden, daß, wenn nur die Steckerverbindungen
bekannt sind, man stets auf diese oder andere Weise zum Ziel
gelangt wäre.
7. Die Substitution S
Wir wollen endlich noch einen Weg zeigen, wie man wahrschein-
lich auch zum Ziele gelangt wäre, wenn man nicht im Besitze
der Schlüssel für zwei Monate befunden hätte. Es muß hierbei
allerdings vorausgesetzt werden, daß die Substitution E bekannt
ist oder wenigstens erraten wie es in Wirklichkeit geschehen
ist. Ferner muß angenommen werden, daß die Substitutionen
A1 bis A6 selbst und nicht Bloß die Produkte A1A4, A2A5, A3A6
bekannt sind. Auch das hätte man sicherlich erzielt. Und end-
lich müssen wir über so umfangreiches Material verfügen, daß
wir in mehreren hundert Tagen die Substitutionen A1 bis A6
bilden können. Wenn alle diese Voraussetzungen erfüllt sind
so ist es zu erwarten, daß man zwei Tage findet, in denen die
Walzenlage dieselbe ist, die Differenz zwischen Grund- und
Ringstellung der linken und mittleren Walze dieselbe ist, und
die Differenz zwischen Grund- und Ringstellung der rechten
Walze sich um nicht mehr als 3 unterscheidet. Tritt ein sol-
cher Fall ein, so ist er leicht aufzudecken. Denn nehmen wir
etwa an, die Positionen der rechten Walzen unterscheiden sich
in den beiden Tagen um 3, so daß etwa die Substitutionen A1
und A4 in derselben Position entstehen. Dann müssen zunächst
einmal die Produkte A1A2 und A4A5 einerseits und die Produkte
A2A3 und A5A6 anderseits ähnlich sein, wie man leicht überzeugt,
wenn man die betreffenden Gleichungen aufschreibt:
,
und hieraus unmittelbar E.
Der Weg zum Ergebnis ist recht lang, besonders wenn die Substi-
tutionen A1 bis A6 selbst nicht, sondern nur die Produkte A1A4,
A2A5, A3A6 bekannt sind, und die tatsächliche Ausführung der
hier skizzierten Operationen wurde eine Person sicherlich
mehrere Monate lang in Anspruch nehmen. Jedenfalls aber möge
festgestellt werden, daß, wenn nur die Steckerverbindungen
bekannt sind, man stets auf diese oder andere Weise zum Ziel
gelangt wäre.
7. Die Substitution S
Wir wollen endlich noch einen Weg zeigen, wie man wahrschein-
lich auch zum Ziele gelangt wäre, wenn man nicht im Besitze
der Schlüssel für zwei Monate befunden hätte. Es muß hierbei
allerdings vorausgesetzt werden, daß die Substitution E bekannt
ist oder wenigstens erraten wie es in Wirklichkeit geschehen
ist. Ferner muß angenommen werden, daß die Substitutionen
A1 bis A6 selbst und nicht Bloß die Produkte A1A4, A2A5, A3A6
bekannt sind. Auch das hätte man sicherlich erzielt. Und end-
lich müssen wir über so umfangreiches Material verfügen, daß
wir in mehreren hundert Tagen die Substitutionen A1 bis A6
bilden können. Wenn alle diese Voraussetzungen erfüllt sind
so ist es zu erwarten, daß man zwei Tage findet, in denen die
Walzenlage dieselbe ist, die Differenz zwischen Grund- und
Ringstellung der linken und mittleren Walze dieselbe ist, und
die Differenz zwischen Grund- und Ringstellung der rechten
Walze sich um nicht mehr als 3 unterscheidet. Tritt ein sol-
cher Fall ein, so ist er leicht aufzudecken. Denn nehmen wir
etwa an, die Positionen der rechten Walzen unterscheiden sich
in den beiden Tagen um 3, so daß etwa die Substitutionen A1
und A4 in derselben Position entstehen. Dann müssen zunächst
einmal die Produkte A1A2 und A4A5 einerseits und die Produkte
A2A3 und A5A6 anderseits ähnlich sein, wie man leicht überzeugt,
wenn man die betreffenden Gleichungen aufschreibt:
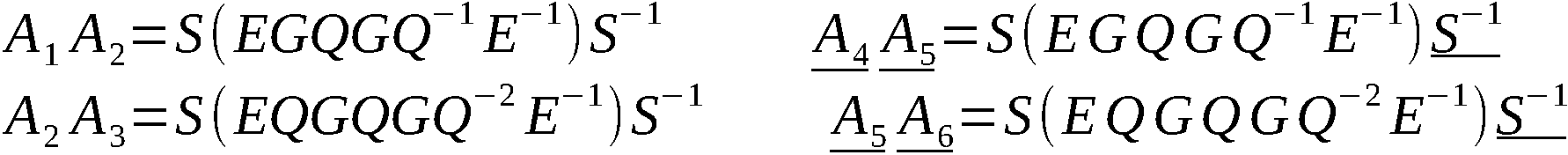
wobei man zur Abkürzung  gesetzt hat.
Ferner kann man aus den Gleichungen A1A2 und A4A5 und aus
den Gleichungen A2A3 und A5A6 andererseits das Produkt SS er-
rechnen und dies Produkt muß in beiden Fällen gleich sein.
Und schließlich muß das Produkt SS aus mindestens 14 Zyklen
bestehen.
Die Hauptschwierigkeit besteht nun darin, daß auf diese
Weise nur das Produkt SS und nicht die Substitutionen S und
S einzeln erhält. Es zeigt sich aber, daß im Allgemeinen S
und S nur mehrere hundert verschiedene Werte annehmen werden.
Wir müssen also diese Werte der Reihe nach in unseren Gleich-
ungen einsetzen und versuchen, zu einem Ergebnis zu gelangen.
Eine sehr große Arbeit, die sicherlich unausführbar wäre,
wenn auch noch die Substitutionen A1 bis A6 nicht einzeln,
sondern nur ihre Produkte zu Zweien bekannt wären.
8. Einige Ziffern
Eine vollständige Beschreibung der Maschine Enigma würde den
Rahmen dieser Skizze weit überschreiten. So wollen wir uns
denn begnügen einige Zahlen anzugeben, um zu zeigen, wie ein
starkes Instrument vom kryptologischen Standpunkt aus die
Enigma darstellt, vorausgesetzt natürlich, daß sie richtig
angewandt wird.
Die Anzahl verschiedener Walzenlagen beträgt bei den drei Walzen
3 · 2 · 1 = 6
und bei fünf Walzen
5 · 4 · 3 = 60
Die Zahl der verschiedenen Grundstellungen und Ringstellungen
beträgt je
263 = 17.576
Die Zahl verschiedener Positionen der Walzen beträgt mithin
(zusammen mit den Walzenlagen) bei drei Walzen
105.456
und bei fünf Walzen
1.054.560
Die Zahl verschiedener Steckerverbindungen beträgt bei 6
Paaren
gesetzt hat.
Ferner kann man aus den Gleichungen A1A2 und A4A5 und aus
den Gleichungen A2A3 und A5A6 andererseits das Produkt SS er-
rechnen und dies Produkt muß in beiden Fällen gleich sein.
Und schließlich muß das Produkt SS aus mindestens 14 Zyklen
bestehen.
Die Hauptschwierigkeit besteht nun darin, daß auf diese
Weise nur das Produkt SS und nicht die Substitutionen S und
S einzeln erhält. Es zeigt sich aber, daß im Allgemeinen S
und S nur mehrere hundert verschiedene Werte annehmen werden.
Wir müssen also diese Werte der Reihe nach in unseren Gleich-
ungen einsetzen und versuchen, zu einem Ergebnis zu gelangen.
Eine sehr große Arbeit, die sicherlich unausführbar wäre,
wenn auch noch die Substitutionen A1 bis A6 nicht einzeln,
sondern nur ihre Produkte zu Zweien bekannt wären.
8. Einige Ziffern
Eine vollständige Beschreibung der Maschine Enigma würde den
Rahmen dieser Skizze weit überschreiten. So wollen wir uns
denn begnügen einige Zahlen anzugeben, um zu zeigen, wie ein
starkes Instrument vom kryptologischen Standpunkt aus die
Enigma darstellt, vorausgesetzt natürlich, daß sie richtig
angewandt wird.
Die Anzahl verschiedener Walzenlagen beträgt bei den drei Walzen
3 · 2 · 1 = 6
und bei fünf Walzen
5 · 4 · 3 = 60
Die Zahl der verschiedenen Grundstellungen und Ringstellungen
beträgt je
263 = 17.576
Die Zahl verschiedener Positionen der Walzen beträgt mithin
(zusammen mit den Walzenlagen) bei drei Walzen
105.456
und bei fünf Walzen
1.054.560
Die Zahl verschiedener Steckerverbindungen beträgt bei 6
Paaren
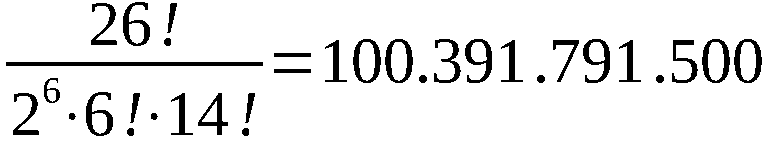
Und bei zehn Paaren
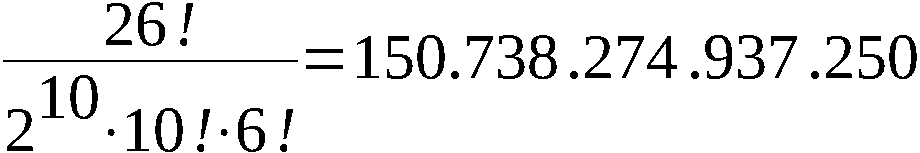
Die Zahl verschiedener Schaltungen für die Umkehrwalze
beträgt

Und für die übrigen Walzen
26! = 403.291.587.620.262.925.584.000.000
Die letzte Zahl kann man sich folgendermaßen veranschaulichen:
Wenn sämtliche die Erdkugel bewohnenden Menschen in jeder Se-
kunde je eine Schaltung ausführen würden, so würden sie ihre
Arbeit erst nach sechs Milliarden Jahren beenden (wobei neben-
bei bemerkt werden möge, daß angeblich die Welt erst seit 2
Milliarden Jahren existiere).
9. Auffindung der Spruchschlüssel
Folgendes Problem ist bisher gelöst worden: Bei Kenntnis der
Schlüssel für zwei Monate die Walzenschaltungen auffinden.
Damit ist jedoch die Aufgabe nicht beendet. Es handelt sich
vielmehr jetzt um die Lösung des umgekehrten Problems: Bei
bekannten Walzenschaltungen die Schlüssel finden.
Zunächst wurde im technischen Büro der polnischen Schlüssel-
stelle die Enigma vom Handelstyp so umgeändert, daß sie zum
Lesen von Militärsprüchen dienen konnte. Daraufhin wurde das
Spruchmaterial für zwei Monate, für die Schlüssel vorhanden
waren, gelöst und hierbei eine Reihe von Fehlern, die von den
Schlüsslern begangen wurden, entdeckt und natürlich ausgenutzt.
Diese Fehler dienten vor allem zur Auffindung der Spruchschlüs-
sel d.h. der Schlüssel, die von Chiffranten willkürlich gewählt, // Chiffranten = Chiffreure
zweimal geschlüsselt und daraufhin am Anfang des Spruches
eingesetzt werden. Im Laufe der Jahre gelang es zwar den Deu-
tschen, ihr Schlüsselpersonal so zu schulen, daß immer we-
niger Fehler begangen wurden, die Entwicklung in dieser Rich-
tung ging jedoch genügend langsam von statten, so daß es stets
gelang, in der Zwischenzeit immer raffiniertere Methoden aus-
zusinnen, um trotz allem die Spruchschlüssel auffinden zu
können.
10. Methode der charakteristischen Schlüssel
In der ersten Zeit nach Einführung der Enigma wählten die
Schlüssler mit Vorliebe solche Schlüssel, die aus 3 gleichen
Buchstaben bestanden wie AAA, BBB, u.s.w. Die Methode der
charakteristischen Schlüssel beruhte nun darauf, mit Hilfe
der Zyklentheorie die einzelnen Zyklen so einander zuzuordnen,
um möglichst viele aus drei gleichen Buchstaben bestehenden
Schlüssel zu erhalten. Bald jedoch wurde den Schlüsslern die
Wahl dreier gleicher Buchstaben verboten. Daraufhin begannen
sie, sich solche Buchstaben zu wählen, die sich auf dem Glüh-
lampenfeld der Maschine
Q W E R T Z U I O
A S D F G H J K
P Y X C V B N M L
quer oder waagerecht nebeneinander befinden, wie ASD, QAY,
QWE, u.s.w. Es genügte jetzt die Zyklen so einander zuzuord-
nen, daß möglichst viele Schlüssel wie ASD u.s.w. entstanden.
11. Die statistische Methode
Bald aber wurde auch das verboten. Inzwischen bemerkte man
jedoch, daß die Buchstaben des Alphabets in den Schlüsseln
nicht mit gleicher Häufigkeit auftraten. So zum Beispiel tra-
ten auf als erste Buchstaben in den Schlüsseln vor allem Buch-
staben A und Q, als zweite Buchstaben sämtliche Vokale, als
dritte Buchstaben die Buchstaben L und O. Andere Buchstaben
dagegen wie J oder Y kamen nur selten vor. Man verfertigte
also eine Statistik der Buchstabenfrequenzen und bemühte sich
dann, die Zyklen so einander zuzuordnen, um eine möglichst
gute Übereinstimmung mit der Statistik zu erzielen. Die Buch-
stabenfrequenzen schwankten übrigens im Laufe der Zeit, so
daß ab und zu die Statistik verändert werden mußte. Auch
waren die Buchstabenfrequenzen andere im Heer und andere in
der Luftwaffe. Im Sicherheitsdienst wurden die Schlüssel so
sorgfältig gewählt, daß sämtliche Buchstaben mit derselben
Frequenz auftraten und die statistische Methode also nicht
angewandt werden konnte.
12. Methode ungleicher Buchstaben
Nach dem Verbot, drei gleiche Buchstaben als Schlüssel zu wählen,
vermieden die Schlüssler aufs sorgfältigste selbst solche Schlüs-
sel, in denen auch nur zwei gleiche Buchstaben auftraten, wie
AAB oder FVF. Dieses Merkmal war das beständigste von allen
und hat sich zum heutigen Tage erhalten. Die auf diesem Merk-
mal aufgebaute Methode hatte den Vorteil, daß man oft ganz
mechanisch vorgehen konnte.
Nehmen wir etwa an, am gegebenen Tage hätten wir Zyklen von
folgender Gestalt:
(SAIZELWDPBOHU)(YCRKXFJQNGVMT)
(AZHNUGWMSFLR)(QBYKPDEVJIOT)(C)(X)
(AZCSYBVMFJPDO)(NUGTIRHQKXEWL)
Wir haben dann nebenstehende Figur und zwei analoge Figuren
aufzuzeichnen und hierauf in den leeren Rechtecken diejenigen
Zuordnungen von Zyklen zu streichen, die Gleichheit zweier
Buchstaben nach sich ziehen würden.
| S | TYCRKXFJQNGVM |
| A | MTYCRKXFJQNGV |
| I | VMTYCRKXFJQNG |
| Z | GVMTYCRKXFJQN |
| E | NGVMTYCRKXFJQ |
| L | QNGVMTYCRKXFJ |
| W | JQNGVMTYCRKXF |
| D | FJQNGVMTYCRKX |
| P | XFJQNGVMTYCRK |
| B | KXFJQNGVMTYCR |
| O | RKXFJQNGVMTYC |
| H | CRKXFJQNGVMTY |
| U | YCRKXFJQNGVMT |
| AZHNUGWMSFLR | |
| TOIJVEDPKYBQ | |
| QTOIJVEDPKYB |
| BQTOIJVEDPKY |
| YBQTOIJVEDPK |
| KYBQTOIJVEDP |
| PKYBQTOIJVED |
| DPKYBQTOIJVE |
| EDPKYBQTOIJV |
| VEDPKYBQTOIJ |
| JVEDPKYBQTOI |
| IJVEDPKYBQTO |
| OIJVEDPKYBQT |
| C |
| X | |
Wenn man über genügende Anzahl von Sprüchen verfügt, wird
schließlich nur ein Fall übrig bleiben.
13. Bestimmung der rechten Walze
Nachdem man so in den meisten Fällen in der Lage war, die
Spruchschlüssel wiederherzustellen, trat man jetzt zur Auf-
findung der Tagesschlüssel, d.h. Walzenlage, Steckerverbin-
dung, Ringstellung, Grundstellung. Man begann mit der Bestim-
mung der Walzenlage.
Wenn man zwei beliebige deutsche Sätze, jeder hundert Buch-
staben lang, untereinander schreibt, so werden durchschnitt-
lich in 8 Kolonnen je zwei gleiche Buchstaben auftreten.
Diese Eigenschaft bleibt auch dann bestehen, wenn man beide
Sätze nach einem und demselben Verfahren verschlüsselt. Nimmt
man dagegen zwei sinnlose Texte, zu je 100 Buchstaben, in
denen sämtliche Buchstaben mit etwa derselben Frequenz auf-
treten und schreibt sie untereinander, so wird man im Durch-
schnitt nur 4 Kolonnen mit je zwei gleichen Buchstaben antref-
fen. Diese Eigenschaft benutzt man, um die rechte Walze zu be-
stimmen. Wenn man nämlich über genügendes Spruchmaterial ver-
fügt, so wird man eine Anzahl Paare von Sprüchen finden, der-
art, daß in jeder Paar die ersten sowie die zweiten Buchstaben
der Schlüssel einander gleich, die dritten Buchstaben dagegen
voneinander verschieden sind. Man schreibt nun die beiden
Sprüche eines Paares so untereinander, daß Buchstaben, die
bei der gleichen Position der Walzen geschlüsselt wurden,
senkrecht untereinander zu stehen kommen. A priori sind jedoch
zwei Fälle möglich, je nachdem, wann die Drehung der mittleren
Walze erfolgt. Man zählt also nach, wieviel Kolonnen mit glei-
chen Buchstaben in beiden Fällen vorkommen und muß im rich-
tigen Falle, im Allgemeinen wenigstens, etwa zweimal so viel
Kolonnen erhalten als im falschen Fall. Man erfährt hierdurch,
in welchem Intervall die mittlere Walze sich dreht, und, wenn
man so mit sämtlichen Paaren verfährt, wird man fast stets
das Intervall so einengen können, daß hierdurch die rechte
Walze, die ja die Drehung der mittleren Walze bewirkt, eindeu-
tig bestimmt wird. Die übrigen Walzen bestimmt man später auf
andere Weise.
14. Der Rost
Die nächste Arbeitsphase bestand in der Auffindung der Stecker-
verbindungen. Es war dies ein ziemlich schwieriges Problem,
doch schließlich ersann man eine Methode, die davon ausging,
daß erstens während des Schlüsselns des Spruchschlüssels eine
Drehung der mittleren Walze nur etwa in 5 Fällen eintritt,
und daß zweitens die Steckerverbindung eine Anzahl Buchstaben
unverändert läßt.
Zur Veranschaulichung der Methode stellen wir uns zunächst
einmal vor, die Steckerverbindung sei nicht vorhanden. Dann
kann man die sechs Gleichungen für die Substitutionen A1 bis
A6 auf folgende Gestalt bringen:

In diesen Gleichungen ist alles bekannt mit Ausnahme von
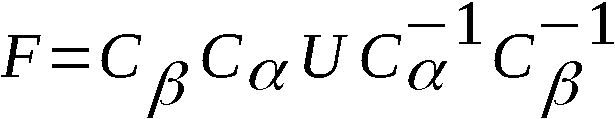 und des Exponenten X. Denn wenn wir
auch dank der vorliegenden Methode wissen, welche Walze sich
auf der rechten Seite befindet, so wissen wir doch nicht,
welches ihre Position ist.
Wir verfahren also auf die Weise, daß wir für X der Reihe
nach die Werte von 0 bis 25 einsetzen und jedesmal F aus jeder
der sechs Gleichungen errechnen. Die sechs Substitutionen F
werden jedesmal untereinander verschieden seines mit Ausnahme
einzigen Falles, wo sie sämtlich denselben Wert annehmen.
Auf diese Weise erhalten wir X, d.h. die Position der rechten
Walze und zugleich auch die Substitution F, die wir noch spä-
ter benötigen werden.
In der Praxis geht man in der Weise vor, daß man auf einem
Bogen Papier der Reihe nach die zweiten Zeilen der Substitu-
tionen
und des Exponenten X. Denn wenn wir
auch dank der vorliegenden Methode wissen, welche Walze sich
auf der rechten Seite befindet, so wissen wir doch nicht,
welches ihre Position ist.
Wir verfahren also auf die Weise, daß wir für X der Reihe
nach die Werte von 0 bis 25 einsetzen und jedesmal F aus jeder
der sechs Gleichungen errechnen. Die sechs Substitutionen F
werden jedesmal untereinander verschieden seines mit Ausnahme
einzigen Falles, wo sie sämtlich denselben Wert annehmen.
Auf diese Weise erhalten wir X, d.h. die Position der rechten
Walze und zugleich auch die Substitution F, die wir noch spä-
ter benötigen werden.
In der Praxis geht man in der Weise vor, daß man auf einem
Bogen Papier der Reihe nach die zweiten Zeilen der Substitu-
tionen  folgendermaßen aufschreibt:
(die ersten Zeilen der Substitutionen würden stets lauten
1 2 3 4 … 26)
7 19 3 15 23 11 20 4 16 26 10 14 22 2 17 6 25 9 1 21 12 18 5 24 13 8
16 2 14 22 10 19 3 15 25 9 13 21 1 16 5 24 8 26 20 11 17 4 23 12 7 6
1 13 21 9 18 2 14 24 8 12 20 26 15 4 23 7 25 19 10 16 3 22 11 6 5 17
: :
(das Beispiel ist willkürlich)
Hierauf schreib man auf einem zweiten Bogen mit Öffnungen
(daher der Name Rost) die 6 Substitutionen A1 bis A6 in fol-
gender Form auf:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
V T Z F K D R N O U E W Y H I S X G P B J A L Q M C
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
K Q H U V S Z C O N A T W J I Y B X F L D E M R P G
Nach diesen Vorbereitungen legt man den Rost auf den ersten
Bogen und verschiebt ihn so lange von oben nach unten, bis in
einer bestimmten Lage die in Öffnungen erscheinenden Substi-
tutionen F sämtlich identisch sind. Das trifft natürlich nur
dann ein, wenn keine Steckerverbindungen vorhanden sind. Im
entgegengesetzten Fall ändert sich das Bild, da jedoch die
Steckerverbindungen nicht sämtliche Buchstaben vertauschen,
wird man in einer bestimmten Lage gewisse Analogien zwischen
den 6 verschiedenen Substitutionen F bemerken. Man muß nun
versuchen, die Buchstaben der Substitutionen A1 bis A6 so um-
zustellen, daß alle F identisch werden. Gelingt dies, so er-
geben die Umstellungen der Buchstaben die gesuchten Stecker-
verbindungen, und zugleich erhält man die Position der rechten
Walze sowie die Substitution F.
15. Der Katalog F
Nachdem so die rechte Walze und ihre Position bereits bekannt
war, hätte man die linke und mittlere Walze und ihre Positionen
einfach so bestimmen können, daß man direkt auf der Maschine
sämtliche möglichen Fälle probierte. Um sich jedoch dieselbe
unnütze Arbeit zu ersparen, verfertigte man ein- für allemal
einen Katalog, der sämtliche möglichen Substitutionen F,
deren es
6 · 26 · 26 = 4056
gibt, enthielt. Es genügte jetzt die Substitution F, die man
beim Suchen der Steckerverbindungen erhalten hatte, im Kataloge
nachzuschlagen, um sofort Lage und Stellung der linken und
mittleren Walze zu erfahren.
16. Der Zyklometer
Die Methode, die man anwandte, um die Steckerverbindungen zu
finden, war nicht nur lang und umständlich, sondern sie führte
auch nicht immer zum Ergebnis. Übrigens setzte sie die Kenntnis
des Spruchschlüssel voraus, und die Methoden, diese Schlüssel
zu finden, waren ebenfalls zeitraubend und nicht immer vom
Erfolg gekrönt. So sah man sich denn nach anderen Methoden um,
die schneller und sicherer zum Ziele führen könnten. Man ver-
fiel darauf, daß die Gestalt der Zyklen erstens invariant ge-
genüber den durch die Steckerverbindungen verursachten Substi-
tutionen sei, und zweitens ein Charakteristikum des betref-
fenden Tages bildete, in dem Sinne nämlich, daß zwei Tage deren
Zyklen die gleiche Gestalt hatten, verhältnismäßig selten
vorkommen konnten. So kam man denn auf den Gedanken, die Zyklen
in sämtlichen möglichen Positionen der Walzen, deren es bei
drei Walzen, wie bereits gesagt,
105.456
gab, zu katalogisieren. Um diese Arbeit zu bewältigen, baute
man eine besondere Maschine, den Zyklometer, der aus zwei
Enigmen bestand, die so gekoppelt waren, daß in jeder Position
eine größere oder kleinere Anzahl der Glühlampen gleichzeitig
aufleuchtete, je nach der Länge des entsprechenden Zyklus.
Mehr als ein Jahr verging, ehe die Arbeit beendet war, dann
aber fand man in der Regel schon nach wenigen Minuten Walzen-
lage, Position der Walzen und Steckerverbindungen des betref-
fenden Tages.
17. Grundstellung und Ringstellung
Unter Position der Walzen verstehen wir stets die Differenz
zwischen Grund- und Ringstellung. Um also den völligen Besitz
des Tagesschlüssels zu gelangen, mussten noch die beiden letzten
Elemente des Tagesschlüssels, d.h. Grund- und Ringstellung
gefunden werden. Dazu genügt es offenbar nicht, sich auf das
Studium der Spruchschlüssel zu beschränken, vielmehr muß auf
den Inhalt der Sprüche zurückgegriffen werden.
Als man das Material von Oktober und Dezember 1931, für das
Schlüssel vorhanden war, löste, bemerkte man, daß der Text
sehr vieler Sprüche mit Buchstaben AN begann.
Um also Grund- und Ringstellung gesondert zu erhalten, nahm
man irgendeinen Spruch, von dem man vermutete, daß er mit
Buchstaben AN begann und probierte in sämtlichen Positionen
der Maschine, ob diese Annahme möglich ist. Eine langwierige
Arbeit, wenn man bedenkt, daß dabei 263 = 17.576 Positionen
untersucht werden müssen.
Später überzeugte man sich, daß, wenn ein Spruch mit den Buch-
staben AN begann, a priori gewisse Positionen der rechten Walze
unmöglich waren. Und da man täglich über eine ganze Anzahl von
Sprüchen verfügte, in denen man ein AN am Anfang erhofft durfte,
so gelang es meistens rein rechnerisch die richtige Position
der rechten Walze zu erhalten.
18. Einige Bemerkungen
Bei der Beschreibung des Rostes und des Zyklometers wurde vor-
ausgesetzt, daß während des Schlüsselns des Spruchschlüssels
die mittlere Walze sich nicht drehte. In Wirklichkeit ist
diese Voraussetzung nicht bedingt erforderlich, ja die Auf-
findung von Grund- und Ringstellung ist sogar besonders leicht
gerade dann, wenn eine Drehung der mittleren Walze eintritt.
Wir überlassen es dem Leser zu ermitteln, wie sich in solchen
Fällen die Verhältnisse gestalten.
Man hat bemerkt, daß innerhalb eines Tages die sechs Grund
und Ringstellung bildenden Zahlen bzw. Buchstaben stets von-
einander verschieden waren. Diese Feststellung führte nicht
nur in gewissen Fällen zu bedeutender Vereinfachung der Arbeit,
sondern sie erlaubte es auch in späteren Jahren die Methode
Herivel, von der noch die Rede sein wird, zweckmäßig anzu-
wenden. Es gab übrigens auch Zeiträume, wo gar stets in vier
aufeinander folgenden Tagen alle 24, die Grund- und Ringstel-
lungen bildenden Zahlen bzw. Buchstaben voneinander verschie-
den waren.
Ähnliche Entdeckungen hat man zu verschiedenen Zeiten auch
mit den Steckerverbindungen gemacht.
19. Neue Netze. Beständige Änderungen
Im Maße wie sich die deutsche Wehrmacht entwickelte, wurde
auch die Zahl der Heeresfunkstellen immer mehr vergrössert.
Dabei wurde allmählich ebenfalls die Zahl der Funknetze, die
sich alle derselben Enigma, jedoch mit anderen Tagesschlüssel
bedienten, vermehrt. So bildete z.B. die neugegründete deu-
tsche Luftflotte mit dem 1. August 1935 ihr eigenes Funknetz
mit eigenem Tagesschlüssel.
Um die Unauflösbarkeit des Enigmaverfahrens sicherzustellen,
wurden verschiedene Neuerungen eingeführt. Ab 1. Februar 1936
wurde die Walzenlage monatlich, und ab 1. Oktober 1936 sogar
täglich geändert. Gleichzeitig wurde die Zahl der Steckerver-
bindungen geändert, sie betrug nicht mehr als 6, wie bisher,
sondern 5 bis 8. Und schließlich wurde noch am 2. November 1937
die bisherige Umkehrwalze aus dem Verkehr genommen und durch
eine neue, die sogenannte Umkehrwalze B, ersetzt.
20. Umkehrwalze B
Von Seiten der deutschen Schlüssler wurde die Unvorsichtigkeit
begangen, in den Funksprüchen vom September 1937 von der be-
vorstehenden Änderung der Umkehrwalze zu reden. So war man denn
in der polnischen Schlüsselstelle auf die Änderung vorbereitet
und wunderte sich nicht, als die Gestalt der Zyklen vom 2. No-
vember 1937 im Kataloge nicht aufzufinden war. Dagegen konnte
man natürlich nach wie vor mit Hilfe des Rostes die Stecker-
verbindungen sowie die rechte Walze und ihre Position bestimmen.
Unbekannt blieben nur die linke und mittlere Walze sowie ihre
Positionen. Das ergab 2 · 26 · 26 = 1352 mögliche Fälle und
jeder dieser Fälle bestimmte eine Umkehrwalze. Durch Vergleich
dieser 1352 Umkehrwalzen in zwei verschiedenen Tagen konnte
leicht die richtige Umkehrwalze ermittelt werden.
21. Neue Chiffrierwalzen
Im September 1937 bildete sich ein neues Funknetz, nämlich
das Funknetz des Sicherheitsdienstes, einer politischen Orga-
nisation, von der noch später die Rede sein wird. Das Schlüs-
selverfahren war in diesem Netze im Großen und Ganzen dasselbe,
wie in der Armee, jedoch wurden gewisse Neuerungen nicht gleich-
zeitig, sondern mit einer bestimmten Verspätung eingeführt.
So z.B. wurde am 15. September 1938 das Schlüsselverfahren im
Heere und in der Luftwaffe vollständig umgeschaltet, dagegen
blieb es im Sicherheitsdienst noch mehrere Monate lang unver-
ändert, ein grober Fehler, der sich sofort rächen sollte.
Denn bereits drei Monate später wurden, diesmal gleichzeitig
in allen Netzen, zwei neue Chiffrierwalzen, die Walzen IV und
V eingeführt. Da in diesem Augenblicke das Netz des Sicher-
heitsdienstes sich noch des alten Verfahrens bediente, kon-
nten die Schaltungen dieser Walzen in ähnlicher Weise gefunden
werden, wie die Schaltungen der Umkehrwalze B. Es erübrigt
sich wohl, in Einzelheiten einzugehen, es möge nur angedeutet
werden, daß man sich hierbei zweier Tage, in denen Drehung
der mittleren Walze eintrat, bediente. Wäre im Sicherheits-
dienst das neue Chiffrierverfahren früher eingeführt worden,
so hätte man wohl kaum die Schaltungen der Walzen IV und V
auf kryptologischem Wege erhalten.
22. Änderung des Chiffriersystems
Dank der beschriebenen Methoden konnten bis September 1938
tagtäglich sämtliche Netze d.h. Heer, Luftwaffe, Sicherheits-
dienst, Marine (von der noch weiter unten die Rede sein wird)
in oft unglaublich kurzer Zeit gelöst werden.
Die Sachlage änderte sich jedoch vollkommen, als am 15. Sep-
tember 1938 ein neues Chiffrierverfahren eingeführt wurde und
hierdurch die bisherigen Errungenschaften polnischer Krypto-
logen auf diesem Gebiete ernsthaft bedroht wurden.
Das neue Schlüsselverfahren beruhte darauf, daß die Grundstel-
lung nicht mehr eine und dieselbe war für sämtliche Sprüche
eines Tages, sondern von Spruch zu Spruch wechselte.
Wir wollen das neue Schlüsselverfahren an einem Beispiele er-
läutern. Der Schlüssler wählt sich zwei Buchstabentripel, z.B.
SKR WTC, stellt die Maschine auf SKR ein und schlüsselt die
Buchstaben WTC zweimal hintereinander (wie bisher), wobei
etwa die sechs Buchstaben KFDLSF erhalten möge.
Die Grundstellung SKR wird unverschlüsselt in den Kopf des
Spruches, die sechs Buchstaben KFD LSF am Anfang des Spruches
eingesetzt, und der Spruch selbst wird von der Stellung WTC
aus verschlüsselt (also so wie bisher). Daß das neue Verfahren
gerade so, wie beschrieben, und nicht anders war, erfuhr man
dadurch, daß bereits am Vortage der Systemänderung einige
Schlüssler sich des neuen Verfahrens bedienten, was natür-
lich ein grober Fehler war.
23. Auffindung der Walzenlage
Da bei dem neuen System die Spruchschlüssel nicht mehr von
ein- und derselben Position aus verschlüsselt werden, so wurde
die Zyklentheorie und die darauf aufgebauten Methoden der
Spruchschlüssels, des Rostes und des Zyklometers hinfällig.
Man ließ jedoch die Arme nicht hängen, sondern schritt zur
Untersuchung des neuen Verfahrens. Als erstes stellte man fest,
daß wenn das Spruchmaterial innerhalb eines Tages und eines
Netzes genügend umfangreich war, man von Zeit zu Zeit auf
Paare von Grundstellungen traf, deren erste und zweite Buch-
stabe identisch, und deren dritte Buchstaben im Alphabet neben-
einander oder fast nebeneinander standen, wie etwa TKP und TKR.
Wenn dann zufälligerweise auch in den Spruchschlüsseln gleiche
Buchstaben an entsprechenden Stellen auftraten, so konnte man
hieraus bisweilen schlußfolgern, welche Walzen sich rechts oder
in der Mitte befinden. Wir wollen die verschiedenen Möglichkei-
ten an einigen Beispiele klarmachen.
1) Angenommen, wir hätten zwei Sprüche mit folgenden Schlüsseln
gefunden:
Grundstellung Spruchschlüssel
TKP ANV CKB
TKR VTS JQM
In diesem Fall ist sicher, daß zwischen Buchstaben P und R
eine Drehung der mittleren Walze stattfindet, d.h. daß rechts
sich die Walze I befindet, da diese und nur diese eine Drehung
zwischen Q und R hervorruft. Im entgegengesetzten Falle würden
den gleichen Buchstaben V auch gleiche Buchstaben B (oder J)
entsprechen.
2) Grundstellung Spruchschlüssel
TKP ANV CKB
TKR VTS BQM
In diesem Falle ist es wenig wahrscheinlich, daß eine Drehung
zwischen P und R eintritt, daß also rechts sich die Walze I
befindet.
3) Auch Grundstellungen mit verschiedenen mittleren Buchstaben
können Aufschlüsse über die Walzenlage bieten, wie folgendes
Beispiel zeigt:
Grundstellung Spruchstellung
TKP ANV CKB
TLR VTS JQM
Zwischen P und R kann keine Verschiebung der mittleren Walze
eintreten, also ist die rechte Walze sicher verschieden von
der Walze I.
4) Ja sogar aus Grundstellungen mit verschiedenen ersten Buch-
staben lassen sich bisweilen Schlüsse über Walzenlage ziehen.
Grundstellung Spruchschlüssel
TJG CES PKR
UKG CNT PLJ
In diesem Falle ist es wahrscheinlich, daß zwischen J und K
sich die linke Walze gedreht hat, daß also in der Mitte sich
die Walze IV befindet. In anderen Fällen lassen sich ähnliche
Schlüsse ziehen.
24. Bomben
Bereits wenige Tage nach Einführung des neuen Schlüsselverfah-
rens hatte man einen Plan gefaßt, wie man die entstandenen
Schwierigkeiten aus dem Wege schaffen könnte. Unser Ideengang
war folgender:
Nehmen wir eine Anzahl von Sprüchen und schreiben deren Grund-
stellungen und Spruchschlüssel auf.
1. KTL WOC DRB 7. GRA FDR YWD
2. SVW KKM IYS 8. MDO OTW YZW
3. JOT IWA BWN 9. KJC FSW RSE
4. EDC DSP LJC 10. SGF TEY ASR
5. GDK WAV WHA 11. AGH MDF RHF
6. BWK TCA TOC 12. JBR WLT SOQ
Richten wir jetzt unsere Aufmerksamkeit auf den Spruch Nr. 3.
In dessen Spruchschlüssel kommt der Buchstabe W zweimal im Ab-
stande von 3 Buchstaben vor. Das bedeutet, daß in einer ganz
bestimmten Position der Maschine der Buchstabe W einen uns un-
bekannten Buchstaben, sagen wir etwa X, ergeben und drei Po-
sitionen später derselbe Buchstabe W wieder denselben Buch-
stabe X ergeben würde. Nehmen wir nun noch an, der Buchstabe W
werde durch Steckerverbindungen nicht berührt, eine Annahme,
die bei 5 bis 8 Steckerverbindungen in 50% aller Fälle zutref-
fend ist.
Dann könnte man die richtige Position der Walzen ermitteln,
daß in zwei Maschinen, deren Positionen sich um 3 unterschei-
den, der Buchstabe W gleichzeitig getastet und daraufhin in
beiden Maschinen die Walzen synchronisch gedreht werden. Jedes-
mal, wenn in beiden Maschinen gleichzeitig derselbe Buchstabe
aufleuchtet, haben wir es mit einem Fall zu tun, der möglicher-
weise richtig ist und daher besonders untersucht werden muss.
Da jedoch solche Fälle allzu häufig auftreten würden, hilft
man sich in der Weise, daß man nicht einen, sondern drei Sprü-
che, in deren Spruchschlüssel der Buchstabe W zweimal im Ab-
stande von 3 Buchstaben vorkommt, benutzt. In unserem Beispiel
wären es Sprüche Nr. 3, 5 und 8. Nur muß man sich natürlich
nicht zweier, sondern sechs Maschinen bedienen. Es wäre aber
in Wirklichkeit höchst umständlich und unzweckmäßig, wollte
man wirklich mit sechs einzelnen Maschinen manipulieren. Viel-
mehr man eine Maschine, Bombe genannt, die 6 Enigmen entsprach,
elektrisch angetrieben wurde und jedesmal automatisch anhielt,
wenn ein günstiger Fall vorlag. Es wurden in der polnischen
Schlüsselstelle sechs solche Bomben montiert, für jede Walzen-
lage eine (denn die Walzen IV und V wurden erst später einge-
führt), wobei jede Bombe alle möglichen 17.576 Fälle in 1,5
Stunden bewältigte.
25. Die Netze
Die Bomben befanden sich noch im Bau, als bereits neue Ände-
rungen eintraten. Am 15. Dezember 1938 wurden die Walzen IV
und V eingeführt, die Anzahl der möglichen Walzenlagen also
verzehnfacht, und zwei Wochen später die Zahl der Steckerver-
bindungen auf 7 - 10 erhöht. Durch diese Änderungen verloren
die Bomben praktisch den größten Teil ihrer Bedeutung, da
die Lösung eines Tages zu viel Zeit beanspruchen würde. Es
gelang zwar bisweilen, dank der früher angegebenen Methode
die Walzenlage teilweise zu bestimmen, aber nur dann, wenn
umfangreiches Material vorhanden war, was verhältnismäßig
selten eintrat. Auch war die Anwendbarkeit der Bomben durch
die Steckerverbindungen eingeschränkt.
Man schuf daher bereits sehr früh eine neue Methode, die von
der Zahl der Steckerverbindungen unabhängig war.
Zur Darlegung dieser neuen Methode müssen wir zunächst einen
neuen Begriff, den der männlichen und weiblichen Positionen,
einführen. Kehren wir noch einmal zu den Sprüche zurück:
1. KTL WOC DRB 7. GRA FDR YWD
2. SVW KKM IYS 8. MDO OTW YZW
3. JOT IWA BWN 9. KJC FSW RSE
4. EDC DSP LJC 10. SGF TEY ASR
5. GDK WAV WHA 11. AGH MDF RHF
6. BWK TCA TOC 12. JBR WLT SOQ
Ein Fall, wie im Spruchschlüssel Nr. 3, daß derselbe Buchstabe
(in unserem Beispiel W) zweimal im Abstand von drei Buchstaben
vorkommt, kann nicht in sämtlichen Positionen der Maschine
eintreten. Vielmehr haben Rechnungen ergeben, daß solche Fäl-
le in etwa 40% aller Positionen eintreten (genau genommen be-
trägt das Verhältnis 1 - (1/√e), wobei e die Basis der
natürlichen Logarithmen ist). Diese Positionen nennen wir
weibliche Positionen, die übrigen heißen männliche Positionen.
In unserem Beispiel gehören die sechs Sprüche Nr. 3, 5, 6, 8,
9, 11 bestimmt weiblichen Positionen an, während von den
übrigen Sprüchen nichts ausgesagt werden kann. Die Stecker-
verbindungen haben natürlich Einfluß auf die in den Spruch-
schlüsseln auftretenden Buchstaben, nicht aber auf das Ge-
schlecht der Position (ob weiblich oder männlich).
Man konnte daher einen Katalog mit sämtlichen weiblichen Po-
sitionen anfertigen, und in diesem Kataloge nachsuchen, ob
man nicht sechs weibliche Positionen findet, die in denselben
Abständen auftreten, wie die Grundstellungen: JOU, GKD, BWK,
MDR, KJD, AGK (dabei müssen auch eventuell Drehungen der mit-
tleren wie auch linken Walze berücksichtigt werden).
Da dies jedoch praktisch unausführbar wäre, so ging man anders
vor; man stellte die sogenannte Netze her: Für jede Walzenlage
werden sämtliche weibliche Positionen auf 26 Bogen Papier,
von denen jeder 26x26 Felder, und zwar in vierfacher Ausfüh-
rung enthält, eingetragen. Die verschiedenen Bogen entsprechen
den 26 Positionen der linken Chiffrierwalze, die 26x26 Felder
der mittleren und rechten Walze. Der Grund der vierfachen Aus-
führung wird unten erklärt werden. Die Felder die den weib-
lichen Positionen entsprechen, werden durchlocht (daher der
Name Netz).
Nun werden, um auf unseres Beispiel zurückzugehen, sechs von
den 26 Bogen in einer Reihenfolge und in einer Lage, die den
gegenseitigen Entfernungen der Grundstellungen entspricht,
aufeinander gelegt. Wenn gleichzeitig in allen sechs Bogen an
derselben Stelle ein Loch erscheint, so haben wir es mit einem
möglicherweise richtigen Falle zu tun, der besonders geprüft
werden muß. Um alle möglichen Fälle zu erschöpfen, müssen die
Bogen der Reihe nach zyklisch vertauscht werden. Auf jedem
Bogen befinden sich die 26x26 Felder in vierfacher Ausführung,
weil die Bogen nicht direkt, sondern gegenseitig verschoben
aufeinander gelegt werden. Die Erzielung des Ergebnisses ist
von einem überaus sorgfältigen Aufeinanderlegen der Bogen in
der richtigen Lage abhängig. Deshalb wurde stets vor Beginn
der Arbeit auf einem besonderen Zettel, dem sogenanntem Menu,
die Reihenfolge und gegenseitige Lage der Bogen festgelegt.
Die Kenntnis, welche Positionen weiblich und welche männlich
sind, wurde den Katalogen zum Zyklometer entnommen, denn offen-
bar entsprechende weibliche Positionen denjenigen Substitutionen,
in denen Zyklen vorkommen, die aus einem Buchstabe bestehen.
Das Prüfen der richtigen Fälle geschah auch mit Hilfe des
Zyklometers. Da dies ziemlich zeitraubend war, trug man sich
mit dem Gedanken, besondere Kataloge herzustellen, in denen
nicht nur die weibliche Positionen, sondern auch alle Buch-
staben, die in den eingliedrigen Zyklen vorkommen, eingetragen
wären. Aber dieser Gedanke wurde erst später, und zwar von der
englischen Schlüsselstelle, verwirklicht.
26. Die Warschauer Konferenz
In der Polnischen Schlüsselstelle wurden zwei Sätze von je 26
Netzen für zwei Walzenlagen mit der Hand angefertigt, und man
überzeugte sich daß die Idee der Netze vollkommen brauchbar
ist. Ganz anders jedoch stellte sich die Ausführung dieser
Idee dar.
Während die weiblichen Positionen für die Walzenlagen I II III,
I III II, …, III II I direkt von den Katalogen entnommen wer-
den konnten, müßte man für die übrigen 54 Walzenlagen die
weibliche Positionen erst ermitteln, entweder mittels des Zy-
klometers, was mehrere Jahre beansprucht hätte, oder mit Hilfe
einer neuen kostspieligen Maschine, woran man zunächst noch
nicht denken wollte. Ferner war das handmäßige Perforieren
bereits der beiden ersten Sätze von je 26 Netzen recht mühsam
gewesen, so daß man für den Rest der Arbeit ebenfalls beson-
dere Apparate benötigt haben wäre. Und schließlich wäre, wenn
schon alles fertig wäre, das Manipulieren mit den 60 Sätzen
von Netzen, um die einzelnen Tage zu lösen, ein zahlreiches
Hilfspersonal erfordern.
Da die polnische Schlüsselstelle nicht in der Lage war, all
diese Schwierigkeiten selbst zu bewältigen, entschloss man
sich, das Geheimnis der Enigma, das bisher sorgsam gehütet
war, auch der französischen und englischen Schlüsselstellen
anzuvertrauen.
Am 26. Juli trat in Warschau eine dreitägige Konferenz unter
Teilnahme von Vertretern der französischen und englischen
Schlüsselstelle in Sachen der Enigma zusammen. Es stellte
sich heraus, daß weder unsere französischen noch englischen
Fachgenossen die ersten Schwierigkeiten haben überwinden
können. Die Walzenschaltungen waren ihnen unbekannt, mithin
auch etwaige Auflösungsmethoden. Wir legten ihnen die Ergeb-
nisse unserer siebenjährigen Arbeit, sowie die Schwierigkeiten,
auf die wir zuletzt gestoßen waren, vor. Von Seiten der En-
gländer wurde bereitwilligst Hilfe in der Ausführung der Netze
für die 60 Walzenlagen versprochen.
27. Kriegsaufbruch. Vignolles
Ein Monat später brach der deutsch-polnische Krieg aus. Es ge-
lang noch, den 25. August 1939, den Tag der allgemeinen Mobil-
machung in Deutschland, zu lösen, als bereit die Evakuierung
begann. Die Bomben, Zyklometer, Enigmen, Netze, sämtliche Akten
und Aufzeichnungen wurden mitgenommen, aber auf dem Wege zur
rumänischen Grenze vernichtet. Einzig und allein zwei Enigmen
wurden gerettet. In Bukarest nahm sich der drei Spezialisten
von der Enigma die französische Botschaft an und schickte sie
sofort nach Paris, wo sie gastfreundlich aufgenommen wurden.
Einige Wochen später schuf der französische Generalstab in
Vignolles, einem Schlößchen unweit Gretz, 30 km von der Haupt-
stadt entfernt, ein Büro, wo polnische Kryptologen samt Hilfs-
personal unter Leitung von Oberstleutnant Langer versuchten,
die in Polen unterbrochene Arbeit wiederaufzunehmen. Man be-
gann wieder mühselig, wie bereits schon einmal in Warschau,
die Netze mit der Hand zu fabrizieren, eine Arbeit, die wohl
erst nach Jahren beendet worden wäre.
Jetzt aber begann die Warschauer Konferenz Früchte zu tragen.
Es stellte sich heraus, daß in der Zwischenzeit die Engländer
eine Maschine konstruiert hatten, die ihnen ermöglichte, die
Netze für sämtliche 60 Walzenlagen in wenigen Wochen herzu-
stellen. Aber Proben, die mit diesen Netzen in England ange-
stellt wurden, gaben kein Ergebnis. Da glücklicherweise die
Netze in zwei Exemplaren hergestellt waren, konnten uns die
Engländer ein Exemplar zur Verfügung stellen, was sie auch
freundlichst taten. Sobald diese Netze in Vignolles ankamen,
begann eine angestrengte Arbeit, und bald waren zwei Tage,
der 28.10.1939 und der 6.1.1940 gelöst werden würde.
Die Engländer haben ihre Arbeit glänzend organisiert. Sie
verfügten über umfangreiches Spruchmaterial und zahlreiches
Personal. Die Mehrzahl der gelösten Tage stammte von ihnen.
Auch in Vignolles wurde fieberhaft gearbeitet. Da es aber
darauf ankam, möglichst viel Spruchmaterial zu lösen und zu
lesen, um es im Generalstab auszuwerten, so saßen denn pol-
nische Kryptologen tagaus tagein an den Enigmen und tasteten
die Sprüche ab oder manipulierten mit den Netzen, um von Zeit
zu Zeit auch einen Tag zu lösen und sich nicht ganz von den
Engländer distanzieren zu lassen. Alles mechanische Arbeiten,
wozu sicherlich Spezialisten nicht nötig waren. So ist es
denn nicht zu verwundern, daß von polnischen Kryptologen
keine wesentlichen Ergebnisse mehr erzielt wurden, sondern,
daß der Schwerpunkt kryptologischer Untersuchungen sich nach
London übertrug.
28. Methode Knox
Der englische Kryptologe Knox hatte bemerkt, daß die deutschen
Schlüssler oft als Grundstellung diejenigen Buchstaben wählten,
die nach Beendigung des Schlüsselns des vorhergehenden Spruches
in den Fenstern der Maschine erscheinen. Besonders häufig trat
dies in vielteiligen Sprüchen auf. Es genügte also in solchen
Fällen von der Grundstellung die Länge des vorhergehenden
Spruches zu subtrahieren, um den Spruchschlüssel des vorherge-
henden Spruches (unverschlüsselt) zu erhalten. Erhielt man
dabei charakteristische Schlüssel wie ASD, WER, OKL, … in
mehreren Teilen eines vielteiligen Spruches, so war man sicher,
daß der Schlüssler einen solchen Fehler begangen hat. Da bei
der Subtraktion der Spruchlänge von der Grundstellung even-
tuelle Drehungen der mittleren und linken Walzen berücksichtigt
werden müssen, so konnte man auf diese Weise teilweise die
Walzenlage bestimmen und dadurch im glücklichen Falle die
Arbeit des Auflösens von 60 auf 3 Walzenlagen herabsetzen.
Wichtig war auch, daß mit Hilfe der Methode Knox die (unver-
schlüsselten) Spruchschlüssel einiger Sprüche bekannt waren.
Diese Methode hatte besonders während des norwegischen Feld-
zuges wertvolle Dienste geleistet, wo Tag auf Tag gelöst wurde,
wobei sich überaus wichtiges und interessantes Material ergab.
29. Kataloge zu den Netzen
Inzwischen verwirklichten die Engländer noch eine Idee pol-
nischer Kryptologen. Es wurde bereits erwähnt, daß das Veri-
fizieren der mittels Netze erhaltenen möglichen Fälle mit
Hilfe des Zyklometers ziemlich zeitraubend war. Mann mußte
jedesmal, wenn ein günstiger Fall vorlag, die Buchstaben,
die den weiblichen Charakter der Position bestimmten, mit
Hilfe des Zyklometers aufsuchen, und mit den Buchstaben der
betreffenden Spruchschlüssel vergleichen. Man trug sich bereits
in Polen mit dem Gedanken, Kataloge herzustellen, die die in
Frage kommenden Buchstaben sämtlicher weiblicher Positionen
enthalten sollten, jedoch technische Schwierigkeiten verhin-
derten die Ausführung dieser Idee. Jetzt wurde sie von den
Engländer mit Hilfe derselben Maschine, die die Netze ange-
fertigt hat, ein weiteres glänzendes Beispiel, wie fruchtbar
sich die polnisch-französisch-englische Zusammenarbeit erwies.
Dank der finanziellen und organisatorischen Möglichkeiten
unseren Londoner Fachgenossen wurden unsere Pläne, die sonst
wohl nie das Licht der Welt erblickt hätten, ohne Rücksicht
auf die Kosten und Schwierigkeiten in Wirklichkeit umgesetzt.
30. Methode Herivel
Ein anderer englischer Kryptologe machte die Entdeckung, daß
einige von deutschen Schlüssler, wenn nach Mitternacht oder
am Morgen die Enigma für betreffenden Tag einstellten, die
Walzen zur Ringstellung nicht herausnahmen und nicht drehten,
und die Grundstellung für den ersten Spruch des Tages die
Buchstaben wählten, die sie in Fenstern der Maschine erblick-
ten. Infolgedessen unterschied sich die Grundstellung dieses
ersten Spruches nicht viel von der für diesen Tag festgestel-
lten Ringstellung.
Durch Vergleich der Grundstellungen von Sprüchen, die von ver-
schiedenen Schlüssler Nachts oder in der frühen Morgenstunden
chiffriert wurden, konnte man oft die Ringstellung genau oder
mit großer Annäherung ausfindig machen. Dank dieser Feststel-
lung wurde die zur Lösung erforderliche Arbeit ganz außeror-
dentlich abgekürzt, so daß oft am frühen Morgen die Engländer
bereits im Besitze des Schlüssels für den ganzen Tag waren.
Zu dieser Methode möge noch folgendes hinzugefügt werden.
Als die Schaltungen der Walzen IV und V gefunden worden,
konnte die Lage des Buchstabenringes für diese Walzen nicht
eindeutig festgestellt werden. Es gab je 26 verschiedene
Lagen, von denen die ersten besten ausgewählt wurden. Man
war sich jedoch darüber im Klaren, daß diese Lagen mit den
originalen Lagen in den Walzen nicht identisch waren. Nach-
dem eine größere Anzahl von Tagen (vor der Entdeckung Herivels)
gelöst war, erinnerte man sich daran, daß früher die drei die
Ringstellung bildenden Buchstaben stets voneinander verschieden
waren. Wenn dieses Merkmal auch jetzt bestehen sollte (was
sehr wahrscheinlich war), es mußten die Lagen der Buchstaben-
ringe in den Walzen IV und V einer gewissen Korrektur unter-
zogen werden. Diese Korrektur wurde gefunden und den Engländern
sofort mitgeteilt. Erst durch diese Korrektur konnte das Ver-
fahren Herivel richtig angewandt werden.
31. Drittes Schlüsselverfahren
Am 1. Mai 1940, vor Beginn der deutschen Offensive gegen Bel-
gien und Holland wurde das Schlüsselverfahren nochmals geän-
dert. Der Spruchschlüssel wurde nicht mehr zweimal, sondern
nur einmal verschlüsselt. Im Kopf des Spruches werden jetzt
sechs Buchstaben angegeben, die drei erste bedeuteten die Grund-
stellung, die drei folgenden den chiffrierten Spruchschlüssel.
Der Sachverhalt wurde dadurch geklärt, daß die deutschen
Schlüssler wieder, wie schon einmal, die Unvorsichtigkeit be-
gingen, bereits am Vorabend der Neueinführung eine Anzahl von
Sprüchen nach dem neuen Verfahren zu schlüsseln. Dieser Tag,
der 30. April 1940, wurde gelöst, nebenbei bemerkt von pol-
nischen Kryptologen, und so stellte sich denn heraus, worauf
das neue Verfahren beruhte.
Es war wieder ein sehr harter Schlag. Die Netze und die Kata-
loge zu den Netzen wurden völlig unbrauchbar, es blieben nur
noch die Methoden Knox und Herivel bestehen. Mit Hilfe dieser
Methoden versuchten die polnische Kryptologen, die vorüberge-
hend von Vignolles nach Paris versetzt waren, wenigstens einen
Tag zu lösen, jedoch vergeblich.
Die Engländer hatten mehr Erfolg. Sie verfügten über bedeutend
umfangreicheres Material, und so gelang es ihnen, nach einer
dreiwöchentlichen Pause wieder einen Tag, den 20. Mai 1940,
zu lösen, und bald darauf fast sämtliche folgenden Tage.
Sie übersandten regelmäßig die Schlüssel, und so saßen wieder
Tag und Nacht die polnischen Spezialisten an den beiden aus
Warschau stammenden Enigmen, um das überaus wertvolle Spruch-
material lesen zu helfen. Nach der Evakuation von Paris wurde
die Arbeit in La Ferté-St. Aubin fortgesetzt, wo ebenfalls
Tag und Nacht gearbeitet wurde und erst unmittelbar vor dem
Waffenstillstand wurde sie abgebrochen. Der letzte Tag, für
die Engländer die Schlüssel übersandten, war der 16. Juni 1940.
folgendermaßen aufschreibt:
(die ersten Zeilen der Substitutionen würden stets lauten
1 2 3 4 … 26)
7 19 3 15 23 11 20 4 16 26 10 14 22 2 17 6 25 9 1 21 12 18 5 24 13 8
16 2 14 22 10 19 3 15 25 9 13 21 1 16 5 24 8 26 20 11 17 4 23 12 7 6
1 13 21 9 18 2 14 24 8 12 20 26 15 4 23 7 25 19 10 16 3 22 11 6 5 17
: :
(das Beispiel ist willkürlich)
Hierauf schreib man auf einem zweiten Bogen mit Öffnungen
(daher der Name Rost) die 6 Substitutionen A1 bis A6 in fol-
gender Form auf:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
V T Z F K D R N O U E W Y H I S X G P B J A L Q M C
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
K Q H U V S Z C O N A T W J I Y B X F L D E M R P G
Nach diesen Vorbereitungen legt man den Rost auf den ersten
Bogen und verschiebt ihn so lange von oben nach unten, bis in
einer bestimmten Lage die in Öffnungen erscheinenden Substi-
tutionen F sämtlich identisch sind. Das trifft natürlich nur
dann ein, wenn keine Steckerverbindungen vorhanden sind. Im
entgegengesetzten Fall ändert sich das Bild, da jedoch die
Steckerverbindungen nicht sämtliche Buchstaben vertauschen,
wird man in einer bestimmten Lage gewisse Analogien zwischen
den 6 verschiedenen Substitutionen F bemerken. Man muß nun
versuchen, die Buchstaben der Substitutionen A1 bis A6 so um-
zustellen, daß alle F identisch werden. Gelingt dies, so er-
geben die Umstellungen der Buchstaben die gesuchten Stecker-
verbindungen, und zugleich erhält man die Position der rechten
Walze sowie die Substitution F.
15. Der Katalog F
Nachdem so die rechte Walze und ihre Position bereits bekannt
war, hätte man die linke und mittlere Walze und ihre Positionen
einfach so bestimmen können, daß man direkt auf der Maschine
sämtliche möglichen Fälle probierte. Um sich jedoch dieselbe
unnütze Arbeit zu ersparen, verfertigte man ein- für allemal
einen Katalog, der sämtliche möglichen Substitutionen F,
deren es
6 · 26 · 26 = 4056
gibt, enthielt. Es genügte jetzt die Substitution F, die man
beim Suchen der Steckerverbindungen erhalten hatte, im Kataloge
nachzuschlagen, um sofort Lage und Stellung der linken und
mittleren Walze zu erfahren.
16. Der Zyklometer
Die Methode, die man anwandte, um die Steckerverbindungen zu
finden, war nicht nur lang und umständlich, sondern sie führte
auch nicht immer zum Ergebnis. Übrigens setzte sie die Kenntnis
des Spruchschlüssel voraus, und die Methoden, diese Schlüssel
zu finden, waren ebenfalls zeitraubend und nicht immer vom
Erfolg gekrönt. So sah man sich denn nach anderen Methoden um,
die schneller und sicherer zum Ziele führen könnten. Man ver-
fiel darauf, daß die Gestalt der Zyklen erstens invariant ge-
genüber den durch die Steckerverbindungen verursachten Substi-
tutionen sei, und zweitens ein Charakteristikum des betref-
fenden Tages bildete, in dem Sinne nämlich, daß zwei Tage deren
Zyklen die gleiche Gestalt hatten, verhältnismäßig selten
vorkommen konnten. So kam man denn auf den Gedanken, die Zyklen
in sämtlichen möglichen Positionen der Walzen, deren es bei
drei Walzen, wie bereits gesagt,
105.456
gab, zu katalogisieren. Um diese Arbeit zu bewältigen, baute
man eine besondere Maschine, den Zyklometer, der aus zwei
Enigmen bestand, die so gekoppelt waren, daß in jeder Position
eine größere oder kleinere Anzahl der Glühlampen gleichzeitig
aufleuchtete, je nach der Länge des entsprechenden Zyklus.
Mehr als ein Jahr verging, ehe die Arbeit beendet war, dann
aber fand man in der Regel schon nach wenigen Minuten Walzen-
lage, Position der Walzen und Steckerverbindungen des betref-
fenden Tages.
17. Grundstellung und Ringstellung
Unter Position der Walzen verstehen wir stets die Differenz
zwischen Grund- und Ringstellung. Um also den völligen Besitz
des Tagesschlüssels zu gelangen, mussten noch die beiden letzten
Elemente des Tagesschlüssels, d.h. Grund- und Ringstellung
gefunden werden. Dazu genügt es offenbar nicht, sich auf das
Studium der Spruchschlüssel zu beschränken, vielmehr muß auf
den Inhalt der Sprüche zurückgegriffen werden.
Als man das Material von Oktober und Dezember 1931, für das
Schlüssel vorhanden war, löste, bemerkte man, daß der Text
sehr vieler Sprüche mit Buchstaben AN begann.
Um also Grund- und Ringstellung gesondert zu erhalten, nahm
man irgendeinen Spruch, von dem man vermutete, daß er mit
Buchstaben AN begann und probierte in sämtlichen Positionen
der Maschine, ob diese Annahme möglich ist. Eine langwierige
Arbeit, wenn man bedenkt, daß dabei 263 = 17.576 Positionen
untersucht werden müssen.
Später überzeugte man sich, daß, wenn ein Spruch mit den Buch-
staben AN begann, a priori gewisse Positionen der rechten Walze
unmöglich waren. Und da man täglich über eine ganze Anzahl von
Sprüchen verfügte, in denen man ein AN am Anfang erhofft durfte,
so gelang es meistens rein rechnerisch die richtige Position
der rechten Walze zu erhalten.
18. Einige Bemerkungen
Bei der Beschreibung des Rostes und des Zyklometers wurde vor-
ausgesetzt, daß während des Schlüsselns des Spruchschlüssels
die mittlere Walze sich nicht drehte. In Wirklichkeit ist
diese Voraussetzung nicht bedingt erforderlich, ja die Auf-
findung von Grund- und Ringstellung ist sogar besonders leicht
gerade dann, wenn eine Drehung der mittleren Walze eintritt.
Wir überlassen es dem Leser zu ermitteln, wie sich in solchen
Fällen die Verhältnisse gestalten.
Man hat bemerkt, daß innerhalb eines Tages die sechs Grund
und Ringstellung bildenden Zahlen bzw. Buchstaben stets von-
einander verschieden waren. Diese Feststellung führte nicht
nur in gewissen Fällen zu bedeutender Vereinfachung der Arbeit,
sondern sie erlaubte es auch in späteren Jahren die Methode
Herivel, von der noch die Rede sein wird, zweckmäßig anzu-
wenden. Es gab übrigens auch Zeiträume, wo gar stets in vier
aufeinander folgenden Tagen alle 24, die Grund- und Ringstel-
lungen bildenden Zahlen bzw. Buchstaben voneinander verschie-
den waren.
Ähnliche Entdeckungen hat man zu verschiedenen Zeiten auch
mit den Steckerverbindungen gemacht.
19. Neue Netze. Beständige Änderungen
Im Maße wie sich die deutsche Wehrmacht entwickelte, wurde
auch die Zahl der Heeresfunkstellen immer mehr vergrössert.
Dabei wurde allmählich ebenfalls die Zahl der Funknetze, die
sich alle derselben Enigma, jedoch mit anderen Tagesschlüssel
bedienten, vermehrt. So bildete z.B. die neugegründete deu-
tsche Luftflotte mit dem 1. August 1935 ihr eigenes Funknetz
mit eigenem Tagesschlüssel.
Um die Unauflösbarkeit des Enigmaverfahrens sicherzustellen,
wurden verschiedene Neuerungen eingeführt. Ab 1. Februar 1936
wurde die Walzenlage monatlich, und ab 1. Oktober 1936 sogar
täglich geändert. Gleichzeitig wurde die Zahl der Steckerver-
bindungen geändert, sie betrug nicht mehr als 6, wie bisher,
sondern 5 bis 8. Und schließlich wurde noch am 2. November 1937
die bisherige Umkehrwalze aus dem Verkehr genommen und durch
eine neue, die sogenannte Umkehrwalze B, ersetzt.
20. Umkehrwalze B
Von Seiten der deutschen Schlüssler wurde die Unvorsichtigkeit
begangen, in den Funksprüchen vom September 1937 von der be-
vorstehenden Änderung der Umkehrwalze zu reden. So war man denn
in der polnischen Schlüsselstelle auf die Änderung vorbereitet
und wunderte sich nicht, als die Gestalt der Zyklen vom 2. No-
vember 1937 im Kataloge nicht aufzufinden war. Dagegen konnte
man natürlich nach wie vor mit Hilfe des Rostes die Stecker-
verbindungen sowie die rechte Walze und ihre Position bestimmen.
Unbekannt blieben nur die linke und mittlere Walze sowie ihre
Positionen. Das ergab 2 · 26 · 26 = 1352 mögliche Fälle und
jeder dieser Fälle bestimmte eine Umkehrwalze. Durch Vergleich
dieser 1352 Umkehrwalzen in zwei verschiedenen Tagen konnte
leicht die richtige Umkehrwalze ermittelt werden.
21. Neue Chiffrierwalzen
Im September 1937 bildete sich ein neues Funknetz, nämlich
das Funknetz des Sicherheitsdienstes, einer politischen Orga-
nisation, von der noch später die Rede sein wird. Das Schlüs-
selverfahren war in diesem Netze im Großen und Ganzen dasselbe,
wie in der Armee, jedoch wurden gewisse Neuerungen nicht gleich-
zeitig, sondern mit einer bestimmten Verspätung eingeführt.
So z.B. wurde am 15. September 1938 das Schlüsselverfahren im
Heere und in der Luftwaffe vollständig umgeschaltet, dagegen
blieb es im Sicherheitsdienst noch mehrere Monate lang unver-
ändert, ein grober Fehler, der sich sofort rächen sollte.
Denn bereits drei Monate später wurden, diesmal gleichzeitig
in allen Netzen, zwei neue Chiffrierwalzen, die Walzen IV und
V eingeführt. Da in diesem Augenblicke das Netz des Sicher-
heitsdienstes sich noch des alten Verfahrens bediente, kon-
nten die Schaltungen dieser Walzen in ähnlicher Weise gefunden
werden, wie die Schaltungen der Umkehrwalze B. Es erübrigt
sich wohl, in Einzelheiten einzugehen, es möge nur angedeutet
werden, daß man sich hierbei zweier Tage, in denen Drehung
der mittleren Walze eintrat, bediente. Wäre im Sicherheits-
dienst das neue Chiffrierverfahren früher eingeführt worden,
so hätte man wohl kaum die Schaltungen der Walzen IV und V
auf kryptologischem Wege erhalten.
22. Änderung des Chiffriersystems
Dank der beschriebenen Methoden konnten bis September 1938
tagtäglich sämtliche Netze d.h. Heer, Luftwaffe, Sicherheits-
dienst, Marine (von der noch weiter unten die Rede sein wird)
in oft unglaublich kurzer Zeit gelöst werden.
Die Sachlage änderte sich jedoch vollkommen, als am 15. Sep-
tember 1938 ein neues Chiffrierverfahren eingeführt wurde und
hierdurch die bisherigen Errungenschaften polnischer Krypto-
logen auf diesem Gebiete ernsthaft bedroht wurden.
Das neue Schlüsselverfahren beruhte darauf, daß die Grundstel-
lung nicht mehr eine und dieselbe war für sämtliche Sprüche
eines Tages, sondern von Spruch zu Spruch wechselte.
Wir wollen das neue Schlüsselverfahren an einem Beispiele er-
läutern. Der Schlüssler wählt sich zwei Buchstabentripel, z.B.
SKR WTC, stellt die Maschine auf SKR ein und schlüsselt die
Buchstaben WTC zweimal hintereinander (wie bisher), wobei
etwa die sechs Buchstaben KFDLSF erhalten möge.
Die Grundstellung SKR wird unverschlüsselt in den Kopf des
Spruches, die sechs Buchstaben KFD LSF am Anfang des Spruches
eingesetzt, und der Spruch selbst wird von der Stellung WTC
aus verschlüsselt (also so wie bisher). Daß das neue Verfahren
gerade so, wie beschrieben, und nicht anders war, erfuhr man
dadurch, daß bereits am Vortage der Systemänderung einige
Schlüssler sich des neuen Verfahrens bedienten, was natür-
lich ein grober Fehler war.
23. Auffindung der Walzenlage
Da bei dem neuen System die Spruchschlüssel nicht mehr von
ein- und derselben Position aus verschlüsselt werden, so wurde
die Zyklentheorie und die darauf aufgebauten Methoden der
Spruchschlüssels, des Rostes und des Zyklometers hinfällig.
Man ließ jedoch die Arme nicht hängen, sondern schritt zur
Untersuchung des neuen Verfahrens. Als erstes stellte man fest,
daß wenn das Spruchmaterial innerhalb eines Tages und eines
Netzes genügend umfangreich war, man von Zeit zu Zeit auf
Paare von Grundstellungen traf, deren erste und zweite Buch-
stabe identisch, und deren dritte Buchstaben im Alphabet neben-
einander oder fast nebeneinander standen, wie etwa TKP und TKR.
Wenn dann zufälligerweise auch in den Spruchschlüsseln gleiche
Buchstaben an entsprechenden Stellen auftraten, so konnte man
hieraus bisweilen schlußfolgern, welche Walzen sich rechts oder
in der Mitte befinden. Wir wollen die verschiedenen Möglichkei-
ten an einigen Beispiele klarmachen.
1) Angenommen, wir hätten zwei Sprüche mit folgenden Schlüsseln
gefunden:
Grundstellung Spruchschlüssel
TKP ANV CKB
TKR VTS JQM
In diesem Fall ist sicher, daß zwischen Buchstaben P und R
eine Drehung der mittleren Walze stattfindet, d.h. daß rechts
sich die Walze I befindet, da diese und nur diese eine Drehung
zwischen Q und R hervorruft. Im entgegengesetzten Falle würden
den gleichen Buchstaben V auch gleiche Buchstaben B (oder J)
entsprechen.
2) Grundstellung Spruchschlüssel
TKP ANV CKB
TKR VTS BQM
In diesem Falle ist es wenig wahrscheinlich, daß eine Drehung
zwischen P und R eintritt, daß also rechts sich die Walze I
befindet.
3) Auch Grundstellungen mit verschiedenen mittleren Buchstaben
können Aufschlüsse über die Walzenlage bieten, wie folgendes
Beispiel zeigt:
Grundstellung Spruchstellung
TKP ANV CKB
TLR VTS JQM
Zwischen P und R kann keine Verschiebung der mittleren Walze
eintreten, also ist die rechte Walze sicher verschieden von
der Walze I.
4) Ja sogar aus Grundstellungen mit verschiedenen ersten Buch-
staben lassen sich bisweilen Schlüsse über Walzenlage ziehen.
Grundstellung Spruchschlüssel
TJG CES PKR
UKG CNT PLJ
In diesem Falle ist es wahrscheinlich, daß zwischen J und K
sich die linke Walze gedreht hat, daß also in der Mitte sich
die Walze IV befindet. In anderen Fällen lassen sich ähnliche
Schlüsse ziehen.
24. Bomben
Bereits wenige Tage nach Einführung des neuen Schlüsselverfah-
rens hatte man einen Plan gefaßt, wie man die entstandenen
Schwierigkeiten aus dem Wege schaffen könnte. Unser Ideengang
war folgender:
Nehmen wir eine Anzahl von Sprüchen und schreiben deren Grund-
stellungen und Spruchschlüssel auf.
1. KTL WOC DRB 7. GRA FDR YWD
2. SVW KKM IYS 8. MDO OTW YZW
3. JOT IWA BWN 9. KJC FSW RSE
4. EDC DSP LJC 10. SGF TEY ASR
5. GDK WAV WHA 11. AGH MDF RHF
6. BWK TCA TOC 12. JBR WLT SOQ
Richten wir jetzt unsere Aufmerksamkeit auf den Spruch Nr. 3.
In dessen Spruchschlüssel kommt der Buchstabe W zweimal im Ab-
stande von 3 Buchstaben vor. Das bedeutet, daß in einer ganz
bestimmten Position der Maschine der Buchstabe W einen uns un-
bekannten Buchstaben, sagen wir etwa X, ergeben und drei Po-
sitionen später derselbe Buchstabe W wieder denselben Buch-
stabe X ergeben würde. Nehmen wir nun noch an, der Buchstabe W
werde durch Steckerverbindungen nicht berührt, eine Annahme,
die bei 5 bis 8 Steckerverbindungen in 50% aller Fälle zutref-
fend ist.
Dann könnte man die richtige Position der Walzen ermitteln,
daß in zwei Maschinen, deren Positionen sich um 3 unterschei-
den, der Buchstabe W gleichzeitig getastet und daraufhin in
beiden Maschinen die Walzen synchronisch gedreht werden. Jedes-
mal, wenn in beiden Maschinen gleichzeitig derselbe Buchstabe
aufleuchtet, haben wir es mit einem Fall zu tun, der möglicher-
weise richtig ist und daher besonders untersucht werden muss.
Da jedoch solche Fälle allzu häufig auftreten würden, hilft
man sich in der Weise, daß man nicht einen, sondern drei Sprü-
che, in deren Spruchschlüssel der Buchstabe W zweimal im Ab-
stande von 3 Buchstaben vorkommt, benutzt. In unserem Beispiel
wären es Sprüche Nr. 3, 5 und 8. Nur muß man sich natürlich
nicht zweier, sondern sechs Maschinen bedienen. Es wäre aber
in Wirklichkeit höchst umständlich und unzweckmäßig, wollte
man wirklich mit sechs einzelnen Maschinen manipulieren. Viel-
mehr man eine Maschine, Bombe genannt, die 6 Enigmen entsprach,
elektrisch angetrieben wurde und jedesmal automatisch anhielt,
wenn ein günstiger Fall vorlag. Es wurden in der polnischen
Schlüsselstelle sechs solche Bomben montiert, für jede Walzen-
lage eine (denn die Walzen IV und V wurden erst später einge-
führt), wobei jede Bombe alle möglichen 17.576 Fälle in 1,5
Stunden bewältigte.
25. Die Netze
Die Bomben befanden sich noch im Bau, als bereits neue Ände-
rungen eintraten. Am 15. Dezember 1938 wurden die Walzen IV
und V eingeführt, die Anzahl der möglichen Walzenlagen also
verzehnfacht, und zwei Wochen später die Zahl der Steckerver-
bindungen auf 7 - 10 erhöht. Durch diese Änderungen verloren
die Bomben praktisch den größten Teil ihrer Bedeutung, da
die Lösung eines Tages zu viel Zeit beanspruchen würde. Es
gelang zwar bisweilen, dank der früher angegebenen Methode
die Walzenlage teilweise zu bestimmen, aber nur dann, wenn
umfangreiches Material vorhanden war, was verhältnismäßig
selten eintrat. Auch war die Anwendbarkeit der Bomben durch
die Steckerverbindungen eingeschränkt.
Man schuf daher bereits sehr früh eine neue Methode, die von
der Zahl der Steckerverbindungen unabhängig war.
Zur Darlegung dieser neuen Methode müssen wir zunächst einen
neuen Begriff, den der männlichen und weiblichen Positionen,
einführen. Kehren wir noch einmal zu den Sprüche zurück:
1. KTL WOC DRB 7. GRA FDR YWD
2. SVW KKM IYS 8. MDO OTW YZW
3. JOT IWA BWN 9. KJC FSW RSE
4. EDC DSP LJC 10. SGF TEY ASR
5. GDK WAV WHA 11. AGH MDF RHF
6. BWK TCA TOC 12. JBR WLT SOQ
Ein Fall, wie im Spruchschlüssel Nr. 3, daß derselbe Buchstabe
(in unserem Beispiel W) zweimal im Abstand von drei Buchstaben
vorkommt, kann nicht in sämtlichen Positionen der Maschine
eintreten. Vielmehr haben Rechnungen ergeben, daß solche Fäl-
le in etwa 40% aller Positionen eintreten (genau genommen be-
trägt das Verhältnis 1 - (1/√e), wobei e die Basis der
natürlichen Logarithmen ist). Diese Positionen nennen wir
weibliche Positionen, die übrigen heißen männliche Positionen.
In unserem Beispiel gehören die sechs Sprüche Nr. 3, 5, 6, 8,
9, 11 bestimmt weiblichen Positionen an, während von den
übrigen Sprüchen nichts ausgesagt werden kann. Die Stecker-
verbindungen haben natürlich Einfluß auf die in den Spruch-
schlüsseln auftretenden Buchstaben, nicht aber auf das Ge-
schlecht der Position (ob weiblich oder männlich).
Man konnte daher einen Katalog mit sämtlichen weiblichen Po-
sitionen anfertigen, und in diesem Kataloge nachsuchen, ob
man nicht sechs weibliche Positionen findet, die in denselben
Abständen auftreten, wie die Grundstellungen: JOU, GKD, BWK,
MDR, KJD, AGK (dabei müssen auch eventuell Drehungen der mit-
tleren wie auch linken Walze berücksichtigt werden).
Da dies jedoch praktisch unausführbar wäre, so ging man anders
vor; man stellte die sogenannte Netze her: Für jede Walzenlage
werden sämtliche weibliche Positionen auf 26 Bogen Papier,
von denen jeder 26x26 Felder, und zwar in vierfacher Ausfüh-
rung enthält, eingetragen. Die verschiedenen Bogen entsprechen
den 26 Positionen der linken Chiffrierwalze, die 26x26 Felder
der mittleren und rechten Walze. Der Grund der vierfachen Aus-
führung wird unten erklärt werden. Die Felder die den weib-
lichen Positionen entsprechen, werden durchlocht (daher der
Name Netz).
Nun werden, um auf unseres Beispiel zurückzugehen, sechs von
den 26 Bogen in einer Reihenfolge und in einer Lage, die den
gegenseitigen Entfernungen der Grundstellungen entspricht,
aufeinander gelegt. Wenn gleichzeitig in allen sechs Bogen an
derselben Stelle ein Loch erscheint, so haben wir es mit einem
möglicherweise richtigen Falle zu tun, der besonders geprüft
werden muß. Um alle möglichen Fälle zu erschöpfen, müssen die
Bogen der Reihe nach zyklisch vertauscht werden. Auf jedem
Bogen befinden sich die 26x26 Felder in vierfacher Ausführung,
weil die Bogen nicht direkt, sondern gegenseitig verschoben
aufeinander gelegt werden. Die Erzielung des Ergebnisses ist
von einem überaus sorgfältigen Aufeinanderlegen der Bogen in
der richtigen Lage abhängig. Deshalb wurde stets vor Beginn
der Arbeit auf einem besonderen Zettel, dem sogenanntem Menu,
die Reihenfolge und gegenseitige Lage der Bogen festgelegt.
Die Kenntnis, welche Positionen weiblich und welche männlich
sind, wurde den Katalogen zum Zyklometer entnommen, denn offen-
bar entsprechende weibliche Positionen denjenigen Substitutionen,
in denen Zyklen vorkommen, die aus einem Buchstabe bestehen.
Das Prüfen der richtigen Fälle geschah auch mit Hilfe des
Zyklometers. Da dies ziemlich zeitraubend war, trug man sich
mit dem Gedanken, besondere Kataloge herzustellen, in denen
nicht nur die weibliche Positionen, sondern auch alle Buch-
staben, die in den eingliedrigen Zyklen vorkommen, eingetragen
wären. Aber dieser Gedanke wurde erst später, und zwar von der
englischen Schlüsselstelle, verwirklicht.
26. Die Warschauer Konferenz
In der Polnischen Schlüsselstelle wurden zwei Sätze von je 26
Netzen für zwei Walzenlagen mit der Hand angefertigt, und man
überzeugte sich daß die Idee der Netze vollkommen brauchbar
ist. Ganz anders jedoch stellte sich die Ausführung dieser
Idee dar.
Während die weiblichen Positionen für die Walzenlagen I II III,
I III II, …, III II I direkt von den Katalogen entnommen wer-
den konnten, müßte man für die übrigen 54 Walzenlagen die
weibliche Positionen erst ermitteln, entweder mittels des Zy-
klometers, was mehrere Jahre beansprucht hätte, oder mit Hilfe
einer neuen kostspieligen Maschine, woran man zunächst noch
nicht denken wollte. Ferner war das handmäßige Perforieren
bereits der beiden ersten Sätze von je 26 Netzen recht mühsam
gewesen, so daß man für den Rest der Arbeit ebenfalls beson-
dere Apparate benötigt haben wäre. Und schließlich wäre, wenn
schon alles fertig wäre, das Manipulieren mit den 60 Sätzen
von Netzen, um die einzelnen Tage zu lösen, ein zahlreiches
Hilfspersonal erfordern.
Da die polnische Schlüsselstelle nicht in der Lage war, all
diese Schwierigkeiten selbst zu bewältigen, entschloss man
sich, das Geheimnis der Enigma, das bisher sorgsam gehütet
war, auch der französischen und englischen Schlüsselstellen
anzuvertrauen.
Am 26. Juli trat in Warschau eine dreitägige Konferenz unter
Teilnahme von Vertretern der französischen und englischen
Schlüsselstelle in Sachen der Enigma zusammen. Es stellte
sich heraus, daß weder unsere französischen noch englischen
Fachgenossen die ersten Schwierigkeiten haben überwinden
können. Die Walzenschaltungen waren ihnen unbekannt, mithin
auch etwaige Auflösungsmethoden. Wir legten ihnen die Ergeb-
nisse unserer siebenjährigen Arbeit, sowie die Schwierigkeiten,
auf die wir zuletzt gestoßen waren, vor. Von Seiten der En-
gländer wurde bereitwilligst Hilfe in der Ausführung der Netze
für die 60 Walzenlagen versprochen.
27. Kriegsaufbruch. Vignolles
Ein Monat später brach der deutsch-polnische Krieg aus. Es ge-
lang noch, den 25. August 1939, den Tag der allgemeinen Mobil-
machung in Deutschland, zu lösen, als bereit die Evakuierung
begann. Die Bomben, Zyklometer, Enigmen, Netze, sämtliche Akten
und Aufzeichnungen wurden mitgenommen, aber auf dem Wege zur
rumänischen Grenze vernichtet. Einzig und allein zwei Enigmen
wurden gerettet. In Bukarest nahm sich der drei Spezialisten
von der Enigma die französische Botschaft an und schickte sie
sofort nach Paris, wo sie gastfreundlich aufgenommen wurden.
Einige Wochen später schuf der französische Generalstab in
Vignolles, einem Schlößchen unweit Gretz, 30 km von der Haupt-
stadt entfernt, ein Büro, wo polnische Kryptologen samt Hilfs-
personal unter Leitung von Oberstleutnant Langer versuchten,
die in Polen unterbrochene Arbeit wiederaufzunehmen. Man be-
gann wieder mühselig, wie bereits schon einmal in Warschau,
die Netze mit der Hand zu fabrizieren, eine Arbeit, die wohl
erst nach Jahren beendet worden wäre.
Jetzt aber begann die Warschauer Konferenz Früchte zu tragen.
Es stellte sich heraus, daß in der Zwischenzeit die Engländer
eine Maschine konstruiert hatten, die ihnen ermöglichte, die
Netze für sämtliche 60 Walzenlagen in wenigen Wochen herzu-
stellen. Aber Proben, die mit diesen Netzen in England ange-
stellt wurden, gaben kein Ergebnis. Da glücklicherweise die
Netze in zwei Exemplaren hergestellt waren, konnten uns die
Engländer ein Exemplar zur Verfügung stellen, was sie auch
freundlichst taten. Sobald diese Netze in Vignolles ankamen,
begann eine angestrengte Arbeit, und bald waren zwei Tage,
der 28.10.1939 und der 6.1.1940 gelöst werden würde.
Die Engländer haben ihre Arbeit glänzend organisiert. Sie
verfügten über umfangreiches Spruchmaterial und zahlreiches
Personal. Die Mehrzahl der gelösten Tage stammte von ihnen.
Auch in Vignolles wurde fieberhaft gearbeitet. Da es aber
darauf ankam, möglichst viel Spruchmaterial zu lösen und zu
lesen, um es im Generalstab auszuwerten, so saßen denn pol-
nische Kryptologen tagaus tagein an den Enigmen und tasteten
die Sprüche ab oder manipulierten mit den Netzen, um von Zeit
zu Zeit auch einen Tag zu lösen und sich nicht ganz von den
Engländer distanzieren zu lassen. Alles mechanische Arbeiten,
wozu sicherlich Spezialisten nicht nötig waren. So ist es
denn nicht zu verwundern, daß von polnischen Kryptologen
keine wesentlichen Ergebnisse mehr erzielt wurden, sondern,
daß der Schwerpunkt kryptologischer Untersuchungen sich nach
London übertrug.
28. Methode Knox
Der englische Kryptologe Knox hatte bemerkt, daß die deutschen
Schlüssler oft als Grundstellung diejenigen Buchstaben wählten,
die nach Beendigung des Schlüsselns des vorhergehenden Spruches
in den Fenstern der Maschine erscheinen. Besonders häufig trat
dies in vielteiligen Sprüchen auf. Es genügte also in solchen
Fällen von der Grundstellung die Länge des vorhergehenden
Spruches zu subtrahieren, um den Spruchschlüssel des vorherge-
henden Spruches (unverschlüsselt) zu erhalten. Erhielt man
dabei charakteristische Schlüssel wie ASD, WER, OKL, … in
mehreren Teilen eines vielteiligen Spruches, so war man sicher,
daß der Schlüssler einen solchen Fehler begangen hat. Da bei
der Subtraktion der Spruchlänge von der Grundstellung even-
tuelle Drehungen der mittleren und linken Walzen berücksichtigt
werden müssen, so konnte man auf diese Weise teilweise die
Walzenlage bestimmen und dadurch im glücklichen Falle die
Arbeit des Auflösens von 60 auf 3 Walzenlagen herabsetzen.
Wichtig war auch, daß mit Hilfe der Methode Knox die (unver-
schlüsselten) Spruchschlüssel einiger Sprüche bekannt waren.
Diese Methode hatte besonders während des norwegischen Feld-
zuges wertvolle Dienste geleistet, wo Tag auf Tag gelöst wurde,
wobei sich überaus wichtiges und interessantes Material ergab.
29. Kataloge zu den Netzen
Inzwischen verwirklichten die Engländer noch eine Idee pol-
nischer Kryptologen. Es wurde bereits erwähnt, daß das Veri-
fizieren der mittels Netze erhaltenen möglichen Fälle mit
Hilfe des Zyklometers ziemlich zeitraubend war. Mann mußte
jedesmal, wenn ein günstiger Fall vorlag, die Buchstaben,
die den weiblichen Charakter der Position bestimmten, mit
Hilfe des Zyklometers aufsuchen, und mit den Buchstaben der
betreffenden Spruchschlüssel vergleichen. Man trug sich bereits
in Polen mit dem Gedanken, Kataloge herzustellen, die die in
Frage kommenden Buchstaben sämtlicher weiblicher Positionen
enthalten sollten, jedoch technische Schwierigkeiten verhin-
derten die Ausführung dieser Idee. Jetzt wurde sie von den
Engländer mit Hilfe derselben Maschine, die die Netze ange-
fertigt hat, ein weiteres glänzendes Beispiel, wie fruchtbar
sich die polnisch-französisch-englische Zusammenarbeit erwies.
Dank der finanziellen und organisatorischen Möglichkeiten
unseren Londoner Fachgenossen wurden unsere Pläne, die sonst
wohl nie das Licht der Welt erblickt hätten, ohne Rücksicht
auf die Kosten und Schwierigkeiten in Wirklichkeit umgesetzt.
30. Methode Herivel
Ein anderer englischer Kryptologe machte die Entdeckung, daß
einige von deutschen Schlüssler, wenn nach Mitternacht oder
am Morgen die Enigma für betreffenden Tag einstellten, die
Walzen zur Ringstellung nicht herausnahmen und nicht drehten,
und die Grundstellung für den ersten Spruch des Tages die
Buchstaben wählten, die sie in Fenstern der Maschine erblick-
ten. Infolgedessen unterschied sich die Grundstellung dieses
ersten Spruches nicht viel von der für diesen Tag festgestel-
lten Ringstellung.
Durch Vergleich der Grundstellungen von Sprüchen, die von ver-
schiedenen Schlüssler Nachts oder in der frühen Morgenstunden
chiffriert wurden, konnte man oft die Ringstellung genau oder
mit großer Annäherung ausfindig machen. Dank dieser Feststel-
lung wurde die zur Lösung erforderliche Arbeit ganz außeror-
dentlich abgekürzt, so daß oft am frühen Morgen die Engländer
bereits im Besitze des Schlüssels für den ganzen Tag waren.
Zu dieser Methode möge noch folgendes hinzugefügt werden.
Als die Schaltungen der Walzen IV und V gefunden worden,
konnte die Lage des Buchstabenringes für diese Walzen nicht
eindeutig festgestellt werden. Es gab je 26 verschiedene
Lagen, von denen die ersten besten ausgewählt wurden. Man
war sich jedoch darüber im Klaren, daß diese Lagen mit den
originalen Lagen in den Walzen nicht identisch waren. Nach-
dem eine größere Anzahl von Tagen (vor der Entdeckung Herivels)
gelöst war, erinnerte man sich daran, daß früher die drei die
Ringstellung bildenden Buchstaben stets voneinander verschieden
waren. Wenn dieses Merkmal auch jetzt bestehen sollte (was
sehr wahrscheinlich war), es mußten die Lagen der Buchstaben-
ringe in den Walzen IV und V einer gewissen Korrektur unter-
zogen werden. Diese Korrektur wurde gefunden und den Engländern
sofort mitgeteilt. Erst durch diese Korrektur konnte das Ver-
fahren Herivel richtig angewandt werden.
31. Drittes Schlüsselverfahren
Am 1. Mai 1940, vor Beginn der deutschen Offensive gegen Bel-
gien und Holland wurde das Schlüsselverfahren nochmals geän-
dert. Der Spruchschlüssel wurde nicht mehr zweimal, sondern
nur einmal verschlüsselt. Im Kopf des Spruches werden jetzt
sechs Buchstaben angegeben, die drei erste bedeuteten die Grund-
stellung, die drei folgenden den chiffrierten Spruchschlüssel.
Der Sachverhalt wurde dadurch geklärt, daß die deutschen
Schlüssler wieder, wie schon einmal, die Unvorsichtigkeit be-
gingen, bereits am Vorabend der Neueinführung eine Anzahl von
Sprüchen nach dem neuen Verfahren zu schlüsseln. Dieser Tag,
der 30. April 1940, wurde gelöst, nebenbei bemerkt von pol-
nischen Kryptologen, und so stellte sich denn heraus, worauf
das neue Verfahren beruhte.
Es war wieder ein sehr harter Schlag. Die Netze und die Kata-
loge zu den Netzen wurden völlig unbrauchbar, es blieben nur
noch die Methoden Knox und Herivel bestehen. Mit Hilfe dieser
Methoden versuchten die polnische Kryptologen, die vorüberge-
hend von Vignolles nach Paris versetzt waren, wenigstens einen
Tag zu lösen, jedoch vergeblich.
Die Engländer hatten mehr Erfolg. Sie verfügten über bedeutend
umfangreicheres Material, und so gelang es ihnen, nach einer
dreiwöchentlichen Pause wieder einen Tag, den 20. Mai 1940,
zu lösen, und bald darauf fast sämtliche folgenden Tage.
Sie übersandten regelmäßig die Schlüssel, und so saßen wieder
Tag und Nacht die polnischen Spezialisten an den beiden aus
Warschau stammenden Enigmen, um das überaus wertvolle Spruch-
material lesen zu helfen. Nach der Evakuation von Paris wurde
die Arbeit in La Ferté-St. Aubin fortgesetzt, wo ebenfalls
Tag und Nacht gearbeitet wurde und erst unmittelbar vor dem
Waffenstillstand wurde sie abgebrochen. Der letzte Tag, für
die Engländer die Schlüssel übersandten, war der 16. Juni 1940.
| 32. Chronologische Übersicht über die Änderungen des Schlüsselverfahrens im Heer und in der Luftwaffe |
|---|
| 15. Jul. | 1928 | Enigma G mit Stöpselstellung |
| 1929 |
| 31. Mai | 1930 | |
| 01. Jun. | 1930 | *1 | Walzenlage | Stecker- | *2 | *4 | Erstes Schlüssel- |
| 1931 | ändert | verbindung | verfahren. |
| 1932 | sich | tauschen | Grundstellung |
| 1933 | alle | sechs | dieselbe für alle |
| 1934 | drei | Paar | Sprüche. |
| 1935 | Monate | Buchstaben | Spruchschlüssel |
| 31. Jan. | 1936 | | | zweimal |
| 01. Feb. | 1936 | Walzenlage ändert | Stecker- | verschlüsselt. |
| 30. Sep. | 1936 | sich jeden Monat | verbindungen | |
| 01. Okt. | 1936 | Walzenlage | tauschen |
| 01. Nov. | 1937 | ändert | 5 - 8 |
| 02. Nov. | 1937 | sich | Paar | *3 |
| 14. Sep. | 1938 | täglich | Buchstaben |
| 15. Sep. | 1938 | | | Zweites Schlüssel- |
| 14. Dez. | 1938 | verfahren. |
| 15. Dez. | 1938 | *5 | Grundstellung |
| 31. Dez. | 1938 | wechselt von |
| 01. Jan. | 1939 | Steckerverbindungen tauschen | Spruch zu Spruch. |
| 31. Dez. | 1939 | 7 - 10 Paar Buchstaben | Spruchschlüssel |
| 01. Jan. | 1940 | Steckerverbindungen | zweimal verschlüsselt. |
| 30. Apr. | 1940 | tauschen zehn Paar | |
| 01. Mai | 1940 | Buchstaben | *6 |
| *1 | Enigma M mit Steckerbrettverbindungen |
| *2 | Umkehrwalze A |
| *3 | Umkehrwalze B |
| *4 | Walzen I - III |
| *5 | Walzen IV - V |
| *6 | Drittes Schlüsselverfahren. Grundstellung wechselt von Spruch zu Spruch. |
| Spruchschlüssel einmal verschlüsselt. |
33. Das Funknetz des Sicherheitsdienstes
Das Funknetz des Sicherheitsdienstes wurde bereits erwähnt.
Da dieses Netz, abgekürzt S.D. genannt, sich eines Schlüs-
selverfahrens bedient, daß in Einzelheiten von demjenigen des
Heeres und der Luftwaffe abwich, so möge es hier etwas genauer
beschrieben werden.
Bis 1. August 1939 bestand der Hauptunterschied zwischen dem
Verfahren S.D. und den übrigen Verfahren darin, daß der Text
der Sprüche mit dreistelligen Satzbuchgruppen vermischt war.
Das Satzbuch diente anscheinend vor allem dazu, den Inhalt
der Sprüche abzukürzen. Es war nicht besonders schwer, dieses
Satzbuch zu lösen, doch wurde es alle paar Monate geändert
und durch ein umfangreicheres ersetzt, so daß man die Arbeit
stets aufs Neue beginnen mußte.
Der Spruchschlüssel wurde wie im Heer und in der Luftflotte
zweimal verschlüsselt, doch wurde er nicht immer an Anfang,
sondern bisweilen auch an anderen Stellen eingesetzt. Außer-
dem wurden während der Dauer von mehreren Monaten die Buch-
staben der Spruchschlüssel noch mittels eines Tauschalphabets
überschlüsselt. Die Gültigkeit eines Tauschalphabets betrug
jeweils einen Monat.
Die Spruchschlüssel wurden sehr sorgfältig gewählt, so daß
nur die Methode ungleicher Buchstaben und der Zyklometer an-
gewandt werden konnten.
Sprüche, die mit den Buchstaben AN begannen, kamen nicht vor.
Um also Grund- und Ringstellung gesondert zu finden, mußte
man von anderen charakteristischen Eigenschaften des Spruchin-
halts ausgehen. Es stellte sich heraus, daß in sehr vielen
Sprüche der vierte und fünfte oder der fünfte und sechste
Buchstabe QY lautete, und man also mit diesen Buchstaben ebenso
vorgehen konnte, wie im Heer mit den Buchstaben AN.
Ihrem Inhalt nach waren die Sprüche von großer Wichtigkeit.
Es waren sehr oft Berichte von außerhalb Deutschland sich be-
findenden Agenten des Sicherheitsdienstes, und man konnte
sich mit ihrer Hilfe ein Bild über die weit verzweigte Orga-
nisation des deutschen Spionagedienstes machen.
Das am 15. September 1938 im Heer und in der Luftflotte ein-
geführte zweite Schlüsselverfahren wurde im S.D. Netz nicht
beachtet. Es wurde nach wie vor nach dem alten System geschlüs-
selt, nur wurde durch Einsetzen in den Kopf der Sprüche einer
dreistelligen Buchstabengruppe das neue System vorgetäuscht.
Dagegen trat am 1. August 1939 eine völlige Änderung des Ver-
fahrens ein, daß man nicht enträtseln konnte. Seit dieser Zeit
blieben die Sprüche des S.D. Netzes unauflösbar. Der letzte
gelöste Tag war der 31. Juni 1939.
Aus Mangel an Unterlagen kann eine chronologische Zusammen-
stellung der in S.D. Funknetz eingetretenen Veränderungen der
verschiedenen Schlüsselmittel wie Satzbücher, Tauschalphabete,
Einsatzstellen für Spruchschlüssel, usw. nicht angegeben werden.
34. Die Schlüsselverfahren der deutschen Kriegsmarine vor
Einführung der Enigma
Die Schlüsselverfahren, die Deutsche Kriegsmarine anwandte,
unterschieden sich, obwohl seit dem Jahre 1934 auch dort die-
selbe Enigma wie im Heere benutzt wurde, sehr wesentlich von
denen des Heeres und der Luftwaffe. Es wäre daher unzweckmäßig
gewesen, wollte man die Ergebnisse, die auf diesem Gebiet er-
zielt wurden, chronologisch zwischen die übrigen Arbeiten ein-
flechten. Sie mögen jetzt am Ende dieser Skizze zusammenge-
stellt werden.
Die im Funkverkehr der deutschen Kriegsmarine vorkommenden
Sprüche werden stets verschlüsselt in zwei-, drei- oder vier-
stelligen Buchstabengruppen angegeben, wobei Teilgruppen (z.B.
am Ende des Spruches) nicht vorkommen. Hauptsächlich wurde die
vierstellige Chiffre benutzt und nur dieser wurde in der pol-
nischen Schlüsselstelle bearbeitet.
Die in den Jahren 1926 - 1927 angewandten vierstelligen Chiffres
waren stets überschlüsselte Satzbücher. Die erste und letzte
Gruppe eines jeden Spruches waren Blind- oder Kenngruppen.
Die übrigen Gruppen waren verschlüsselte Codegruppen. Weder die
Überschlüsselung noch die Satzbücher konnten gelöst werden.
In den Jahren 1926 - 1927 wurden zwei vierstellige Chiffres ange-
wandt. Einer von ihnen war ein gewöhnliches Satzbuch ohne
weitere Überschlüsselung. Dieses Satzbuch wurde im Jahre 1933
gelöst.
Die Codegruppen bestanden ausschließlich aus 18 Buchstaben:
A B E F G I K L N O P S T U W X Y Z
Das Satzbuch war sehr umfangreich und besaß wahrscheinlich über
90000 Codegruppen, von denen für ungefähr 10000 die Bedeutungen
gefunden worden konnten.
/* Der Zweite der beiden vierstelligen Chiffre war, wie sich
herausstellte, mittels einer Chiffriermaschine verschlüsselt.
35. Die Marine-Chiffriermaschine mit 29 Tasten
In der Zeit vom Januar 1926 bis September 1934 wurde von der
deutschen Kriegsmarine eine Chiffriermaschine zum Verschlüs-
seln von Funksprüchen benutzt. Die Maschine war eine Enigma-
Chiffriermaschine, die sich jedoch in folgenden Einzelheiten
von der im Heere gebrauchten Enigma-Chiffriermaschine unter-
schied:
1) Die Maschine besaß 29 Tasten und eben soviel Glühlampen für
die 29 Buchstaben des deutschen Alphabets mit den Umlauten.
2) Beim Niederdrücken der Taste X leuchtete stets die Glüh-
lampe X auf.
3) Weder Stöpselstellungen noch Steckerverbindungen waren
vorhanden.
4) Die Schaltung der Eintrittswalze war folgende:
A Ä B C D E F G H I J K L M
1 2 3 4 5 6 7 8 9 10 11 12 13 14
N O Ö P Q R S T U Ü V W X Y Z
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
5) Die Zahl der Chiffrierwalzen betrug fünf, von denen gleich-
zeitig drei in die Maschine eingesetzt wurden.
6) Die Zähne der Chiffrierwalzen waren nicht mit den Ringen,
sondern mit der Walzeneinfassung verbunden.
7) Die Umkehrwalze war beweglich; man konnte sie wie jede
Chiffrierwalze einstellen.
8) Die Ringe besaßen Zahlen von 1 - 28.
Obwohl diese Chiffriermaschine schon ab 1926 im Gebrauch war,
gelang es sie erst an Hand der Sprüche aus den Jahren 1931 - 1934
zu rekonstruieren. In dieser Zeit wurden die Sprüche auf die-
selbe Weise wie im Heere verschlüsselt, das heißt also, daß
für jeden Tag eine Grundstellung festgestellt wurde, bei wel-
cher der aus 3 Buchstaben bestehendes Spruchschlüssel zweimal
verschlüsselt wurde. Die so erhaltenen zwei dreistellige Buch-
stabengruppen wurden durch Voransetzung je eines blinden Buch-
stabe in vierstellige Gruppen verwandelt, von denen die erste
am Anfang und die zweite am Ende des Spruches eingesetzt wurde.
Auf diese beiden Gruppen konnte auf dieselbe Weise wie im Heer
die Zyklentheorie angewandt werden.
Das Bilden der Substitutionen A1A4, A2A5 und A3A6 war jedoch
dadurch erschwert, daß das Spruchmaterial unzureichend war.
Um so schwerer war es die Spruchschlüssel selbst zu erhalten.
Erst im Jahre 1933 wurde dies erheblich leichter, als sich
herausstellte, daß die Spruchschlüssel, die einem Verzeichnis
entnommen wurden, keine Umlautbuchstaben enthielten. Man kon-
nte jetzt die Zyklen so einander zu ordnen, daß Buchstaben die
in ersten Gruppe der verschlüsselten Spruchschlüssel nicht
vorkamen, auf Umlaute fielen.
Eine weitere Schwierigkeit beruhte in der Unkenntnis der
Schaltung der Eintrittswalze. Sie wurde jedoch glücklich er-
raten ebenso wie dies bei der Heeresmaschine geschehen war.
Man setzte dabei voraus, daß keine Steckerverbindungen vorhan-
den sind, was sich als richtig ergab. Im entgegengesetzten
Fall wäre die Rekonstruktion der Maschine wahrscheinlich ge-
scheitert. Und so fand man denn, ebenso wie im Heer, die
Walzenschaltungen.
Jetzt kehrte man zu den Sprüchen aus früheren Jahren zurück.
Im Jahre 1936 wurden innerhalb von Zeitabschnitten, die meh-
rere Tage umfaßten, sämtliche Sprüche von ein- und derselben
Position der Walzen ausgehend (also andere wie im Heere) ver-
schlüsselt. Um den Spruchinhalt in einem dieser Zeitabschnitte
zu finden, ging man folgendermaßen vor:
Man fand zwei Sprüche, die allem Anschein nach denselben
Spruchinhalt besaßen, wobei jedoch in einem Fall vom Schlüs-
sler ein Buchstabe ausgelassen worden war. Die entsprechenden
Buchstaben beider Sprüche mussten daher, nacheinander getastet,
denselben Klartext liefern. Mit Hilfe des Rostes erhielt man
die Position der rechten Walze und hierauf ohne besondere Schwie-
rigkeiten die Positionen der übrigen Walzen. Es stellte sich
heraus, daß Spruchinhalt nochmals mittels eines Satzbuches
verschlüsselt war, desselben, der gleichzeitig auch ohne Ma-
schinenverschlüsselung angewandt wurde, und der bereits teil-
weise gelöst war; es war der schon erwähnte, die 18 Buchstaben
ABEFGIKLNOPSTUWXYZ enthaltende vierstellige Code. Außer diesem
einen Zeitabschnitt wurden andere Zeitabschnitte nicht gelöst.
Man stellte nur fest, daß die Walzenlage, Stellung der Umkehr-
walze, Ringstellung und Spruchstellung (Grundstellung gab es
bei diesem Verfahren nicht) in unregelmäßigen Zeitabschnitten,
die 3 - 15 Tage umfaßten, verändert wurden.
Am 1. Januar 1927 wurde zwar nicht das Schlüsselverfahren,
wohl aber das Satzbuch durch ein neues ersetzt. Man konnte
jetzt die Schlüssel auf folgende Weise finden: In einer gan-
zen Reihe von Sprüchen vermutete man am Ende stets eine und
dieselbe Codegruppe, die "Fortsetzung folgt" bedeuten sollte.
Da die Maschine die Eigenschaft besitzt, daß Klar- und (mit
Ausnahme von X, das stets X ergibt), verschlüsselte Buchstaben
stets voneinander verschieden sind, konnte man schließlich
diese Gruppe (unverschlüsselt) finden, und hierauf mittels des
Rostverfahrens die Positionen der Walzen für einen Zeitabschnitt
bestimmen. Es stellte sich heraus, daß das neue Satzbuch sämt-
liche 29 Buchstaben einschließlich der Umlaute enthielt, es
konnte jedoch aus Zeitmangel nicht gelöst werden.
Am 1. Januar 1929 trat eine Änderung, diesmal des Schlüsselver-
fahrens selbst ein. Sie beruhte darauf, daß jetzt jeder Spruch
seine eigene Spruchstellung besaß, die mittels der am Anfang
und Ende jeden Spruches stehenden Kenngruppen auf eine uns
nicht näher bekannte Weise angegeben wurde.
Am 1. Mai 1931 trat eine erneute Änderung des Schlüsselver-
fahrens ein, die darauf beruhte, daß jetzt der Spruchschlüs-
sel ebenso geschlüsselt wurde wie im Heere. Gerade dadurch
gelang es ja die Walzenschaltungen zu rekonstruieren.
Es kam jetzt noch darauf an, den Spruchinhalt selbst zu finden.
Man vermutete zunächst als Inhalt Satzbuchgruppen, aber nach
mehreren Monaten angestrengter vergeblicher Arbeit stellte
es sich zufällig heraus, daß der Inhalt aus Klartext (ähnlich
wie im Heere) bestand. Das Schlüsselverfahren war, wie bereits
erwähnt wurde, grundsätzlich dasselbe wie im Heere und in der
Luftwaffe. Doch wurde die sogenannte "innere" Maschinenstel-
lung, d.h. Walzenlage, Stellung der Umkehrwalze, und Ringstel-
lung so wie bisher in unregelmäßigen Zeitabständen geändert,
während die Grundstellung täglich geändert wurde.
Die Spruchschlüssel wurden einem Verzeichnis entnommen. Sei
es, daß dies Verzeichnis nicht sehr umfassend war oder sei
es, daß die Schlüssler vorwiegend dieselben Spruchschlüssel
aus dem Verzeichnis wählten, jedenfalls wiederholten sich die-
selben oft, so daß eine Statistik angefertigt werden konnte
die es erlaubte aus den Substitutionen A1A4, A2A5, A3A6 die
(unverschlüsselten) Spruchschlüssel selbst zu finden, wobei
auch das Nichtvorkommen der Umlaute in den Spruchschlüssel
behilflich war.
Das Zyklometer konnte nicht angewandt werden, denn die Kata-
loge zu diesem müssten
60 · 284 = 36.879.360
Positionen umfassen, was wohl kaum ausführbar wäre. So wurde
denn die Position der rechten Walze mittels des Rostes fest-
gestellt, was mühelos geschah, da keine Steckerverbindungen
vorhanden waren, während die Position der übrigen Walzen mit
Hilfe einer Kartothek, ähnlich der Katalogen F im Heere und
in der Luftflotte, bestimmt wurde, nur war diese Kartothek
umfangreicher, denn sie enthielt
283 = 21952
Positionen.
Der Spruchinhalt selbst war so kurz wie möglich gefaßt. Es
kamen in ihm Wortkürzungen aller Art vor. Die zweiten und
weiteren Teile eines mehrteiligen Spruches begannen stets mit
den Buchstaben FORT (Abkürzung für Fortsetzung). Um Grundstel-
lung und Ringstellung gesondert zu finden, ging man von diesen
Buchstaben FORT aus, so wie man im Heer und in der Luftflotte
von den Buchstaben AN und im S.D. von den Buchstaben QY ausging.
36. Die Anwendung in der deutschen Kriegsmarine der Enigma-
Chiffriermaschine mit 26 Tasten.
Vom 1. Oktober 1934 ab wurde in der deutschen Kriegsmarine die-
selbe Enigma-Chiffriermaschine wie im Heere angewandt. Das
Chiffrierverfahren blieb dasselbe wie bisher, mit dem Unter-
schied, daß jetzt die Steckerverbindungen (stets 6 Paar) hin-
zutraten, die gleich der Grundstellung täglich geändert wurden.
In der Zeit bis zum 15. November 1936 wurden außerdem in der
deutschen Kriegsmarine zwei zusätzliche Chiffrierwalzen vor-
handen waren, von denen drei gleichzeitig in die Maschine ein-
gesetzt wurden.
Mit Hilfe der für das Heer hergestellten Kataloge zum Zyklo-
meter konnte nur ein kleiner Teil (etwa ein Zehntel) der Tage
bis zum 15. November 1936 gelöst werden. Dies genügte nicht
um ein Spruchschlüsselverzeichnis herstellen zu können. Erst
als am 16. November 1936 die beiden Zusatzwalzen zurückgezogen
wurden und nur die drei Walzen I, II, III übrig blieben,
konnte ein entsprechendes Spruchschlüsselverzeichnis herge-
stellt werden, mit Hilfe dessen man nachträglich die Spruch-
schlüssel in den Tagen vor dem 16. November auffinden konnte.
Hinterher mittels der Rostmethode wurden dann die Schaltungen
der beiden Zusatzwalzen errechnet. Man nannte sie IVM und VM
zum Unterschied von den später im Heer und in der Luftflotte
gebrauchten Walzen IV und V.
Für wichtigere Sprüche gab es außer dem allgemeinen noch einen
Offiziers- und einen Stabs- (oder Admirals-) Schlüssel. Der
Offiziersschlüssel wurde wie folgt angewandt: Zunächst wurde
der gewählte Spruchschlüssel bei der Grundstellung "Allgemein"
zweimal verschlüsselt und die beiden so erhaltenen dreistel-
lige Buchstabengruppen nach Voransetzung eines vierten Füll-
buchstaben wie üblich als erste und letzte Gruppe in den Spruch
eingesetzt. Hierauf jedoch wurde der gewählte Spruchschlüssel
noch einmal bei der Grundstellung "Offizier" verschlüsselt und
das Ergebnis (und nicht der Spruchschlüssel selbst) diente zur
Schlüsselung des eigentlichen Spruchinhaltes.
Wie der Stabsschlüssel angewandt wurde ist nicht bekannt. Am
1. Mai 1937 trat eine Änderung des Schlüsselverfahrens ein,
die darauf beruhte, daß der Spruchschlüssel nicht mehr mit-
tels der Maschine selbst, sondern auf eine andere, ziemlich
komplizierte Weise verschlüsselt wurde. Die Einzelheiten des
neuen Schlüsselverfahrens wurden erst bekannt, als es in Jahre
1940 den Engländern gelang, in einem versunkenen deutschen
U-Boot die Schlüsseleinleitung zu diesem Verfahren zu finden.
Wir können dies Verfahren hier nicht ausführlicher beschrei-
ben, sondern verweisen den Leser auf die photographische Ab-
bildung der Schlüsselanleitung.
Die Unkenntnis des neuen Schlüsselverfahrens hinderte uns
nicht im Jahre 1937 eine Reihe von Ergebnissen zu erzielen,
die hier mitgeteilt werden mögen.
Der Spruchschlüssel wird in jedem Spruch mittels der beiden
ersten Gruppen angegeben, die zwecks Vermeidung von Fehlern
am Ende des Spruches wiederholt werden. Der eigentliche Text
also beginnt mit der dritten Gruppe. Mittels einer Methode
die nach angegeben wird, gelang es den Textinhalt vieler
Sprüche zwischen den 1. Mai und 8. Mai 1937 zu finden und
dadurch die Walzenlage, Steckerverbindungen, sowie teilweise
auch die Ringstellung zu rekonstruieren. Ein Vergleich mit
den gelösten Tagen von Ende April 1937 ergab, daß die innere
Einstellung am 1. Mai 1937 keiner Änderung unterlag, und daß
sie in der Zeit vom 27. April bis 8. Mai dieselbe geblieben ist.
Ein Vergleich der Spruchschlüssel der gelösten Sprüche mit
beiden ersten (oder letzten) Gruppen ergab folgendes:
Werden in sämtlichen gelösten Sprüchen eines Tages die beiden
ersten Gruppen in vier nebeneinander stehende Buchstabenpaare
geteilt und haben zwei Sprüche ein gemeinsames erstes, zweites
oder drittes Buchstabenpaar, so haben sie auch einen gemein-
samen ersten, zweiten oder dritten Spruchschlüsselbuchstaben.
Die umgekehrte Behauptung ist nicht wahr. Gleichen Buchstaben
können also sehr wohl verschiedene Buchstabenpaare entsprechen.
Auch entsprechen gleichen Buchstabenpaaren an verschiedenen
Stellen im Allgemeinen verschiedenen Spruchschlüsselbuchstaben.
Bei der Änderung des Verfahrens am 1. Mai 1937 wurde außer der
Beibehaltung der inneren Einstellung noch ein zweiter grober
Fehler durch die Schlüsselstelle der deutschen Kriegsmarine
begangen. Da ein Kriegsschiff nicht rechtzeitig mit der neuen
Schlüsselmethode versehen werden konnte, verkehrte es noch
während der drei ersten Maitage 1937 nach dem alten Verfahren.
Auf diese Weise konnte man am 2. und 3. Mai 1937 die Grund-
stellungen "Allgemein" und "Offizier" auffinden.
Von Seiten der Engländer wurde später folgendes festgestellt:
Werden die Spruchschlüssel der nach neuen Verfahren geschlüs-
selten Sprüche mittels der gefundenen Grundstellungen vom 2.
und 3. Mai entschlüsselt, so entsprechen denselben Buchstaben-
paaren dieselben Buchstaben der entschlüsselten Spruchschlüssel,
selbst wenn sie an verschiedenen Stellen auftreten.
Der Inhalt der Sprüche in der Periode vom 1. Bis 8. Mai 1937
wurde auf folgende Weise gefunden: Nahmen wir an wir hätten
einen Spruch, der nach der Streichung der zwei ersten Gruppen
folgendermaßen beginnt:
VLPP WGKS WKUL QBOR
Weiterhin nehmen wir an, daß dieser Spruch die Fortsetzung
eines anderen Spruches sei, der im Kopfe die Uhrzeit 1623 trägt.
Nach unseren Erfahrungen muß dann Klartext dieses Spruches mit
den Buchstaben
F O R T Y Q Z W E Y Y Q Z W E Y
beginnen (QZWE bedeutet 1623). Wir kennen also ein aus 16 Buch-
staben bestehendes Fragment des Textes vor und nach der Ver-
schlüsselung. Da in der Marine stets nur 6 Paar Steckerverbin-
dungen auftreten, muß ein Teil der Buchstaben unverändert bleiben.
Man macht nun verschieden Annahmen darüber, welche Buchstaben
unverändert geblieben sind, und sucht diese Annahmen zu veri-
fizieren, entweder direkt auf der Maschine, oder mittels des
Rostes, oder mit Hilfe der Bogen Jeffreys, einer englischen
Erfindung, die unseren Katalogen F entsprach. In allen Fällen
ist die Arbeit sehr lang, so daß sie sich nur dann lohnt, wenn
es wie in unserem Falle, darauf ankommt, ein neues Verfahren
zu analysieren.
Den Engländern gelang es noch einige Sprüche vom Jahre 1938
zu lösen. Hieraus ging hervor, daß jetzt die Umkehrwalze B im
Gebrauch ist. Wahrscheinlich wurde sie in derselben Zeit wie
im Heer eingeführt. Die Zahl der Steckerverbindungen blieb
weiterhin 6 Paar.
Im Jahre 1940 fanden die Engländer in einem gesunkenen deu-
tschen U-Boot zwei Chiffrierwalzen, die die Bezeichnung VI
und VII trugen. Ob jetzt in der Marine die fünf Walzen I, II,
III, VI und VII, oder sämtliche Walzen I bis VII angewandt
werden, muß dahingestellt bleiben.
| 37. Chronologische Übersicht über die Anwendung von Enigma-Chiffriermaschinen in der deutschen Kriegsmarine |
|---|
| 1926 | 1927 | 1928 | 1929 | 1930 | April 1931 | Mai 1931 | 1932 | 1933 | September 1934 | Oktober 1934 | 1935 | 15. November 1936 | 16. November 1936 | April 1937 | Mai 1937 | Oktober 1937 | November 1937 | 1938 | 1939 | 1940 |
| Marine-Chiffriermaschine "Enigma" (29 Tasten) | Chiffriermaschine "Enigma" (26 Tasten) |
| 5 Chiffrierwalzen | Umkehrwalze A | Umkehrwalze B |
| Innere Einstellung: Walzenlage, Einstellung der Umkehrwalze und Ringstellung | 5 Ch.-Walzen I, II, III, IVM und VM | 3 Ch.-Walzen I, II, III | 5 Ch.-Walzen I, II, III, VI und VII |
| Innere Einstellung: Walzenlage, Einstellung der Umkehrwalze und Ringstellung Innere Einstellung ändert in unregelmäßigen Zeitabschnitten (3 - 15 Tage) |
| Die Grundstellung ändert gleichzeitig mit der inneren Einstellung | Grundstellung täglich geändert | Grundstellung und Steckerverbindung ändern täglich |
| Spruchschlüssel = Grundstellung | Das erste Schlüsselverfahren | Das zweite Schlüsselverfahren | Das dritte Schlüsselverfahren |
| 18 Buchstaben Code | 29 Buchstaben Code | Klartext |
38. Teilnahme der drei Staaten an der Lösung der Enigma
I. Polen
Zyklentheorie
Substitutionentheorie
Schaltungen der Walzen I - III und der Umkehrwalze A
Methode zur Auffindung der Eintrittswalze
Methode zur Auffindung der Steckerverbindungen
Methode der charakteristischen Schlüssel
Statistische Methode
Methode ungleicher Buchstaben
Bestimmung der rechten Walze
Der Rost und Katalog F
Zyklometer (Maschine und Katalog)
Auffindung des Textes
Schaltungen der Umkehrwalze B
Schaltungen der Walzen IV und V
Analyse des zweiten Schlüsselverfahrens
Die Bomben
Die Netze (Projekt)
Kataloge zu den Netzen (Projekt)
Analyse des dritten Schlüsselverfahrens
Das Funknetz S.D.
Die Marine-Enigma mit 29 Tasten
Schaltungen der Walzen IVM und VM
Analyse der Marine-Schlüsselverfahren vom 1. Mai 1937
II. England
Die Netze (Ausführung)
Kataloge zu den Netzen (Ausführung)
Methode Jeffreys
Methode Knox
Methode Herivel
Walzen VI und VII (im U-Boot gefunden)
III. Frankreich
Lieferung zweier wichtigen Dokumente
 ist folgende:
A:ai→bi (i = 1, 2, i… , n).
Mitunter ist es zweckmäßig, eine Permutation als einein-
deutige Abbildung der Menge der Restklassen (im zahlen-
theoretischen Sinne) modulo n auf sich anzusehen. Es wird
wie folgt verfahren:
Wir lassen als Indexe der Elemente ai sowie als Elemente
selber alle ganzen Zahlen zu und identifizieren
ai + tn (-∞ < t < +∞, 1 ≤ i ≤ n) bzw.
ai + tn (-∞ < t < +∞, 1 ≤ ai ≤ n) mit ai.
Wenn in einer Relation zwischen Permutationen oder deren
Elemente als Elemente außer 1, 2, …, n auch andere
ganze Zahlen auftreten oder auftreten können, so gebrauchen
wir das Zeichen
ist folgende:
A:ai→bi (i = 1, 2, i… , n).
Mitunter ist es zweckmäßig, eine Permutation als einein-
deutige Abbildung der Menge der Restklassen (im zahlen-
theoretischen Sinne) modulo n auf sich anzusehen. Es wird
wie folgt verfahren:
Wir lassen als Indexe der Elemente ai sowie als Elemente
selber alle ganzen Zahlen zu und identifizieren
ai + tn (-∞ < t < +∞, 1 ≤ i ≤ n) bzw.
ai + tn (-∞ < t < +∞, 1 ≤ ai ≤ n) mit ai.
Wenn in einer Relation zwischen Permutationen oder deren
Elemente als Elemente außer 1, 2, …, n auch andere
ganze Zahlen auftreten oder auftreten können, so gebrauchen
wir das Zeichen  , wenn es sich um Permutationen han-
delt, und die Kongruenzschreibweise der Zahlentheorie oder
das Zeichen
, wenn es sich um Permutationen han-
delt, und die Kongruenzschreibweise der Zahlentheorie oder
das Zeichen  , wenn es sich um Elemente handelt. Wenn
von 1, 2, …, n verschiedene Indexe auftreten, so
behalten wir die gewöhnliche Schreibweise bei.
Im folgenden wird ist T stets die Permutation
, wenn es sich um Elemente handelt. Wenn
von 1, 2, …, n verschiedene Indexe auftreten, so
behalten wir die gewöhnliche Schreibweise bei.
Im folgenden wird ist T stets die Permutation




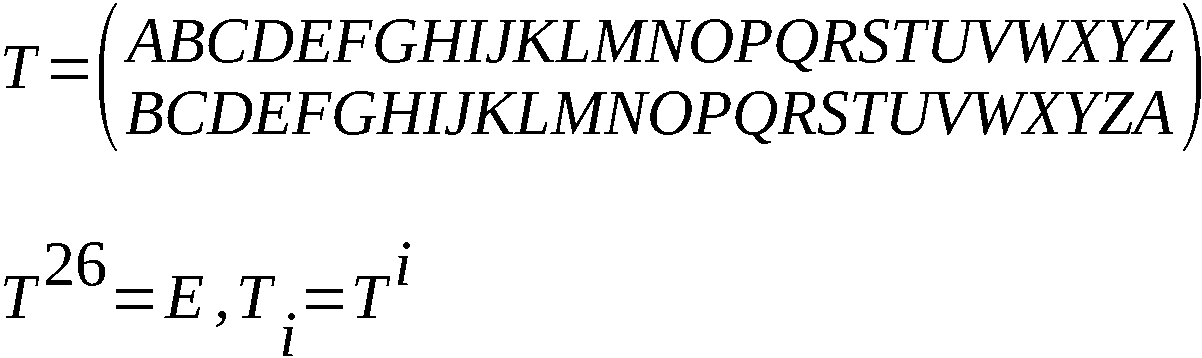
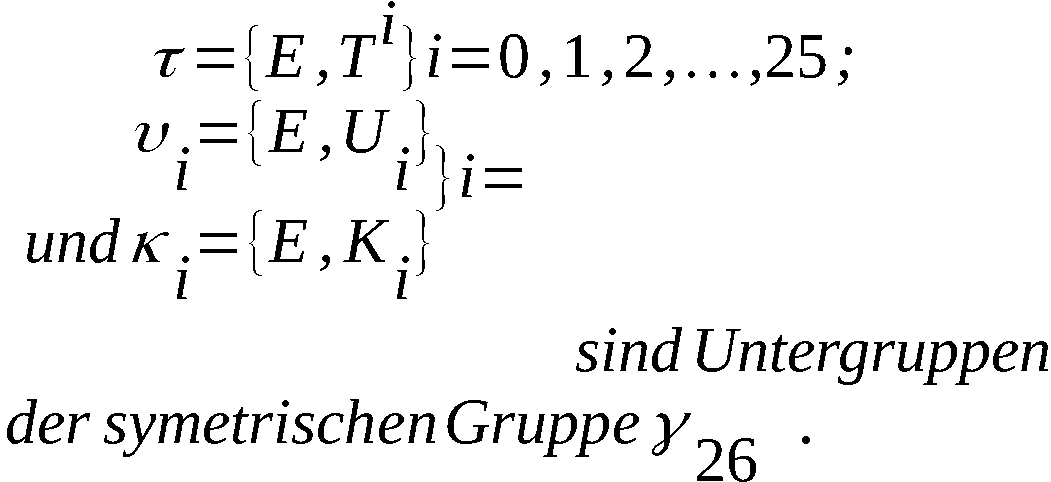

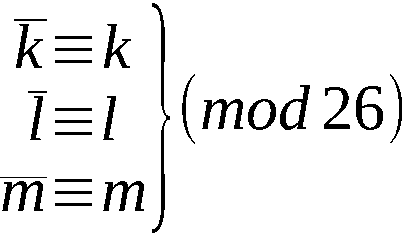


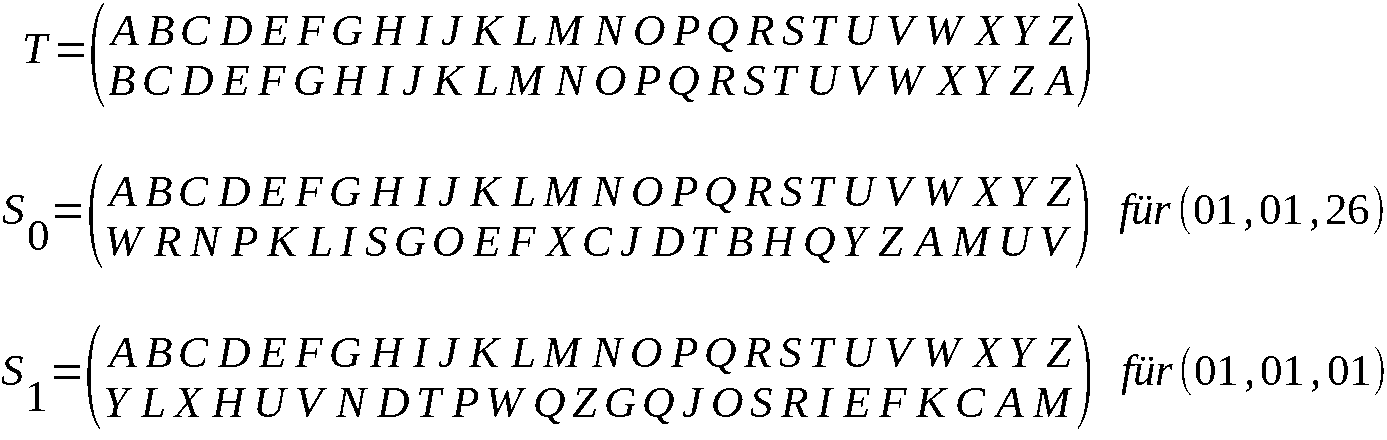



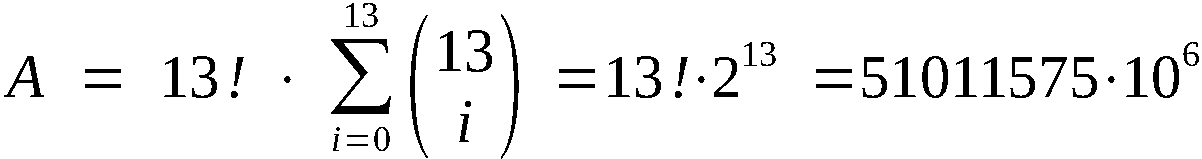

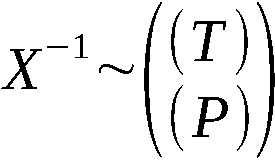




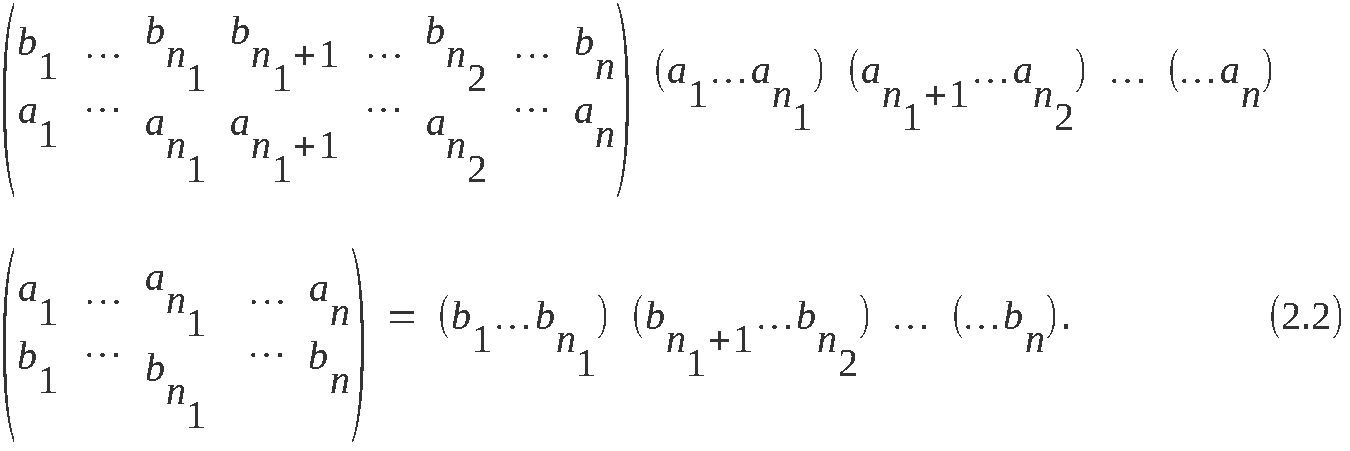

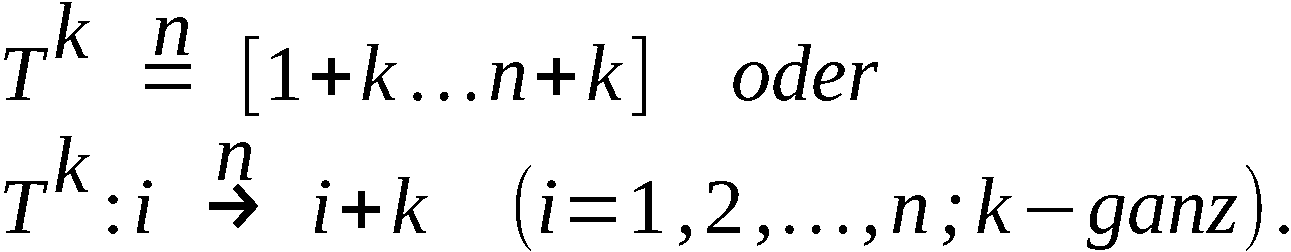
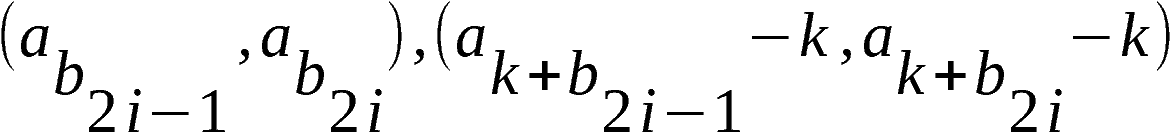
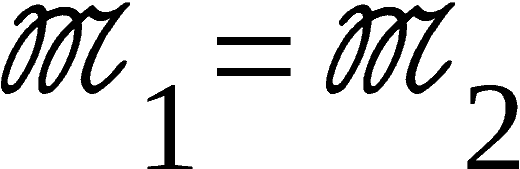
 (5.2)
(5.2)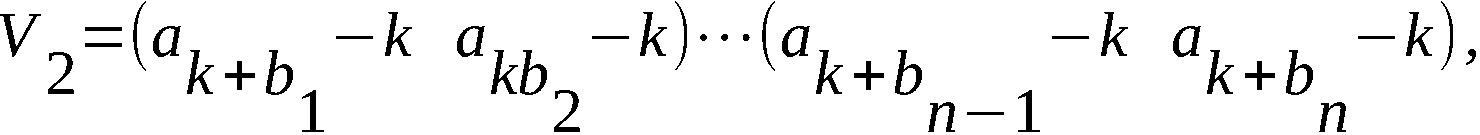 (5.3)
(5.3) .
Wir zeigen zunächst die Äquivalenz beider Sätze.
S a t z II
.
Wir zeigen zunächst die Äquivalenz beider Sätze.
S a t z II  (6.1)
(6.1)
 . Unter Ausnutzung
der Formel (2.2) erhalten wir folgnde Beziehung:
. Unter Ausnutzung
der Formel (2.2) erhalten wir folgnde Beziehung:

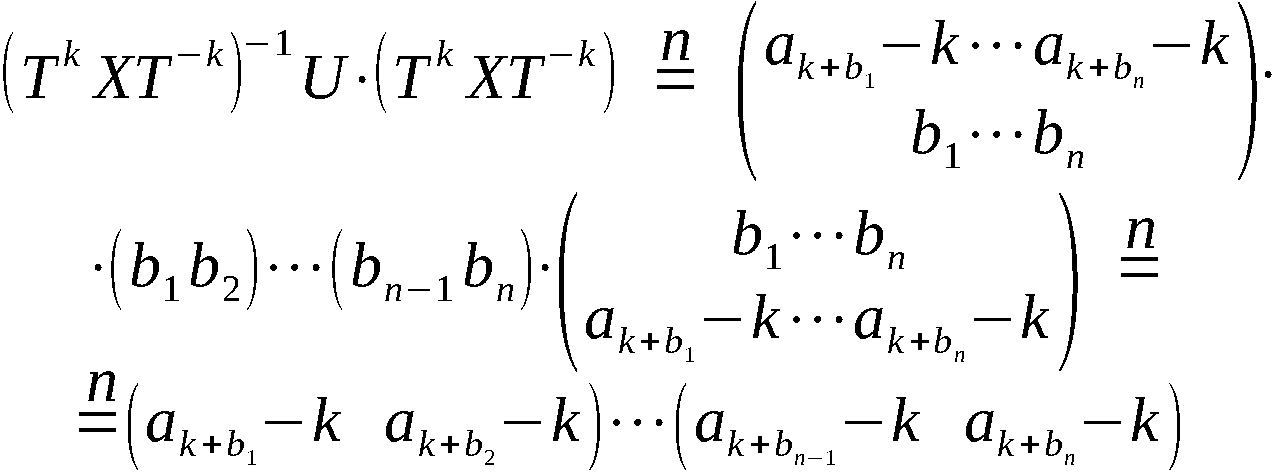
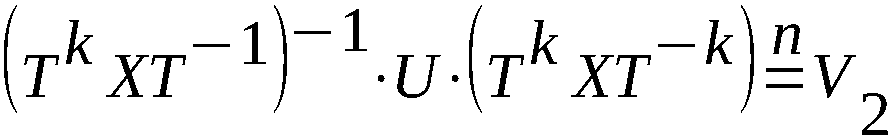 (7.2)
(7.2)
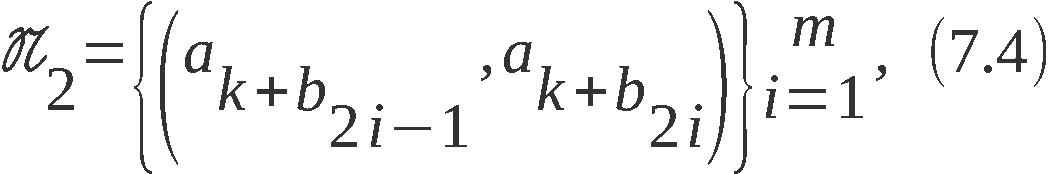
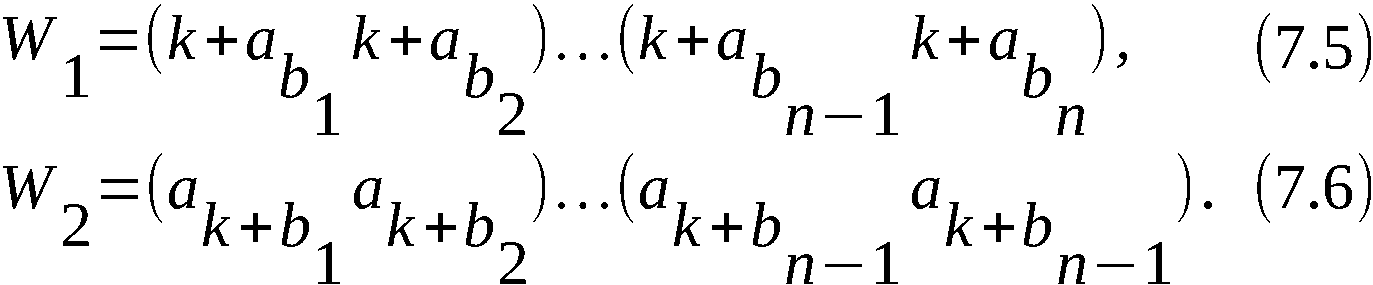

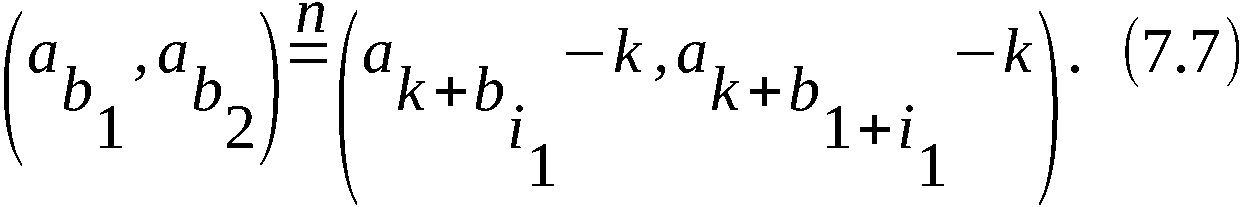

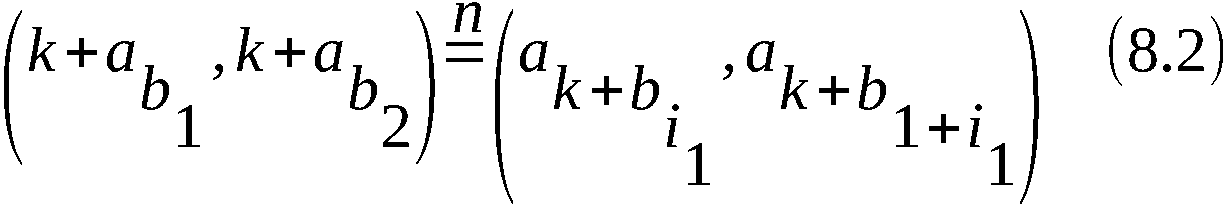
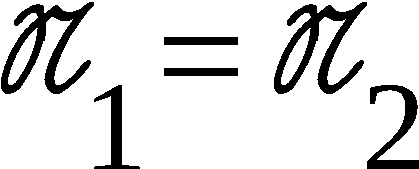 ,
4.
,
4.  .
3.2 Ein Algorithmus zur Bestimmung lösender k
Wir geben nun einen Algorithmus an, der es gestattet, bei
festen U und X eventuell vorhandene lösende K der Gleichung
(5.1) zu finden. Wir stützen uns dabei auf die Sätze I und II
und gehen vom Gleichungssystem (6.1) aus. Für n führt
der Algorithmus vermutlich schneller zum Ziel als direktes
Einsetzen aller k in (5.1) und Ausrechnen. Ein erläuterndes
Beispiel folgt im Anschluß an die Darlegung.
Die Frage, ob sich aus dem vorliegenden Algorithmus weitere
Gesetzmäßigkeiten über die Lösung der Gleichung (5.1)
gewinnen lassen, wurde aus Zeitmangel offengelassen. Sie
verdient meines Erachtens Aufmerksamkeit.
Kommen wir nun zum Algorithmus selber, der in m Schritte
zerfällt:
1.) Die erste Gleichung des Systems (6.1) lautet
.
3.2 Ein Algorithmus zur Bestimmung lösender k
Wir geben nun einen Algorithmus an, der es gestattet, bei
festen U und X eventuell vorhandene lösende K der Gleichung
(5.1) zu finden. Wir stützen uns dabei auf die Sätze I und II
und gehen vom Gleichungssystem (6.1) aus. Für n führt
der Algorithmus vermutlich schneller zum Ziel als direktes
Einsetzen aller k in (5.1) und Ausrechnen. Ein erläuterndes
Beispiel folgt im Anschluß an die Darlegung.
Die Frage, ob sich aus dem vorliegenden Algorithmus weitere
Gesetzmäßigkeiten über die Lösung der Gleichung (5.1)
gewinnen lassen, wurde aus Zeitmangel offengelassen. Sie
verdient meines Erachtens Aufmerksamkeit.
Kommen wir nun zum Algorithmus selber, der in m Schritte
zerfällt:
1.) Die erste Gleichung des Systems (6.1) lautet
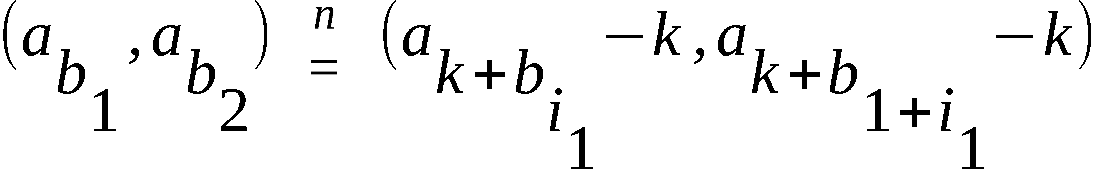 (9.1)
(9.1)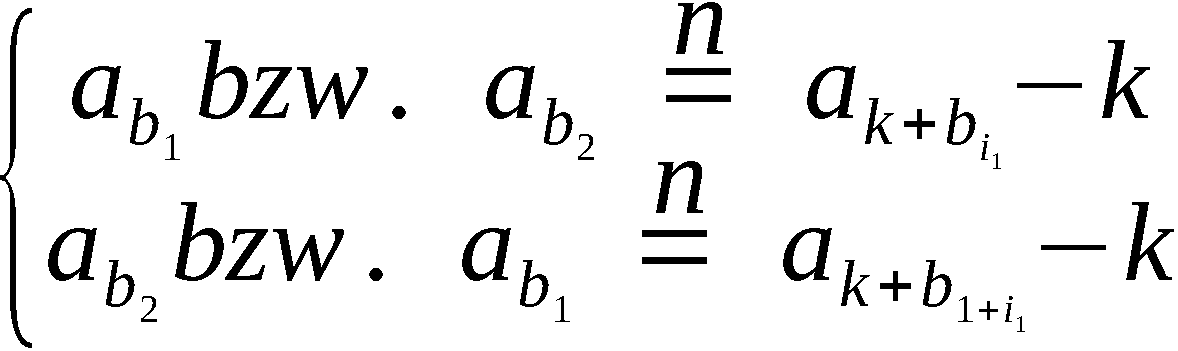
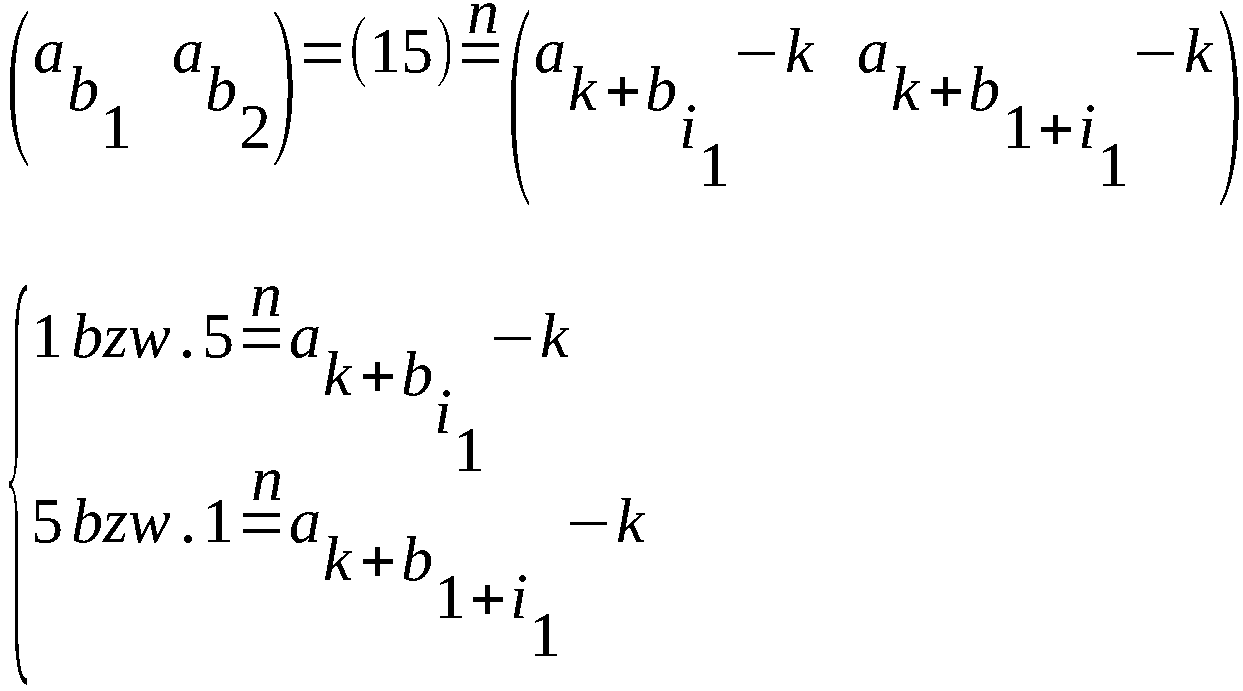
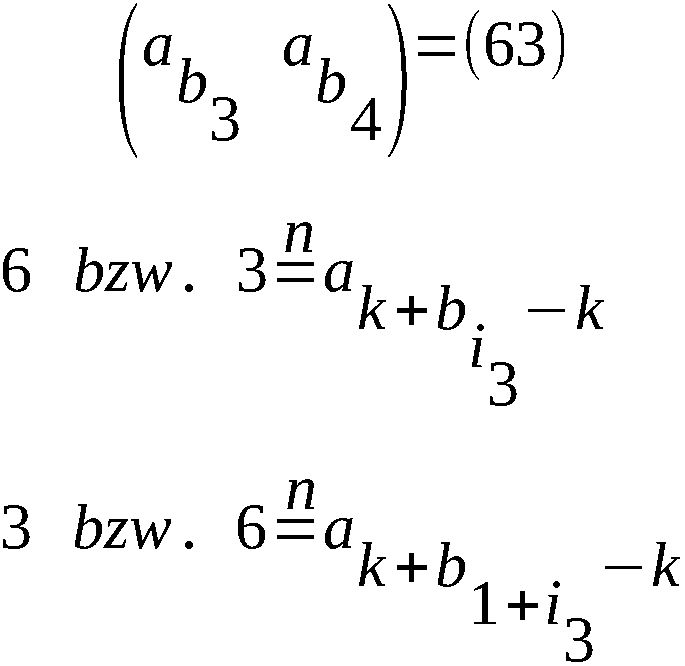




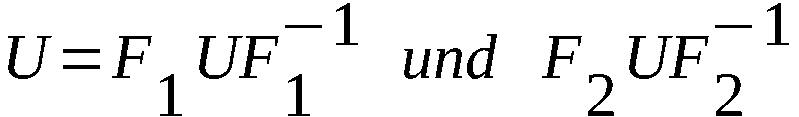



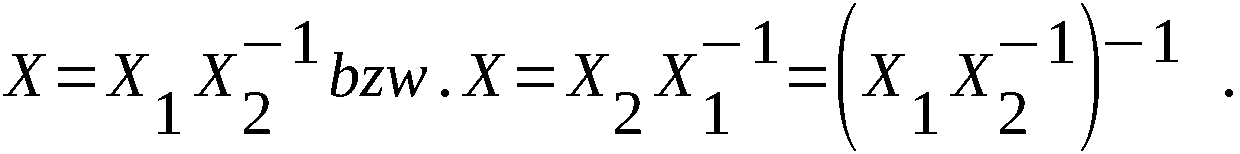

 bekannt.
Man benutzt nun die rechte Seite der ersten Gleichung des
Systems (6.1) und setzt o.B.d.A. i
bekannt.
Man benutzt nun die rechte Seite der ersten Gleichung des
Systems (6.1) und setzt o.B.d.A. i
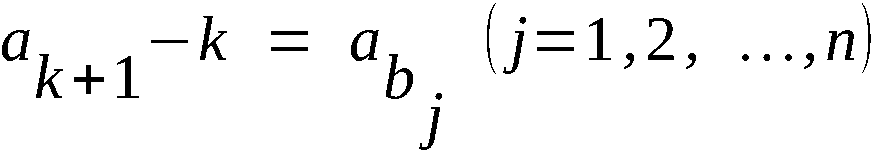 .
Wenn für das gleiche k
.
Wenn für das gleiche k
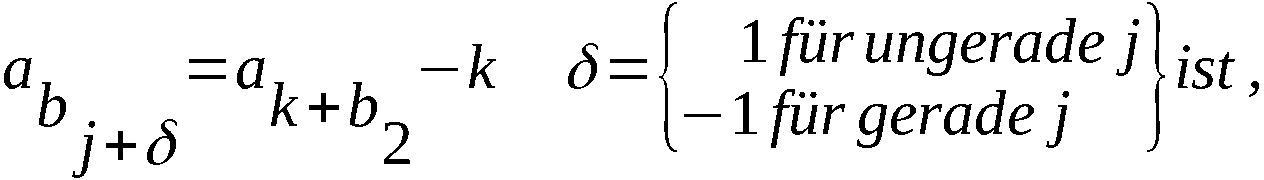
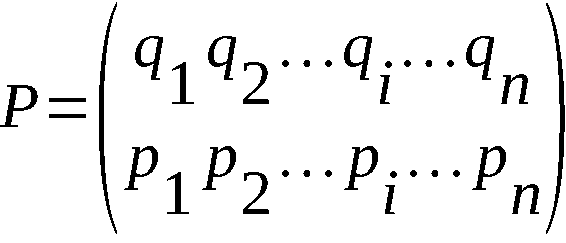


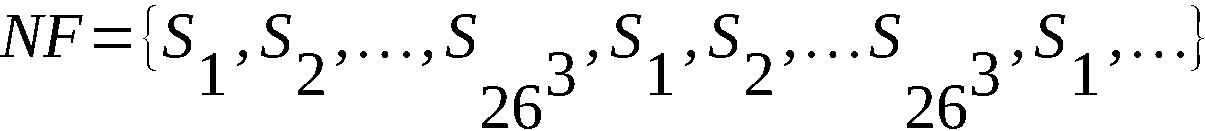
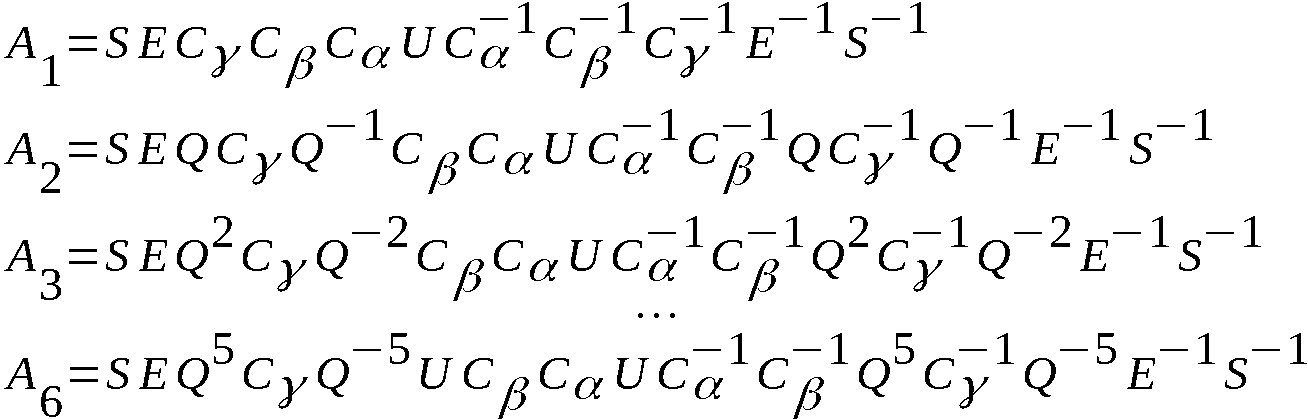



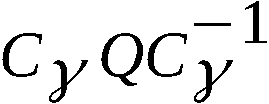 und hierdurch unmittelbar C
und hierdurch unmittelbar C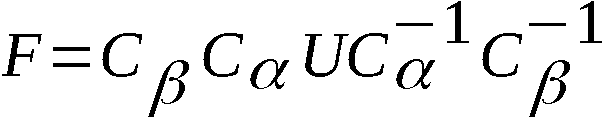

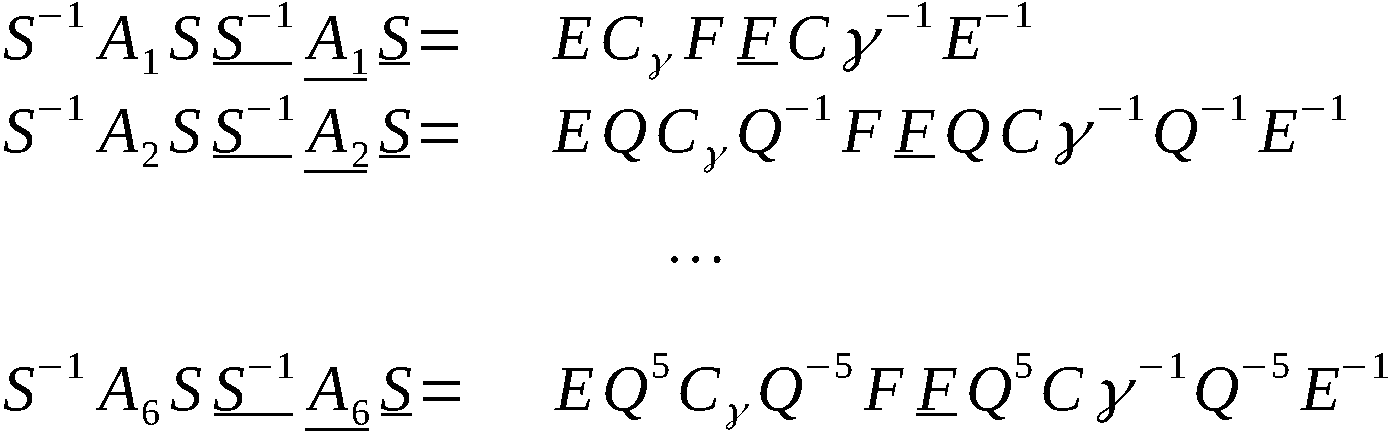

 zunächst
zunächst  ,
und hieraus unmittelbar E.
Der Weg zum Ergebnis ist recht lang, besonders wenn die Substi-
tutionen A
,
und hieraus unmittelbar E.
Der Weg zum Ergebnis ist recht lang, besonders wenn die Substi-
tutionen A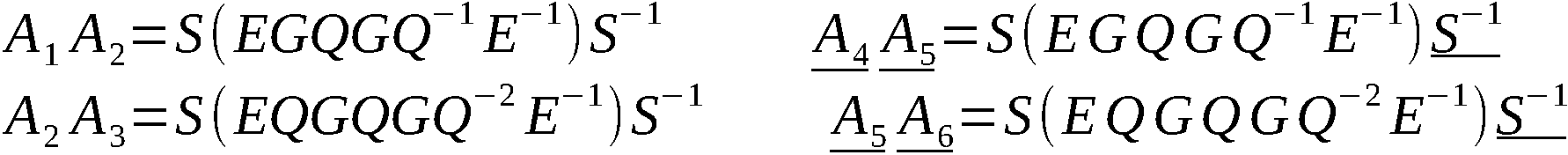
 gesetzt hat.
Ferner kann man aus den Gleichungen A
gesetzt hat.
Ferner kann man aus den Gleichungen A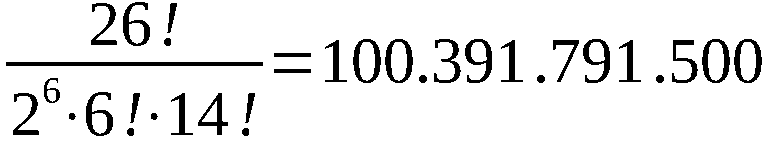
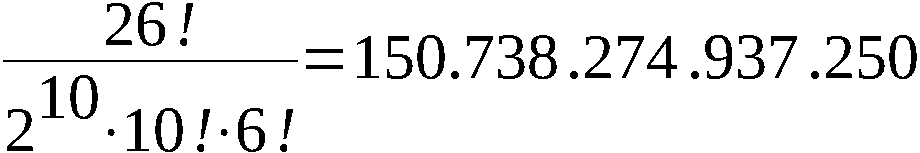


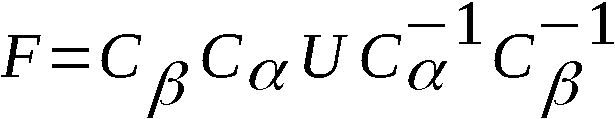 und des Exponenten X. Denn wenn wir
auch dank der vorliegenden Methode wissen, welche Walze sich
auf der rechten Seite befindet, so wissen wir doch nicht,
welches ihre Position ist.
Wir verfahren also auf die Weise, daß wir für X der Reihe
nach die Werte von 0 bis 25 einsetzen und jedesmal F aus jeder
der sechs Gleichungen errechnen. Die sechs Substitutionen F
werden jedesmal untereinander verschieden seines mit Ausnahme
einzigen Falles, wo sie sämtlich denselben Wert annehmen.
Auf diese Weise erhalten wir X, d.h. die Position der rechten
Walze und zugleich auch die Substitution F, die wir noch spä-
ter benötigen werden.
In der Praxis geht man in der Weise vor, daß man auf einem
Bogen Papier der Reihe nach die zweiten Zeilen der Substitu-
tionen
und des Exponenten X. Denn wenn wir
auch dank der vorliegenden Methode wissen, welche Walze sich
auf der rechten Seite befindet, so wissen wir doch nicht,
welches ihre Position ist.
Wir verfahren also auf die Weise, daß wir für X der Reihe
nach die Werte von 0 bis 25 einsetzen und jedesmal F aus jeder
der sechs Gleichungen errechnen. Die sechs Substitutionen F
werden jedesmal untereinander verschieden seines mit Ausnahme
einzigen Falles, wo sie sämtlich denselben Wert annehmen.
Auf diese Weise erhalten wir X, d.h. die Position der rechten
Walze und zugleich auch die Substitution F, die wir noch spä-
ter benötigen werden.
In der Praxis geht man in der Weise vor, daß man auf einem
Bogen Papier der Reihe nach die zweiten Zeilen der Substitu-
tionen  folgendermaßen aufschreibt:
(die ersten Zeilen der Substitutionen würden stets lauten
1 2 3 4 … 26)
7 19 3 15 23 11 20 4 16 26 10 14 22 2 17 6 25 9 1 21 12 18 5 24 13 8
16 2 14 22 10 19 3 15 25 9 13 21 1 16 5 24 8 26 20 11 17 4 23 12 7 6
1 13 21 9 18 2 14 24 8 12 20 26 15 4 23 7 25 19 10 16 3 22 11 6 5 17
: :
(das Beispiel ist willkürlich)
Hierauf schreib man auf einem zweiten Bogen mit Öffnungen
(daher der Name Rost) die 6 Substitutionen A
folgendermaßen aufschreibt:
(die ersten Zeilen der Substitutionen würden stets lauten
1 2 3 4 … 26)
7 19 3 15 23 11 20 4 16 26 10 14 22 2 17 6 25 9 1 21 12 18 5 24 13 8
16 2 14 22 10 19 3 15 25 9 13 21 1 16 5 24 8 26 20 11 17 4 23 12 7 6
1 13 21 9 18 2 14 24 8 12 20 26 15 4 23 7 25 19 10 16 3 22 11 6 5 17
: :
(das Beispiel ist willkürlich)
Hierauf schreib man auf einem zweiten Bogen mit Öffnungen
(daher der Name Rost) die 6 Substitutionen A