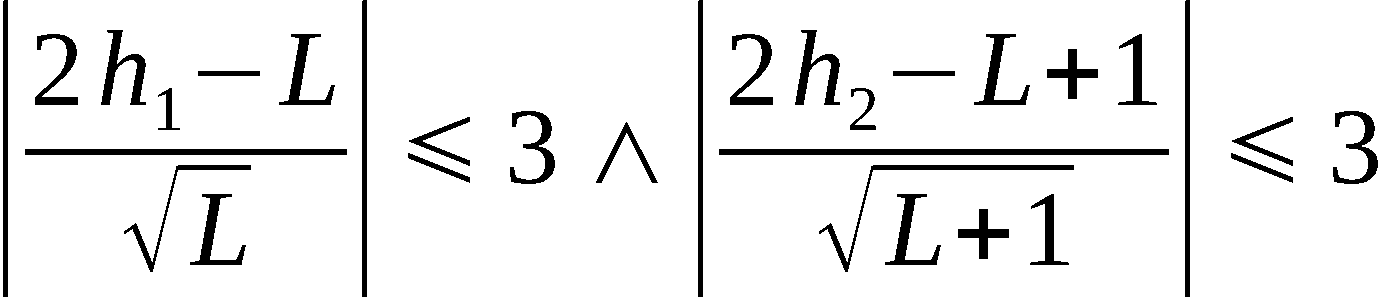Geräte und Maschinen der Schlüsselmittelproduktion
BArch*60, *105, *126, *157, *680, *682 … *687 *716
- Software der Schlüsselmittelproduktion
- Studie MISCHUNG - Permutation; 1980
- I-400 individuelle und zirkulare Schlüssellochstreifen - Produktion
- I-409 zirkulare Schlüssellochstreifen - Produktion
- SOEMTRON 527 und 528
- T-010 - T-046 weitere Geräte und Maschinen der Schlüsselmittelproduktion
- T-101 Rauschgenerator
- T-102 .
- T-103 .
- T-104 .
- T-105 .
- T-106 .
- T-107 .
- T-108 .
- T-109 .
- T-110 .
- T-111 .
- T-113 .
- T-150 Rauschgenerator mit Stanzeinrichtung, Folgenkontroll- und zähleinrichtung, Streifenvergleich
- T-151 Rauschgenerator mit Stanzeinrichtung, Folgenkontroll- und zähleinrichtung, Streifenvergleich
- T-153 Rauschgenerator mit Stanzeinrichtung, Folgenkontroll- und zähleinrichtung, Streifenvergleich
- T-200 Schreib- und Zählmaschine
- T-202 Kombinator und Vergleicher
- T-203 Schreibautomat
- T-203 Schreibautomat mit Kugelkopf
- T-251 Nebeneinanderschreiben
- T-253 Streifenschreibmaschine mit Kugelkopf
- T-601 Netzteil
- T-602 Vergleicher
- T-603 Modul-Prüfgerät
- T-814 Aufspuleinrichtung
- T-815 Papierschneide- und Aufspuleinrichtung
- T-817 Querschneideeinrichtung
- M-10 10fach Lochstreifenvervielfältiger
Rauschgenerator T-101
Freigabe für die Produktion ab 1967.
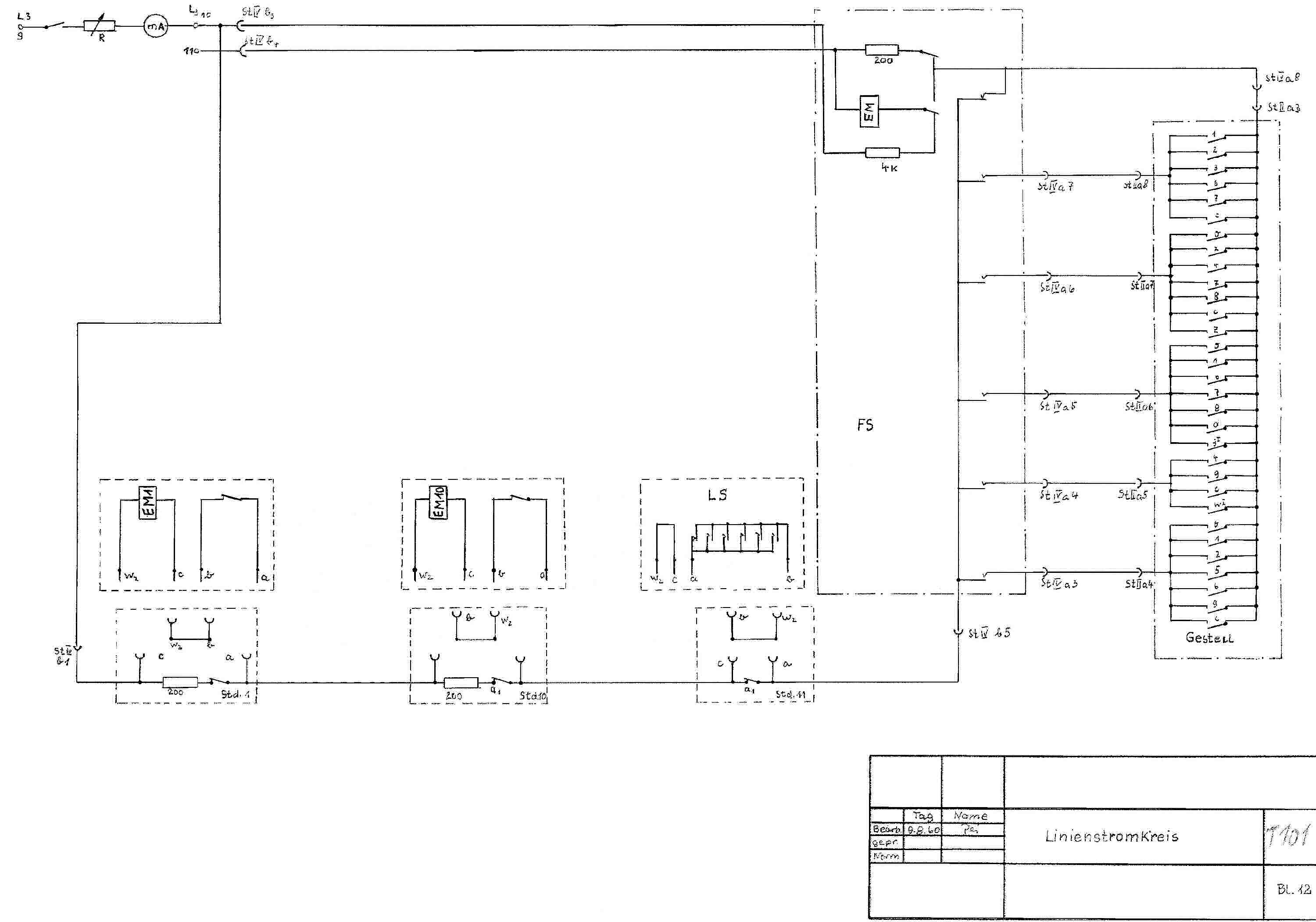
Abb.: T-101 Stromlaufplan
Rauschgenerator T-102
Freigabe für die Produktion ab 1967.
Rauschgenerator T-103
Bedingte Freigabe für die Produktion ab 1967, aber hohe Ausschußquote.
Rauschgenerator T-104.
Das Gerät T-104 dient zur Herstellung von Handschlüssel-
unterlagen und Schlüssellochstreifen.
80 Würfelgeneratoren, Rauschgeneratoren, arbeiteten ca. 16 Stunden
am Tag um den Bedarf an Schlüsselunterlagen zu decken.
Es kam zu verspäteten Freigabe für die Produktion wegen schlechter Zufallsfolgen.
Ein Gerät bestand aus einem Schreibwerk, einer Tastatur und drei
Lochstreifenlesern. Desweiteren mußte ein Zeichenzählgerät, ein
Doppellochstreifenleser oder Programmlocher und eine Aufwickeleinrichtung,
ähnlich dem DARO-System, angeschlossen werden.
Die Tastatur bestand im wesentliche aus folgenden Schaltern:
Netz (Gerätesystem Ein- Ausschalten)
Schreibwerk (Einschalten des Schreibwerkes mit der Vorgabe 0-9 oder 26, SOEMTRON 527
Locher
Halt (Anhalten des Laufes bei Störungen)
Locher EIN (Einschalten der Locher)
Betrieb
W (Einschalten des Zählwerks)
S1 (Zeichenzähler des Lochstreifenleser 1)
S2 (Zeichenzähler des Lochstreifenleser 2)
Programm (Programmleser, zählt WR, ZV, ZL)
0-9 (Zahlenausgabe, keine Mischtexte)
26 (Ausgabe von Buchstabentexten, keine Mischtexte)
32 (Schalter quittiert das Auftreten einer 32.ten Kombination)
Schritt (Quittieren der Prüfung des aktuellen Schrittes, Spaltenzähler des Schreibwerkes)
Die Ausgabe der Zahlen erfolgt durch die Kombination folgender Buchstaben:
K-Q-F = 1 R-L-Zv = 4 U-J-Zi = 7
A-W-X = 2 N-T-Wr = 5 I-G-M = 8
E-D-Z = 3 Y-S-B = 6 H-O-Zw = 9 V-C-P = 0
In der Modifikation der T-104/5 erfolgte die Zahlenausgabe nach folgender Lochkombination:
Kanal 1 A-W-X = 2 E-D-Z = 3
Kanal 2 U-K-Zi = 7 P-L-Zv = 0
Kanal 3 I-C-F = 8 S-Y-Zw = 6
Kanal 4 B-O-J = 2 R-Wr-N = 4
Kanal 5 H-T-M = 5 Q-V-G = 1
Die Auswertung der Zufallsfolgen erfolgte mit dem Programm P-640 und P-636.

Abb.: Übersichtsschaltbild T-104/5.
Rauschgenerator T-105
Der Rauschgenerator T-105 wurde 1966 vom ZCO entwickelt und erbaut.
Er basiert auf die Patentschrift Nr. 958-933 und dem Zufallsgenerator
der Firma Reichert.
In der Patentschrift werden fünf unabhängige Rauschgeneratoren
zur Bildung von 5 Kanal Lochstreifen oder zur Ansteuerung,
über eine Diodenmatrix, einer 36 Typen Schreibmaschine die Zufallsfolgen ausdruckt.
Basis des Rauschgenerators ist eine Vierschichtdiode. Diese erzeugt Sägezahnsignale.
Diese werden zu einem Flip-Flop geführt.
Wenn die Schwingung der Vierschichtdiode abbrechen, abgeschaltet wird, verbleibt das Flip-Flop
in seine letzte Lage. Es wird dann eine 0(0 V) oder 1(-14 V) ausgegeben.
Für die Transistoren der Flip-Flopschaltung wurde festgelegt das die Stromverstärkung
nicht größer als 100 sein soll und diese paarig auszumessen sind (50 - 70).
Mit dem Kondensator C2, siehe Abb.1 der parallel zur Vierschichtdiode liegt, kann die
Frequenz variiert werden. Diese sollte folgende Bedingung erfüllen:
f1 * f2 >= 1600 Hz.
Die Dimensionierung der fünf Kanäle ist wie folgt festgelegt worden:
Kanal 1 f1 = 150 kHz f2 = 20ms +- 2ms
Kanal 2 f1 = 120 kHz f2 = 20ms +- 2ms
Kanal 3 f1 = 120 kHz f2 = 20ms +- 2ms
Kanal 4 f1 = 110 kHz f2 = 20ms +- 2ms
Kanal 5 f1 = 125 kHz f2 = 20ms +- 2ms
f1 = Schwingfrequenz; f2 = Anstoßzeit

Abb. 1: Rauschgenerator auf Grundlage des Patents.
Die ersten Analysen des T-105 ergaben das das anfänglich gleichzeitige Einschalten
aller fünf Rauschgeneratoren über ein Nockenschaltkontakt dazu führte
das die Verteilung der erzeugten Zufallszahlen extrem Schlecht war und es zu vielen
Wiederholungen kam.
Es wurde daraufhin fünf Relais über den Nockenkontakt geschalten.
Die bedingt durch Fertigungstoleranzen die Rauschgeneratoren zu besseren Ergebnissen
führte.

Abb. 2: Rauschgenerator der endgültigen Fassung mit diversen Änderungen
gegenüber der Abb. 1.
Die Überprüfung der erzeugten Zufallsfolgen wurde mit dem Programm
P 620 und GAMMA 10 realisiert.
Rauschgenerator T-106
Bedingte Freigabe für die Produktion wegen fehlender Auswertung der Zufallsfolgen.
Rauschgenerator T-107
Freigabe für die Produktion ab 1967.
Rauschgenerator T-108
Keine Freigabe für die Produktion wegen schlechter Zufallsfolgen
Rauschgenerator T-109
Freigabe für die Produktion ab 1967.
Rauschgenerator T-110
Keine Freigabe für die Produktion wegen schlechter Zufallsfolgen.
Rauschgenerator T-111
Keine Freigabe für die Produktion wegen schlechter Zufallsfolgen.
Rauschgenerator T-113
Ist ein Rauschgenerator mit Anbindung an ein Mikro-
rechnersystem unter Verwendung der U-880 CPU.
Die T-113 erzeugt im Start-Stopp-Betrieb 8bit-Zufallsfolgen zur
Bildung von Schlüsselunterlagen des Typs 618, 758 und 821.
Rauschgenerator T-150
Rauschgenerator mit Stanzeinrichtung für 5 Kanal-Lochstreifen.
Es wurden Schlüsselmittel in Ziffern- oder Buchstabenausgabe
erzeugt. Es wurde auf der Basis des Reichert-Gerät
der
Firma Willi Reichert Elektronik PG 5605 entlehnt.
Rauschgenerator T-151
Der Rauschgenerator T-151 diente zum Erzeugen von Schlüssellochstreifen
für die Chiffriergeräte: CM-2, T-301
sowie zur Erzeugung von Kenngruppenheften für die Chiffriergeräte
M-125 FIALKA und M-105 AGAT.
Gebaut wurde es durch den VEB Steremat Berlin, ab 1969.

Abb.: Prinzipschaltbild T-151
Beschreibung des Schlüsselaufbaus für die CM-2 und T-301
Ein fortlaufender Lochstreifen wird mit Fernschreibzeichen ITA-2 gestanzt
das alle Kombinationen enthält außer:
V, E, X, ≡, Bu, 32te und es dürfen nicht 5 mal -
auftreten.
Beschreibung des Schlüsselaufbaus für Buchstabenlochstreifen
Der Schlüssellochstreifen enthält alle 26 Buchstaben - Fernschreibzeichen des ITA-2.
Beschreibung des Schlüsselaufbaus für Ziffernlochstreifen
Der Schlüssellochstreifen enthält alle 10 Ziffern - Fernschreibzeichen des ITA-2.
Es darf 5 mal -
nicht auftreten.

Abb.: Stromlaufplan des Rauschgenerators T-151
Rauschgenerator T-153
Rauschgenerator mit Stanzeinrichtung für 5 Kanal-Lochstreifen.
Es wurden Schlüsselmittel in Ziffern- oder Buchstabenausgabe
erzeugt.
T-200 Schreib- und Zählmaschine
Zählen der geschrieben Informationen, für die Prüfung
der Qualität von Schlüsselunterlagen.
T-202 Kombinator und Vergleicher
Der Kombinator bildet aus zwei Information mittels XOR ein Ergebnis,
das wiederum im Vergleicher geprüft wird.
Es können Lochstreifen von 5 bis 8 Kanal-Lochstreifen eingelesen
werden.
Es diente der automatischen Kryptoanalyse von chiffrierten Texten.
Als Halbleiter wurden OC872, 828 und OA 685C verwendet.
T-203 Schreibautomat
Die T-203 ist ein Schreibautomat für die Schlüsselmittelproduktion,
nach dem Vorbild der IBM 73.
T-251 Nebeneinanderschreiben
Schreibmaschine zum Nebeneinanderschreiben von Informationen aus 3 Lochkarten.
Das Nebeneinanderschreiben von Informationen die von 3 Lochkarten
parallel gelesen wurden. Erzeugung von Schlüsselunterlagen und
zur Prüfung insbesondere der Kryptoanalyse.
T-253 Streifenschreibmaschine
Die T-253 Streifenschreibmaschine enspricht der T-51 Fernschreibmaschine
- Streifenschreiber. Wurde ca 1965 geplant, wegen Unwirtschaftlichkeit
nicht realisiert.
T-601 Netzteil
Die T-601 ist ein Netzteil auf der Grundlage von Thyristoren, anstatt
Quecksilber-Thyratrons. Es ersetzte das Netzteil für Lochkarten der
Tabelliermaschine 402.
T-602 Vergleicher
Die T-602 vergleicht 5-Kanal-Lochstreifen die mit zwei T-53,
Fernschreibmaschinen-Lochstreifenleser, eingelesen wurde.
Die Lochstreifen wurden mit dem Gerät T-102 erzeugt.
T-603 Modul-Prüfgerät
Das Prüfgerät T-603 dient der Prüfung von URS-Modulen.
T-814 Aufspuleinrichtung
Die Aufgabe der T-814 das Aufspulen von bedruckten A4-Papier sowie
5-Kanal Lochstreifenpapier. Die Fernschreibmaschine T-51 ist das
Druckwerk.
T-815 Papierschneide- und Aufspuleinrichtung
Die Aufgabe T-815 ist das automatisierte Abschneiden von
A4-Endlospapierabschnitten sowie das Aufspulen von bedruckten A4-Papier.
Erzeugt durch eine Fernschreibmaschine T-51.
Die T-814 und T-815 wurde erbaut vom VEB Radebeuler Maschinenfabrik PLANETA.
T-817 Querschneideeinrichtung
Die Ausgabe der T-51, A4 Papier, wurde durch die T-817 zurechtgeschnitten.
M-10 Lochstreifenduplizierer (10fach)
Der Lochstreifenduplizierer dient zum Stanzen von 10 Lochstreifen.
Die Eingabe erfolgt über den Lochstreifenleser oder über den
elektrischen Anschluß eines Rauschgenerators oder anderer Geräte
wie CM-1, CM-2 oder M-130.
Dieses Gerät ermöglicht die schnelle Duplizierung von zirkularen Sprüchen
und Schlüsselunterlagen.
Eine Besonderheit ist das über 5 Stanzwerke 10 Lochstreifen gestanzt werden.

Abb.: 10fach Lochstreifenduplizierer M-10, Sammler *76

Abb.: Detail Lochstreifenleser, *76
Vertrauliche Verschlußsache
MfS 076/5432/62
Pflichtenfestlegung für den Umbau von Programmiergeräten
1. An das Programmiergerät werden zusätzlich folgende
Forderungen gestellt, die in aufgeführter Reihen-
folge stufenweise zu realisieren sind:
1.1. Von einem Lochstreifen, der alle 32 Lochkombinationen
des Internationalen Telegrafenalphabets Nr. 2 ( ITA )
enthalten kann, sollen hergestellt werden:
1.1.1. Bei der Betriebsart "Ziffern von 0 bis 9 programmiert"
1.1.1.1. Lochstreifen, die nur den Ziffern entsprechende Loch-
kombinationen enthalten. Die Anordnung dieser Loch-
kombinationen im Ausgangsstreifen soll den Anordnungen
der Lochkombinationen im Eingangsstreifen gemäß dem
für das Programmiergerät geltenden Umsetzungsschlüs-
sel von 32 Lochkombinationen auf 10 Lochkombinationen
(Ziffern) entsprechen.
1.1.1.2. Lochstreifen, die nur den Ziffern entsprechende Loch-
kombinationen enthalten und die Lochkombinationen für
"Zwischenraum", "Wagenrücklauf" und "Zeilenvorschub".
Die Verteilung dieser Lochkombinationen im Ausgangs-
streifen muß so programmiert werden können, daß von
jeder beliebigen Stelle ab jede dieser Lochkombina-
tionen t.beliebig oft eingeblendet werden kann. Die
Anordnung entsprechender Lochkombinationen im Ein-
und Ausgangsstreifen erfolgt so wie in 1.1.1.1.
1.1.2. Bei dar Betriebsart "26 Buchstaben programmiert"
1.1.2.1. Lochstreifen, die nur den 26 Buchstaben des deutschen
Normalalphabets entsprechende Lochkombinationen ent-
halten. Im Ein-und Ausgangsstreifen besteht die glei-
che Anordnung der den Buchstaben entsprechenden Loch-
kombinationen.
1.1.2.2. Lochstreifen, die nur den 26 Buchstaben entsprechende
Lochkombinationen und die Lochkombinationen für
"Zwischenraum", "Wagenrücklauf" und "Zeilenvorschub"
enthalten. Die Verteilung dieser Steuerkombinationen
muß wie in 1.1.1.2. und die Anordnung der den Buchsta-
ben entsprechenden Lochkombinationen wie in 1.1.2.1.
erfolgen.
1.1.3. Bei der Betriebsart "CM-2 programmiert"
Lochstreifen, die nur 25 verschiedenen Buchstaben ent-
sprechende Lochkombinationen und die Lochkombination
für "Wagenrücklauf" enthalten. Die Anordnung dieser
Lochkombinationen im Ausgangsstreifen muß wie in
1.1.2.1. erfolgen.
Von einem Lochstreifen, der alle 32 verschiedene Loch-
kombinationen enthält, sind die 28. LK (Ze), die 29.
LK (Bu), die 30. LK (Zi), die 31.LK (Zw), die 32. LK
und je nach der optimalsten technischen Realisierbar-
keit entweder die 24. LK (x) oder die 1. LK (A) zu
überlesen.
1.2. Bei jeder Betriebsart soll es möglich sein, zwei
identisch gleiche Lochstreifen herzustellen. Auf
jeden dieser beiden Lochstreifen muß nach einer
festgelegten Anzahl von Lochkombinationen eine Nummer
und eine Einlegemarkierung aufgedruckt werden können.
Diese Funktion muß abschaltbar sein.
Für die Realisierung sind etwa nachstehende Möglich-
keiten zu beachten:
1.2.1. Den Streifenlocher für das Programmiergerät durch
ein Stanzwerk mit Doppelstreifenlochung zu ersetzen
und ein entsprechendes Zähl- und Druckwerk anzu-
bringen oder
1.2.2. vom Programmiergerät direkt einen vorhandenen Doppel-
streifenlocher anzusteuern.
1.3. Nach einer vorher gewählten oder durch einen Programm-
streifen gesteuerten Anzahl von Lochkombinationen muß
im Falle 1.1.1. und 1.1.2. eine fortlaufende Numerie-
rung einblendbar sein. Diese muß wahlweise durch ein-,
zwei-und dreistellige Zifferngruppen erfolgen können
und in den Ausgangsstreifen eingelocht werden.
2. In Perspektive ist ein Programmiergerät so umzubauen,
daß folgende Funktionen ausgeführt werden können:
2.1. Von jeder beliebigen Stelle ab sollen innerhalb eines
Lochstreifens, der bis zu 32 verschiedene Lochkombi-
nationen enthalten kann, beliebige Lochkombinationen
oder Gruppen von Lochkombinationen eingeblendet werden
können. Diese Einblendung muß auf zwei Arten möglich
sein:
2.1.1. Steuerung durch einen Programmstreifen
2.1.2. Steuerung durch bestimmte im Eingangsstreifen ent-
haltene Lochkombinationen, die vorwählbar getastet
oder gesteckt werden können, wobei alle möglichen
32 Lochkombinationen des ITA gleichberechtigt vor-
wählbar sein müssen.
2.1.3. Beispiel zu 2.1.1.
Der Eingangsstreifen möge alle 32 Lochkombinationen
des ITA enthalten. Nach beispielsweise je 20 Loch-
kombinationen des Eingangsstreifens soll in den Aus-
gangsstreifen eine bestimmte Gruppe von Lochkombi-
nationen eingeblendet werden.
Die Gruppe von Lochkombinationen befindet sich in
einem Programmstreifen. Während aus dem Programm-
streifen übernommen wird, muß der Eingangsstreifen
stoppen, und zwar so lange, bis aus dem Programm-
streifen das Signal kommt "Übernehme aus dem Ein-
gangsstreifen". Der Programmstreifen läuft während
der Übernahme aus dem Eingangsstreifen synchron mit,
bis aus dem Programmstreifen das Signal kommt: "Über-
nehme aus dem Programmstreifen". Außer diesen beiden
Übergangssignalen müssen alle möglichen Gruppen von
Lochkombinationen, die diese beiden nicht enthalten,
aus dem Programmstreifen übernommen werden können.
2.1.4. Beispiel zu 2.1.2.
Der Eingangsstreifen kann wieder alle 32 verschiedene
Lochkombinationen enthalten. Beispielsweise sei die
32. Lochkombination zur Einblendung vorgewählt worden.
Jedes mal, wenn im Eingangsstreifen die 32. Lochkom-
bination abgetastet und im Ausgangsstreifen eingelocht
worden ist, soll im Ausgangsstreifen eine Gruppe von
Lochkombinationen eingeblendet werden, z.B. 5-mal Bu-
Umschaltung oder Bu, a, b, c, d, e.
Diese Gruppen von Lochkombinationen werden aus einem
Programmstreifen entnommen. Jedesmal, wenn im Ein-
gangsstreifen die vorgewählte Lochkombination er-
scheint, bleibt der Eingangsstreifen stehen und löst
gleichzeitig den Start des Programmstreifens aus.
Ist aus dem Programmstreifen die gewünschte Loch-
kombination übernommen worden, wird durch ein Signal
im Programmstreifen der Stopp desselben ausgelöst
und es erfolgt der Start des Eingangsstreifens.
2.2. Überlesen und Austauschen
2.2.1. Überlesen von Lochkombinationen im Eingangsstreifen
Unter Überlesen soll verstanden werden, daß Lochkom-
binationen im Eingangsstreifen unterdrückt werden
und im Übergangsstreifen dafür keinerlei Markierung
erscheint.
Es soll möglich sein, Gruppen von Lochkombinationen
von vorgewählter Länge zu überlesen.
Es ist eine wahlweise Einteilung des Ausgangsstrei-
fens in Zweier-, Dreier-, Vierer- und Fünfergruppen
vorzusehen.
Als Teilungskombination muß dann eine im Ausgangs-
streifen nicht enthaltene Lochkombination dienen
können. Die Teilung muß abschaltbar sein.
2.2.2. Austauschen von Lochkombinationen oder Gruppen von Loch-
kombinationen gegen andere
Unter Austauschen soll verstanden werden, daß vorwähl-
bare Lochkombinationen oder Gruppen von Lochkombina-
tionen gegen andere ausgetauscht werden.
So soll im Eingangsstreifen, der alle 32 verschiedene
Lochkombinationen enthalten kann, beispielsweise ein
vorgewähltes Polygramm der Länge k ≤ 20 gegen ein
Polygramm der Länge m ≤ 20, bestehend aus den Loch-
kombinationen für Zwischenraum und Bu-Umschaltung,
ausgetauscht werden. Das geschieht so, daß im Eingangs-
streifen eine vorgewählte Gruppe von Lochkombinationen
der Länge k überlesen wird und dafür im Ausgangsstrei-
fen eine bestimmte andere Gruppe von Lochkombinationen
der Länge m aus einem Programmstreifen eingeblendet
wird. Die Steuerung der Ein-und Ausgangsstreifen
könnte etwa sinngemäß wie in 2.1.4. erfolgen.
Es ist die Möglichkeit zu prüfen, wieviele verschie-
dene Gruppen von Lochkombinationen etwa bis zur Länge
k = 20 gleichzeitig gegen andere ausgetauscht werden
könnten. Eine Teilung des Ausgangsstreifens ist
ebenso wie in 2.2.1. vorzusehen.
Als Minimalforderung wird erhoben, daß jede Loch-
kombination des ITA unabhängig von jeder anderen
gegen jede andere ausgetauscht werden kann. So muß
sich z.B. die 32. Lochkombination durch jede andere
der noch verbleibenden 31 ersetzen lassen.
Kostenstelle 214 Berlin, den 18. 12. 1962
Pei./
Aktennotiz
Besprechung über Änderung der Anlage I 400 am 8. 12. 1962
Thema: Änderung der Anlage I 400, damit Lochstreifen
für den T 301-Betrieb hergestellt werden können.
1. Es wurde festgelegt, die Änderung im Gerät I 401 durchzuführen.
Es wird die Funktion 1 x W 26 für den T 301-Betrieb hergerichtet.
2. Die Funktion, wird nicht umschaltbar ausgeführt, da auch in
absehbarer Zeit keine Geräte eingesetzt werden, die Buchstaben-
streifen als Zirkulare benötigen. Reine Buchstabenstreifen wer-
den nur in einfacher Ausfertigung benötigt und können deshalb
auch mit den Geräten I 409 aus Streifen, die alle 32 Kombina-
tionen enthalten, hergestellt werden.
3. Es wird der Buchstabe "A" ausgeblendet.
4. Umfang der Änderung:
Die Leitung des Ruhekontaktes 90-3 (Anschluß 11) wird auf den
Arbeitskontakt 90-1 gelegt. Die geänderten Unterlagen werden
der Kst. 810 nach Fertigstellung nachgereicht.
5. Die Änderung wird durch die Genossen der Kst. 810 ausgeführt.
6. Die Änderung im Gerät I 400 hat gegenüber einer Änderung im
Gerät I 409 den Vorteil, daß sofort entweder ein Streifenpaar
für individuellen Betrieb oder ein Zirkular bis Z = 20 herge-
stellt werden kann
( P e i s e r )
B e r i c h t
über die Realisierung des OT-Auftrages 2.214.02.662
( T 150 )
1. Einleitung
Von der Abteilung XI wird
- für die Analyse von eigenen und fremden Chiffrier-
verfahren,
- für die Herstellung von speziellen Chiffriermitteln,
(z. B. Mischalphabeten),
- für die Herstellung von Geheimtexten für die Dekryp-
tierungszwecke und
- für die Herstellung von Lochstreifen mit speziellem
Informationsinhalt zur weiteren Verarbeitung auf
Spezialmaschinen
ein Gerät benötigt, das
- programmierte Lochstreifen nach dem Internationalen
Telegraphen-Alphabet Nr. 2 (ITA) herstellt,
- aus 31 Lochstreifen nach einem Programm Informationen
übernimmt,
- durch ein Programm festgelegte Kombinationen
ausblendet oder durch andere ersetzt,
- Lochstreifen miteinander vergleicht, und
- Lochstreifen auf Folgen vorwählbarer Länge m (m = 1 ... 8)
kontrolliert.
Eine detaillierte Pflichtenfestlegung ist im vorläufigen
Pflichtenheft der Abteilung XI niedergelegt.
2. Lösungsmöglichkeiten
Es bietet sich zwei grundsätzliche Lösungsmöglichkeiten an.
- Umentwicklung eines westdeutschen Gerätes unter teil-
weiser Verwendung westdeutscher Bauelemente,
- Neuentwicklung mit Verzicht auf Importbauelementen.
2.1. Lösungsvariante 1
Diese Lösungsvariante sieht die Umentwicklung und Er-
weiterung des Programmiergerätes PG 5605 der Fa. Reichert,
Trier, vor. Die Grundforderungen, wie sie auch im vor-
läufigem Pflichtenheft der Abteilung XI genannt werden,
werden von diesem Gerät erfüllt. Die vorhandenen Bau-
gruppen
- Stromversorgung,
- Locher,
- Ausblendschaltung,
- Betrieb-Halt-Schaltung
- Entschlüsselungsmatrix,
- Umschlüssler,
- Würfelstreifensender,
- Programmsender und
- Taktgeber
können voll und ganz herangezogen werden.
Die Forderung, daß die Betriebsarten
- 26 Buchstaben programmiert und
- Ziffern 0 - 9 programmiert
erhalten bleiben, wird erfüllt.
2.2. Lösungsvariante 2
Die Lösungsvariante sieht die vollkommene Neuentwicklung
des Gerätes vor, d. h. es wird nicht auf das Programmier-
gerät der Fa. Reichert und auch nicht auf die Einbau-
abtaster dieser Firma zurückgegriffen.
3. Arbeitsumfang
3.1. Realisierung der Lösungsvariante 1
Folgende Veränderungen müssen vorgenommen werden:
3.1.1. Umentwicklung des Programmsenders
Der Programmsender wird so verändert, daß er selbst
keine Informationen an den Locher überträgt. Er erhält
eine Auswerteschaltung mit 31 (32) Ausgängen.
Von diesen Ausgängen werden 31 Sender - 1 Primär - und
30 Sekundärsender (Lochstreifenleser) - angesteuert.
Bei Aufruf eines Senders gibt dieser die von ihm aus
dem einliegenden Lochstreifen abgetasteten Informationen
an den Locher ab.
Es ist zweckmäßig, das Gerät mit Sendern der gleichen
Bauart wie sie bereits in der Industrieausführung vor-
handen sind, zu erweitern. Dadurch ist eine einheitliche
Ansteuerung, Auswechselbarkeit der Sender, sowie eine
einheitliche weitere Auswertung der abgetasteten Infor-
mationen möglich.
Die Stromversorgung braucht trotz der zusätzlichen 30
Lochstreifenabtaster nicht erweitert werden.
3.1.2. Erweiterung des Umschlüßlers
Der Umschlüßler ist so zu erweitern, daß sämtliche
Zeichen (nicht nur die Ziffern 0 - 9) über den Um-
schlüßler geführt werden können.
3.1.3. Erweiterung der Entschlüsselungsmatrix
Zwischen Entschlüsselungsmatrix und dem Umschlüßler
ist eine Baueinheit einzufügen, die gestattet, einen
beliebigen Ausgang der Entschlüsselungsmatrix auf einen
beliebigen Eingang des Umschlüßlers zu schalten, bzw.
der Ausblendschaltung zuzuführen.
3.1.4. Entwicklung der Folgenkontrolleinrichtung
Die Folgenkontrolleinrichtung ist im Programmiergerät
der Fa. Reichert nicht enthalten, sie muß neu entwickelt
werden. Sie besteht aus einer mehrstufigen Transistor-
schaltung mit verschiedenen Ausgängen, an denen Zähler
angeschlossen sind. Diese Kontrolleinrichtung arbeitet
mit den Funktionsgruppen Locher, Ausblendschaltung,
Programmiersender und den 31 Sendern (1 Primär- und
30 Senkundärsendern) zusammen.
Diese Folgenkontrolleinrichtung wird auch für das Ent-
wicklungsthema T 151 und T 153 vorgesehen.
3.1.5. Streifenvergleich
Diese Betriebsart ist im Programmiergerät noch nicht
vorhanden. Sie muß neu entwickelt werden. Bei dieser
Schaltung handelt es sich um eine logische Transistor-
schaltung, die mit den Funktionsgruppen Locher, Programm-
sender, Sekundärsender, Umschlüßler und Betrieb-Halt-
Schaltung zusammenarbeitet.
3.2. Zusammenfassung der Lösungsvariante 1
Um Entwicklungszeit und Kosten zu sparen, wird beabsich-
tigt, ein handelsübliches Programmiergerät der Fa. Reich-
ert, Trier zu verwenden und zu erweitern. Dies hat den
Vorteil, daß ein großer Teil der Funktionsgruppen schon
vorliegt.
Als Leseköpfe sind zweckmäßigerweise die Einbau- Abtaster
der gleichen Firma zu verwenden. Dieser Kopf ist steck-
bar und dadurch auswechselbar. Er zeichnet sich durch
Verhältnismäßig kleines Volumen und leichtes Gewicht aus,
und befindet sich in einer gewissen Stückzahl bereits bei
der Abteilung XI in verschiedenen Geräten im Einsatz.
Gleichartige Abtastköpfe werden in der DDR nicht hergestellt.
Eine Entwicklung dieser Abtaster ist wegen der geringen
Stückzahlen aus wirtschaftlichen Gründen nicht zu vertreten.
Außerdem würde eine Eigenentwicklung wegen der notwendigen
Werkzeuge und Vorrichtungen sehr teuer und zeitraubend sein.
Folgende Kosten fallen bei dieser Variante an:
DM West: 1 Programmiergerät PG 5605 15 620 DM West
35 Einbau- Abtaster 21 35 34 720 " "
Spezialbauelemente 1 680 " "
52 000 DM West
‗‗‗‗‗‗‗‗‗‗‗‗‗‗
DM der Deutschen Notenbank
Bauelemente 5 000 DM
Entwicklungskosten (geschätzt) 60 000 DM
65 000 DM
‗‗‗‗‗‗‗‗‗
Es ist beabsichtigt, die Entwicklung in der volkseigenen
Industrie durchführen zu lassen.
Geplanter Entwicklungsbeginn: Anfang III/64.
4. Neuentwicklung
Eine Neuentwicklung ist wegen des hohen Anteils an mecha-
nischen Baugruppen - Locher, - Einbauabtaster, - Taktgeber
(nockengesteuert) - und der damit verbundenen hohen Werk-
zeugkosten bzw. langen Entwicklungszeiten nicht zu empfehlen.
Außerdem würden die Entwicklungskosten erheblich höher sein.
Für die Kostenstelle 214:
Fickenwirth Peiser
Für die Abteilung XI:
Stephan Bürger
gesehen:
Schürrmann Baruth
Geheime Verschlußsache
MfS 006/139/64
Programmiergerät
1.) Allgemeines
Das Programmiergerät dient zur Herstellung programmierter
Lochstreifen. Das Programmiergerät ist im wesentlichen mit
2 Lochstreifenlesern und einem, durch ein Verbindungskabel
an das Gerät angeschlossenen Streifenlocher ausgerüstet.
Vom ersten Lochstreifenleser wird der Programmstreifen
(Lochstreifen 1) gelesen, von dem zweiten Leser der Lochstrei-
fen 2, in dem alle 32 Kombinationen des Internationalen Tele-
grafenalphabetes Nr. 2 (ITA Nr. 2) enthalten sein können.
Im Programmstreifen sind die Zeichen Wagenrücklauf, Zwischen-
raum, Zeilenvorschub und das Zeichen "Z" in einer gewünschten
Reihenfolge enthalten, d.h. dieser Streifen muß vor Inbetrieb-
nahme des Gerätes hergestellt werden. Die vom Progrmmnstreifen-
Leser gelesenen Zeichen "WR, ZW und ZL" werden dem Streifen-
locher zugeführt und abgelocht. Liest der Programmstreifen-
leser das Zeichen "Z", dann werden dem Streifenlocher vom
Leser 2 gelesene Zeichen so zugeführt, wie es in den 2 mög-
lichen Betriebsarten des Programmiergerätes im folgenden näher
beschrieben ist.
Zur Registrierung der in dem programmierten Lochstreifen ent-
haltenen Zeichen kann ein Zeichenzählgerät an das Programmier-
gerät angeschlossen werden. Die Arbeitsgeschwindigkeit des
Programmiergerätes beträgt ca. 10 Zeichen pro Sekunde. Durch
das Ausblenden einiger Zeichen kann die Geschwindigkeit zeit-
weilig auf 8 Zeichen pro Sekunde reduziert werden.
Betriebsart "26 Buchstaben programmiert"
Es wird ein programmierter Lochstreifen hergestellt, in dem
die Zeichen Wagenrücklauf, Zwischenraum und Zeilenvorschub,
sowie die Zeichen A-Z (26 Zeichen) in einer von Lochstreifen
1 und 2 abhängigen Reihenfolge enthalten sind.
Die im Programmstreifen enthaltenen Zeichen "WR, ZW, ZL"
werden dem Streifenlocher zugeführt und abgelocht. Liest der
Programmstreifen-Leser das Zeichen "Z", dann werden die im
Leser 2 vorliegenden Zeichen von einer Relaispyramide ausge-
wertet. Von dieser werden die Zeichen Buchstabenwechsel, Zif-
fernwechsel, Zeilenvorschub, Zwischenraum, Wagenrücklauf und
das 32. Zeichen (Leerzeichen) unterdrückt, d. h. diese Zei-
chen werden vom Streifenlocher nicht abgelocht und vom Zei-
chenzählgerät nicht registriert. Die übrigen 26 Zeichen (A-Z)
werden in der im Streifen 2 vorliegenden Reihenfolge dem
Streifenlocher zugeführt und. abgelocht. Das angeschlossene
Zeichenzählgerät registriert alle im programmierten Loch-
streifen abgelochten Zeichen.
Betriebsart "Ziffern 0-9 programmiert"
Es wird ein programmierter Lochstreifen hergestellt, in dem
die Zeichen "Wagenrücklauf, Zwischenraum und Zeilenvorschub"
sowie die Ziffern 0-9 in einer vom Lochstreifen 1 und 2 ab-
hängigen Reihenfolge enthalten sind. Die Zeichen "WR, ZW und
ZL" werden wie bei Funktion "26 Buchstaben programmiert" aus
dem Programmstreifen vom Streifenlocher übernommen.
Liest der Programmstreifenleser das Zeichen "Z", dann werden
die im Leser 2 vorliegenden Zeichen von der Relaispyramide
ausgewertet. Die Zeichen "Buchstabenwechsel" und das 32.Zeichen
werden unterdrückt. Die restlichen 30 Zeichen des Streifens 2
werden von der Relaispyramide in 10 Gruppen zu je 3 Zeichen
aufgeteilt und einem Umschlüssler für die Ziffern 0-9 des
5-er Code zugeführt. Aus diesem Umschlüssler werden die Zif-
fern 0-9 vom Streifenlocher übernommen und abgelocht. Das
Zeichenzählgerät registriert alle im programmierten Streifen
enthaltenen Zeichen.
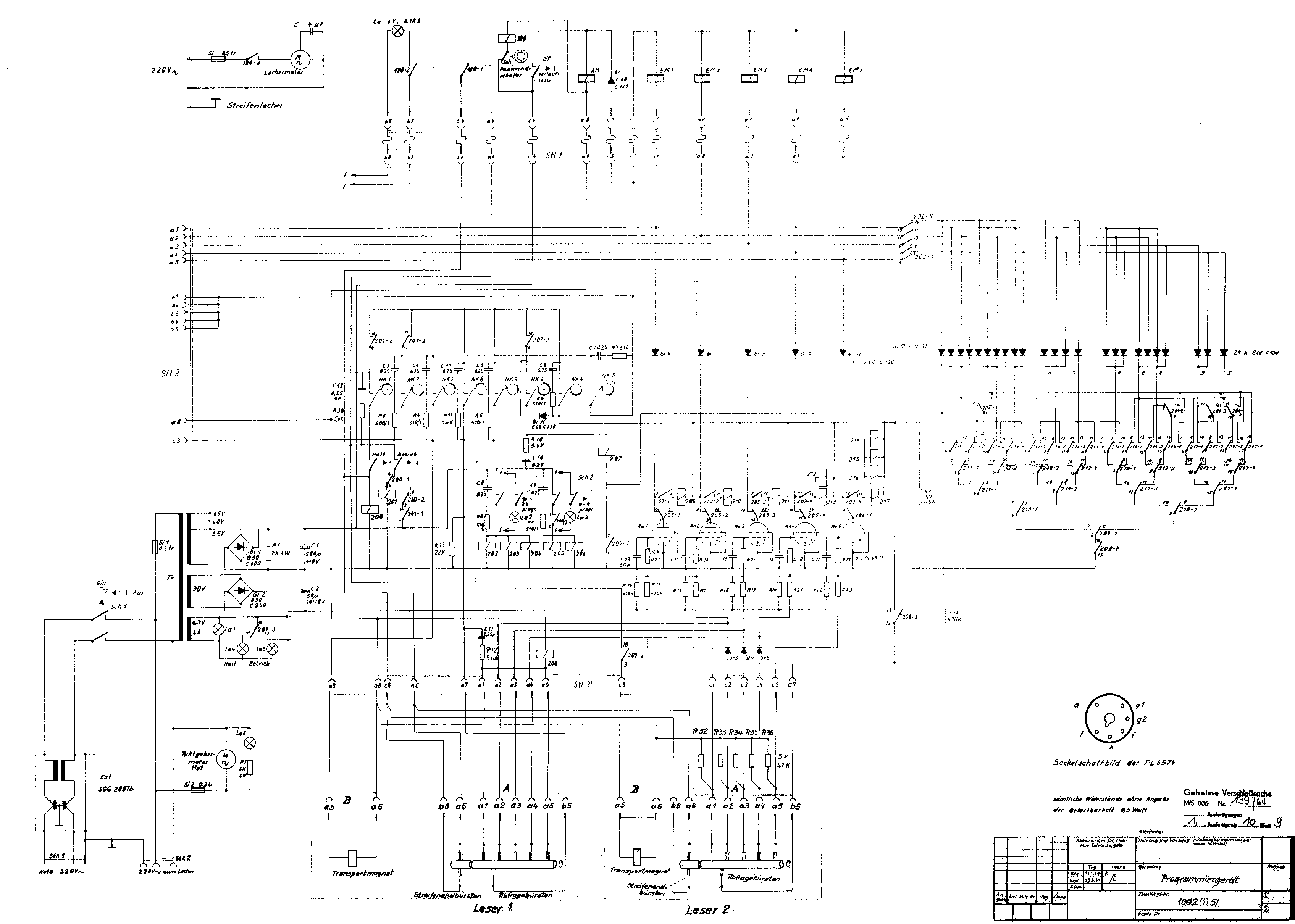
2.) Technische Beschreibung
a) Aufbau
Das Programmiergerät ist in einem Gehäuse montiert, das
mit seitlichen, umklappbaren Transportgriffen versehen
ist. Auf der Deckplatte des Gehäuses sind zwei Einbau-
Lochstreifen-Leser, eine Abwickeltrommel für den Loch-
streifen 2 und ein Teleskop-Streifenhalter für den Pro-
grammstreifen angebracht. Die max. Länge des Programm-
streifens kann bei voll ausgezogenem Teleskop-Streifen
halter ca. 2,2 m betragen.
Auf der Frontplatte des Einschubes sind die Bedienungs-
elemente, wie Netzschalter, Betrieb-Halt-Tasten, Funktions-
wahlschalter, Sicherungen und Kontrollampen montiert. Das
Chassis des Einschubs vereinigt das Netzteil, ein Entstör-
gerät, einen motorgetriebenen Taktgeber mit 8 Nockenkon-
takten, 5 Thyratronröhren PL 6574, eine aus 9 Kammrelais
aufgebaute Kontakt-Pyramide mit 32 Ausgängen, einen Sperr-
zellen-Umschlüssler, Umschaltrelais udgl. An der Rückseite
des Gerätes befinden sich vier Anschlußbuchsen für den
Netzeingang, den Netzausgang und Steueranschluß zum Strei-
fenlocher und zum Zeichenzählgerät.
b) Betrieb-Halt-Schaltung
Die Frequenz, Folge und Dauer der elektrischen Vorgänge
im Programmiergerät ist durch 8 Nockenkontakte, die von
einem Getriebemotor getrieben werden, bestimmt. Zur Ver-
meidung von Fehlfunktionen bei Starten und Stoppen des
Gerätes dient eine Betrieb-Halt-Schaltung, die sich haupt-
sächlich aus dem Nockenkontakt NK 1 (65° - 120°), den
Tasten "Betrieb" und "Halt", sowie den Relais 200 und
201 zusammensetzt. Bei Betätigen der Taste "Betrieb" wird
Rel. 201 über NK 1 und Rel. - Kont. 200-1 erregt und hält
sich über Kontakte 200-2 und 201-1 selbst. Kontakt 201-2
schließt den Speisestromkreis der Einstellmagnete und des
Auslösemagnets des Streifenlochers, der Transportmagnete
der Lochstreifenleser 1 und 2, der Zeichenausblendung und
der Zählerregung im Zeichenzählgerät. Bei Betätigen der
Taste "Halt" wird Rel. 200 über NK 1 erregt. Kontakt 200-2
öffnet den Selbsthalte-Stromkreis vom Rel. 201 und dieses
fällt ab. Kontakt 200-1 öffnet und verhindert eine Erregung
von Rel. 201, solange Rel. 200 erregt ist. Kontakt 201-2
öffnet den Speisestromkreis für die bereits angeführten
Elemente.
Eine Erregung von Rel. 200, d.h. Stoppen des Programmier-
gerätes, kann auch durch Schließen der Streifenendkontakte
der Lochstreifenleser 1 und 2 und durch Schließen von Kon-
takt 190-1 des Streifenendrelais 190 im Streifenlocher er-
folgen.
c) Betriebsart "26 Buchstaben programmiert"
Die Relais 202, 203 und 204 werden bei Betätigen der Taste
"26 Progr." erregt. Die Kontakte 202-1 bis 202-5 trennen
den Umschlüssler, der aus den Sperrzellen Gr 12 - Gr 35
aufgebaut ist, von den Einstellmagneten des Streifenlochers.
Die Kontakte 203-1 bis 203-5 verbinden die Relais 209 - 216
mit den fünf Einstellmagneten des Streifenlochers.
Die Kontakte 205-1 bis 205-4 und 206-1 sind in Ruhelage
(durch gegenseitige Auslösung mit Taste "26 progr." ist
Taste "0 - 9 progr." geöffnet und Rel. 205 und 206 nicht
erregt,) und so die Anoden der Thyratronröhren Rö 1 Rö 5
(PL 6574) mit den Einstellmagneten des Streifenlochers
verbunden. Die Kontakte 204-1 bis 204-4 schalten die
Pyramidenausgänge der Zeichen "Ziffernwechsel, Zeilenvor-
schub, Zwischenraum und Wagenrücklauf" der Zeichenaus-
blend-Schaltung zu. Wird z.B. vom Programmstreifenleser
das Zeichen "Zeilenvorschub" (Kanal 2) gelesen, dann
ist Abfragekontakt 2 geschlossen und über diesen bei
Schließen von NK 8 (75° - 360°) dem Zündgitter des Thy-
ratrons Rö 2 eine positive Spannung zugeführt. Rel. 208
ist nicht erregt (Abfragekontakt 1 u. 5 des Programm-
streifenlesers sind geöffnet). Kontakt 208-2 ist geöffnet,
so daß der Leser 2 keinen Transportimpuls erhält. Kontakt
208-3 ist geöffnet, so daß den Thyratronröhren über die
Abfragebürsten des Lesers 2 kein Zündimpuls zugeleitet
werden kann. Kontakt 208-4 ist geöffnet und trennt die
Kontaktpyramide von der Ausblendschaltung. Bei 120° Nocken-
wellensteilung (NWS) (siehe Nockenzeitdiagramm 1003 )
zündet Thyratron 2 durch Schließen von NK 4, Rel. 210
wird erregt, Kontakte 210-1 und 210-2 sind in Arbeits-
stellung und stellen die Pyramide auf das Zeichen Zeilen-
vorschub ein.
Kontakt 208-4 ist jedoch, wie bereits oben erläutert, ge-
öffnet, so daß eine Erregung des Ausblendrelais 207 nicht
erfolgen kann und Kontakt 207-3 in Ruhelage bleibt.
Somit werden der Einstellmagnet EM 2 und der Auslösemag-
net AM des Streifenlochers bei 190° NWS über NK 5 erregt.
Das Zeichen "Zeilenvorschub" wird abgelocht. Parallel
zum Einstellmagnet EM 2 wird Rel. 148 im Zeichenzählgerät
erregt. Die Pyramide ist dann für Zähler 28 eingestellt,
und dieser erhält bei Schließen von NK 7 einen Fortschalt-
impuls. In gleicher Weise werden die vom Programmstreifen-
leser gesendeten Zeichen: "Zwischenraum und Wagenrücklauf"
vom Streifenlocher abgelocht und vom Zeichenzählgerät re-
gistriert. Liest der Programmstreifenleser das Zeichen "Z"
(Kanal 1 u. 5) dann ist Rel. 208 bei Schließen von NK 8
erregt. Kontakt 208-3 ist geschlossen, so daß jetzt die
Zündimpulse über die Abfragebürsten des Lesers 2 abhängig
vom vorliegenden Zeichen den Thyratronröhren zugeführt
werden. Kontakt 208-4 ist geschlossen und somit die Kon-
taktpyramide zur Ausblendung von 6 Zeichen vorbereitet.
Liest der Leser 2 z.B. das Zeichen "Buchstabenwechsel",
ein Zeichen, das ausgeblendet werden soll (1,2,3,4,5),
zünden bei Schließen von NK 4 alle Thyratronröhren und
die Rel. 209 - 217 sind erregt. Die Kontaktpyramide wird
eingestellt und das Rel. 207 bei Schließen von NK 6 erregt.
Folgender Stromkreis: (+) 70V - NK 4 - Gr 11 - NK 6 -
Rel. 207 - Kont. 214-1 Kont. 212-1 - Kont. 211-1 - Kont.
201-1 - Kont. 209-1 Kont. 208-4 -(-) 70 V. Rel. 207 hält
sich über Kontakte 207-1 und 207-2 selbst. Kontakt 207-3
öffnet, so daß Streifenlocher, Zeichenzählgerät und der
Transportmagnet das Programmstreifenlesers keine Erreger-
impulse erhalten. Der Leser 2 erhält bei Schließen von
NK 3 (Kontakt 208-2 ist geschlossen) einen Transportim-
puls, so daß das nächste Zeichen im folgenden Umlauf ab-
gefragt werden kann. NK 6 öffnet bei 750 NWS und Rel.
207 fällt ab. In gleicher Weise erfolgt die Ausblendung
der Zeichen "Zi, WR, ZL, ZW u. 32. Zeichen" , wenn diese
vom Leser 2 gelesen werden.
Rel. 207 wird nicht erregt, wenn die Zeichen A-Z vom
Leser 2 abgefragt werden. Kontakt 207--3 bleibt geschlos-
sen und diese Zeichen werden abgelocht und vom Zeichen-
zählgerät registriert.
d) Betriebsart: "Ziffern 0-9 programmiert"
Taste "0-9 prog." ist gedrückt und Taste "26 progr."
durch gegenseitige Auslösung geöffnet. Die Rel. 202,
203 und 204 sind nicht erregt. Die Kontakte 202-1 bis
202-5 verbinden die Einstellmagnete des Lochers mit
dem Sperrzellenumschlüssler. Kontakte 203-1 bis 203-5
sind geöffnet und somit die Einstellmagnete von den
Pyramiden - Rel. 209-217 getrennt. Kontakte 204-1 bis
204-4 trennen die Pyramidenausgänge der Zeichen "Zi, ZL,
ZW und WR" von der Ausblendschaltung und schalten diese
Ausgänge jeweils 2 anderen Ausgängen der Pyramide zu,
so daß 30 Ausgänge der Pyramide in 10 Gruppen mit jeweils
3 parallelgeschalteten Pyramidenausgängen zusammengefaßt
sind. Diese Gruppen sind mit dem Sperrzellen-Umschlüssler
verbunden. Die vom Programmstreifenleser abgetasteten
Zeichen "ZW, ZL und WR" werden wie bei Betriebsart "26
prog." vom Streifenlocher abgelocht und vom Zeichenzähl-
gerät registriert. Kontakt 208-1 ist dann geöffnet, die
Rel. 205 und 206 nicht erregt und deren Kontakte 205-1
bis 205-4 und 206-1 in Ruhelage. Die Einstellmagnete des
Lochers sind so den Thyratronröhren zugeschaltet. Kontakt
208-4 ist geöffnet und es erfolgt keine Ausblendung.
Eine Erregung der Einstellmagnete über den Sperrzellenum-
schlüssler und die Kontaktpyramide ist dann nicht möglich.
Liest der Programmstreifenleser das Zeichen "Z" (Kanal 1
u. 5), dann ist Rel. 208 erregt und dessen Kontakte in
Arbeitsstellung. Die Rel. 205 und 206 sind über Kontakte
208-1 erregt, deren Kontakte in Arbeitsstellung und somit
die Einstellmagnete des Lochers von den Thyratronröhren
getrennt und diesen Röhren die Pyramidenrelais 209-217
zugeschaltet.
Das vom Leser 2 gelesene Zeichen stellt die Kontaktpyra-
mide ein. Die Pyramidenausgänge der Zeichen: "Buchstaben-
wechsel und 32. Zeichen" sind in der Ausblendschaltung
verblieben. Diese Zeichen werden unterdrückt. Tastet der
Leser 2 z.B. das Zeichen "A" (Kanal 1 und 2) ab, dann
sind die Pyramidenrelais 209 und 210 bei Schließen von
NK 4 durch Zünden der Röhren 1 und 2 erregt. Die Pyramide
wird eingestellt und bei Schließen von NK 5 ergibt sich
folgender Stromkreis: für die Einstellmagnete 1, 2 und 5
des Streifenlochers: (+) 70 V-Kont. 201-2 - Kont. 207-3
- NK 5 - EM 1,2,5 - Gr 19,20,21 - Kont. 214-4 - Kont. 212
-2Kont. 211-1 - Kont. 210-1 - Kont. 209-1 - Kont. 208-4
(-) 70 V. Es wird demnach das Zeichen der Ziffer 2 abge-
locht, was ebenso geschieht, wenn die Zeichen "W" (Ka-
nal 1, 2 u. 5.) und das "X" (Kanal 1,3, 4 u. 5) vom Leser
2 abgetastet werden. Die Zuordnung der übrigen 9 Gruppen
zu den restlichen Ziffern ist aus dem Schaltbild und
einer diesen Unterlagen beigefügten Tabelle ersichtlich.
Alle im programmierten Ausgangsstreifen enthaltenen Zei-
chen werden wie bei Betriebsart "26 progr." vom Streifen-
locher abgelocht und vom Zeichenzählgerät registriert.
3.) Bedienungsanweisung
Den Streifenlocher und das Zeichenzählgerät an das Pro-
grammiergerät anschließen. Auf die Streifenvorratstrommel
des Lochers eine Streifenrolle auflegen und den Abtasthe-
bel des Papierendschalters in Arbeitsstellung bringen.
Netzschalter im Programmiergerät einschalten. Den Streifen
in den Papierkanal des Lochers einführen. Die Pappierklappe
aufdrücken, den Streifen unter der Klappe durchführen und
die Papierklappe wieder zuschnappen lassen. Die Taste "Vor-
lauf" solange drücken, bis ein genügend langer Streifen zur
Befestigung in der Aufrolltrommel des Lochers vorgelaufen
ist. Den Programmstreifen, in dem die Zeichen "WR, ZL, ZW
und "Z" in einer gewünschten Reihenfolge enthalten sind,
in den Programmstreifenleser einlegen. Eine gelochte Strei-
fenrolle, in der alle Kombinationen des ITA Nr. 2 enthal-
ten sein können, auf die Vorratstrommel des Programmier-
gerätes auflegen und den Streifen in den Leser 2 einlegen.
Die gewünschte Betriebsart durch Drücken der Tasten "26
progr." oder "0-9 progr." im Programmiergerät einstellen.
Die Taste "Betrieb" drücken. Vom Streifenlocher wird ein
programmierter Lochstreifen der gewählten Betriebsart ent-
sprechend abgelocht. Ist der Streifen in der Vorratstrom-
mel des Programmiergerätes oder des Streifenlochers abge-
laufen, dann schließt der Papierendschalter des Lochers,
bzw. des Lesers 2 und stoppt das Programmiergerät. Das
Gerät ist dann auszuschalten, bzw. neue Streifen zur wei-
teren Inbetriebnahme aufzulegen. Die Klebestelle des als
endloses Band laufenden Programmstreifens ist sauber aus-
zuführen, damit Abfragefehler vermieden werden.

 | Edelgas-Thyratron | S 1,3/2 i V |
|---|
| electronic | |
|---|
Die S 1,3/2 iV ist eine edelgasgefüllte
Glühkatodenröhre mit Steuer- und
Schirmgitter. Sie wird vorwiegend für
Relaisschaltungen verwendet.
Diese Röhre entspricht den Typen ASG 6574,
CV 2253, EN 32, PL 6574 und 6574 und ist
den Typen B-2A und EN 33 ähnlich.
|  |
| Heizung | |  |
| Indirekt geheizte Oxidkathode |
| uf | | 6,3 V |
| If | ca. | 0,95 A |
| tA | ≥ | 15 s |
| Betriebswerte | |
| Ui | | 10 V | |
| Uz | | 40 V |
| (bei Ug1 = Ug2 = 0 V) |
| Grenzwerte | |
| -Uas | max | 1,3 kV |
| Uas | max | 0,65 kV |
| Iks | max | 2 A |
| -Ug1 s | max | 250 V*1 |
| -Ug1 s | max | 10 V*2 |
| Ig1 | max | 20 mA*3 |
| Rg1 | max | 10 MΩ*3 |
| (bei Ik = 20 mA) |
| -Ug2 s | max | 100 V*1 |
| -Ug2 s | max | 10 V*2 |
| Ig2 | max | 20 mA*4 |
| |
| Betriebslage: | | beliebig |
| Masse: | ca | 35 g |
| Sockel: | | 8-17 |
| TGL 200-8157, Bl. 2 |
| Röhrenstandard: | | TGL 12079 |
| Fassung: | 8-17 | TGL 14896 |
| |
| *1 | bei gelöschter Röhre. |
| *2 | bei gezündeter Röhre. |
| *3 | tint g1 max = 1 Periode |
| *4 | tint g2 max = 1 Periode |
 | VEB Werk für Fernsehelektronik 1/4.68 |
 | Grenzwerte |
| tint | max. | 15 s |
| U-f/k | max. | 100 V |
| U+f/k | max. | 25 V |
| +Tamb | max. | 90°C |
| -Tamb | max. | 75°C |
|
| Kapazitäten | |
| Ce | ca. | 2,5 pF |
| Ca | ca. | 3 pF |
| Cg1/a | ≤ | 0,35 pF |
 |
Zündkennlinien-Streubereiche bei R1 = 0,1 MΩ und Rg1 = 10 MΩ,
wie sie durch die Unterschiede bei der Röhrenherstellung,
durch Alterungserscheinungen der Röhren sowie durch Unter-
heizung oder Überheitzung auftreten können.
Berlin, den 21. Febr. 1964
Geheime Verschlußsache
MfS 006/137/64
Vorläufiges Pflichtenheft
für Programmiergerät T 150
Ein Programmiergerät ist so umzubauen, daß nachstehende
Forderungen erfüllt werden:
1. Aufgabenstellung
Das Programmiergerät ist mit insgesamt 32 Lesern auszustatten.
Alle Leser sind 5-Kanal-Leser. Die Lochkombinationen entsprechen
denen des Internationalen Telegraphenalphabets Nr. 2 (ITA)
1.1. Bezeichnung der Leser
Die Leser 1 - 26 werden fortlaufend mit den Buchstaben
A - Z bezeichnet. Für die restlichen 6 Leser sind folgende
Symbole zu verwenden:
Leser 27: ̸O
28: #
29: Ɔ
30: »
31: ∆
32: ↑
1.2. Auf-und Abwickelvorrichtung
Alle 32 Leser sollen eine Auf- und, Abwickelvorrichtung
besitzen. Der Leser 32 soll außerdem den Teleskop-
Streifenhalter beibehalten.
1.3.1. Der Leser 32 (Programmstreifenleser) steuert die rest-
lichen 31 Leser. Liest der Leser 32 die Kombination A,
so wird der Leser 1 (A) aufgerufen; liest er die Kom-
bination B, so wird der Leser 2 (B) aufgerufen usw.
Liest er die Kombination Zw, so wird der Leser 31 (∆)
aufgerufen.
Die Reihenfolge des Aufrufes der einzelnen Leser wird
durch einen Programmstreifen festgelegt. Dieser Programm-
streifen ist jeweils vor Inbetriebnahme des Gerätes her-
zustellen und in den Leser 32 einzulegen. Die von den
Lesern 1 - 31 gelesenen Kombinationen werden in einen
Streifen (Ausgangslochstreifen) gelocht.
1.3.2. Liest der Leser 32 die 32. Kombination (leer), so ist
diese Kombination in den Ausgangslochstreifen zu über-
nehmen.
1.3.3. Für den Leser 32 (Programmstreifenleser) muß Dauer-
und Einzelauslösung möglich sein.
1.4. Funktionen der Leser 1 - 31
1.4.1. Systematische Rückkehr zum Programmstreifen
Der Leser, der vom Leser 32 aufgerufen wird, gibt die
bei ihm anstehende Lochkombination des eingelegten
Lochstreifens an den Streifenlocher. Danach wird die
nächste Kombination im Leser 32 gelesen und der, der
Kombination entsprechende Leser aufgerufen.
Beispiel:
Programmstreifen
Kombinationsfolge: ACAZK
Lochstreifen im Leser 1 (A)
Kombinationsfolge: HUND
Lochstreifen im Leser 3(C)
Kombinationsfolge: ABCD
Lochstreifen im Leser 26(Z)
Kombinationsfolge: BODE
Lochstreifen im Leser 11 (K)
Kombinationsfolge: EFGH
Der Leser 32 liest die Kombination A und ruft damit
den Leser 1 auf. Der Leser 1 liest die Kombination H
und gibt sie an den Streifenlocher. Der Streifenlocher
stanzt die Kombination H. Danach liest der Leser 32 die
Kombination C und ruft den Leser 3 auf. Der Leser 3
liest die Kombination A und gibt sie an den Streifen-
locher. Der Streifenlocher stanzt die Kombination A.
Danach liest der Leser 32 die Kombination A und der
Zyklus wiederholt sich.
Jedem Lesevorgang im Leser 32 (Aufruf eines der Leser
1 - 31) entspricht also einem Lesevorgang in einem der
Leser 1 - 31 (systematische Rückkehr zum Programmstrei-
fen) und einem Stanzvorgang.
1.4.2.Bedingte Rückkehr zum Programmstreifen
Der Leser, der vom Leser 32 aufgerufen wird, gibt seine
Kombinationen solange an den Streifenlocher, bis er eine
32. Kombination liest. Diese 32. Kombination wird nicht
in den Ausgangslochstreifen übernommen. Sie gibt dem Leser
32 den Befehl, den nächsten Leser aufzurufen.
Beispiel:
Programmstreifen
Kombinationsfolge: ABA
Lochstreifen im Leser l (A)
Kombinationsfolge: ALLE∆↑ENTSCHEN∆↑
(∆: Zw; ↑ : 32. Kombination)
Lochstreifen im Leser 2 (B)
Kombinationsfolge: MEINE∆↑
Der Leser 32 liest die Kombination A und ruft damit den
Leser 1 auf. Dieser gibt seine Kombinationen ALLE∆ an
den Streifenlocher. Danach liest er die 32. Kombination.
Der Leser 32 erhält den Befehl weiterzulesen. Er liest
die Kombination B und ruft damit den Leser B auf.
Dieser gibt seine Kombinationen MEINE∆ an den Streifen-
locher. Danach liest er die 32. Kombination und gibt dem
Leser 32 den Befehl weiterzulesen. Der Zyklus wiederholt
sich von neuem.
Jedem Lesevorgang im Leser 32 entspricht also einer Reihe
von Lesevorgängen im aufgerufenen Leser und einer Reihe
von Stanzvorgängen (bedingte Rückkehr zum Programmstreifen).
1.4.3. Jeder der Leser 1 - 31 muß unabhängig voneinander
- abgeschaltet werden können, d.h. wenn er aufgerufen
wird, so gibt er keine Kombinationen an den Streifen-
locher. Der Leser 32 liest danach die nächste Kombi-
nation und ruft damit den nächsten Leser auf.
- auf die systematische Rückkehr zum Programmstreifen
eingestellt werden können;
- auf die bedingte Rückkehr zum Programmstreifen ein-
gestellt werden können.
1.5. Sonderfunktion des Lesers 1
1.5.1. Alle vom Leser 1 gelesenen Kombinationen sollen wahl-
weise unabhängig voneinander ausgeblendet oder in eine
beliebige der 32 möglichen Kombinationen des ITA umge-
schlüsselt werden können. Die Einstellungen für die
einzelnen Kombinationen sind vor Beginn der Arbeit
manuell vorzunehmen.
1.5.2. Zur Realisierung der unter Pkt. 1.5.1. genannten For-
derung ist der im Industriegerät bereits vorhandene
Umschlüssler so zu erweitern, daß er entsprechend dem
ITA für jede der 32 möglichen Kombinationen einen
Eingang besitzt.
1.5.3. Die 32 Ausgänge der Relaispyramide, die 32 Eingänge
des Umschlüsslers und der Eingang der Ausblendschal-
tung sind auf eine Programmtafel zu führen. Die Aus-
gänge der Relaispyramide sind als Einzelbuchsen, die
Eingänge des Umschlüsslers als Doppelbuchsen und der
Eingang der Ausblendschaltung als Multibuchse mit 10
Einzelbuchsen auszuführen.
Die Programmtafel soll außerdem ein Multibuchsenfeld
von mindestens 80 Multibuchsen mit je 5 Einzelbuchsen
besitzen.
Die Programmtafel soll auswechselbar sein. Insgesamt
werden 10 Programmtafeln benötigt.
Für die Herstellung der Programmtafeln sind Buchsen-
streifen, die in der Lochkartentechnik bzw. Büroma-
schinentechnik zur Herstellung von Programmtafeln
dienen, zu verwenden.
1.5.4. Der Leser 1 muß wahlweise auf Sonderfunktion oder auf
die normale Funktion, bei der die Leser 1 - 31 gleich-
berechtigt sind, eingestellt werden können.
1.5.5. Wird der Leser 1 auf Sonderfunktion eingestellt, so muß
es nach wie vor möglich sein, bei Ansteuerung der Leser
2 - 31 durch den Leser 32, die in den Lesern 2 - 31
anstehenden Kombinationen in den Ausgangslochstreifen
zu übernehmen.
2. Kontrolleinrichtung
Das Programmiergerät ist mit einer Kontrolleinrichtung zu
versehen, die die vom Leser 32 abgerufenen und zu kontrol-
lierenden Informationen der Leser 1 31 vor dem Ablochen
kontrolliert.
Sie besteht aus einer Folgenkontroll- und einer Folgenzähl-
einrichtung. Die Leser 1-31 müssen wahlweise und vonein-
ander unabhängig der Kontrolleinrichtung zugeschaltet werden
können.
2.1. Folgenkontrolleinrichtung
Die aus den Lesern 1 31 abgerufenen und zu kontrollieren-
den Informationen sind auf Folgen gleicher Kombinationen
bestimmter Länge zu überprüfen und auf Folgen gleicher
Kombinationen der maximal zugelassenen und vorwählbaren
Länge m (m = 1 … 8) zu reduzieren.
Das Einstellen der gewünschten Länge muß vor Beginn der
Arbeit manuell möglich sein.
Beispiel:
Es sei
m = 2;
Folge der zu kontrollierenden Informationen vor der
Kontrolleinrichtung:
ACCCCDEFFGGGH
Folge der zu kontrollierenden Informationen nach der
Kontrolleinrichtung:
ACCDEFFGGH
Die am Ausgang der Kontrolleinrichtung gegenüber dem
Eingang fehlenden Informationen werden ausgeblendet.
2.2. Folgenzähleinrichtung
Die Folgenzähleinrichtung muß die Folgen gleicher Kombi-
nationen der Längen 1 bis m (m = 1 … 8) der zu
kontrollierenden Informationen e i n z e l n zählen.
Diese Zählergebnisse weisen die Zähler 1 bis 8 aus.
Alle Folgen gleicher Kombinationen der Länge k (k > m)
sind mit dem Zähler 9 zu zählen.
Zur Anzeige sind neun, mindestens vierstellige ziffernan-
zeigende Zähler (Hengstler-Zähler) zu verwenden.
2.2.1. Arbeitsweise der Zähleinrichtung
Folgt einer beliebigen Kombination des ITA eine von
ihr abweichende Kombination, so erhält der Zähler 1
einen Zählimpuls. Folgt auf zwei gleichen Kombinationen
des ITA eine von ihnen abweichende Kombination, so
erhält der Zähler 2 einen Zählimpuls usw.
Ist die vorgewählte Länge m erreicht, so erhält der
Zähler m einen Zählimpuls. Bei Längen k (k > m) der
zu kontrollierenden Folgen gleicher Kombinationen erhält
der Zähler 9 bei der (m + 1)sten Kombination einen Zähl-
impuls. Die übrigen [k - (m + 1)] Kombinationen bewirken
keine Änderung der Zähleranzeige.
Beispiel:
Es sei
m = 3;
Folge der zu kontrollierenden Informationen vor der
Kontrolleinrichtung:
AABCDDDDEFGHHIIIIIIJKLLLM
Folge der zu kontrollierenden Informationen nach der
Kontrolleinrichtung:
AABCDDDEFGHHIIIJKLLLM
Folgende Zähleranzeige muß vorliegen:
Zähler 1: 8 (B,C,E,F,G,J,K,M)
Zähler 2: 2 (AA, HH)
Zähler 3: 3 (DDD, III, LLL)
Zähler 4: 0
Zähler 5: 0
Zähler 6: 0
Zähler 7: 0
Zähler 8: 0
Zähler 9: 2 (DDDD, IIIIII)
2.2.2. Konstruktive Gestaltung der Kontrolleinrichtung
Die Kontrolleinrichtung ist als konstruktive selbst-
ständige Baugruppe auszuführen.
Alle Ausgangs- und Eingangsleitungen sind an genormte
Steckerleisten zu führen.
3. Vergleichereinrichtung
Das Programmiergerät ist mit einer Vergleichereinrichtung
auszustatten, die wahlweise abschaltbar ist. Für den Ver-
gleich sind zweckmässigerweise die Leser 1 - 16 vorzusehen.
3.1. Nur Vergleichen
Es muß möglich sein, wahlweise 2 - 16 Lochstreifen gleich-
zeitig miteinander zu vergleichen. Bei dieser Betriebsart
ist der Ausgangsstreifenlocher abgeschaltet. Bei Ungleich-
heit wird der Vergleich der Streifen gestoppt. Eine op-
tische Anzeige muß angeben, welcher Leser in Bezug auf
Leser 1 die falsche Kombination abgetastet hat.
3.2. Vergleichen, Programmieren und Ablochen
Es muß möglich sein, wahlweise 2 - 16 Lochstreifen gleich-
zeitig miteinander zu vergleichen. Der Vergleich ist so
durchzuführen, daß bei Gleichheit die von den zu verglei-
chenden Lochstreifen gleichzeitig abgetastete Kombination
in den Ausgangslochstreifen gestanzt wird.
Bei Ungleichheit müssen folgende Möglichkeiten bestehen:
- Bei Ungleichheit mindestens einer der gleichzeitig ab-
getasteten Kombinationen muß in den Ausgangslochstreifen
die 32. Kombination gestanzt werden.
- Eine Programmierung des Ausgangslochstreifens muß mög-
lich sein, indem Informationen aus den Lesern 17 - 32
abgerufen werden können. Dabei ist eine systematische
Rückkehr zum Programmstreifen vorzusehen.
- Die gleichzeitig abgetasteten, aber nicht übereinstim-
menden Kombinationen werden überlesen und in den Aus-
gangslochstreifen wird nichts gelocht.
Es werden alle Leser und der Ausgangsstreifenlocher ge-
stoppt. Eine optische Anzeige muß angeben welcher Leser
in Bezug auf den Leser 1 die falsche Kombination abge-
tastet hat.
Referat 1 A / 1 T Berlin, den 15. 11. 1965
Auftrag des Vorganges T 153
Bearbeitung des Vorganges T 153
Zur Vereinfachung der Herstellung komplizierter programmierter
Lochstreifen sind in Verbindung mit OTS Programmiergeräte mit
5 Sendeköpfen auszurüsten. Die Programmiergeräte sind durch
Zusätze so zu erweitern, daß eine teilweise automatische Krypto-
logische Kontrolle der Streifen möglich ist.
Alle bei der Bearbeitung anfallenden Schriftstücke u. ä. sind
unter dem Aktenzeichen T 153 zu erfassen.
…
Pflichtenfestlegung für Programmiergerät T 153
Ein Programmiergerät ist so umzubauen, daß nachstehende For-
derungen erfüllt werden:
1. Aufgabenstellung
Das Programmiergerät ist mit insgesamt 6 Lesern auszustatten.
Alle Leser sind 5-Kanalleser. Die Lochkombinationen entsprechen
denen des Internationalen Telegraphenalphabets Nr. 2 (ITA)
1.1. Bezeichnung der Leser
Die ersten fünf Leser sind fortlaufend mit den Ziffern 1 - 5
und der 6. Leser mit dem Buchstaben P zu bezeichnen.
1.2. Auf- und Abwickelvorrichtung
Die Leser 1- 5 sollen eine Auf- und Abwickelvorrichtung be-
sitzen. An jedem Leser sollte ein Teleskopstreifenhalter be-
festigt werden können.
1.3. Funktion des Lesers P
1.3.1. Der Leser P (Programmstreifenleser) steuert die rest-
lichen 5 Leser. Liest er die Lochkombination E, so wird der
Leser 1 (Lochung im ersten Kanal) aufgerufen, bei der Loch-
kombination Zeilenvorschub (Lochung im 2. Kanal) der 2. Leser,
bei der Lochkombination Zwischenraum der 3. Leser, bei der
Lochkombination Wagenrücklauf der 4. Leser und bei der Loch-
kombination T der 5. Leser.
1.3.2. Liest der Leser P die 32. Kombination (leer), so ist
diese Kombination in den Ausgangslochstreifen zu übernehmen.
1.3.3. Werden vom Leser gleichzeitig mehr als ein Leser ange-
rufen, so hat das Programmiergerät anzuhalten.
1.3.4. Für den Leser P muß Dauer- und Einzelauslösung möglich sein.
1.4. Funktion der Leser 1 - 5
1.4.1. Systematische Rückkehr zum Programmstreifen
Der Leser, der vom Leser P aufgerufen wird, gibt die bei ihm
anstehende Lochkombination des eingelegten Lochstreifens an
den Streifenlocher, der diese in den Ausgangsstreifen locht.
Danach wird die nächste Kombination im Leser P gelesen und
der, der Kombination entsprechenden Leser aufgerufen usw.
Jedem Lesevorgang im Leser P entspricht also ein Lesevorgang
in dem aufgerufenen Leser und ein Stanzvorgang.
Beispiel:
Programmstreifen
Kombinationsfolge: E, ZW, E, WR, T
Lochstreifen im Leser 1
Kombinationsfolge: H, I, J, K
Lochstreifen im Leser 3
Kombinationsfolge: A, B, C, D
Lochstreifen im Leser 4
Kombinationsfolge: B, C, D, E
Lochstreifen im Leser 5
Kombinationsfolge: E, F, G, H
Der Leser P liest die Kombination E und ruft damit den Leser 1
auf. Der Leser 1 liest die Kombination H und gibt sie an den
Streifenlocher. Der Streifenlocher stanzt die Kombination H.
Danach liest der Leser P die Kombination ZW und ruft den Leser 3
auf. Der Leser 3 liest die anstehende Lochkombination A und
gibt sie an den Streifenlocher, von dem sie gestanzt wird.
Danach liest der Leser P die Kombination E. Er ruft den Leser 1
auf usw.
1.4.2. Bedingte Rückkehr zum Programmstreifen
Der Leser, der vom Leser P aufgerufen wird, gibt seine Kombi-
nation solange an den Streifenlocher, bis er eine 32. Kombi-
nation liest. Diese 32. Kombination wird nicht in den Ausgangs-
lochstreifen übernommen. Sie gibt dem Leser P den Befehl, den
nächsten Leser aufzurufen.
Jedem Lesevorgang im Leser P entspricht einer Reihe von Lesevor-
gängen im aufgerufenen Leser und der gleichen Anzahl Stanzvor-
gängen.
Beispiel:
Programmstreifen
Kombinationsfolge: E T E
Lochstreifen im Leser 1
Kombinationsfolge: ENTWURF∆↑FESTLEGUNG
(∆: Zw; ↑ : 32. Kombination)
Lochstreifen im Leser 5
Kombinationsfolge: PFLICHTEN↑
Der Leser P liest die Kombination E und ruft damit den Leser 1
auf. Dieser gibt die Folge von Kombinationen ENTWURF ∆ an den
Streifenlocher. Danach liest er die 32. Kombination. Damit er-
hält der Leser P den Befehl, den nächsten Leser aufzurufen.
Er liest dann die Kombination T und ruft damit den Leser 5 auf.
Dieser gibt die Folge von Kombinationen PFLICHTEN an den
Streifenlocher. Danach liest er die 32. Kombination und gibt
dem Leser P den Befehl, die nächstfolgenden Kombination zu
lesen usw.
1.4.3. Schaltmöglichkeiten
Jeder der Leser 1 - 5 muß unabhängig von den anderen
- abgeschaltet werden können, d. h. wenn er aufgerufen wird,
gibt er keine Kombinationen an den Streifenlocher. Der
Leser P liest dann automatisch die nächste Kombination und
ruft den entsprechenden Leser auf;
- auf die systematische Rückkehr zum Programmstreifen einge-
stellt werden können;
- auf die bedingte Rückkehr zum Programmstreifen eingestellt
werden können.
1.5. Sonderfunktionen des Leser 1
Der Leser 1 muß unabhängig von anderen Einstellungen auf
folgende Betriebsarten von Hand aus einstellbar sein
- Betriebsart 32 Kombinationen \
- Betriebsart 26 Buchstaben } programmiert
- Betriebsart 10 Ziffern /
2. Kontrolleinrichtung
Das Programmiergerät ist mit einer Kontrolleinrichtung zu ver-
sehen, die die vom Leser P abgerufenen Informationen der Leser
1 - 5 vor dem Ablochen kontrolliert. Die Kontrolleinrichtung
besteht aus einer Folgenkontroll- und einer Folgenzähleinrich-
tung. Es muß möglich sein, jeden der 5 Leser unabhängig vonein-
ander mit in die Kontrolle einzubeziehen oder von der Kontrolle
auszuschließen.
2.1. Folgenkontrolleinrichtung
Die von den Lesern abgerufenen und zu kontrollierenden Infor-
mationen sind auf Folgen gleicher Kombinationen bestimmter
Länge zu überprüfen. Vor Beginn der Arbeit muß es möglich
sein, eine maximal zulässige Länge m (1 ≤ m ≤ 8) der Folgen
gleicher Kombinationen manuelle einzustellen. Alle auftreten-
den Folgen von gleichen Kombinationen, die länger als diese
Zahl m sind, sind auf die Länge zu reduzieren. Die überzäh-
ligen Kombinationen sind auszublenden.
Beispiel:
Es sei m = 2; die Folge der zu kontrollierenden Informationen
vor der Kontrolleinrichtung lautete:
ACCCCDEAAGGGH
Dann lautet die Folge der kontrollierten Informationen nach
Durchgang durch die Kontrolleinrichtung:
ACCDEAAGGH.
2.2. Folgenzähleinrichtung
Die Folgenzähleinrichtung muß die Folgen gleicher Kombina-
tionen der Länge 1 bis m (1 ≤ m ≤ 8) der zu kontrollieren-
den Informationen einzeln zählen.
Diese Zählergebnisse weisen die Zähler 1 bis 8 aus.
Alle Folgen gleicher Kombinationen der Länge k (k > m) sind
mit dem Zähler 9 zu zählen.
Zur Anzeige sind 9 mindestens vierstellige ziffernanzeigende
Zähler (Hengstler-Zähler) zu verwenden.
2.2.1. Arbeitsweise der Zähleinrichtung
Folgt einer beliebigen Kombination des ITA eine von ihr ab-
weichende Kombination, so erhält der Zähler 1 einen Zähl-
impuls. Folgt auf zwei gleiche Kombinationen des ITA eine von
ihnen abweichende Kombination, so erhält der Zähler 2 einen
Zählimpuls usw.
Ist die vorgewählte Länge m erreicht, so erhält der Zähler m
einen Zählimpuls. Bei Längen k (k > m) der zu kontrollierenden
Folgen gleicher Kombination erhält der Zähler 9 bei der
(m + 1).ten Kombinationen erhält einen Zählimpuls. Die übrigen
k - m - 1 Kombinationen bewirken keine Änderung der Zähl-
anzeige.
Beispiel:
Es sei m = 3
Die Folge der zu kontrollierenden Informationen vor der Kon-
trolleinrichtung lautete:
AABCDDDDEFGHHBBBBBBJKLLLL
Es muß nach dem Durchlaufen der Folgenzähleinrichtung folgen-
de Zähleranzeige vorliegen
Zähler 1: 8 (B, C, E, F, G, J, K, M)
Zähler 2: 2 (AA, HH)
Zähler 3: 1 (LLL)
Zähler 9: 2 (DDDD, BBBBBB)
2.2.2. Konstruktive Gestaltung der Kontrolleinrichtung
Die Kontrolleinrichtung ist als selbständige konstruktive
Baugruppe auszuführen.
Alle Ausgangs- und Eingangsleitungen sind an genormte Stecker-
leisten zu führen.
(Es ist möglich, daß sich nach Abschluß mathematischer Unter-
suchung eine Präzisierung oder Abschwächung der Anforderungen
an die Folgenkontroll- und Folgenzähleinrichtung ergibt).
Arbeitsgebiet 111 Berlin, 25. September 1980 bis
Geheime Verschlußsache 24. März 1986
MfS 020 Nr.: XI/702/80
01. Ausf. 11 Blatt
Autoren: Schneider, Hauptmann
Kaiser, Hauptmann
Einverstanden: Krey, Major
Untersuchungsergebnisse zu MISCHUNG
Inhaltsverzeichnis
Literaturverzeichnis
Einleitung
1. Begründung der Untersuchungen zum Thema MISCHUNG
2. Inhalt des Themas MISCHUNG
3. Definition und Charakterisierung des Algorithmus
des paarweisen Vertauschens (APV)
4. Literaturübersicht zu APV
5. Zum Charakter des vorliegenden Dokuments
Nachtrag zur Einleitung
6. Die Realisierung des APV auf EDVA bei Verwendung eines
physikalischen Zufallsgenerators
Teil I: Erzeugung einer Permutation oder Anordnung durch APV
Teil II: Erzeugung von Folgen von Permutationen oder Anord-
nungen mittels des APV
Teil III: Anwendung des APV zur Chiffriermittelproduktion
Literaturverzeichnis
/1/ Beschluß zur Eröffnung des Themas MISCHUNG XI/098/78
/2/ Algorithmus zur Erzeugung von Zufallspermutationen und
Zufallsanordnungen (2. Exemplar mit Begründungen)
VVS XI/751/78
/3/ Guy de Balbine, Note on Random Permutations. Mathematics
of Computation, Vol. 21, No. 100 (1967)
/4/ Пиpьянoвич B.A., Oб oднoм эффekтибнoм мeтoдe пoлучeния
cлучaйныx пepecтaнoвok.
"Aвтoмaтизиpoвaнныe cиcтeмы плaнoвыx pacчeтoв в pecпублиkaнckиx
плaнoвыx opгaнax" выпуck 9 (I977)
/5/ Mathematik für Kryptologen XI/1/696/75
/6/ Fisz, Wahrscheinlichkeitsrechnung und mathematische Statistik; Berlin, 1958
/7/ A.Renyi, Wahrscheinlichkeitsrechnung; Berlin, 1962
/8/ Kнут, Иckуccтвo пpoгpaммиpoвaния для ЭВM.
T.2: Пoлучиcлeнныe aлгopитмы Mockвa I977
/9/ Sloane, Encrypting by Random Rotations.
Lecture Notes in Computer Science,
Vol. 149, pp. 71 - 128
(Proceedings of the Workshop an Cryptography,
Burg Feuerstein, Germany, March 29 - April 2, 1982)
/10/ Pиopдaн, Bвeдeниe в koмбинaтopный aнaлиз, Mockвa I963
/11/ Axo, Xoпkpoфт, Ульмaн, Пocтpoeниe и aнaлиз вычиcлитeльныx
aлгopитмoв. Mockвa I979
/12/ Vorschrift zur Herstellung von Permutationen/Anordnungen
mit der DV-Technik PRS 4000 mit Peripherie
VVS XI/766/83
Einleitung
1. Begründung der Untersuchungen zum Thema MISCHUNG
Anlaß für die Untersuchungen zum Thema MISCHUNG, deren Ergeb-
nisse in diesem Dokument festgehalten werden, war der Verschleiß
der EDVA GAMMA 10 und die dadurch notwendig gewordene Neueinfüh-
rung der EDVA PRS 4000. Damit verbunden war die Umstellung der
Produktion der bisher auf dem GAMMA 10 hergestellten Chiffrier-
mittel bzw. Manuskripte für Chiffriermittel auf die EDVA PRS 4000.
Durch die verbesserten Leistungsparameter des PRS 4000 bezüglich
Rechengeschwindigkeit und Speicherkapazität ergaben sich neue Mög-
lichkeiten für die Verbesserung der Qualität der Mittelproduktion
auf EDVA. Es sollte eine rationellere, effektivere und standardi-
sierte Herstellung und Überprüfung der Mittel erreicht werden. Das
Thema MISCHUNG sollte alle Arbeiten zur Erreichung dieser Zielstel-
lung für die Produktion von Mitteln auf der Grundlage von zufälli-
gen Permutationen umfassen, siehe EröffnungsbeschluB /1/.
Die zu erarbeitende Lösung sollte umfassend und langfristig stabil
sein und dabei gleichzeitig eine flexible Anpassung an die Bedarfs-
entwicklung, die Entwicklung der Peripherie des PRS 4000 und andere
veränderliche Bedingungen ermöglichen.
Nach Sichtung der Literatur und Überlegungen zum Vergleich verschie-
dener Erzeugungsvorschriften wurde unter Beachtung kryptologischer
Aspekte sowie der Möglichkeiten günstiger programm- und rechentech-
nischer Realisierungen in Hinblick auf eine rationelle und standar-
disierte Gesamttechnologie der Mittelproduktion entschieden, als
grundsätzliche Erzeugungsvorschrift für die Herstellung zufälliger
Permutationen und Anordnungen den Algorithmus des paarweisen Ver-
tauschens APV anzuwenden /2/.
Die in der offenen Literatur gefundenen Eigenschaften des APV waren
für die kryptologische Anwendung nicht ausreichend, auch gab es kei-
ne eigenen Untersuchungen zu diesem Algorithmus, da er bisher bei uns
nicht angewendet wurde.
Daraus ergab sich die Notwendigkeit eigener Untersuchungen im Rah-
men des Themas MISCHUNG.
2. Inhalt des Themas MISCHUNG
Seit dem Eröffnungsbeschluß zum Thema MISCHUNG /1/ hat sich der In-
halt des Themas etwas geändert.
Unter dem Thema MISCHUNG im Sinne des vorliegenden Dokuments ver-
stehen wir ein kryptologisches Untersuchungsthema, das die krypto-
logischen Aspekte der Produktion der Chiffriermittel, die mittels
APV erzeugte zufällige Permutationen und Anordnungen darstellen
bzw. auf diesen basieren, umfaßt. Somit gehören zum Thema MISCHUNG:
- mathematische Untersuchungen des APV
- kryptologische Untersuchungen von Realisierungen des APV zur
Chiffriermittelproduktion
- Untersuchungen kryptologischer Aspekte der Technologie der Chif-
friermittelproduktion bei Verwendung des APV, insbesondere Un-
tersuchungen zur Wirksamkeit der kryptologischen Kontrollen.
3. Definition und Charakterisierung des Algorithmus des
paarweisen Vertauschens APV
Der APV ist ein Algorithmus zur Umwandlung einer Permutation (Aus-
gangspermutation) n-ten Grades, n-1 ∈ N, in eine andere Permuta-
tion (Ergebnispermutation) n-ten Grades unter Benutzung von n-1
reellen Zahlen aus dem Intervall (0,1); d. h. einschließlich 0 und
ausschließlich 1.
Er ist weiterhin zur Erzeugung einer Anordnung von k aus n Elemen-
ten, k ∈ 1,n-1, aus einer Permutation n-ten Grades verwendbar. Un-
ter einer Anordnung verstehen wir eine geordnete Auswahl von k Ele-
menten aus einer n-elementigen Menge ohne Wiederholung (kurz: k-An-
ordnung).
Die Elemente der Ausgangs-und Ergebnispermutation sowie der Anord-
nung gehören ein und derselben Menge an.
Definition APV:
Gegeben seien die Ausgangspermutation
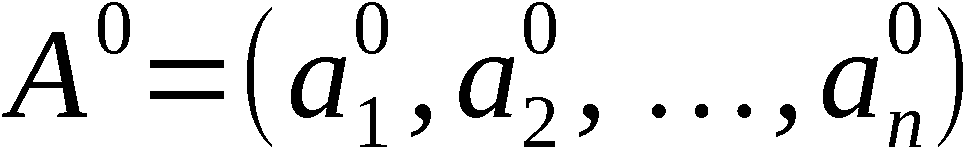
und die Zahlenfolge

Wir definieren ∀ i ∈ 1,n-1:

Mit diesen Bezeichnungen ist An-1 die Ergebnispermutation, symbo-
lisch:
An-1 = PVn (A0)
und A(k) mit k ∈ 1,n-1 die erzeugte k-Anordnung, symbolisch:
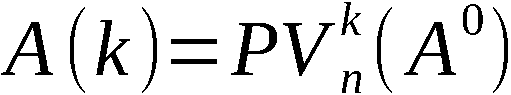
Zur Erzeugung von An-1 bzw. A(k) werden somit n-1 bzw. k Schritte
des Algorithmus abgearbeitet. Im i-ten Schritt, i ∈ 1,n-1 bzw. i ∈ 1,k,
wird aus der Permutation Ai-1 durch Vertauschung der Elemente an
den Stellen i und i + ηi ∈ i,n, wobei alle anderen Elemente unverändert
bleiben, die Permutation Ai erzeugt.
Für die Erzeugung von zufälligen Permutationen und Anordnungen für
kryptologische Anwendungen ist der Algorithmus APV aufgrund der
nachfolgend bewiesenen Eigenschaften interessant.
Satz 1:
Wenn die Folge  eine Folge unabhängiger Realisierungen einer auf
(0,1) gleichverteilten (stetigen) Zufallsgröße X ist, dann sind bei
beliebiger Ausgangspermutation (a1, a2, … , an) alle Ergebnisper-
mutationen gleichwahrscheinlich.
Beweis:
Sei
eine Folge unabhängiger Realisierungen einer auf
(0,1) gleichverteilten (stetigen) Zufallsgröße X ist, dann sind bei
beliebiger Ausgangspermutation (a1, a2, … , an) alle Ergebnisper-
mutationen gleichwahrscheinlich.
Beweis:
Sei  die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige Permutation
die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige Permutation 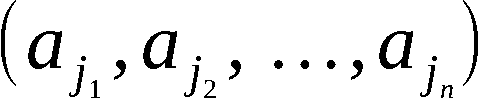 zu erhalten.
Es gilt
zu erhalten.
Es gilt
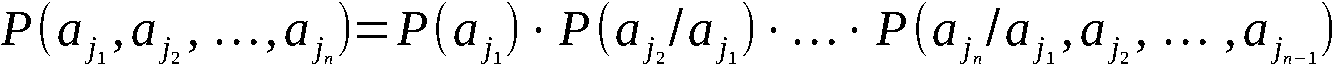
wobei  -Wahrscheinlichkeit dafür, daß an
r-ter Stelle das Element
-Wahrscheinlichkeit dafür, daß an
r-ter Stelle das Element 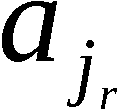 , erscheint unter der Bedingung, daß
, erscheint unter der Bedingung, daß
 an den Stellen 1, 2, … , r-1 stehen (r ∈ 2,n).
Infolge der Gleichverteilung von X auf (0,1) gilt
an den Stellen 1, 2, … , r-1 stehen (r ∈ 2,n).
Infolge der Gleichverteilung von X auf (0,1) gilt
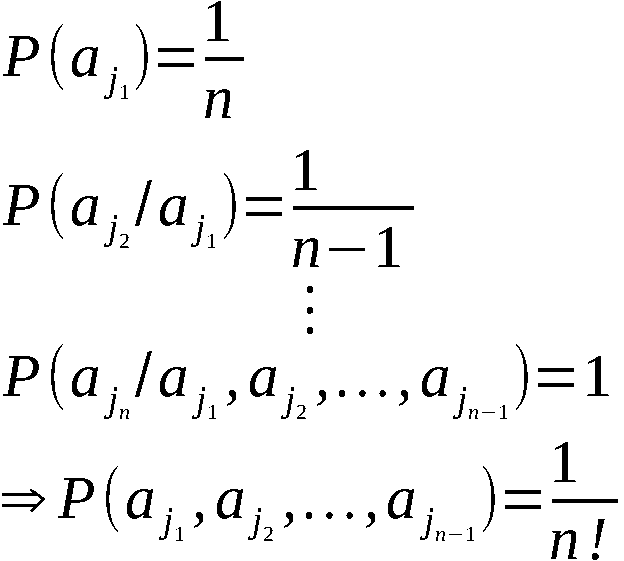
Da 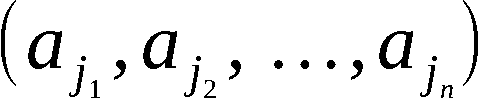 eine beliebige der n! möglichen Ergebnis-
permutationen ist, sind damit alle Ergebnispermutationen gleich-
wahrscheinlich.
Satz 2:
Wenn für fixiertes k ∈ 1,n-1 die Folge
eine beliebige der n! möglichen Ergebnis-
permutationen ist, sind damit alle Ergebnispermutationen gleich-
wahrscheinlich.
Satz 2:
Wenn für fixiertes k ∈ 1,n-1 die Folge  eine Folge unabhän-
giger Realisierungen einer auf (0,1) gleichverteilten Zufallsgröße
ist, dann sind bei beliebiger Ausgangspermutation alle k-Anordnun-
gen gleichwahrscheinlich.
Beweis:
Sei
eine Folge unabhän-
giger Realisierungen einer auf (0,1) gleichverteilten Zufallsgröße
ist, dann sind bei beliebiger Ausgangspermutation alle k-Anordnun-
gen gleichwahrscheinlich.
Beweis:
Sei 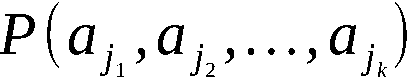 die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige k-Anordnung
die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige k-Anordnung  zu erhalten.
Es gilt
zu erhalten.
Es gilt

(Bezeichnungen analog Beweis zu Satz 1)
Infolge der Gleichverteilung von X gilt
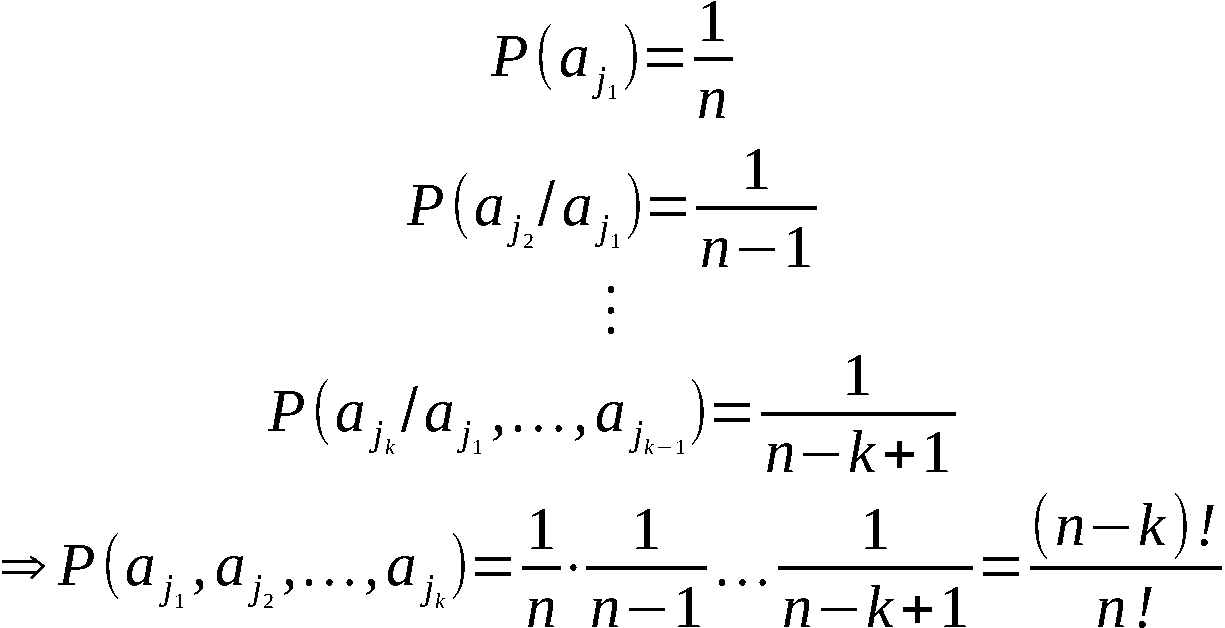
Da  eine beliebige der
eine beliebige der  möglichen k-An-
ordnungen ist, sind damit alle Anordnungen gleichwahrscheinlich.
Bei der Entscheidung, APV als grundsätzliche Erzeugungsvorschrift
für die Herstellung von zufälligen Permutationen und Anordnungen
anzuwenden, wurden u. a. folgende Charakteristika von APV berück-
sichtigt:
(1) APV erfaßt Permutationen und Anordnungen und ist für alle prak-
tisch notwendigen Grade n der Permutationen auf PRS 4000 zu
realisieren.
(2) Die Anzahl der notwendigen Schritte hängt nur von n bzw. k ab
und ist unabhängig von der Wahl von A0 und den konkreten Werten
ξi.
(3) Das Übergangsverhalten A0→An-1 bzw. A0→A(k) hängt nicht von
der Wahl von A0 ab (alle A0 sind gleichberechtigt).
4. Literaturübersicht zu APV
Der Algorithmus APV wurde in der in 3. beschriebenen Form in /3/ ver-
öffentlicht. Die kurze Notiz enthält neben der Beschreibung den Be-
weis, daß unter den Bedingungen des Satzes 1 die Wahrscheinlichkeit
dafür, daß ein vorgegebenes Element an der m-ten Stelle der Ergebnis-
permutation steht, 1/n beträgt (n-Grad der Permutation) und der Erwar-
tungswert für die Anzahl der Vertauschungen gleich
möglichen k-An-
ordnungen ist, sind damit alle Anordnungen gleichwahrscheinlich.
Bei der Entscheidung, APV als grundsätzliche Erzeugungsvorschrift
für die Herstellung von zufälligen Permutationen und Anordnungen
anzuwenden, wurden u. a. folgende Charakteristika von APV berück-
sichtigt:
(1) APV erfaßt Permutationen und Anordnungen und ist für alle prak-
tisch notwendigen Grade n der Permutationen auf PRS 4000 zu
realisieren.
(2) Die Anzahl der notwendigen Schritte hängt nur von n bzw. k ab
und ist unabhängig von der Wahl von A0 und den konkreten Werten
ξi.
(3) Das Übergangsverhalten A0→An-1 bzw. A0→A(k) hängt nicht von
der Wahl von A0 ab (alle A0 sind gleichberechtigt).
4. Literaturübersicht zu APV
Der Algorithmus APV wurde in der in 3. beschriebenen Form in /3/ ver-
öffentlicht. Die kurze Notiz enthält neben der Beschreibung den Be-
weis, daß unter den Bedingungen des Satzes 1 die Wahrscheinlichkeit
dafür, daß ein vorgegebenes Element an der m-ten Stelle der Ergebnis-
permutation steht, 1/n beträgt (n-Grad der Permutation) und der Erwar-
tungswert für die Anzahl der Vertauschungen gleich 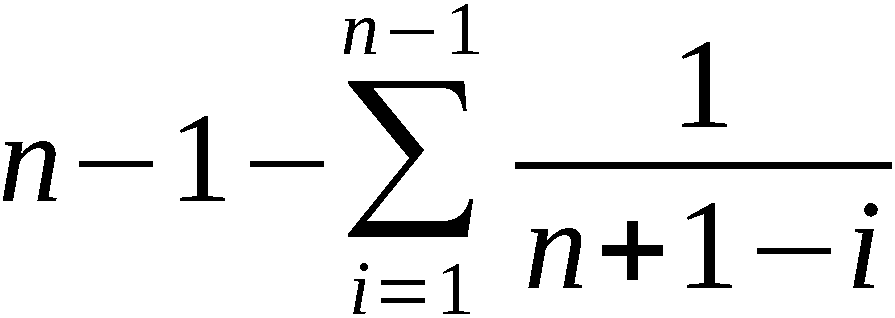 ist.
Es wird bemerkt, daß kleine Abweichungen von der Gleichverteilung in
den kleinsten signifikanten Digitalstellen der Realisierungen der auf
(0,1) gleich verteilten Zufallsgröße praktisch keinen Einfluß auf die
Verteilung der Zufallspermutationen haben.
In verallgemeinerter Form wurde der Algorithmus auch in einer sowje-
tischen Quelle beschrieben /4/. Die Verallgemeinerung besteht in der
Verwendung der Zahlenfolge
ist.
Es wird bemerkt, daß kleine Abweichungen von der Gleichverteilung in
den kleinsten signifikanten Digitalstellen der Realisierungen der auf
(0,1) gleich verteilten Zufallsgröße praktisch keinen Einfluß auf die
Verteilung der Zufallspermutationen haben.
In verallgemeinerter Form wurde der Algorithmus auch in einer sowje-
tischen Quelle beschrieben /4/. Die Verallgemeinerung besteht in der
Verwendung der Zahlenfolge

Es wird definiert:
ηi = : ent (ξi · i + 1), i = n, n-1, …, 2
und die Vertauschung beginnt beim letzten Element  der Ausgangspermutation, d. h.
der Ausgangspermutation, d. h.
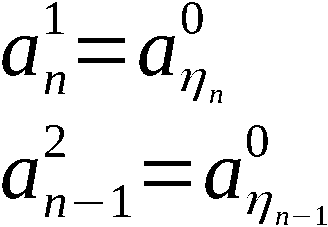
usw.
Satz 1 gilt hier unter den Voraussetzungen, daß α = 1 und ξi-Reali-
sierung einer auf (0,1) gleichverteilten Zufallsgröße ist.
Für verschiedene α werden verschiedene, für α ≠ 1 von der Gleich-
verteilung abweichende Verteilungen der ηi erzielt.
Folgende Eigenschaft dieser Verallgemeinerung wurde gezeigt:

Weitere Hinweise auf Eigenschaften von APV und dessen Realisierung
auf EDVA wurden in der Literatur nicht gefunden.
Nachtrag: Eine Beschreibung des APV enthalten auch /8/, S. 155
(Algorithmus P), sowie /9/, wobei die Vertauschung beginnend mit
dem letzten Element der Permutation durchgeführt wird.
Sloane charakterisiert in /9/ APV als "sehr einfachen und schnellen
Algorithmus der über allen anderen steht".
5. Zum Charakter des vorliegenden Dokumentes
Das vorliegende Dokument erfaßt alle gesicherten Untersuchungser-
gebnisse zum Thema MISCHUNG.
Zum gegenwärtigen Zeitpunkt sind nicht alle aus kryptologischer
Sicht interessanten mathematischen Probleme gelöst. Auch konnten
die Untersuchungen zu kryptologischen Aspekten der Technologie der
Chiffriermittelproduktion nicht abgeschlossen werden, da diese Tech-
nologie gegenwärtig noch nicht vollständig festgelegt ist.
Deshalb werden diese Probleme schrittweise bearbeitet.
Um die effektive Erarbeitung dieses Dokumentes zu gewährleisten, ist
das Dokument erweiterbar gestaltet und die Ergebnisse der weiteren
Untersuchungen werden nach ihrem Abschluß in das Dokument eingear-
beitet.
Die ersten Teile des Dokumentes enthalten die theoretischen Grundla-
gen zum APV, soweit diese gesichert vorliegen. Spätere neue Erkennt-
nisse können nachgetragen werden.
Weitere Teile des Dokumentes sind kryptologische Analysen von Reali-
sierungen des APV sowie bestimmter Aspekte des technologischen Pro-
zesses der Chiffriermittelproduktion, die bis zu zusammenfassenden
Einschätzungen der kryptologischen Güte dieser Realisierungen bzw.
technologischen Prozesse gehen.
Damit ist dieses Dokument nicht Begründung für die Wahl konkreter
Realisierungen oder die Ablehnung anderer möglicher Varianten, son-
dern analysiert die ganz konkret realisierte Produktionstechnologie.
Das schließt jedoch nicht aus, daß andere mögliche Erzeugungsvor-
schriften, Realisierungen, Kontrollen u. ä. zur Einschätzung des Vor-
handenen als Vergleich herangezogen werden.
Das Dokument soll, genau wie die Produktionstechnologie, eine lang-
fristige Arbeitsgrundlage für die Produktion eines wesentlichen Teils
der Chiffriermittel darstellen.
Die im Dokument verwendeten Bezeichnungen, Schreibweisen u. ä.
entsprechen /5/, sofern sie nicht ausdrücklich anders definiert
sind.
Die in der APV-Definition verwendeten Bezeichnungen sind für das
gesamte Dokument verbindlich und dürfen nicht anderweitig benutzt
werden.
Nachtrag zur Einleitung
6. Die Realisierung des APV auf EDVA bei Verwendung eines
physikalischen Zufallsgenerators
In der praktischen Realisierung des Algorithmus APV auf EDVA
werden die in den Sätzen 1 und 2 der Einleitung verwendeten Vor-
aussetzungen zum Nachweis der Gleichwahrscheinlichkeit der Ergeb-
nispermutationen bzw. k-Anordnungen nicht erfüllt. So kann auf
EDVA nicht mit stetigen, sondern nur mit diskreten Zufallsgrößen
(DZG) gearbeitet werden. Für die Untersuchungen zu MISCHUNG werden
deshalb für das gesamte Dokument verbindlich folgende Voraus-
setzungen und die entsprechenden Bezeichnungen formuliert:
1. In der Definition APV (Punkt 3. der Einleitung)
ist die Zahlenfolge
 zu ersetzen durch die Zahlenfolge
zu ersetzen durch die Zahlenfolge  ∀ i ∈ 1,n-1: δi ∈ N(2ν), ν ∈ N beliebig fest.
Wir definieren ∀ i ∈ 1,n-1
∀ i ∈ 1,n-1: δi ∈ N(2ν), ν ∈ N beliebig fest.
Wir definieren ∀ i ∈ 1,n-1

Die Zahl ν wird als Grad der Approximation einer stetigen
Zufallsgröße durch DZG bezeichnet.
2. Für die Bildung der Zahlenfolge  gilt
gilt

 stellen unabhängige Realisierungen einer DZG dar, die den
Wert 1 mit der Wahrscheinlichkeit p und den Wert 0 mit der
Wahrscheinlichkeit q = 1-p annimmt.
Die Annahme der Unabhängigkeit der Realisierungen wird als zu-
lässig angesehen, weil für die Chiffriermittelproduktion von der
Verwendung eines physikalischen Zufallsgenerators ausgegangen
werden kann, der den notwendigen kryptologischen Kontrollen unter-
liegt und somit die Bedingung der Unabhängigkeit aufeinanderfol-
gender binärer Elemente hinreichend gut erfüllt.
Andererseits würde ohne diese Annahme der mathematische Unter-
suchungsaufwand stark anwachsen, teilweise müßten andere, kom-
pliziertere mathematische Mittel eingesetzt werden.
Aus dem gleichen Grund wird der in der Praxis auftretende Fall
eines zeitlich schwankenden p nicht speziell untersucht.
Die Monotonieeigenschaften aller untersuchten Eigenschaften,
die von p abhängen, lassen vermuten, daß für diese Eigenschaften
im Fall eines zeitlich schwankenden p eine Abschätzung, die auf
der kryptologisch sicheren Seite liegt, angegeben werden kann,
wenn für p der Wert konstant fest gehalten wird, der am stärksten
von ½ abweicht.
Aus den Eigenschaften von Zufallsgeneratoren für die Chiffrier-
mittelproduktion folgt außerdem, daß bei Notwendigkeit auch die
vereinfachende Annahme getroffen werden kann, daß p nur gering-
fügig von ½ abweicht.
7. Juli 1982
Teil I
Erzeugung einer Permutation oder Anordnung durch APV
Inhalt:
1. Aufgabenstellung und mathematisches Modell
2. Der Spezialfall p = ½
3. Der allgemeine Fall
3.1. Mathematische Grundlagen
3.2. Theoretische Aussagen
3.3. Numerische Aussagen
3.4. Ergänzung zu Punkt 3.2. und 3.3.
4. Bistochastische Matrizen
1. Aufgabenstellung und mathematisches Modell
Im vorliegenden Teil I werden die Eigenschaften des APV bei
einmaliger Anwendung auf eine Ausgangspermutation untersucht.
Mathematische interessieren dabei
- das zufällige Ereignis {An-1 = PVn(A0)}, das darin besteht,
daß bei Anwendung des APV auf eine gegebene Permutation A0 die
Permutation An-1 entsteht und
- das zufällige Ereignis
stellen unabhängige Realisierungen einer DZG dar, die den
Wert 1 mit der Wahrscheinlichkeit p und den Wert 0 mit der
Wahrscheinlichkeit q = 1-p annimmt.
Die Annahme der Unabhängigkeit der Realisierungen wird als zu-
lässig angesehen, weil für die Chiffriermittelproduktion von der
Verwendung eines physikalischen Zufallsgenerators ausgegangen
werden kann, der den notwendigen kryptologischen Kontrollen unter-
liegt und somit die Bedingung der Unabhängigkeit aufeinanderfol-
gender binärer Elemente hinreichend gut erfüllt.
Andererseits würde ohne diese Annahme der mathematische Unter-
suchungsaufwand stark anwachsen, teilweise müßten andere, kom-
pliziertere mathematische Mittel eingesetzt werden.
Aus dem gleichen Grund wird der in der Praxis auftretende Fall
eines zeitlich schwankenden p nicht speziell untersucht.
Die Monotonieeigenschaften aller untersuchten Eigenschaften,
die von p abhängen, lassen vermuten, daß für diese Eigenschaften
im Fall eines zeitlich schwankenden p eine Abschätzung, die auf
der kryptologisch sicheren Seite liegt, angegeben werden kann,
wenn für p der Wert konstant fest gehalten wird, der am stärksten
von ½ abweicht.
Aus den Eigenschaften von Zufallsgeneratoren für die Chiffrier-
mittelproduktion folgt außerdem, daß bei Notwendigkeit auch die
vereinfachende Annahme getroffen werden kann, daß p nur gering-
fügig von ½ abweicht.
7. Juli 1982
Teil I
Erzeugung einer Permutation oder Anordnung durch APV
Inhalt:
1. Aufgabenstellung und mathematisches Modell
2. Der Spezialfall p = ½
3. Der allgemeine Fall
3.1. Mathematische Grundlagen
3.2. Theoretische Aussagen
3.3. Numerische Aussagen
3.4. Ergänzung zu Punkt 3.2. und 3.3.
4. Bistochastische Matrizen
1. Aufgabenstellung und mathematisches Modell
Im vorliegenden Teil I werden die Eigenschaften des APV bei
einmaliger Anwendung auf eine Ausgangspermutation untersucht.
Mathematische interessieren dabei
- das zufällige Ereignis {An-1 = PVn(A0)}, das darin besteht,
daß bei Anwendung des APV auf eine gegebene Permutation A0 die
Permutation An-1 entsteht und
- das zufällige Ereignis 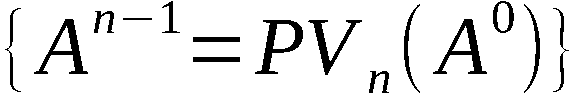 , das darin besteht,
daß bei Anwendung des APV auf A0 die Anordnung A(k) entsteht.
Bei der Anwendung des APV wird in jedem Schritt ein zufälliges Ereignis
Ei,j realisiert, das darin besteht, daß die DZG ηi den Wert j
annimmt, wobei i ∈ 1,n-1 und j ∈ 0, n-i.
Für ein fest vorgegebenes A0 kann jedem der n! möglichen Ereignisse
{An-1 = PV(A0)} eineindeutig ein Produkt von Ergebnissen Ei,j
zugeordnet werden:
, das darin besteht,
daß bei Anwendung des APV auf A0 die Anordnung A(k) entsteht.
Bei der Anwendung des APV wird in jedem Schritt ein zufälliges Ereignis
Ei,j realisiert, das darin besteht, daß die DZG ηi den Wert j
annimmt, wobei i ∈ 1,n-1 und j ∈ 0, n-i.
Für ein fest vorgegebenes A0 kann jedem der n! möglichen Ereignisse
{An-1 = PV(A0)} eineindeutig ein Produkt von Ergebnissen Ei,j
zugeordnet werden:
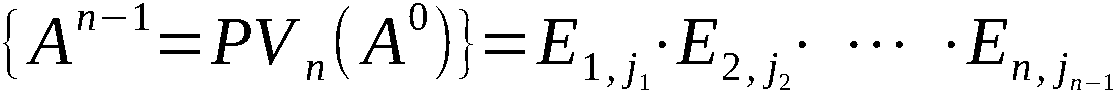
Es gibt offensichtlich genau n! solcher Produkte.
Seien folgende Wahrscheinlichkeiten definiert:
∀ i ∈ 1,n-1 ∀ j ∈ 0,n-i : πi,j = P(Ei,j) = P(ηi = j) (1.1)
Aus der vorausgesetzten Unabhängigkeit der Realisierung der DZG
folgt:
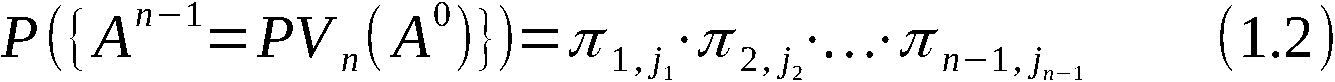
Beispiel: P({An-1 =A0}) = π1,0·π2,0·…·πn-1,0
Völlig analog erhalten wir für Anordnungen

Beispiel: Seien A0 = (1,2,…,n) und A(k) = (1,2,…,k-1),
dann ist  Zur weiteren Untersuchung der Wahrscheinlichkeiten πi,j zerlegen wir für
i ∈ 1,n-1 die Menge N(2ν) vollständig in disjunkte Untermengen
Zur weiteren Untersuchung der Wahrscheinlichkeiten πi,j zerlegen wir für
i ∈ 1,n-1 die Menge N(2ν) vollständig in disjunkte Untermengen  j ∈ 0,n-1:
j ∈ 0,n-1:

Offensichtlich wird das Ereignis Ei,j genau dann realisiert, wenn  Dann erhalten wir aus (1.1)
Dann erhalten wir aus (1.1)
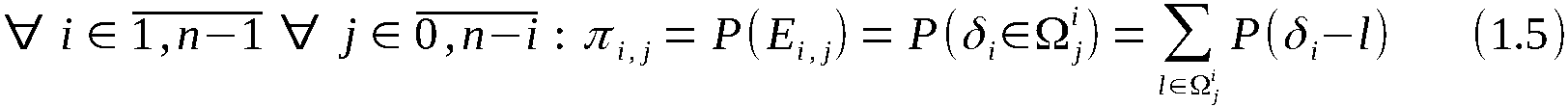
Für die weiteren Betrachtungen interessieren Aussagen über  .
Dazu benutzen wir, daß
.
Dazu benutzen wir, daß

Aus der Definition von 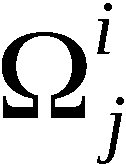 (1.4) folgt dann
(1.4) folgt dann

Diese Ungleichung genügen qi oder qi+1 Zahlen l∈N(2ν).
Da gilt
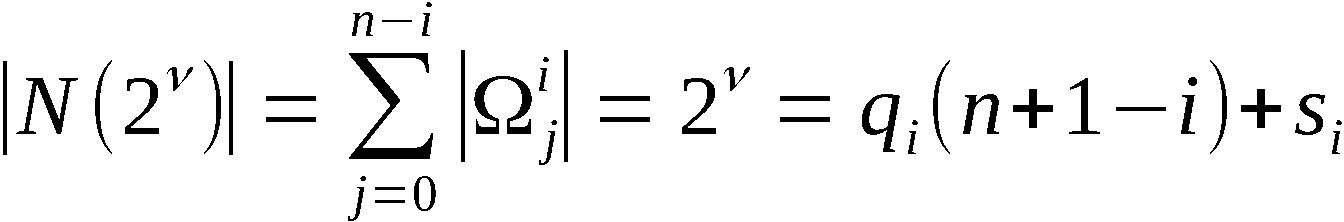
folgt daraus (1.6)
∀ i ∈ 1,n-1 gibt es genau si verschiedene j mit 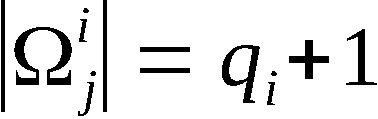 und n + 1 - si verschiedene j mit
und n + 1 - si verschiedene j mit  Durch die zusätzliche Forderung
2ν ≥ n (1.7)
wird gewährleistet, daß qi > 0 ist (∀ i ∈ 1,n-1).
Damit wird für die weiteren Betrachtungen der Fall πi,j ≡ 0
ausgeschlossen. Das bedeutet praktisch, daß keines der n! möglichen
Ereignisse {An-1=PVn(A0)} mit Wahrscheinlichkeit P ≡ 0 auftritt.
2. Der Spezialfall p = ½
Der Fall p = ½ entspricht der Verwendung einer
Durch die zusätzliche Forderung
2ν ≥ n (1.7)
wird gewährleistet, daß qi > 0 ist (∀ i ∈ 1,n-1).
Damit wird für die weiteren Betrachtungen der Fall πi,j ≡ 0
ausgeschlossen. Das bedeutet praktisch, daß keines der n! möglichen
Ereignisse {An-1=PVn(A0)} mit Wahrscheinlichkeit P ≡ 0 auftritt.
2. Der Spezialfall p = ½
Der Fall p = ½ entspricht der Verwendung einer idealen
Zufallsfolge zur
Bildung der Zahlenfolge  .
Jedoch wird auch bei Verwendung einer
.
Jedoch wird auch bei Verwendung einer idealen
Zufallsfolge keine
Gleichverteilung der erzeugten Permutationen erreicht. Die Ursache
dafür liegen in der möglichen Ungleichmächtigkeit der Mengen 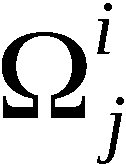 für verschiedene j bei festem i, vgl. (1.6).
Aus mathematischer Sicht ist der Fall p = ½ wesentlich einfacher und
überschaubarer als der allgemeine Fall.
Insbesondere gilt offensichtlich
für verschiedene j bei festem i, vgl. (1.6).
Aus mathematischer Sicht ist der Fall p = ½ wesentlich einfacher und
überschaubarer als der allgemeine Fall.
Insbesondere gilt offensichtlich
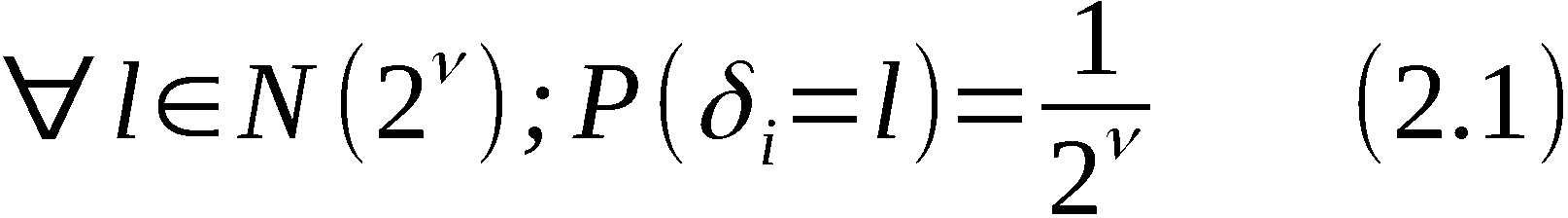
Dann folgt aus (1.5)
 Wir bezeichnen
(2.2)
Wir bezeichnen
(2.2)

Die Wahrscheinlichkeiten πi,j können dann nur die Werte π'i und π"i
annehmen
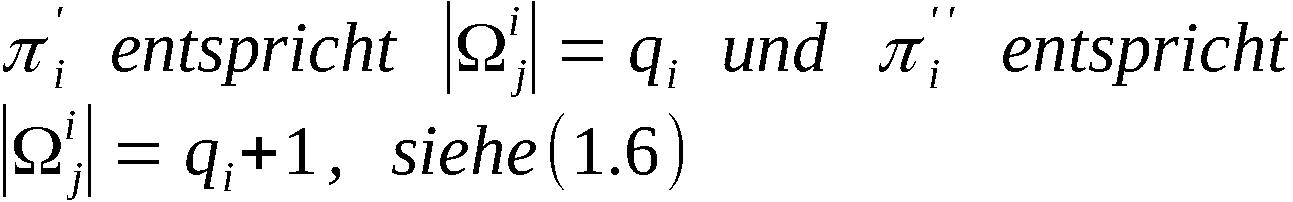
Bezeichnen wir weiterhin

so erhalten wir offensichtlich
P' ≤ P({An-1 = PVn(A0)}) ≤ P". (2.3)
Für n ≥ 3 und ν ≥ 2 gilt sogar
P' ≤ P({An-1 = PVn(A0)}) < P",
denn die Mengen  sind immer und die Mengen
sind immer und die Mengen 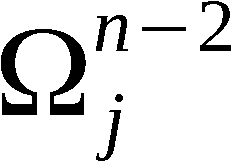 sind
nie gleichmächtig (für verschiedene j), somit kann in diesem Falle
keine Permutation An-1 mit der Wahrscheinlichkeit P"
auftreten.
Die Größe
sind
nie gleichmächtig (für verschiedene j), somit kann in diesem Falle
keine Permutation An-1 mit der Wahrscheinlichkeit P"
auftreten.
Die Größe
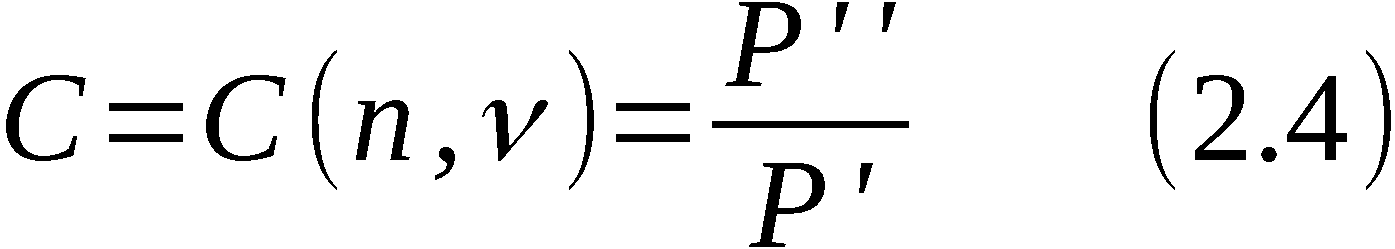
charakterisiert das Verhältnis der größten Wahrscheinlichkeit
zur kleinsten bei der Anwendung von APV zur Erzeugung einer
zufälligen Permutation als Funktion des Grades n der Permutation
und des Grades ν der Approximation der stetigen Zufalls-
größe durch eine diskrete.
Die Definition von C ist korrekt durch die Forderung 2ν ≥ n (vgl. (1.7))
wird garantiert, daß P' ≠ 0.
Für den Fall der Erzeugung von Anordnungen kann man die Größe

mit analoger Bedeutung definieren.
Dabei ist

und offensichtlich gilt

Weiter ist folgende Beziehung offensichtlich
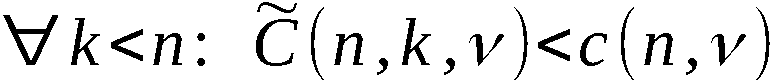
Von Interesse ist ebenfalls die maximale Abweichung der Wahr-
scheinlichkeit für das Entstehen einer Permutation bzw. An-
ordnung von der Wahrscheinlichkeit im Falle der Gleichvertei-
lung. Wir bezeichnen diese maximale Abweichung mit D(n,ν)
bzw. ͠D(n,ν,k). (obere Grenze für max. Abweichung!)
Es ist offensichtlich


Betrachten wir nun genauer die Größe C = C(n,ν).
Aus (2.4) und (2.2) folgt

Daraus ergibt sich folgende Abschätzung für C(n,ν)

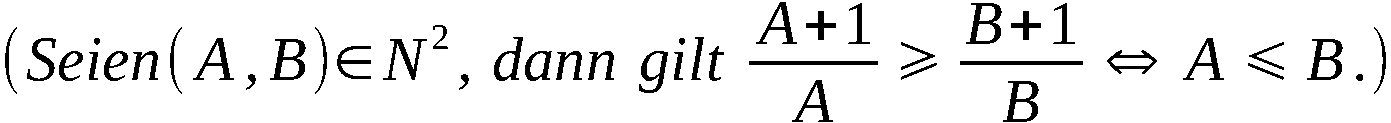
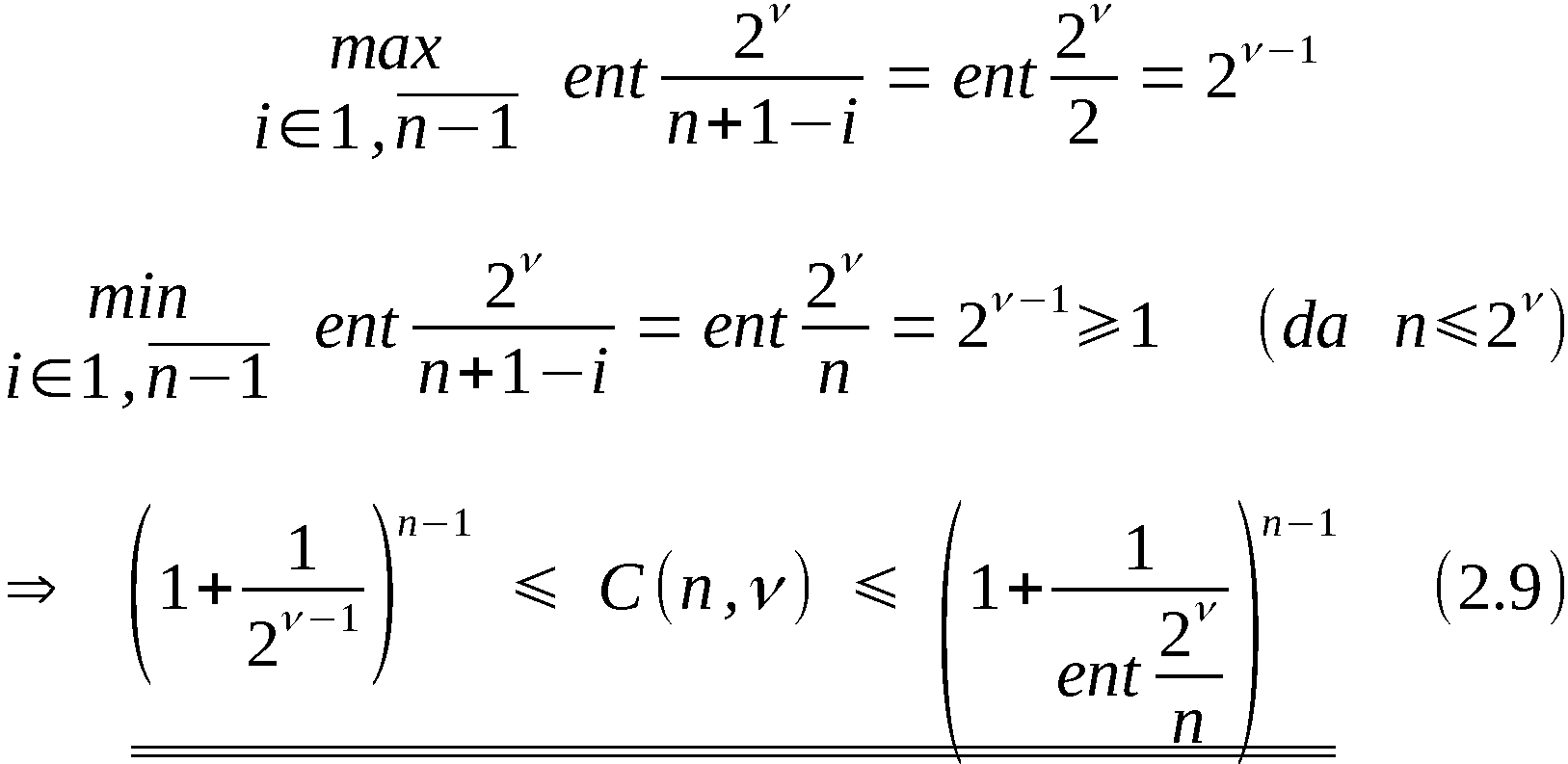
Schlußfolgerungen aus (2.9):
1. Für fixiertes ν wächst C(n,ν) mit wachsenden n (exponentiell).
2. Für fixiertes n wird mit wachsendem ν C(n,ν) kleiner.
Um die Größe C(n,ν) zu verdeutlichen, sind in der folgenden Tabelle 2.1
die nach der Formel (2.8) berechneten Werte von C(n,ν) für ausgewählte n
und praktisch interessierende ν angegeben
(ν = 15 und ν = 31 sind deshalb von praktischen Interesse, weil
sich für die Realisierung von APV auf einer EDVA die Darstellung der Zahlen
δi als Wort (15 bit + Vorzeichen)
bzw. Doppelwort (31 Bit + Vorzeichen) anbietet.)
| Tabelle 2.1: Werte für C(n,ν) |
|---|
| n | C(n,15) | C(n,31) |
| 10 | 1,0016 | 1,000 000 025 |
| 26 | 1,0107 | 1,000 000 163 |
| 32 | 1,016 | |
| 45 | 1,032 | |
| 100 | 1,167 | 1,000 002 351 |
| 200 | 1,846 | |
| 500 | 45,684 | 1,000 058 |
| 1 000 | 4.297.401,175 | 1,000 233 |
| 10 000 | - (n > 2ν) | ≤ 1,047 (*) |
| 100 000 | | ≤ 105,282 (*) |
| (*) Die Abschätzungen werden mit Formel (2.9) ermittelt. |
Da offensichtlich 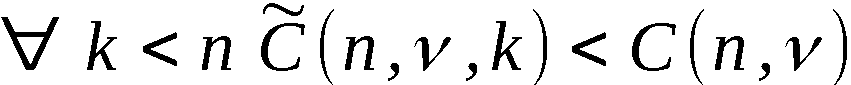 gilt, können
wir auf die Angabe genauer Wert für ͠C(n, ν,k) verzichten.
Die folgende Tabelle 2.2 enthält einige konkrete Werte D(n,ν)
die das Verhalten von D(n,ν) in Abhängigkeit von n und ν verdeut-
lichen soll. Die Berechnungen basieren auf (2.6) und (2.2).
Die Tabelle 2.2 zeigt:
1. Für fixiertes ν wird mit wachsendem n D(n,ν) relativ
zu 1/n! größer.
2. Für fixiertes n wird die Abweichung von 1/n! mit wachsendem ν
geringer.
gilt, können
wir auf die Angabe genauer Wert für ͠C(n, ν,k) verzichten.
Die folgende Tabelle 2.2 enthält einige konkrete Werte D(n,ν)
die das Verhalten von D(n,ν) in Abhängigkeit von n und ν verdeut-
lichen soll. Die Berechnungen basieren auf (2.6) und (2.2).
Die Tabelle 2.2 zeigt:
1. Für fixiertes ν wird mit wachsendem n D(n,ν) relativ
zu 1/n! größer.
2. Für fixiertes n wird die Abweichung von 1/n! mit wachsendem ν
geringer.
| Tabelle 2.2: Werte für D(n,ν) |
|---|
| n | D(n,15) | D(n,31) |
| 10 | 2,524 10-10 | = | 1/10! ·9,159 10-4 | 4,481 10-15 | = | 1/10! ·1,626 10-8 |
| 26 | 1,358 10-29 | = | 1/26! ·5,477 10-3 | 2,457 10-34 | = | 1/26! ·9,910 10-8 |
| 32 | 3,436 10-38 | = | 1/32! ·9,041 10-3 | 6,101 10-43 | = | 1/32! ·1,605 10-7 |
| 45 | 1,591 10-58 | = | 1/45! ·1,903 10-2 | 2,362 10-63 | = | 1/45! ·2,825 10-7 |
| 50 | 7,579 10-67 | = | 1/50! ·2,305 10-2 | 1,065 10-72 | = | 1/50! ·3,239 10-7 |
| 66 | 7,501 10-95 | = | 1/66! ·4,083 10-2 | 1,072 10-99 | = | 1/66! ·4,837 10-7 |
Betrachten wir abschließend noch einige ausgewählte konkrete Werte
für ͠D(n, ν,k):
| k | ͠D (10,15,k) | ͠D (10,31,k) |
| 7 | 8,24 10-4·3!/10! | 1,49 10-8·3!/10! |
| 5 | 6,41 10-4·5!/10! | 1,21 10-8·5!/10! |
| 2 | 4,88 10-4·8!/10! | 4,66 10-9·8!/10! |
| | | |
| k | ͠D (26,15,k) | |
| 20 | 5,08 10-3·6!/26! |
| 10 | 3,36 10-3·16!/26! |
| 5 | 1,83 10-3·21!/26! |
| 2 | 7,93 10-4·24!/26! |
| | |
| k | ͠D(32,31,k) |
| 26 | 1,55 10-7·6!/32! |
| 20 | 1,38 10-7·12!/32! |
| 10 | 7,87 10-8·22!/32! |
| 5 | 5,40 10-8·27!/32! |
Diese wenigen konkrete Werte für ͠D (n,ν,k) lassen die Schlußfolgerung
zu, daß für fixierte n und ν die Abweichung von 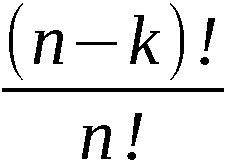 mit
fallendem k geringer wird (relativ zu
mit
fallendem k geringer wird (relativ zu 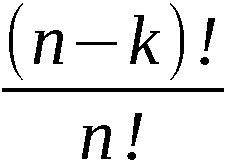 ).
3. Der allgemeine Fall
Für praktisch realisierte Zufallsgeneratoren trifft die Voraussetzung
p = ½ nicht zu.
Um für den allgemeinen Fall Aussagen über Eigenschaften des APV
bei einmaliger Anwendung zu erhalten, sind umfangreichere
Mathematische Grundlagen notwendig, die im Punkt 3.1. zusam-
mengefaßt sind.
3.1. Mathematische Grundlagen
Gegeben sei:
- n ∈ N beliebig fest
- eine diskrete Zufallsgröße Θ auf {0,1}, die den Wert 1
mit der Wahrscheinlichkeit p und den Wert 0 mit der Wahr-
scheinlichkeit q = 1-p annimmt.
Wir betrachten Elemente l ∈ N(2n) in der Darstellung
).
3. Der allgemeine Fall
Für praktisch realisierte Zufallsgeneratoren trifft die Voraussetzung
p = ½ nicht zu.
Um für den allgemeinen Fall Aussagen über Eigenschaften des APV
bei einmaliger Anwendung zu erhalten, sind umfangreichere
Mathematische Grundlagen notwendig, die im Punkt 3.1. zusam-
mengefaßt sind.
3.1. Mathematische Grundlagen
Gegeben sei:
- n ∈ N beliebig fest
- eine diskrete Zufallsgröße Θ auf {0,1}, die den Wert 1
mit der Wahrscheinlichkeit p und den Wert 0 mit der Wahr-
scheinlichkeit q = 1-p annimmt.
Wir betrachten Elemente l ∈ N(2n) in der Darstellung
Definition 1:
‖ Als Gewicht ‖l‖ des Elementes l wird die Summe der
‖ Koeffizienten der Dualdarstellung bezeichnet:
‖ ∀ l ∈ N(2n):  Weiterhin betrachten wir die diskrete Zufallsgröße δ auf N(2n)
mit
Weiterhin betrachten wir die diskrete Zufallsgröße δ auf N(2n)
mit
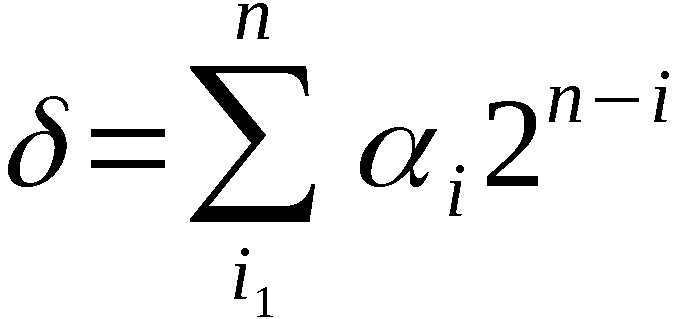
, wobei αi - unabhängige Realisierung der DZG Θ.
Satz 1:
‖ ∀ l ∈ N(2n) : P(δ = l) = p‖l‖ · q‖l‖.
Der Beweis ist offensichtlich aufgrund der in der Definition δ
vorausgesetzten Unabhängigkeit der Realisierung von Θ.
Definition 2:
‖ Seien  ‖ Eine eineindeutige Abbildung λ : I → I1 heißt
‖ kontrahierend, wenn
‖ λ z ∈ I : ‖λ‖ ≤ ‖z‖.
Aufgrund von Satz 1 sind folgende Eigenschaften der kontrahierenden
Abbildung λ offensichtlich:
(3.1)
1) p ≥ ½ → ∀ z ∈ I : P(δ = Θz) ≤ (δ = z)
2) p ≤ ½ → ∀ z ∈ I : P(δ = Θz) ≥ (δ = z)
3) p ≥ ½ → P(δ ∈ ΘI) ≤ (δ ∈ I)
4) p ≤ ½ → P(δ ∈ ΘI) ≥ (δ ∈ I)
Satz 2:
‖ ∀ k ≤ n : P(δ < 2k) = qn-k
Beweis: (mittels vollständiger Induktion)
k = 0 P(δ < 1) = P(δ=0) = qn (entspr. Satz 1)
k = 1 P(δ < 2) = P(δ = 0) + P(δ = 1) =
= qn + p · qn-1 = qn-1
k = m Sei P(δ < 2m) = qn-m
k = m+1 P(δ < 2m+1) + P(2m≤ δ < 2m+1)
Betrachten I = 2m, 2m+1 - 1 und I1 = N(2m)
Sei
‖ Eine eineindeutige Abbildung λ : I → I1 heißt
‖ kontrahierend, wenn
‖ λ z ∈ I : ‖λ‖ ≤ ‖z‖.
Aufgrund von Satz 1 sind folgende Eigenschaften der kontrahierenden
Abbildung λ offensichtlich:
(3.1)
1) p ≥ ½ → ∀ z ∈ I : P(δ = Θz) ≤ (δ = z)
2) p ≤ ½ → ∀ z ∈ I : P(δ = Θz) ≥ (δ = z)
3) p ≥ ½ → P(δ ∈ ΘI) ≤ (δ ∈ I)
4) p ≤ ½ → P(δ ∈ ΘI) ≥ (δ ∈ I)
Satz 2:
‖ ∀ k ≤ n : P(δ < 2k) = qn-k
Beweis: (mittels vollständiger Induktion)
k = 0 P(δ < 1) = P(δ=0) = qn (entspr. Satz 1)
k = 1 P(δ < 2) = P(δ = 0) + P(δ = 1) =
= qn + p · qn-1 = qn-1
k = m Sei P(δ < 2m) = qn-m
k = m+1 P(δ < 2m+1) + P(2m≤ δ < 2m+1)
Betrachten I = 2m, 2m+1 - 1 und I1 = N(2m)
Sei  Konstruktion einer eed Abbildung Θ von I auf I1:
Konstruktion einer eed Abbildung Θ von I auf I1:

Nach Definition 2 ist λ eine kontrahierende Abbildung,
aus der Konstruktion von λ folgt unmittelbar
‖z‖ = ‖z'‖ + 1.
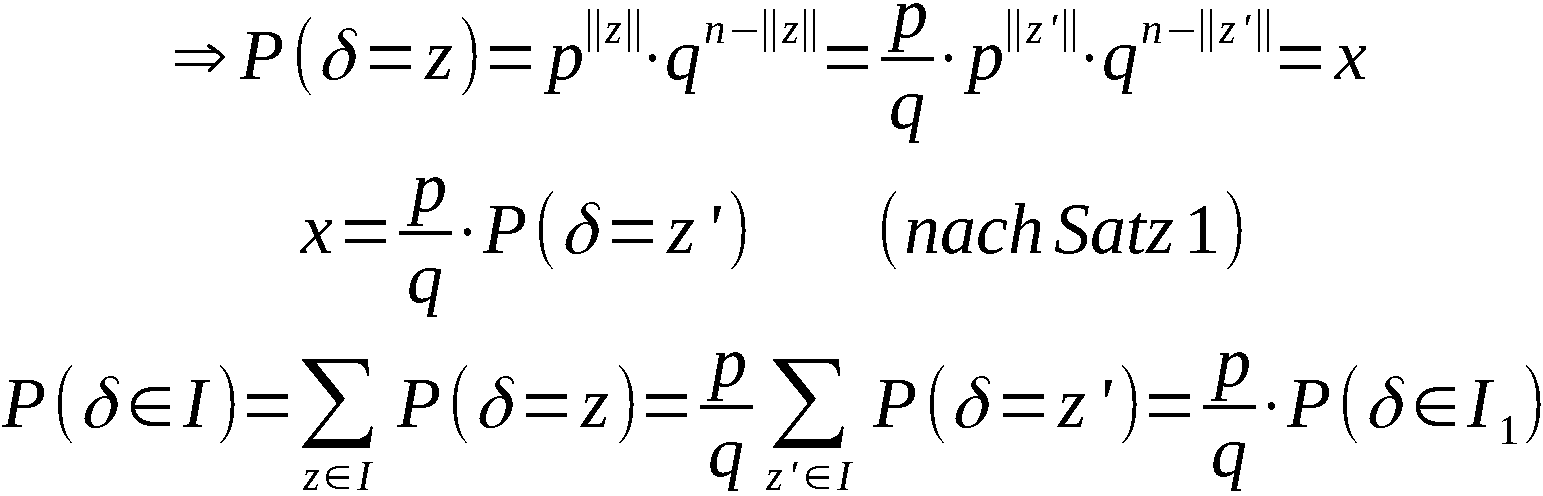
Nach Induktionsvoraussetzung gilt
P(δ ∈ I1) = P(δ < 2m) = qn-m
→ P(δ < 2m+1) = qn-m+p/q ·qn-m = qn-(m+1).
Nach der Methode der vollständigen Induktion ist damit
Satz 2 bewiesen (∀ k ≤ n).
Satz 3:

Beweis:
Sei  Wir ordnen alle die j Zahlen ai : ai = 1:
(3.2)
Wir ordnen alle die j Zahlen ai : ai = 1:
(3.2)

Sei

Offensichtlich gilt

Berechnung von P(δ ∈ Ik):
Wir betrachten Ik und I'k = N(2n-ik) und konstruieren
eine eed Abbildung λ von Ik auf I'k.
Seien

λ ist eine kontrahierende Abbildung, aus der Konstruktion von λ folgt
‖z'‖ = ‖z‖ - (k-1).
Aus Satz 1 folgt
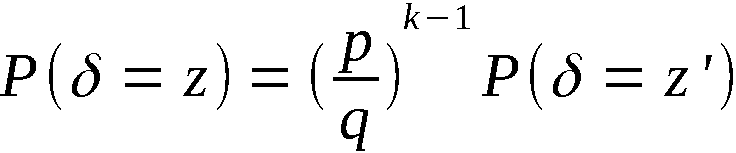
und allgemeiner
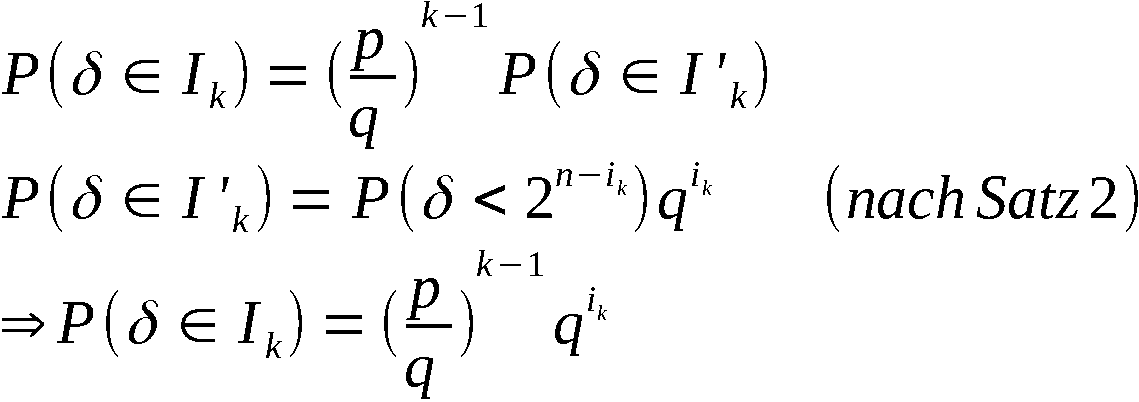
Eingesetzt in (3.3) erhalten wir

Aus (3.2) folgt

Um den Ausdruck P(δ < l) in der Formulierung von Satz 3
zu erhalten, ergänzen wir in der Summe noch die Summanden
für die i, für die ai = 0 gilt:

Definition 3:
‖ Die Abbildung δ : N(2n) → N(2n) wird definiert
‖ durch die Beziehung
‖ ∀ x ∈ N(2n) : δx = 2n-1-x
Die so definierte Abbildung δ realisiert die Zweierkomplement-
darstellung einer in Dualform dargestellten Zahl x in N(2n).
Folgende Eigenschaften der Abbildung δ ergeben sich unmittelbar
aus der Definition:
(3.4)
1) δ2 - identische Abbildung, d. h. ∀ x ∈ N(2n): δ2x = x
2) ‖δx‖ = n - ‖x‖
Satz 4:
‖ ∀(l,m) ∈ 1,2n-12 : m+l ≤ 2n
‖ sei λ eine kontrahierende Abbildung der Menge I2 = m,m+l-1
‖ auf die Menge I1 = 0,l-1 = N(l).
‖ Dann existiert ∀ (l', m') ∈ 1,2n-12 : m'+l' ≤ 2n
‖ eine kontrahierende Abbildung λ' der Menge I4 = 2n-l', 2n-1
‖ auf die Menge I3 = m',m'+l'- 1.
Beweis:
Auf die Mengen I4 und I3 werden wir die Abbildung δ (nach Def. 3) an:
δ(I4) = I'4 = 0, l'-1
δ(I3) = I'3 = 2n-m'-l', 2n-m'-1
Bezeichnen 2n-m'-l' = ͠m → I'3 = ͠m, ͠m+l'-1
Nach Voraussetzung existieren eine kontrahierende
Abbildung λ: I'3→I'4,
d. h. ∀z'3 ∈ I'3 Ǝ z'4=λz'3 ∈ I'4 : ‖z'4‖ ≤ ‖z'3‖.
Da λ-eed Abbildung, existiert die Umkehrabbildung λ-1:I'4→I'3,
d. h. ∀z'4 ∈ I'4 Ǝ Z'3 = λ-1z'4 ∈ I'3 : ‖z'3‖ ≥ ‖z'4‖.
Durch nochmalige Anwendung von δ erhalten wir
∀ z4 ∈ I4 : δλ-1δλz4 = δλ-1z'4 = δz'3 = δδz3 = z3 ∈ I3.
Betrachten die Gewichte:
‖z3‖ = ‖δλ-1z'4‖ = n - ‖λ-1z'4‖ (vgl. (3.4))
‖λ-1z'4‖ = ‖z'3‖ ≥ ‖z'4‖
→ ‖z3‖ ≤ n - ‖z'4‖ = n - ‖δz4‖ = ‖z4‖
→ Die Abbildung λ' = δλ-1δ ist eine kontrahierende
Abbildung der Menge I4 auf die Menge I3.
Satz 5:
‖ Sei I = m,m+l-1, m ∈ N(2n), l ∈ N : m + l ≤ 2n
‖ Dann existiert eine kontrahierende Abbildung der Menge I
‖ in die Menge N(2k),  , λ' ; I → N(2k),
‖ die eine der beiden Bedingungen erfüllt:
, λ' ; I → N(2k),
‖ die eine der beiden Bedingungen erfüllt:
 Beweis:
Seien
Beweis:
Seien
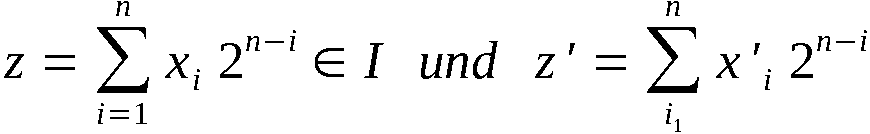
Wir definieren folgende Abbildung λ'

Für die so definierte Abbildung λ' ist offensichtlich λ' < 2k,
d. h. λ' z ∈ N(2k) eine eed Abbildung.
Aus der Konstruktion von λ' folgt

→ ∀ z ∈ I : ‖z‖ ≥ ‖λ'z‖.
→ λ' ist eine kontrahierende Abbildung von I in N(2k).
Betrachten I' = λ'I
Zur Veranschaulichung der Abbildung λ' wollen wir eine Skizze
betrachten. Dabei wird die Menge N(2n) als Menge von Punkten
auf dem Zahlenstrahl dargestellt. Dann besteht die Menge I
aus l < 2k Punkten und für die Lage von I sind
2 Fälle zu unterscheiden:
(1) Ǝ t ∈ N0 : t · 2k ≤ m < (t+1)2k, m+l <(t+1)2k

I' = s1,s2-1; s1 = m-t · 2k; s2 = s1+l
(2) Ǝ t ∈ N0: t · 2k ≤ m < (t+1)2k, m + l > (t+1) · 2k
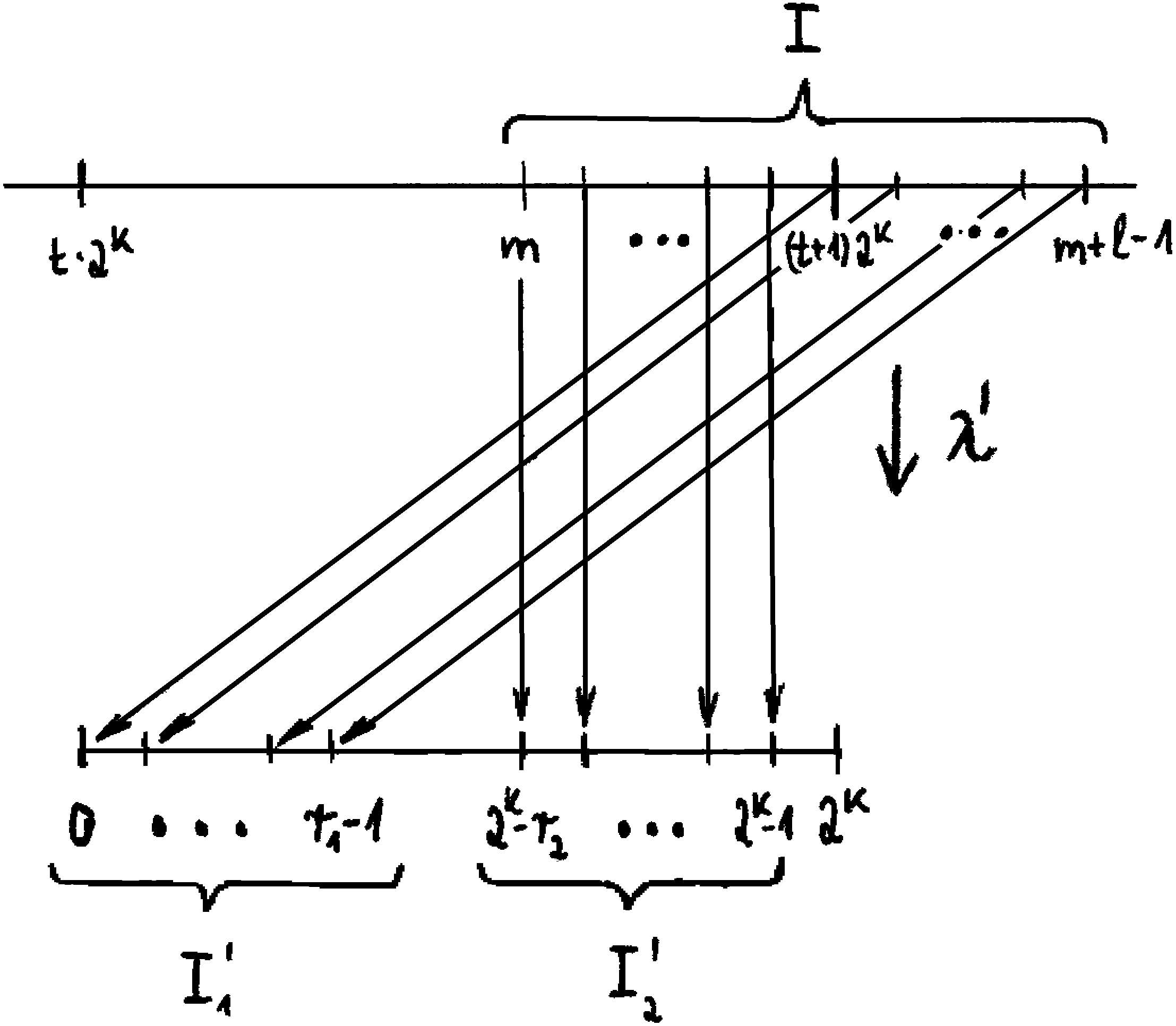
I' = 0,r4-1 U 2k-r2,2k-1;
r1 = m + l · 1 - (t+1) · 2k
r2 = (t+1) · 2k - m
r1 + r2 = l
Damit wurde gezeigt, daß I' = λI' eine der beiden Bedingungen
(1) oder (2) erfüllt.
Der folgende Satz 6 vertieft die Aussage von Satz 5 und gibt an, daß
eine kontrahierende Abbildung λ* so konstruiert werden kann, daß sie
die Menge I auf die Menge I0 = 0,l-1 abbildet.
Satz 6:
‖ Sie I = m,m+l-1, m ∈ N(2n), l ∈ N : m+l≤ 2n
‖ Dann existiert eine kontrahierende Abbildung λ* der Menge I
‖ auf die Menge I0 = 0,l-1 = N(l).
Beweis:
Wir beweisen diesen Satz mittels vollständiger Induktion.
Die Induktion wird dazu nach  durchgeführt.
Induktionsanfang:
k = 1 - trivialer Fall l = 1
I = {m} I0 = {0}
λ* : λ* m = 0
Offensichtlich gilt ∀ m ∈ N(2n)) : ‖m‖ ≥ ‖λ* m‖ = 0
→ λ* - kontrahierende Abbildung
k = 2 - 2 ≤ l < 4
· l = 2 I ={m,m+1} I0 = {0,1}
Nach Satz 5 existiert eine kontrahierende Abbildung λ´
von I in N(4), dabei sind folgende Mengen I' = λ´ I möglich:
durchgeführt.
Induktionsanfang:
k = 1 - trivialer Fall l = 1
I = {m} I0 = {0}
λ* : λ* m = 0
Offensichtlich gilt ∀ m ∈ N(2n)) : ‖m‖ ≥ ‖λ* m‖ = 0
→ λ* - kontrahierende Abbildung
k = 2 - 2 ≤ l < 4
· l = 2 I ={m,m+1} I0 = {0,1}
Nach Satz 5 existiert eine kontrahierende Abbildung λ´
von I in N(4), dabei sind folgende Mengen I' = λ´ I möglich:
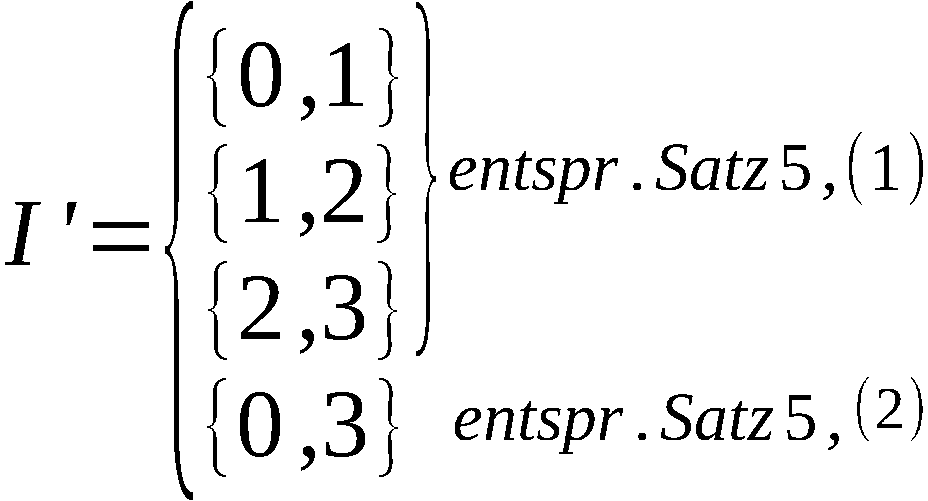
Konstruktion von λ" : I' → I0 :
Abbildung des i-ten Elements von I' auf das i-te Element von I0
Wie man leicht sieht, gilt ∀ z' ∈ I' : ‖z'‖ ≥ ‖λ" z'‖
→ Die Abbildung λ* = λ" ·' λ´ ist eine kontrahierende
Abbildung von I auf I0
(∀ z ∈ I : ‖λ* z‖ = ‖λ" z'‖ ≤ ‖z'‖ = ‖λ'z‖ ≤ ‖z‖)
· l = 3 I = {m, m+1, m+2} I0 = {0, 1, 2}
λ' - kontrahierende Abbildung von I in N(4) (nach Satz 5)
mögliche I' = λ'I :
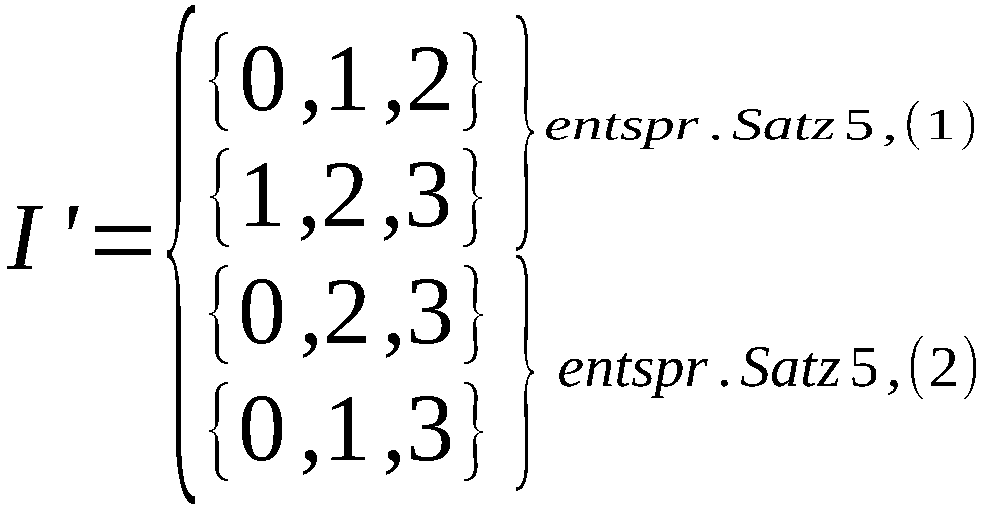
λ" : I' → I0 - Abbildung des i-ten Elements von I' auf i-tes Element von I0
λ" - kontrahierende Abbildung
→ λ* = λ" · λ' - kontrahierende Abbildung I → I0
Induktionsvoraussetzung:
k ≤ r Sei für beliebige k ≤ r die Existenz eine kontrahierende
Abbildung λ*k von I = m,m+l-1 mit 2k-1 ≤ l < 2k
auf I0 = 0,l-1 nachgewiesen.
Induktionsschritt:
k =r + 1 Nach Satz 5 existiert eine kontrahierende Abbildung λ'
von I in N(2r+1).
Wir betrachten I' = λ'I, dabei haben wir nach
Satz 5 zwei Fälle zu unterscheiden
(1) 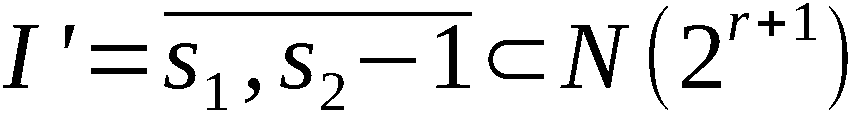 Konstruktion einer kontrahierenden Abbildung λ" von I' auf I0
Sei z ∈ I0, z' ∈ I'
∀ z' ∈ I0 ∩ I' : z = z', d. h. λ" = id
I0 ∩ I' = s1,l-1
Betrachten die Restmengen I*0 = 0,S1-1
und I* = l,s2-1
Diese Restmengen I*0 und I* haben die gleiche Mächtigkeit s1
Aus den Beziehungen 2r ≤ l < 2r+1 (k = r + 1!)
und s2 < 2r+1
folgt s1 < 2r, da s1 = s2 - l ist.
Damit existiert nach Induktionsvoraussetzung eine kontrahierende
Abbildung λ*r von I* auf I*0
Konstruktion einer kontrahierenden Abbildung λ" von I' auf I0
Sei z ∈ I0, z' ∈ I'
∀ z' ∈ I0 ∩ I' : z = z', d. h. λ" = id
I0 ∩ I' = s1,l-1
Betrachten die Restmengen I*0 = 0,S1-1
und I* = l,s2-1
Diese Restmengen I*0 und I* haben die gleiche Mächtigkeit s1
Aus den Beziehungen 2r ≤ l < 2r+1 (k = r + 1!)
und s2 < 2r+1
folgt s1 < 2r, da s1 = s2 - l ist.
Damit existiert nach Induktionsvoraussetzung eine kontrahierende
Abbildung λ*r von I* auf I*0

→ Die Abbildung λ* = λ" · λ' ist eine kontrahierende
Abbildung von I auf I0.
(2)  Konstruktion einer kontrahierenden Abbildung λ" von I' auf I0:
Wie im Fall (1) wird λ" so gewählt, daß
∀ z' ∈ I0 ∩ I' : z = z', d. h. λ" = id
Betrachten auch hier die Restmengen
Konstruktion einer kontrahierenden Abbildung λ" von I' auf I0:
Wie im Fall (1) wird λ" so gewählt, daß
∀ z' ∈ I0 ∩ I' : z = z', d. h. λ" = id
Betrachten auch hier die Restmengen
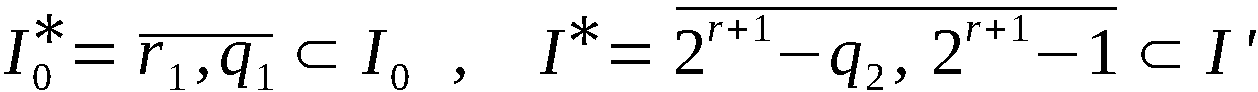
( Die konkreten Werte q1 und q2 hängen von r2 und l ab:
· l ≤ 2r+1 - r2 → I*0 = r1,l-1, I* = 2r+1-r2,2r+1-1
· l > 2r+1 - r2 → I*0 = r1,2r+1,r2-1, I* = l,2r+1-1 )
Die Mengen I*0 und I* haben die gleiche Mächtigkeit q2,
man kann leicht überprüfen, daß q2 < 2r.
Nach Induktionsvoraussetzung existiert ∀ ͠l < 2r eine
kontrahierende Abbildung der Menge ͠m,͠m+͠l-1 auf die
Menge 0,͠l-1.
Nach Satz 4 existiert dann eine kontrahierende Abbildung ͠λ
der Menge 2r+1-͠l,2r+1-1 auf die Menge ͠m,͠m+͠l-1,
d. h. ͠λ ist eine kontrahierende Abbildung von I* auf I*0.
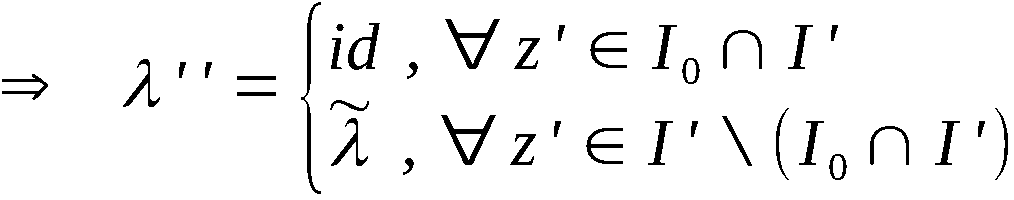
→ λ* = λ" · λ' ist eine kontrahierende Abbildung
von I auf I0
Nach der Methode der vollständigen Induktion ist damit Satz 6 bewiesen.
Als Abschluß der in diesem Punkte zusammengefaßten mathematischen
Grundlagen beweisen wir noch folgende für die weiteren Untersuchungen
wesentlichen Satz:
Satz 7:
‖ Sie m ∈ N(2n), l ∈ N : m + l ≤ 2n
‖ Dann gilt:
‖ 1. ∀ p < ½ : P(δ < l) ≥ P(m ≤ δ < m + l) ≥ P(2n - l ≤ δ < 2n))
‖ 2. ∀ p > ½ : P(δ < l) ≤ P(m ≤ δ < m + l) ≤ P(2n - l ≤ δ < 2n))
Anmerkung:
Für p = ½ gilt offensichtlich P(δ < l) = P(m ≤ δ < m + l) = P(2n - l ≤ δ < 2n).
Beweis:
Nach Satz 6 existiert eine kontrahierende Abbildung δ der Menge
I = m,m+l-1 auf die Menge I0 = 0,l-1.
Aus den Eigenschaften der kontrahierenden Abbildung δ folgt unmittel-
bar (vergl. (3.1)):
∀ p < ½ : P(δ ∈ I0) ≥ P(δ ∈ I)
∀ p > ½ : P(δ ∈ I0) ≤ P(δ ∈ I)
Nach Satz 4 folgt aus der Existenz von δ : I → I0
die Existenz einer kontrahierenden Abbildung λ' von der Menge
I1 = 2n-l,2n-1 auf I.
Dann gilt aufgrund der Eigenschaften der kontrahierenden Abbildung
∀ p < ½ : P(δ ∈ I0) ≥ P(δ ∈ I1)
∀ p > ½ : P(δ ∈ I0) ≤ P(δ ∈ I1)
3.2. Theoretische Aussagen
Im allgemeinen Fall gilt die Voraussetzung p = ½ nicht.
Damit kann auch die für die Untersuchung im Pkt. 2 grundlegende
Aussage (2.1)
∀ l ∈ N(2ν) : P(δi = l) = 1/2iν
für die Untersuchung im allgemeinen Fall nicht angewendet werden.
Nach Satz 1 gilt im allgemeinen Fall
P(δi = l) = p‖l‖ · qν-‖l‖

Aus (1.5) wird deutlich, daß im allgemeinen Fall die Wahrscheinlichkeit
πi,j von p abhängt.
Im weiteren verdeutlichen wir bei Notwendigkeit die Abhängigkeit von p
durch die Schreibweise
πi,j(p) und P(·/p).
Aus Satz 3 folgt

und aus Satz 7 folgt ∀(m,l) ∈ N(2ν)xN : m + l ≤2ν
1. ∀p < ½ : P(δi < l) ≥ P(m ≤ δi < m + l) ≥ P(2ν - l ≤ δi < 2ν)
2. ∀p > ½ : P(δi < l) ≤ P(m ≤ δi < m + l) ≥ P(2ν - l ≥ δi < 2ν)
(3.7)
Betrachten wir zunächst den Fall p > ½.
Da 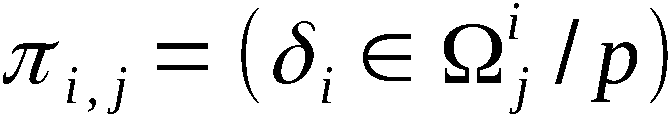 und die Mächtigkeit von
und die Mächtigkeit von 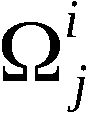 entweder
entweder 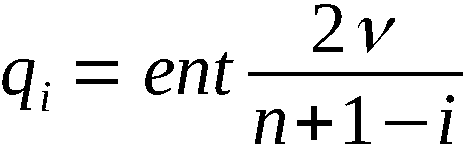 oder qi + 1 beträgt (vergl. (1.6)),
folgt aus (3.7)
∀ p > ½ : P(δi < qi/p) ≤ πi,j(p) ≤ P(2ν - qi ≤ δi < 2ν/p) (3.8)
P(δi < qi) ist die kleinste Wahrscheinlichkeit für die Mengen
oder qi + 1 beträgt (vergl. (1.6)),
folgt aus (3.7)
∀ p > ½ : P(δi < qi/p) ≤ πi,j(p) ≤ P(2ν - qi ≤ δi < 2ν/p) (3.8)
P(δi < qi) ist die kleinste Wahrscheinlichkeit für die Mengen 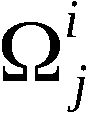 der Mächtigkeit qi,
P(2ν - qi - 1 ≤ δi < 2ν) die größte Wahrscheinlichkeit für Menge
der Mächtigkeit qi,
P(2ν - qi - 1 ≤ δi < 2ν) die größte Wahrscheinlichkeit für Menge 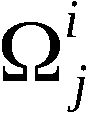 der
Mächtigkeit qi + 1.
Seien analog Pkt. 2 diese Wahrscheinlichkeiten mit π'i(p) bzw. π"i(p)
bezeichnet.
Wir betrachten die Abbildung δ : N(2ν) → N(2ν) (siehe Definition 3).
∀ l ∈ N(2ν) : δl = 2ν - 1 - l
und ‖δl‖ = ν - ‖l‖ (vergl. (3.4)).
Aus (3.5) folgt:
P(δi = l/p) = p‖l‖ qν-‖l‖
P(δi = l/p) = pν-‖l‖ q‖l‖
→ P(δi = l/p) = P(δi = 2ν - 1 - l/q) (∀ l ∈ N(2ν))
Verallgemeinert folgt daraus:
P(δi ≤ l/p) = P(2ν - 1 - l δ ≤i < 2ν/q) (3.9)
Damit folgt aus (3.8):
(3.10)
∀ p > ½: π'i(p) = P(δi < qi/p)
π"i(p) = P(δi < qi + 1 / q)
Völlig analoge Weise erhält man für den Fall p < ½
∀p < ½: P(½i < qi + 1 /p) ≥ πi,j(p) ≥ P(2ν - qi ≤ δi < 2ν / p)
sowie
(3.11)
∀p < ½: π'i(p) = P(δi < qi / q)
π"i(p) = P(δi < qi + 1 / p)
Ein Vergleich der Ausrücke (3.10) und (3.11) zeigt, daß
π'i und π"i als Funktion von p symmetrisch bezüglich p = ½
sind, d. h.
(3.12) π'i(p) = π'i(1 - p)
π"i(p) = π"i(1 - p)
Damit ist es ausreichend, die Untersuchungen auf den Fall p < ½
zu beschränken.
Mit der Formel (3.6) und
der
Mächtigkeit qi + 1.
Seien analog Pkt. 2 diese Wahrscheinlichkeiten mit π'i(p) bzw. π"i(p)
bezeichnet.
Wir betrachten die Abbildung δ : N(2ν) → N(2ν) (siehe Definition 3).
∀ l ∈ N(2ν) : δl = 2ν - 1 - l
und ‖δl‖ = ν - ‖l‖ (vergl. (3.4)).
Aus (3.5) folgt:
P(δi = l/p) = p‖l‖ qν-‖l‖
P(δi = l/p) = pν-‖l‖ q‖l‖
→ P(δi = l/p) = P(δi = 2ν - 1 - l/q) (∀ l ∈ N(2ν))
Verallgemeinert folgt daraus:
P(δi ≤ l/p) = P(2ν - 1 - l δ ≤i < 2ν/q) (3.9)
Damit folgt aus (3.8):
(3.10)
∀ p > ½: π'i(p) = P(δi < qi/p)
π"i(p) = P(δi < qi + 1 / q)
Völlig analoge Weise erhält man für den Fall p < ½
∀p < ½: P(½i < qi + 1 /p) ≥ πi,j(p) ≥ P(2ν - qi ≤ δi < 2ν / p)
sowie
(3.11)
∀p < ½: π'i(p) = P(δi < qi / q)
π"i(p) = P(δi < qi + 1 / p)
Ein Vergleich der Ausrücke (3.10) und (3.11) zeigt, daß
π'i und π"i als Funktion von p symmetrisch bezüglich p = ½
sind, d. h.
(3.12) π'i(p) = π'i(1 - p)
π"i(p) = π"i(1 - p)
Damit ist es ausreichend, die Untersuchungen auf den Fall p < ½
zu beschränken.
Mit der Formel (3.6) und  lassen sich
die Werte von π'i und π"i für konkrete n, ν, i sowie p
berechnen.
Analog zu Pkt. 2 definieren wir
P'(p) = π'1(p) · π'2(p) · … · π'n-1(p)
P"(p) = π"1(p) · π"2(p) · … · π"n-1(p)
sowie
lassen sich
die Werte von π'i und π"i für konkrete n, ν, i sowie p
berechnen.
Analog zu Pkt. 2 definieren wir
P'(p) = π'1(p) · π'2(p) · … · π'n-1(p)
P"(p) = π"1(p) · π"2(p) · … · π"n-1(p)
sowie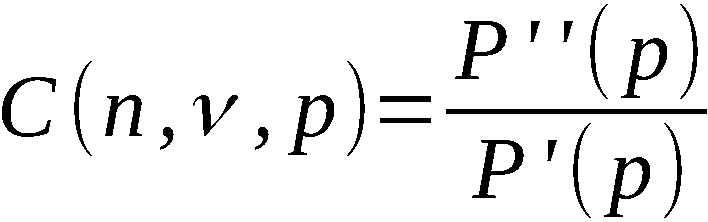
Es gilt P'(p) ≤ P({An-1 = PVn}) ≤ P"(p) (3.13)
Für die Anordnungen werden analog Pkt. 2 die Größen
͠P'(p), ͠P"(p) und ͠C(n,ν,k,p) ≤ C(n,ν,p) definiert.
Aus (3.12) folgt
C(n, ν, p) = C(n, ν, 1 - p).
Weiterhin betrachten wir

Auch hier gilt D(n, ν, p) = D(n, ν, 1 - p).
3.3. Numerische Aussagen
Nachfolgende Tabellen geben ein Überblick über einige konkrete Werte
für C(n, ν, p) und D(n, ν, p).
Die Berechnungen wurden mit dem programmierbaren Taschenrechner TI 59
ausgeführt. Die dabei verwendeten Programme beruhen auf den
Formeln (3.6) und (3.11).
Die Tabellen zeigen, daß für wachsende n die Werte C(n, ν, p)
für gleiche Werte p erheblich anwachsen (für festes ν).
Selbst unter der Annahme, daß p nur geringfügig von ½ abweicht
(für kryptologisch freigegebene Zufallsgeneratoren gilt i. A. 0,495 ≤ p ≤ 0,505)
erreicht C für größere n relativ hohe Werte, z. B. gilt für n = 32
C(32, 15, 0,495) = 12,66.
Die Werte zeigen auch, daß für p ≠ durch den Übergang von ν = 15 auf
ν = 31 keine entscheidende Veränderung von C erreicht wird (für die
betrachteten n), so ist C(32, 31, 0,495) = 12,46.
| Tabelle 3.1: Werte für C(n, 15, p) |
|---|
| p\n | 10 | 26 | 32 | 45 |
| 0,1 | 1,1558 · 1023 | | | |
| 0,4 | 16310,627 | 6,730 · 1016 | 1,664 · 1022 | 9,651 · 1034 |
| 0,45 | 121,465 | 2,126 · 108 | 9,998 · 1010 | 2,055 · 1017 |
| 0,49 | 2,607 | 46,095 | 157,912 | 2896,581 |
| 0,495 | 1,616 | 6,824 | 12,664 | 54,653 |
| 0,499 | 1,102 | 1,481 | 1,683 | 2,283 |
| 0,5 | 1,001649 | 1,010738 | 1,016212 | 1,032055 |
| Tabelle 3.2: Werte für C(n, 31, p) |
|---|
| p\n | 10 | 32 | 45 |
| 0,4 | 16 250,290 | | |
| 0,45 | 121,192 | 9,824 · 1010 | |
| 0,49 | 2,602 | 155,367 | 2807,574 |
| 0,495 | 1,613 | 12,461 | 52,965 |
| 0,499 | 1,100340 | 1,656 | 2,212 |
| 0,5 | 1,000 000 025 | 1,000 000 245 | 1,000 000 481 |
| Tabelle 3.3: Werte für D(n, 15, p) |
|---|
| p\n | 10 | 26 | 32 | 45 |
| 0,1 | 508 548,54 · 1/10! | | | |
| 0,4 | 72,074 · 1/10! | 2,912 · 107 · 1/26! | 7,753 · 109 · 1/32! | 3,551 · 1015 · 1/45! |
| 0,45 | 8,604 · 1/10! | 8502,698 · 1/26! | 158 263,78 · 1/32! | 1,509 · 108 · 1/45! |
| 0,49 | 0,606 · 1/10! | 5,646 · 1/26! | 11,237 · 1/32! | 50,659 · 1/45! |
| 0,495 | 0,270 · 1/10! | 1,599 · 1/26! | 2,538 · 1/32! | 6,334 · 1/45! |
| 0,499 | 0,0499 · 1/10! | 0,217 · 1/26! | 0,298 · 1/32! | 0,515 · 1/45! |
| 0,5 | 9,159 · 10-4 · 1/10! | 0,005 · 1/26! | 0,009 · 1/32! | 0,019 · 1/45! |
| Tabelle 3.4: Werte für D(n, 31, p) |
|---|
| p\n | 10 | 32 | 45 |
| 0,4 | 71,545 · 1/10! | | |
| 0,45 | 8,589 · 1/10! | 156 545,81 · 1/32! | |
| 0,49 | 0,604 · 1/10! | 11,125 · 1/32! | 49,710 · 1/45! |
| 0,495 | 0,268 · 1/10! | 2,506 · 1/32! | 6,198 · 1/45! |
| 0,499 | 0,049 · 1/10! | 0,287 · 1/32! | 0,486 · 1/45! |
| 0,5 | 1,626 · 10-8 · 1/10! | 1,605 · 10-7 · 1/32! | 4,815 · 10-7 · 1/45! |
3.4. Ergänzung zu Punkt 3.2. und 3.3
Ergänzend zu den in Punkt 3.2. hergeleiteten Abschätzungen
für die größte (P") und die kleinste (P') Wahrscheinlichkeit
der Erzeugung einer Permutation mittels APV sollen im
Falle p < ½ die exakten extremen Wahrscheinlichkeiten
berechnet und die betreffenden Permutationen angegeben
werden.
Sei im Folgenden stets p < ½:
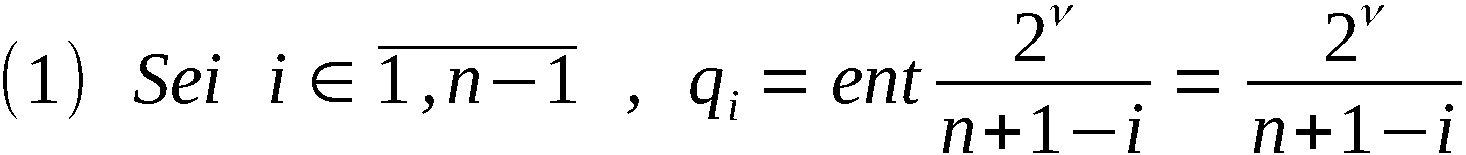
Dann gilt ∀ j ∈ 0, n-i:
 und aus (3.7.) folgt:
π'i,0(p) = P(δi < qi/p) ≥ πi,j(p) ≥ P(2ν - qi ≤ δi < 2ν/p) = πi, n-i(p)
D. h. π"i(p) > πi,0(p) ≥ πi,j(p) ≥ πi, n-i(p) = π'i(p) (3.14.)
und aus (3.7.) folgt:
π'i,0(p) = P(δi < qi/p) ≥ πi,j(p) ≥ P(2ν - qi ≤ δi < 2ν/p) = πi, n-i(p)
D. h. π"i(p) > πi,0(p) ≥ πi,j(p) ≥ πi, n-i(p) = π'i(p) (3.14.)

Es wird gezeigt, daß πi,0(p) = π"i(p) und πi, n-i(p) = π'i(p).
Sei j = 0

und mit (1.5.), (3.9.), (3.11.):
πi,0(p) = π"i(p) (3.15.)
Sei j = n-1.
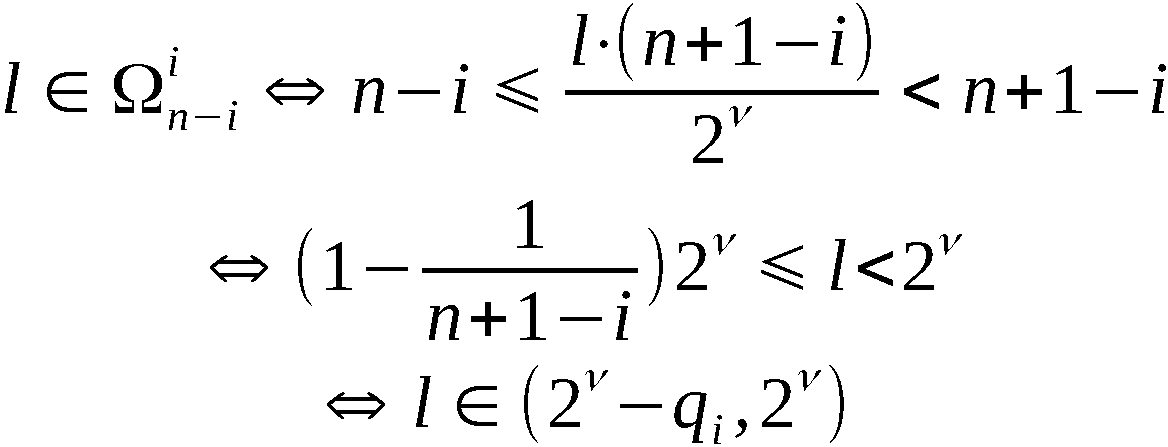
D. h. 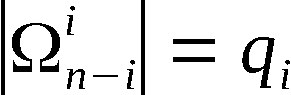 und aus (1.5.), (3.9.) und (3.11)
folgt
πi, n-i(p) = π'i(p) (3.16.)
Damit gilt ∀ p < ½
und aus (1.5.), (3.9.) und (3.11)
folgt
πi, n-i(p) = π'i(p) (3.16.)
Damit gilt ∀ p < ½
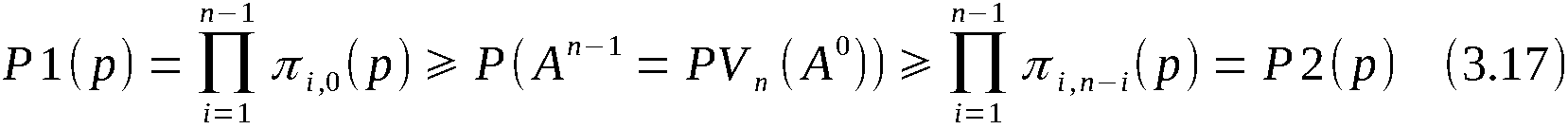
D. h., wenn A0 = (a1, …, an), wird die Permutation A0
mit der größten und die Permutationen (an, a1, a2, …, an-1)
mit der geringsten Wahrscheinlichkeit erzeugt.
Die numerischen Werte für P1, P2 und C = P1/P2
auf den nächsten Seiten wurden mit einem Programm
(MSG3) auf dem MRES berechnet.
Bemerkungen zum Fall p > ½:
Analog oben und mittels (3.9) erhält man leicht
folgende Beziehung:

D. h., daß die folgend berechneten numerischen Werte P1, P2, C auch
zur Einschätzung des APV bei p > ½ genutzt werden können
(bzgl. Pkt. 3.3. sind dies genauere Abschätzungen). (3.18) ist als
echte Ungleichung möglich - deshalb können keine den extremalen
Wkt. entsprechenden Permutationen angegeben werden.
| Tabelle 3.5. |
| N = 10 | P1 * N! | P2 * N! | C(N, 15, p) |
| 0,5 | 1,000 37 | 0,999 147 | 1,001 22 |
| 0,499 | 1,049 3 | 0,952 446 | 1,101 69 |
| 0,495 | 1,268 78 | 0,785 606 | 1,615 03 |
| 0,49 | 1,604 87 | 0,615 977 | 2,605 4 |
| 0,45 | 9,592 81 | 0,079 036 | 121,372 |
|
| N = 26 | P1 * N! | P2 * N! | C |
| 0,5 | 1,004 44 | 0,994 676 | 1,009 81 |
| 0,499 | 1,215 52 | 0,821 575 | 1,479 5 |
| 0,495 | 2,595 8 | 0,380 747 | 6,817 65 |
| 0,49 | 6,637 98 | 0,144 158 | 46,046 5 |
| 0,45 | 8483,92 | 0,000 039 | 212,154 · 106 |
|
| N = 32 | P1 * N! | P2 * N! | C |
| 0,5 | 1,007 02 | 0,992 827 | 1,014 29 |
| 0,499 | 1,295 59 | 0,771 258 | 1,679 83 |
| 0,495 | 3,530 22 | 0,279 317 | 12,638 8 |
| 0,49 | 12,208 8 | 0,077 483 | 157,567 |
| 0,45 | 157570 | 0,000 001 | 995,791 · 108 |
|
| N = 45 | P1 * N! | P2 * N! | C |
| 0,5 | 1,016 99 | 0,987 269 | 1,030 1 |
| 0,499 | 1,511 79 | 0,663 511 | 2,278 47 |
| 0,495 | 7,318 16 | 0,134 176 | 54,541 7 |
| 0,49 | 51,538 3 | 0,017 831 | 2890,23 |
| 0,45 | 150,244 · 106 | 733,917 · 106 | 204,715 · 1013 |
| |
| Tabelle 3.6. |
| N = 10 | P1 * N! | P2 * N! | C(N, 30, p) |
| 0,499 | 1,048 91 | 0,953 26 | 1,100 34 |
| 0,495 | 1,268 3 | 0,786 287 | 1,613 03 |
| 0,49 | 1,604 25 | 0,616 521 | 2,602 11 |
|
| N = 26 | P1 * N! | P2 * N! | C |
| 0,499 | 1,210 17 | 0,825 967 | 1,465 15 |
| 0,495 | 2,584 52 | 0,382 779 | 6,752 |
| 0,49 | 6,609 68 | 0,144 926 | 45,607 4 |
|
| N = 32 | P1 * N! | P2 * N! | C |
| 0,499 | 1,286 56 | 0,776 823 | 1,656 19 |
| 0,495 | 3,505 74 | 0,281 327 | 12,461 4 |
| 0,49 | 12,124 6 | 0,078 039 | 155,366 |
|
| N = 45 | P1 * N! | P2 * N! | C |
| 0,499 | 1,486 62 | 0,672 064 | 2,212 02 |
| 0,495 | 7,198 15 | 0,135 05 | 52,964 6 |
| 0,49 | 50,709 1 | 0,018 061 | 2807,56 |
|
| N = 100 | P1 * N! | P2 * N! | C |
| 0,499 | 3,023 47 | 0,329 935 | 9,163 84 |
| 0,495 | 246,681 | 0,003 816 | 64643,9 |
| 0,49 | 57354,2 | 0,000 013 | 441,186 · 107 |
|
| N = 150 | P1 * N! | P2 * N! | C |
| 0,499 | 6,208 36 | 0,160 435 | 38,697 1 |
| 0,495 | 8870,87 | 0,000 102 | 868,152 · 105 |
| 0,49 | 714,718 · 105 | 0,896 891 · 10-08 | 796,884 · 1013 |
|
| N = 200 | P1 * N! | P2 * N! | C |
| 0,499 | 13,539 9 | 0,073 439 | 184,369 |
| 0,495 | 430361 | 0,000 002 | 213,168 · 109 |
| 0,49 | 161,368 · 109 | 0,335 332 · 10-11 | 481,219 · 1020 |
Bemerkung:
Der APV ist auf EDVA so realisiert, daß für n > 45 zur
Bildung der δi automatisch je ν = 30 Bit
(2 Worte zu 15 Bit) verwendet werden.
| Tabelle 3.7. |
| N = 10 | P1 * N! | P2 * N! | C(N, 6, p) |
| 0,5 | 1,362 77 | 0,713 804 | 1,909 16 |
| 0,499 | 1,427 21 | 0,679 902 | 2,099 14 |
| 0,495 | 1,715 11 | 0,559 022 | 3,068 06 |
| 0,49 | 2,152 9 | 0,436 555 | 4,931 57 |
| 0,45 | 12,143 2 | 0,054 094 | 224,481 |
|
| N = 26 | P1 * N! | P2 * N! | C |
| 0,5 | 6,421 54 | 0,037 372 | 171,825 |
| 0,499 | 7,693 56 | 0,030 757 | 250,139 |
| 0,495 | 15,789 9 | 0,014 05 | 1123,78 |
| 0,49 | 38,451 | 0,005 226 | 7356,89 |
| 0,45 | 34248,6 | 0,000 001 | 269,541 · 108 |
|
| N = 10 | P1 * N! | P2 * N! | C(N, 8, p) |
| 0,5 | 1,089 1 | 0,924 235 | 1,178 38 |
| 0,499 | 1,141 99 | 0,881 072 | 1,29 613 |
| 0,495 | 1,379 02 | 0,726 864 | 1,897 21 |
| 0,49 | 1,741 45 | 0,570 067 | 3,054 82 |
| 0,45 | 10,286 7 | 0,073 405 | 140,135 |
|
| N = 26 | P1 * N! | P2 * N! | C |
| 0,5 | 2,033 61 | 0,580 625 | 3,502 46 |
| 0,499 | 2,451 79 | 0,479 455 | 5,113 71 |
| 0,495 | 5,158 81 | 0,221 982 | 154,281 |
| 0,49 | 12,953 6 | 0,083 96 | 23,239 7 |
| 0,45 | 14474,5 | 0,000 023 | 622,109 · 106 |
|
| N = 10 | P1 * N! | P2 * N! | C(N, 10, p) |
| 0,5 | 1,017 7 | 0,976 786 | 1,041 88 |
| 0,499 | 1,067 39 | 0,931 102 | 1,146 38 |
| 0,495 | 1,290 25 | 0,767 908 | 1,680 22 |
| 0,49 | 1,631 38 | 0,602 009 | 2,709 89 |
| 0,45 | 9,720 86 | 0,077 144 | 126,008 |
|
| N = 26 | P1 * N! | P2 * N! | C |
| 0,5 | 1,152 42 | 0,841 156 | 1,370 05 |
| 0,499 | 1,393 58 | 0,694 749 | 2,005 87 |
| 0,495 | 2,967 3 | 0,321 938 | 9,216 99 |
| 0,49 | 7,560 46 | 0,121 883 | 62,030 6 |
| 0,45 | 9401,96 | 0,000 033 | 277,704 · 106 |
Die Tabellen 3.5 bis 3.7 zeigen den Einfluß von ν auf
die hier berechneten Wahrscheinlichkeiten. Je kleiner
(2ν - n) um so größer wird C (d. h. extremalen Wkt.
weichen von Gleichverteilung ab).
4. Bistochastische Matrizen
Sei die Menge aller Si ∈ S(M), |M| = n,
in irgendeiner Weise geordnet.
(Nachtrag: Eine Möglichkeit der Ordnung der Elemente von S(M)
bietet der Algorithmus P, /8/, S. 80)
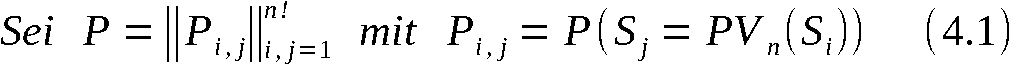
Zum Ergebnis {Sj = PVn(Si)} gehört laut Definition des APV,
vergl. Bl. 6, die Ereignisfolge  mit A0 = Si und
An-1 = Sj (eed. Zuordnung, vgl. Bl. 5).
mit A0 = Si und
An-1 = Sj (eed. Zuordnung, vgl. Bl. 5).

Satz
P und P(k) sind bistochastische Matrizen.
Beweis:
 wobei {Ak = St / Ak-1 = Ss} entspricht einem Ereignis {ɳk = js,t}
(d. h. St entsteht aus Ss durch Vertauschung der k-ten und
(k+js,t)-ten Elemente).
Offensichtlich gilt
wobei {Ak = St / Ak-1 = Ss} entspricht einem Ereignis {ɳk = js,t}
(d. h. St entsteht aus Ss durch Vertauschung der k-ten und
(k+js,t)-ten Elemente).
Offensichtlich gilt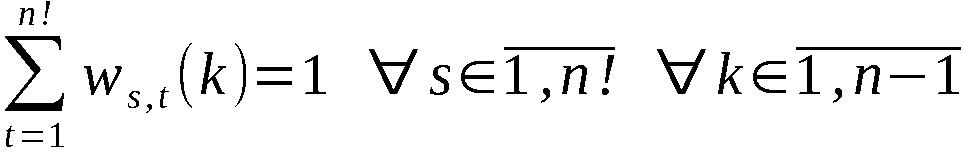
und
{Ak = St / Ak-1 = Ss} ←→ {ɳk = js,t} = {ɳk = jt,s} ←→ {Ak = Ss / Ak-1 = St}.
D. h. ∀ k ∈ 1,n-1 W(k) symmetrische und damit
bistochastische Matrizen.
Offensichtlich sind P(n-1) = P und P(1) = W(1).
Es sei zu berechnen pi,r(k+1).
Nach dem Satz über die vollständige Wahrscheinlichkeit
gilt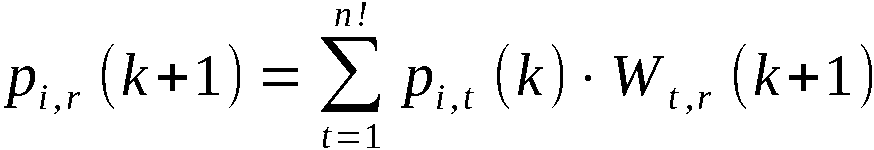 .
.
D. h. P(k+1) = P(k) · W(k+1)
und damit ist
P(k) = W(1) · W(2) · … · W(k)
Da die Multiplikation von bistochastischen Matrizen
stets bistochastische Matrizen ergibt, ist damit die
Behauptung bewiesen.
Teil II
Erzeugung von Folgen von Permutation oder Anordnungen mittels des APV
Inhalt:
1. Einleitung
2. Variante 1 - Folgenerzeugung bei fester Ausgangspermutation
2.1. Folgen von Permutation
2.2. Folgen von Anordnungen
3. Variante 2 - Verwendung der Ergebnispermutation als
Ausgangspermutation
3.1. Folgen von Permutationen
3.2. Folgen von Anordnungen
1. Einleitung
Aufbauend auf den Ergebnissen aus Teil I zu den Eigenschaften
des APV bei einmaliger Anwendung sollen im Teil II die Eigen-
schaften des APV bei der Erzeugung von Folgen von Permutationen
(Xi)i bzw. Anordnungen 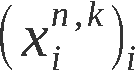 untersucht werden.
Die Untersuchungen werden nur für den allgemeinen, d. h prak-
tisch interessanten Fall durchgeführt (analog Teil I, Pkt. 3.).
Es werden mathematisch-statistische Eigenschaften zweier Vari-
anten der Folgen-Erzeugung untersucht.
Mit der Verwendung von Ergebnissen aus Teil I werden i. d.
auch die entsprechenden Bezeichnungen übernommen. Weitere
grundlegende Bezeichnungen sind:
(Xi)i - Folge von Permutationen des Grades n als
Realisierung des APV
untersucht werden.
Die Untersuchungen werden nur für den allgemeinen, d. h prak-
tisch interessanten Fall durchgeführt (analog Teil I, Pkt. 3.).
Es werden mathematisch-statistische Eigenschaften zweier Vari-
anten der Folgen-Erzeugung untersucht.
Mit der Verwendung von Ergebnissen aus Teil I werden i. d.
auch die entsprechenden Bezeichnungen übernommen. Weitere
grundlegende Bezeichnungen sind:
(Xi)i - Folge von Permutationen des Grades n als
Realisierung des APV
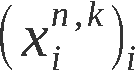 - Folge von Anordnungen von k aus n Elementen, erzeugt
durch den APV
- Folge von Anordnungen von k aus n Elementen, erzeugt
durch den APV
 - Menge aller Anordnungen von k aus n Elementen
P', P", ͠P', ͠P", P1, P2
- Grenzen/Abschätzungen für die Wahrscheinlichkeit der
Erzeugung von Permutationen und Anordnungen nach dem
APV, siehe Teil I.
2. Variante 1 - Folgenerzeugung bei fester Ausgangspermutation
2.1. Folgen von Permutationen
Die Folge der Permutationen
- Menge aller Anordnungen von k aus n Elementen
P', P", ͠P', ͠P", P1, P2
- Grenzen/Abschätzungen für die Wahrscheinlichkeit der
Erzeugung von Permutationen und Anordnungen nach dem
APV, siehe Teil I.
2. Variante 1 - Folgenerzeugung bei fester Ausgangspermutation
2.1. Folgen von Permutationen
Die Folge der Permutationen  wird nach der
Variante 1 durch mehrfache Anwendung des APV auf eine fest
vorgegebene Ausgangspermutation X0 erzeugt,
d. h. ∀ i ∈ 1,m : Xi = PVm(X0).
Aus ∀ Sj ∈ S(M), ∀ i ∈ 1,m:
E(Sj) = m · P(PVm(X0) = Sj).
Da gemäß Teil I bei gegebenem p (s. Bl. 12):
∀ Sj ∈ S(M) P2 ≤ P(PVn(X0) = Sj) ≤ P1
gilt
m · P2 ≤ E(Sj) ≤ m · P1 (2.1.)
Analog Teil I wird definiert
wird nach der
Variante 1 durch mehrfache Anwendung des APV auf eine fest
vorgegebene Ausgangspermutation X0 erzeugt,
d. h. ∀ i ∈ 1,m : Xi = PVm(X0).
Aus ∀ Sj ∈ S(M), ∀ i ∈ 1,m:
E(Sj) = m · P(PVm(X0) = Sj).
Da gemäß Teil I bei gegebenem p (s. Bl. 12):
∀ Sj ∈ S(M) P2 ≤ P(PVn(X0) = Sj) ≤ P1
gilt
m · P2 ≤ E(Sj) ≤ m · P1 (2.1.)
Analog Teil I wird definiert  Offensichtlich ist
Offensichtlich ist  D. h. das Verhältnis größter Erwartungswert zu kleinstem bleibt
so wie im Falle einer einmaligen Anwendung des APV (m = 1).
Zur Einschätzung der Variante 1 auf der Basis von (2.1.) und
(2.2.) können somit unmittelbar die numerischen Werte aus
Teil I, Pkt. 3.3. oder 3.4. genutzt werden.
2.2. Folgen von Anordnungen
Die Folge von Anordnungen
D. h. das Verhältnis größter Erwartungswert zu kleinstem bleibt
so wie im Falle einer einmaligen Anwendung des APV (m = 1).
Zur Einschätzung der Variante 1 auf der Basis von (2.1.) und
(2.2.) können somit unmittelbar die numerischen Werte aus
Teil I, Pkt. 3.3. oder 3.4. genutzt werden.
2.2. Folgen von Anordnungen
Die Folge von Anordnungen  wird nach der Variante I
durch mehrfache Anwendung des APV auf eine fest vorgegebene
Ausgangspermutation X0 erzeugt,
wird nach der Variante I
durch mehrfache Anwendung des APV auf eine fest vorgegebene
Ausgangspermutation X0 erzeugt,

Völlig analog zu Punkt 2.1. lassen sich für die mathematische
Erwartung E des Auftretens einer Anordnung 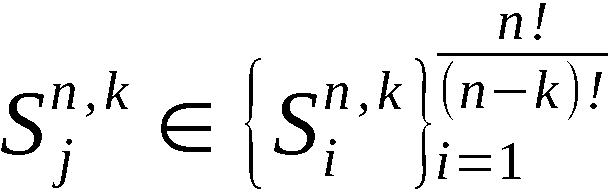 folgende Beziehungen herleiten:
folgende Beziehungen herleiten:

wobei (vgl. Teil I, Bl. 40) ͠C(n, ν, k, p) ≤ C(n, ν, p).
3. Variante 2 - Verwendung der Ergebnispermutation als
Ausgangspermutation
3.1. Folgen von Permutationen
Nach der Variante 2 wird durch den APV die Folge der Permu-
tationen 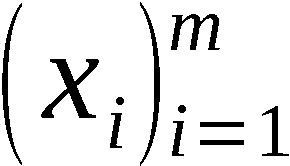 erzeugt, in dem die jeweils im (i-1)ten Schritt
erzeugte EP Xi-1 als APV zur
Erzeugung der Permutation Xi dient. D. h.
∀ i ∈ 1,m : Xi = PVn (Xi-1)
wobei X0 eine vorgegebene AP.
Für jeden Schritt i gelten die Abschätzungen mit P1 und P2
aus Teil I (unabhängig von konkreter AP). Deshalb gelten auch
hier die Beziehungen (2.1.) und (2.2.) der Variante 1 der
Folgenerzeugung.
Für die Variante 2 der Folgenerzeugung können jedoch mittels
der Theorie der Markow'schen Ketten noch mehr qualitative
Aussagen bzgl. der Verteilung der erzeugten Permutationen
getroffen werden.
Der Prozeß der Folgenerzeugung nach Variante 2 wird durch
folgende Markow'sche Ketten dargestellt.
S(M) - Menge der Zustände der Kette,
X0 ∈ S(M) - beliebiger Anfangszustand;
- Der Übergang von einem Zustand zum anderen wird durch den
APV realisiert.
Damit sind die Übergangswahrscheinlichkeiten im l-ten Schritt
definiert durch
pr,t = P(Xl = St / Xl-1 = Sr) = P(St = PVn(Sr))
D. h. die Übergangswahrscheinlichkeit pr,t sind
unabhängig vom Schritt l und es liegt eine homogene Markow'sche
Kette vor.
erzeugt, in dem die jeweils im (i-1)ten Schritt
erzeugte EP Xi-1 als APV zur
Erzeugung der Permutation Xi dient. D. h.
∀ i ∈ 1,m : Xi = PVn (Xi-1)
wobei X0 eine vorgegebene AP.
Für jeden Schritt i gelten die Abschätzungen mit P1 und P2
aus Teil I (unabhängig von konkreter AP). Deshalb gelten auch
hier die Beziehungen (2.1.) und (2.2.) der Variante 1 der
Folgenerzeugung.
Für die Variante 2 der Folgenerzeugung können jedoch mittels
der Theorie der Markow'schen Ketten noch mehr qualitative
Aussagen bzgl. der Verteilung der erzeugten Permutationen
getroffen werden.
Der Prozeß der Folgenerzeugung nach Variante 2 wird durch
folgende Markow'sche Ketten dargestellt.
S(M) - Menge der Zustände der Kette,
X0 ∈ S(M) - beliebiger Anfangszustand;
- Der Übergang von einem Zustand zum anderen wird durch den
APV realisiert.
Damit sind die Übergangswahrscheinlichkeiten im l-ten Schritt
definiert durch
pr,t = P(Xl = St / Xl-1 = Sr) = P(St = PVn(Sr))
D. h. die Übergangswahrscheinlichkeit pr,t sind
unabhängig vom Schritt l und es liegt eine homogene Markow'sche
Kette vor.

Wie im Teil I Pkt. 4 nachgewiesen, ist P eine bistochastische
Matrix.
Die Übergangsmatrix über m Schritte 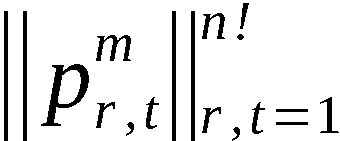 mit
mit  läßt sich im vorliegenden Fall einer homogenen
Markow'schen Kette /6, S.215/, /7, S.393/ als Potenz von P
berechnen:
läßt sich im vorliegenden Fall einer homogenen
Markow'schen Kette /6, S.215/, /7, S.393/ als Potenz von P
berechnen:

In Teil I wurde gezeigt, daß
∀ (r,t) ∈ (1,n!)2 : min pr,t ≥ P2 > 0.
Damit sind für die vorliegende homogene Markow'sche Kette mit
endlich vielen Zuständen alle Voraussetzungen des Ergodensatzes
in /6, S.216 ff/ (ebenfalls in /7, S.395/)
erfüllt, und es gilt:
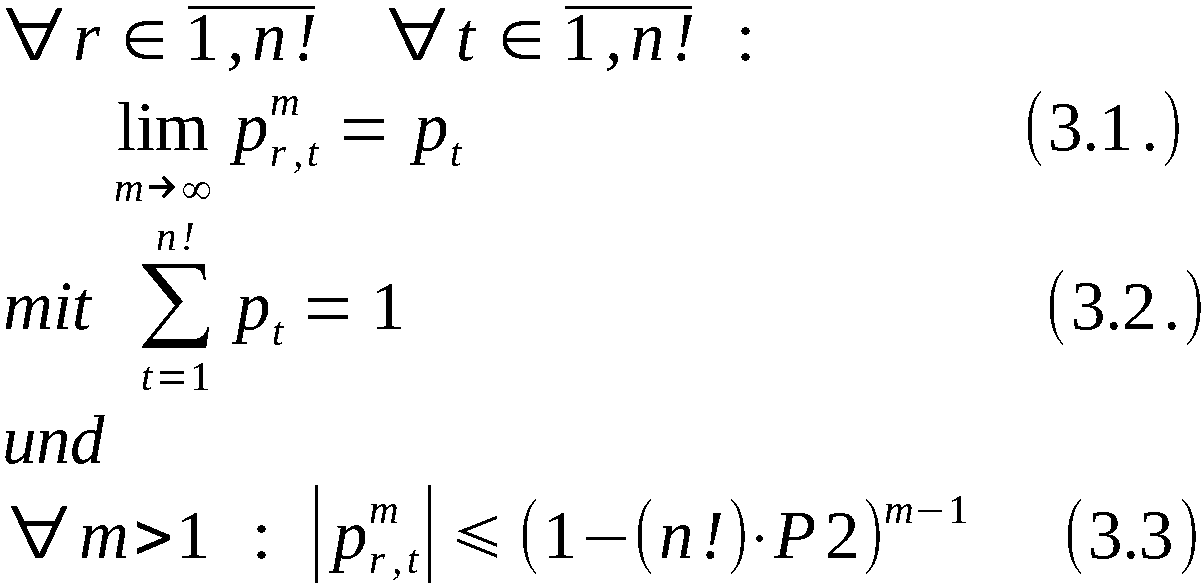
Da P und damit auch Pm bistochastisch, folgt aus
(3.1.) und (3.2.) (vgl. auch /7, S.398/).

‖ D. h. für jede beliebige Ausgangspermutation sind
‖ die nach der Variante 2 mit dem APV erzeugten Per-
‖ mutationen asymtomatisch gleichverteilt.
Mit Hilfe von (3.3.) können die Abschätzungen (2.1.) und (2.2.)
für die mathematische Erwartung des Auftretens einer Permutation
Sj ∈ S(M) in der nach der Variante 2 erzeugten
Folge von Permutationen verbessert werden.
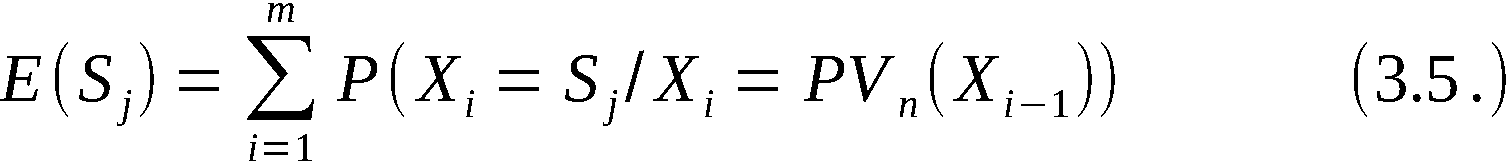
Nach Teil I gilt:
P2 ≤ P(Xi = Sj / Xi = PVn(Xi-1)) ≤ P1 (3.6.)
und wegen (3.3.)
∀ m > l0 (zur Wahl von l0 s. u.):
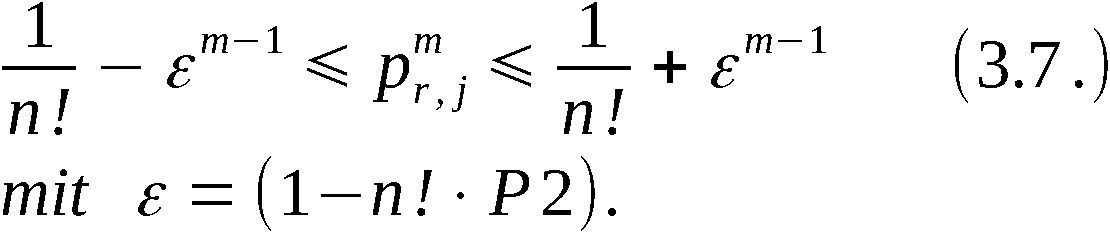
E(Sj) kann dann wie folgt berechnet und abgeschätzt werden:
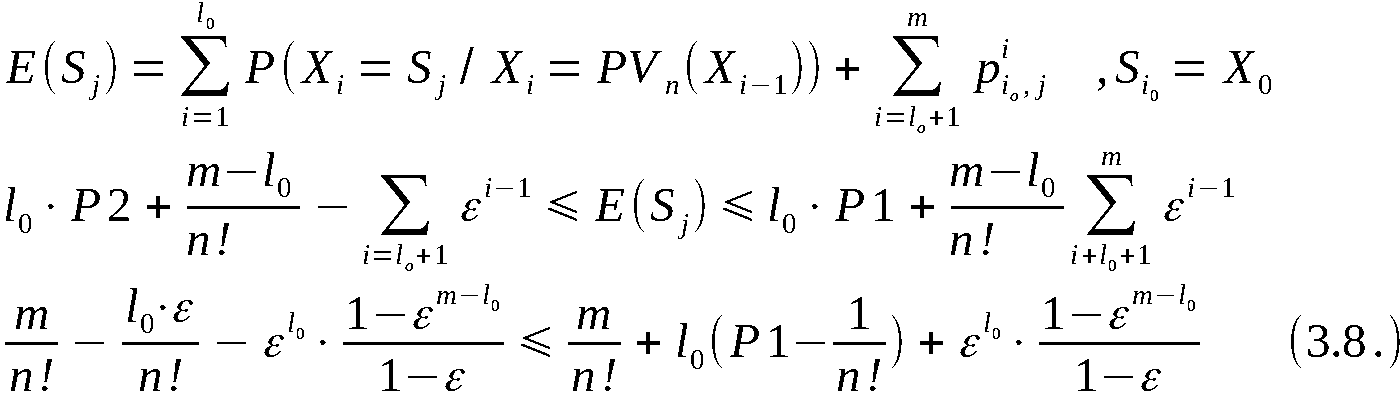
Sei C2(n, ν, p, l0) der Quotient aus oberer Grenze
durch untere Grenze in (3.8.).
Bei der Berechnung folgender Tabelle wurde l0 jeweils
so gewählt, daß die Nutzung von (3.7.) gegenüber (3.6.) eine
Verbesserung in der Abschätzung in (3.8.) ergab.
| m | C2(10, 15, 0.495, 10) | C2(26, 15, 0.495, 130) | C2(26, 15, 0.499, 35) |
|---|
| 20 | 1,395 | | |
| 30 | 1,248 | | |
| 50 | 1,142 | | 1,28 |
| 100 | 1,069 | | 1,13 |
| 150 | | 5,22 | |
| 200 | 1,034 | 3,44 | 1,06 |
| 500 | 1,013 | 1,69 | 1,025 |
| 1000 | | 1,32 | 1,012 |
| C1(n, 15, p) | 1,615 | 6,82 | 1,48 |
3.2. Folgen von Anordnungen
Nach der Variante 2 wird durch den APV die Folge der Anord-
nungen  erzeugt, indem die jeweils im (i-1)-ten Schritt
faktisch erzeugte Ergebnispermutation (Yi-1) als
Ausgangspermutation zur Erzeugung der Anordnung
erzeugt, indem die jeweils im (i-1)-ten Schritt
faktisch erzeugte Ergebnispermutation (Yi-1) als
Ausgangspermutation zur Erzeugung der Anordnung  dient.
D. h.
dient.
D. h. 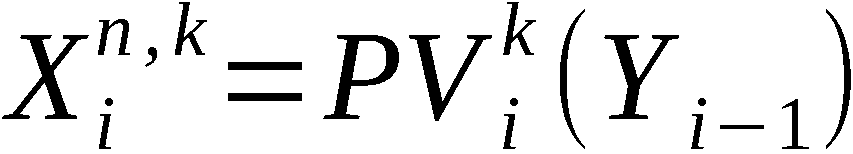 und gleichzeitig wird durch die k Vertauschungen
in Yi-1 (gemäß
und gleichzeitig wird durch die k Vertauschungen
in Yi-1 (gemäß 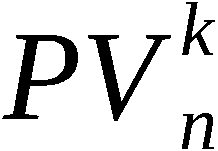 )
eine EP Yi erzeugt. Es gilt
)
eine EP Yi erzeugt. Es gilt
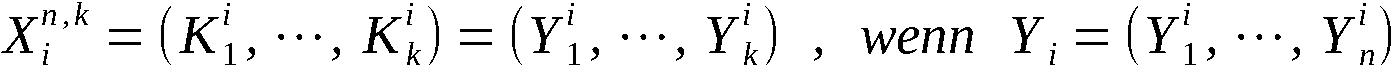
Es soll auch hier analog Pkt. 3.1. das Grenzverhalten der
Verteilung der so erzeugten Anordnungen untersucht werden.
Betrachten wir zunächst die Folge der nach dem APV (mit k Ver-
tauschungen) intern erzeugten Folge der Permutationen  .
Wie im Pkt. 3.1. soll der Prozeß der Folgenerzeugung als homo-
gene Markow'sche Kette mit der Übergangsmatrix
P(k) = ‖pr,t(k)‖ , siehe Teil I (4.2.),
Dargestellt sein. Analog Pkt 3.1. erhält man für die Übergangs-
matrix über m Schritte
.
Wie im Pkt. 3.1. soll der Prozeß der Folgenerzeugung als homo-
gene Markow'sche Kette mit der Übergangsmatrix
P(k) = ‖pr,t(k)‖ , siehe Teil I (4.2.),
Dargestellt sein. Analog Pkt 3.1. erhält man für die Übergangs-
matrix über m Schritte
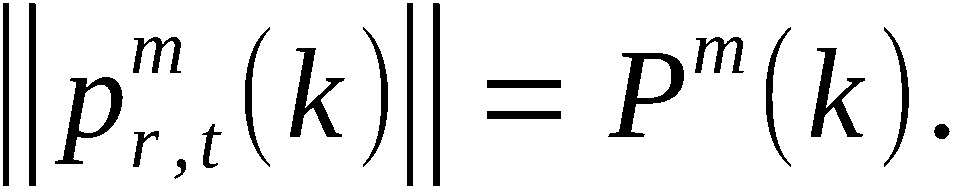
Da hier in einem Schritt nur k Vertauschungen durchgeführt
werden (d. h.  EP möglich sind) gibt es offensichtlich
(r,t) ∈ (1,n!)2 für die pr,t(k) = 0.
Es soll deshalb zunächst gezeigt werden, daß
EP möglich sind) gibt es offensichtlich
(r,t) ∈ (1,n!)2 für die pr,t(k) = 0.
Es soll deshalb zunächst gezeigt werden, daß

D. h., nach m ≥ m0 Schritten des vorgegebenen Algo-
rithmus (mit k Vertauschungen) könnte dann jede EP S't
aus jeder AP Sr erzeugt werden.

Folgende Folge von 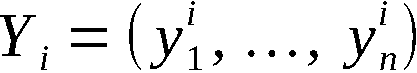 ist nach der Variante 2
der Folgenerzeugung für jede AP Sr realisierbar:
ist nach der Variante 2
der Folgenerzeugung für jede AP Sr realisierbar:

Mit den Ergebnissen von Teil I folgt dann

Damit sind auch für die homogene Markow'sche Kette alle Vor-
aussetzungen des Ergodensatzes /6/ erfüllt und es gilt
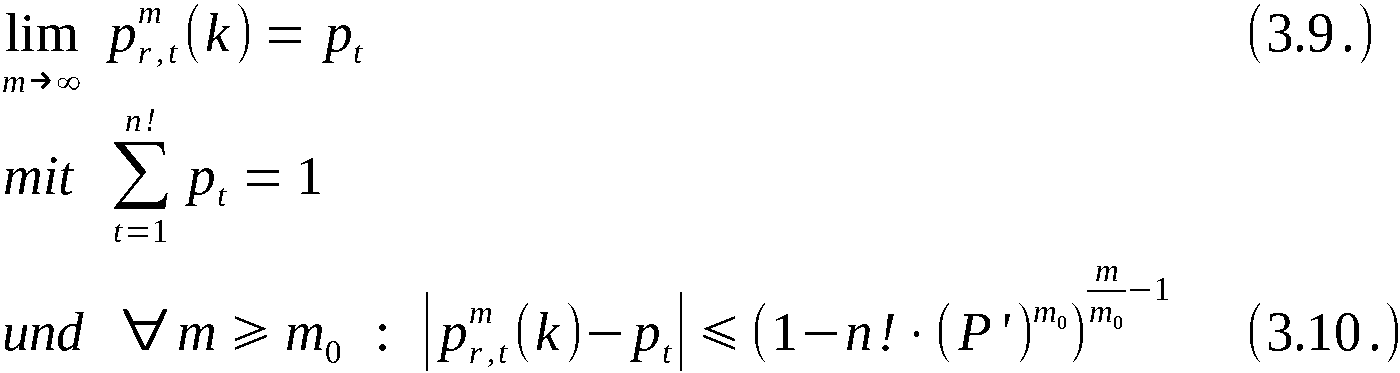
Da auch hier P(k) bistochastisch, vgl. Teil I, Pkt. 4.,
gilt ebenfalls

D. h. nach der Variante 2 der Erzeugung von Folgen von Anord-
nungen sind die intern erzeugten Permutationen asymtomatisch
gleichverteilt. Da aber jeder der  Anordnungen
Anordnungen  genau (n-k)! intern erzeugte Permutationen entsprechen, sind
auch die Anordnungen bei beliebiger AP asymptomatisch gleich-
verteilt, d. h.
genau (n-k)! intern erzeugte Permutationen entsprechen, sind
auch die Anordnungen bei beliebiger AP asymptomatisch gleich-
verteilt, d. h.
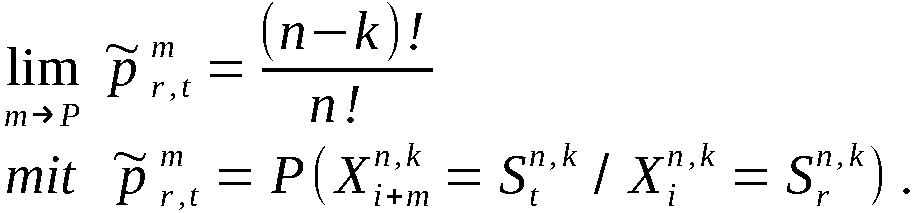
Teil III
Anwendung des APV zur Chiffriermittelproduktion
Inhalt:
1. Einleitung
2. Widerstand gegen Angriffe des Gegners
2.1. Untersuchungsgegenstand
2.2. Voraussetzungen
2.3. Die Totale Probiermethode
2.4. Effektivierung der Totalen Probiermethode
2.5. Untermenge wahrscheinlichster Permutationen
2.6. Rekonstruierbarkeit einzelner Stellen der Permutation
3. Anwendungsbedingungen
3.1. Anforderungen an die Zufallsfolge
3.2. Wahl des Parameters ν
3.3. Erzeugung von Folgen von Permutationen und Anordnungen
3.4. Kryptologische und programmtechnische Kontrollen
4. Zusammenfassung
1. Einleitung
Ausgehend von den in den Teilen I und II enthaltenen theoretischen
Grundlagen und Ergebnissen beschäftigt sich Teil 111 des vor-
liegenden Dokumentes mit kryptologischen Wertungen der Reali-
sierung des APV auf EDVA (einschließlich Mikrorechner) zur Pro-
duktion von Chiffriermitteln auf der Basis von zufälligen
Permutationen/Anordnungen.
Für die Praxis der Erzeugung, Verteilung und Anwendung solcher
Chiffriermittel kann als typisch angenommen werden, daß eine
Schlüsselserie als Einheit erzeugt, verteilt und angewendet
wird. Diese Einheit besteht aus h Permutationen n-ten Grades
bzw. k-Anordnungen. (Beispiele: h = 30 oder h = 31-Tagesschlüs-
sel, n = 10, n = 26-Ziffern- bzw. Buchstabenmischalphabete)
Zur Einschätzung der kryptologischen Qualität der Schlüssel-
serie wird die Abweichung vom Modell der Unabhängigen gleich-
wahrscheinlichen Auswahl von h Permutationen/Anordnungen aus
der Menge der möglichen Permutationen/Anordnungen betrachtet
(Abweichung vom "idealen Zufall").
Im Punkt III/2 werden mögliche Angriffe des Gegners untersucht,
die sich aus den in den Teilen I und II beschriebenen Eigen-
schaften der Realisierung des APV auf EDVA und den daraus resul-
tierenden Abweichungen vom "idealen Zufall" ergeben.
Punkt III/3 faßt die Anwendungsbedingungen zusammen, die sich
für die Anwendung des APV zur Produktion von Chiffriermitteln
ergeben.
Ausgangspunkt ist, daß APV als Unterprogramm auf EDVA ent-
sprechend Definition in der Einleitung, Punkte 3. und 6.,
realisiert wird.
Die Anwendungsbedingungen enthalten alle grundsätzlichen Forde-
rungen (einschließlich bestimmter technologischer Aspekte), die
notwendig sind, um eine hohe kryptologische Qualität der Pro-
duktion von Chiffriermitteln auf EDVA mit APV als Unterprogramm
zu gewährleisten.
Gleichzeitig wird eine kritische Wertung der derzeitigen Reali-
sierung entsprechender Programme zur Mittelproduktion auf der
EDVA PRS 4000 der Abteilung XI vorgenommen.
2. Widerstand gegen Angriffe des Gegners
2.1. Untersuchungsgegenstand
Gegenstand der Untersuchungen in diesem Abschnitt sind solche
Angriffe des Gegners auf Chiffrierverfahren, in denen mit APV
erzeugte Permutationen oder Anordnungen als Schlüsselkompo-
nenten angewendet werden, die sich auf die in den Teilen I und
II dieses Dokuments herausgearbeiteten Eigenschaften von
Realisierungen des APV beziehen. Insbesondere geht es dabei
um solche Angriffe, die sich auf die Abweichung der Verteilung
der mit APV erzeugten Permutationen/Anordnungen von der Gleich-
verteilung stützen. Angriffe, die sich aus dem konkret verwen-
deten Chiffrierverfahren ergeben, wie z. B. die Analyse von
Sprechtafeln, das Ausnutzen schlüsselgleicher Texte bzw. von
Geheimtext-Klartext-Paaren, sind nicht Gegenstand der vor-
liegenden Untersuchungen, da für solche Angriffe die Tatsache,
daß die als Schlüsselmittel verwendeten Permutationen/Anord-
nungen mit APV erzeugt wurden, nicht relevant ist.
2.2. Voraussetzungen
Für die folgenden Betrachtungen wird angenommen, daß dem Gegner
bekannt sei:
- der Algorithmus der Erzeugung von Permutationen/Anordnungen
in seiner konkreten Anwendung für die Erzeugung von Folgen
von Permutationen/Anordnungen
d. h. APV, Variante 1 oder 2 (vgl. Teil II)
- die Ausgangspermutation X0(für Variante I)
bzw. Xi als Ausgangspermutation für die Erzeugung von Xi+1
(für Variante 2)
- Aussagen zur Qualität der Zufallsquelle,
insbesondere Aussagen zur Wahrscheinlichkeit p für das Auf-
treten der 1 in der für die Bildung der Zahlenfolge (δi)i
verwendeten Bitfolge, vgl. Bl. 12
(Bereits mit Aussagen wie "p < ½" bzw. "p > ½" sind gewisse
Ansätze möglich!).
Mögliche weitere Aussagen zur Zufallsquelle (Abhängigkeiten,
zeitliche Schwankungen) werden hier unter Verweis auf Punkt 6
der Einleitung nicht näher betrachtet.
Es ist klar, daß diese Bedingungen in ihrer Gesamtheit kaum
praktisch erfüllbar sind - der Gegner müßte schon außergewöhn-
lich hervorragende Möglichkeiten zur Aufklärung der Mittelpro-
duktion haben.
2.3. Die Totale Probiermethode
Die Totale Probiermethode TPM besteht darin, daß durch die
systematische Überprüfung aller möglichen Permutationen oder
Anordnungen genau die als Schlüsselkomponente verwendete Per-
mutation oder Anordnung herausgefunden wird (mögliche Äquiva-
lenzen ,sollen hier nicht betrachtet werden). Voraussetzung
ist, daß alle Permutationen eines gegebenen Grades n vorliegen
bzw. erzeugt werden können.
Diese Möglichkeit bietet z. B. der Algorithmus P /8, S. 80/.
Die TPM führt in jedem Falle nach n! (für Permutationen) bzw.
 (für k-Anordnungen) Schritten zum Erfolg.
Für solche n und k, für die n! bzw.
(für k-Anordnungen) Schritten zum Erfolg.
Für solche n und k, für die n! bzw.  in für EDV-An-
wendungen realer Größenordnungen liegt, kann deshalb angenom-
men werden, daß der Gegner mit TPM zum Erfolg kommt, unab-
hängig von der konkreten Art der Erzeugung der Permutationen
der Anordnungen.
Da 10! = 3 628 800, beschränken wir alle folgenden Betrachtungen
auf n ≥10, da für n <10 TPM in jedem Falle anwendbar ist.
Die untere Grenze für solche Größenordnungen, für die TPM unter
heutigen Bedingungen real anwendbar ist, muß bei etwa 106 - 108
angenommen werden.
Für Anordnungen mit n ≥ 10 ist jeweils konkret für gegebenes k
die Größe von
in für EDV-An-
wendungen realer Größenordnungen liegt, kann deshalb angenom-
men werden, daß der Gegner mit TPM zum Erfolg kommt, unab-
hängig von der konkreten Art der Erzeugung der Permutationen
der Anordnungen.
Da 10! = 3 628 800, beschränken wir alle folgenden Betrachtungen
auf n ≥10, da für n <10 TPM in jedem Falle anwendbar ist.
Die untere Grenze für solche Größenordnungen, für die TPM unter
heutigen Bedingungen real anwendbar ist, muß bei etwa 106 - 108
angenommen werden.
Für Anordnungen mit n ≥ 10 ist jeweils konkret für gegebenes k
die Größe von  einzuschätzen.
Zur Illustration seien hier einige Werte für n = 26 angeführt:
einzuschätzen.
Zur Illustration seien hier einige Werte für n = 26 angeführt:
| k | 2 | 5 | 10 | 15 | 20 | 25 |
| n! | 650 | 7,9·106 | 1,9·1013 | 1019 | 5,6·1023 | 4·1026 = 26! |
| (n-k)! |
Offensichtlich kann für kleine k immer davon ausgegangen werden,
daß TPM anwendbar ist. Speziell gilt das für k ≤ 4, wenn
n ≤ 100.
Zur Vereinfachung der weiteren Darlegungen betrachten wir je-
weils die Ergebnispermutation nach k Schritten anstatt der kon-
kreten k-Anordnung, um die Untersuchungen auf Permutationen be-
schränken zu können.
Für konkrete n und k lassen sich alle numerischen Berechnungen
der folgenden Punkte leicht nachvollziehen.
2.4. Effektivierung der Totalen Probiermethode
Betrachten wir zunächst die Möglichkeiten, die sich aus der
Abweichung der mit APV erzeugten Permutationen oder Anordnungen
von der Gleichverteilung ergeben, um die TPM effektiver zu ge-
stalten. Die Grundidee dieser Methode besteht darin, alle
möglichen Ergebnispermutationen nach ihren Wahrscheinlichkeiten
zu ordnen und sie in dieser Reihenfolge durchzuprobieren.
Bei gleichverteilten zufälligen Permutationen wird durch TPM
nach Überprüfung von n! Permutationen die richtige Permutation
mit Wkt. ½ ermittelt. Bei Kenntnis von P und der Ausgangsper-
mutation X0 bzw. Xi lassen sich die Wkt. für die Erzeugung aller
n! Permutationen berechnen (siehe Teil I).
Seien P1 = p1 ≥ p2 ≥ … ≥ pn! = P2 (2)
(P1, P2 siehe Bl. 44) die geordneten Wkt. der Erzeugung
der n! möglichen Permutationen.
Sei x-Mindestanzahl von Permutationen, die überprüft werden
muß, um mit Wkt. ½ die richtige Permutation zu finden:

Aus (1) folgt, daß
Folgende Tabelle enthält für verschiedene p und n = 10; 26
die Werte für  (p1 entspr. Bl. 45)
(p1 entspr. Bl. 45)
| p |  für n = 10 (ν = 15) für n = 10 (ν = 15) |  für n = 26 (ν = 15) für n = 26 (ν = 15) |
| 0,5 | 1,81 · 106 | 2,01 · 1026 |
| 0,495 | 1,43 · 106 | 7,77 · 1025 |
| 0,49 | 1,13 · 106 | 3,04 · 1025 |
| 0,45 | 1,89 · 105 | 2,38 · 1022 |
zum Vergleich: 10!/2 = 1,81 · 106 26!/2 = 2,01 · 1026
Diese Methode der Effektivierung, der TPM setzt die Berechnung
der Wahrscheinlichkeiten und ihre Ordnung (1) voraus. Jedoch
sind allein für die Sortierung der Wahrscheinlichkeiten größen-
ordnungsmäßig n! Operationen notwendig.
(Nach /11, S. 112/ benötigt jeder beliebige Algorithmus zur
Sortierung mittels Vergleichen im Mittel nicht weniger als
c · n! · log2(n!), c > 0, Vergleiche)
Damit ist eine Effektivierung der TPM mit dieser Methode
(zumindest in Größenordnungen) für praktisch interessierende
p und n ≥ 10 praktisch nicht möglich.
Da (1) immer auf eine konkrete Ausgangspermutation bezogen ist,
kommt bei Verwendung der Variante 2 noch dazu, daß (1) für jede
Ausgangspermutation neu zu berechnen wäre.
2.5. Untermenge wahrscheinlichster Permutationen
Auch bei optimistischsten Annahmen zur EDV-Entwicklung kann
davon ausgegangen werden, daß TPM zur Überprüfung von Permu-
tationen für n ≥ 26 nicht anwendbar ist.
Nehmen wir an, der Gegner ist in der Lage, 1012 Permutationen
pro Sekunde durchzuprobieren.
(Zum Vergleich: Die Rechengeschwindigkeit des Supercomputers
CRAY X-MP wird mit 6,3 · 108 Operationen/sek angegeben.)
Für n = 26 würde der Gegner selbst unter den Bedingungen der
effektivierten TPM mit m = 0,45 (vgl. 2.4.) mehr als 750 Jahre
brauchen, um mit Wahrscheinlichkeit ½ die richtige
Permutation zu ermitteln.
Untersuchen wir deshalb die Möglichkeiten des Gegners, aus
der Menge der (für große n mit TPM nicht Überprüfbaren) Permu-
tationen eine Untermenge R der wahrscheinlichsten Permutationen
für gegebenes p und gegebene Ausgangspermutation zu bestimmen,
wobei |R| so gewählt wird, daß R vollständig überprüft werden
kann.
Sei |R| = 1018, d. h. seien 1018 Permutationen praktisch über-
prüfbar.
(Unter der Annahme, daß 1012 Permutationen/sek überprüfbar
sind, benötigt man zur Überprüfung von R 12 Tage)
Betrachten die Wkt. dafür, daß die gesuchte Permutation X
Element der Untermenge der wahrscheinlichsten Permutationen R
ist:
P(X ∈ R) ≤ |R| · P1 P1 - Wkt. der wahrscheinlichsten
Permutation (vgl. Bl. 44)
Numerische Werte für 1018 · P1:
| n | p = 0,49 | p = 0,45 |
|---|
| 26 | 1,64 · 10-8 | 2,1 · 10-5 |
| 32 | 4,64 · 10-17 | 5,99 · 10-13 |
| 45 | 4,9 · 10-37 | 1,26 · 10-30 |
| (P1 für η = 15 entspr. Bl. 45 |
Diese Tabelle zeigt, daß trotz des angesetzten hohen Aufwandes
(|R| = 1018) die Wahrscheinlichkeit äußerst gering ist, daß
sich die gesuchte Permutation unter den überprüfbaren befindet.
Hinzu kommt, daß für eine effektive Auswahl der Klasse R auch
die Wahrscheinlichkeiten der möglichen Permutationen berechnet
und geordnet werden müßten und bei Verwendung der Variante 2
die Klasse R für jede Ausgangspermutation neu zu bestimmen ist.
2.6. Rekonstruierbarkeit einzelner Stellen der Permutation
Für APV ist charakteristisch, daß sich spezielle Angriffsmög-
lichkeiten auf einzelne Stellen der Permutationen ergeben.
So ist beispielsweise offensichtlich, daß für gerades n die
Wahrscheinlichkeit, daß an erster Stelle der Ergebnispermutation
ein Element der letzten n/2 Elemente der Ausgangspermutation steht,
gleich p ist,

Daraus folgt, daß für deutlich von ½ abweichende p auch deut-
lich bevorzugt ein Element aus

an erster Stelle der Ergebnispermutation steht.
Für ungerades n gilt ein ähnlicher, jedoch komplizierter zu
formulierender Sachverhalt.
Die Tabelle der Abweichungen von π1,j (vgl. EDV-Ausdruck, Bl. 70)
zeigt, daß für die erste Stelle der Ergebnispermutation Möglich-
keiten bestehen können, die Ungleichmäßigkeit in der Verteilung
zu nutzen.
Da gilt

kann man aus der ausgedruckten Tabelle schlußfolgern, daß die
Ungleichmäßigkeit der Verteilung von der ersten zur letzten
Stelle monoton fallend ist.
Diese hier angeführten charakteristischen Besonderheiten des
APV bieten jedoch nur dann Vorteile gegenüber den bereits er-
wähnten Methoden, wenn der Gegner in der Lage ist, stellenweise
die Permutation zu überprüfen (z. B. bei Sprechtafeln). Da sich
unter dieser Bedingung jedoch die TPM auch so vereinfacht, daß
anstelle von n! nur noch maximal n/2 (n+1) Versuche zur voll-
ständigen Überprüfung notwendig sind, sind die sich aus den
Eigenschaften des APV ergebende, Effektivierungsmöglichkeiten
nicht wesentlich (vgl. Ausdruck Bl. 70)
Weiterhin ist zu beachten, daß bei Anwendung von Variante 2 die
Häufigkeitsverteilung an den einzelnen Stellen immer von der
konkreten Ausgangspermutation abhängt.
| N = 10 | P1 * N! | P2 * N! | C |
| 0,5 | 1,00006 | 0,999756 | 1,00031 |
| 0,499 | 1,00741 | 0,992442 | 1,01508 |
| 0,495 | 1,03718 | 0,96355 | 1,07642 |
| 0,49 | 1,07522 | 0,928242 | 1,15834 |
| 0,45 | 1,41348 | 0,676916 | 2,08812 |
| |
| N = 26 | |
| 0,5 | 1,00055 | 0,999756 | 1,00079 |
| 0,499 | 1,01072 | 0,989671 | 1,02127 |
| 0,495 | 1,05221 | 0,950128 | 1,10744 |
| 0,49 | 1,10593 | 0,902452 | 1,22547 |
| 0,45 | 1,61683 | 0,584962 | 2,76399 |
| |
| N = 32 | |
| 0,5 | 1,00098 | 1 | 1,00098 |
| 0,499 | 1,01104 | 0,99004 | 1,02121 |
| 0,495 | 1,05212 | 0,95099 | 1,10634 |
| 0,49 | 1,10534 | 0,903921 | 1,22283 |
| 0,45 | 1,61385 | 0,59049 | 2,73307 |
| |
| N = 45 | |
| 0,5 | 1,00113 | 0,999756 | 1,00137 |
| 0,499 | 1,01293 | 0,988078 | 1,02515 |
| 0,495 | 1,06127 | 0,942461 | 1,12606 |
| 0,49 | 1,12429 | 0,887848 | 1,26631 |
| 0,45 | 1,74454 | 0,536532 | 3,25152 |
| |
| N = 50 | |
| 0,5 | 1,00098 | 0,999451 | 1,00153 |
| 0,499 | 1,0131 | 0,987459 | 1,02596 |
| 0,495 | 1,06279 | 0,940667 | 1,12983 |
| 0,49 | 1,1277 | 0,884756 | 1,27459 |
| 0,45 | 1,77321 | 0,528345 | 3,35616 |
| |
| N = 100 | |
| 0,5 | 1,00098 | 0,997925 | 1,00306 |
| 0,499 | 1,01512 | 0,983976 | 1,03165 |
| 0,495 | 1,07342 | 0,929825 | 1,15443 |
| 0,49 | 1,15026 | 0,865712 | 1,32868 |
| 0,45 | 1,95053 | 0,474739 | 4,10864 |
| |
| P1 = max π1,j |
| P2 = min π1,j |
| C = P1/P2 |
| ν = 15 |
3. Anwendungsbedingungen
3.1. Anforderungen an die Zufallsfolge
Die Zufallsfolge zur Bildung der Zahlenfolge (δi)i vgl.
Realisierung des APV auf EDVA (Bl. 12), hat entscheidenden
Einfluß auf die Qualität der erzeugten Permutationen/Anord-
nungen.
So wurde bei allen Untersuchungen vorausgesetzt, daß es sich
bei der Zufallsfolge um unabhängige Realisierungen einer DZG
handelt. In den Teilen I und II wurde gezeigt, welchen Ein-
fluß p (Wkt. für Auftreten von 1 in der Zufallsfolge) auf die
Abweichung vom idealen Zufall hat.
Deshalb muß die Zufallsfolge als Ausgangsfolge eines physika-
lischen Zufallsgenerators folgenden Bedingungen genügen:
Anwendungsbedingung (AB) 1
Der verwendete Zufallsgenerator muß Folgen von
hinreichend unabhängigen Realisierungen einer auf {0,1}
hinreichend gleichverteilten DZG, d. h. |p - ½| ≤ ε mit ε « ½
erzeugen.
AB 1 ist zu gewährleisten durch
· das Konstruktionsprinzip des Zufallsgenerators und
· regelmäßige Überprüfung des. Zufallsgenerators.
Die Zufallsgeneratoren T 106, T 107 und T 113 gewährleisten
durch ihr Konstruktionsprinzip in Verbindung mit einer regel-
mäßigen Überprüfung, z. B. monatlich mit dem Programm PA 04,
die Erfüllung von AB 1.
AB 1 beinhaltet globale Eigenschaften des verwendeten Zufalls-
generators.
In Ergänzung dazu beinhaltet die folgende AB 2 die Forderung
nach einer kontinuierlichen Überprüfung der gesamten verwen-
deten Zufallsfolge:
AB 2
Die gesamte Zufallsfolge ist in relativ kurzen Abschnitten
(Länge ≥ 1000 Bit) mit einfachen Kriterien auf Abweichungen
von der Gleichverteilung sowie auf Abhängigkeit zu kontrollieren.
Bei der gegenwärtigen Technologie der Chiffriermittelproduk-
tion mit APV auf der EDVA PRS 4000 /12/ wird AB 2 durch
folgende Tests gewährleistet:
· Abschnittslänge 100 Worte = 1600 Bit, d. h. L = 1600
· Kriterien: h1 - Anzahl von 1 im Abschnitt
h2 - Anzahl der Bitwechsel im Abschnitt
("3δ"-Regel" für Anzahl Bit und Bitwechsel)
Für L = 1600 gewährleistet dieses Kriterium, daß
|p - ½| < 0,04
3.2. Wahl des Parameters ν
Bei der Realisierung des APV auf EDVA ist der Parameter ν
zur Bildung der Zahlenfolge (νi)i festzulegen (vgl. Bl. 12).
Die Wahl des Parameters ν hat, wie im Teil I gezeigt wird,
Einfluß auf die Abweichung der erzeugten Permutationen/Anord-
nungen vom "idealen Zufall" (vgl. z. B. Bl. 45 - 47).
Gleichzeitig zeigt sich auch, daß die Wahl von ν nicht unab-
hängig von n erfolgen kann.
Da der Grad der Abweichung vom "idealen Zufall" noch einen
relativ breiten Spielraum für die Wahl von ν läßt, sind bei
der Wahl folgende, für die praktische Realisierung auf EDVA
wichtige Kriterien zu beachten:
- ν ist so zu wählen, daß APV rechentechnisch günstig zu reali-
sieren ist. Insbesondere ist die Wahl von ν mit der Verar-
beitungsbreite der konkreten EDVA zu vereinbaren:
PRS 4000 - wortweise Verarbeitung, 1 Wort = 16 Bit (davon
1 Vorzeichenbit)
μR auf Z 80-Basis - byteweise Verarbeitung
- der Zusammenhang von ν und n sollte möglichst so sein, daß
für eine möglichst breite Klasse von h eine stabile und
möglichst effektive Lösung für die Mittelproduktion erar-
beitet werden kann
Ausgehend von den Erfahrungen bei der Realisierung des APV
auf den PRS 4000 wird gefordert:
AB 3:
Für die Wahl des Approximationsparameters ν für die
Realisierung des APV auf EDVA gilt:
∀ n ∈ 2,45 : ν ≥ 45,
∀ n ∈ 46,10000 : ν ≥ 30.
Begründungen:
1. Mit ν ≥ 15 für n ≤ 45 wird eine einheitliche Lösung für
alle Chiffriermittel auf der Basis der üblichen Misch-
alphabete möglich (Ziffern-, Buchstaben-, Buchstaben-/Ziffern-
Mischalphabete einschließlich kyrillischem Alphabet)
2. Die Ergebnisse der Teile I, II sowie des Punktes III. 2 recht-
fertigen die Festlegungen der AB 3. Mit wachsenden _______
werden. die Eigenschaften des APV verbessert, deshalb ist
Festlegung ν ≥ 15 bzw. ν ≥ 30 gerechtfertigt.
3. Für n > 10000 ist konkret zu entscheiden, ob APV anzuwenden ist.
4. Mit den Angaben ν ≥ 15 bzw. ν ≥ 30 wird die Möglichkeit der
Anpassung an die Verarbeitungsbreite gewährleistet, für die
Realisierung auf PRS 4000 wurde festgelegt:
∀ n ≤ 45 ν = 15
∀ n > 45 ν = 31
3.3. Erzeugung von Folgen von Permutationen und Anordnungen
Wie bereits in der Einleitung vermerkt, kann als typisch ange-
nommen werden, daß Einheiten aus h Permutationen/Anordnungen
erzeugt werden.
Für die Erzeugung von Folgen von Permutationen gilt folgende
AB 4:
Für die Erzeugung einer Folge von Permutationen 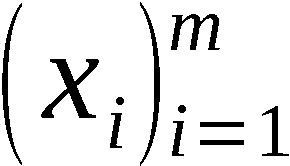 ist
die im Pkt. II.3.1. beschriebene Variante 2 anzuwenden, d. h.
∀ i ∈ 1,m : Xi = PVn (Xi-1)
wobei X0-beliebige Ausgangspermutation.
Aufgrund der Eigenschaften der Variante 2 (asymptotische Gleich-
verteilung für m → ∞) ist eine technologische Lösung anzustreben,
die nur bei Programmstart mit X0 beginnt, d. h., m ist mög-
lichst groß zu wählen. Für die Wahl von X0 gibt es keine Ein-
schränkungen, z, B. ist die "natürliche" Permutation (1,2, … ,n)
möglich.
Für die Erzeugung von Folgen von Anordnungen gilt analog die
folgende
AB 5
Für die Erzeugung einer Folge von k-Anordnungen
ist
die im Pkt. II.3.1. beschriebene Variante 2 anzuwenden, d. h.
∀ i ∈ 1,m : Xi = PVn (Xi-1)
wobei X0-beliebige Ausgangspermutation.
Aufgrund der Eigenschaften der Variante 2 (asymptotische Gleich-
verteilung für m → ∞) ist eine technologische Lösung anzustreben,
die nur bei Programmstart mit X0 beginnt, d. h., m ist mög-
lichst groß zu wählen. Für die Wahl von X0 gibt es keine Ein-
schränkungen, z, B. ist die "natürliche" Permutation (1,2, … ,n)
möglich.
Für die Erzeugung von Folgen von Anordnungen gilt analog die
folgende
AB 5
Für die Erzeugung einer Folge von k-Anordnungen  ist
die im Pkt. II.3.2. beschriebene Variante 2 anzuwenden, d.h.
ist
die im Pkt. II.3.2. beschriebene Variante 2 anzuwenden, d.h.

wobei Yi-1 - die im (i-1)ten Schritt faktisch entstandene Er-
gebnispermutation (durch k Vertauschungen aus
Yi-2 entstanden gemäß 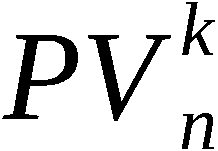 )
Y0 - beliebige Ausgangspermutation von Grad n
Bezüglich Y0 gelten hier die gleichen Bemerkungen wie zu X0
nach AB 4.
3.4. Kryptologische und programmtechnische Kontrollen
(1) Aus kryptologischen Erwägungen, die mehr psychologisch als
mathematisch begründet sind, wird gefordert, daß bei Chif-
friermitteln auf der Basis von zufälligen Permutationen/An-
ordnungen innerhalb einer Schlüsselserie (Einheit) aufein-
anderfolgende Permutationen/Anordnungen hinreichend unter-
schiedlich voneinander sind.
Deshalb ist die Anzahl von Übereinstimmungen (Fixpunkten)
aufeinanderfolgender Permutationen einzuschränken, für An-
ordnungen ist diese Einschränkung sinnvoll für die fakti-
schen Ergebnispermutationen.
Für die Erzeugung von Folgen von Permutationen gilt deshalb
folgende
AB 6
Sei s - Anzahl der maximal zulässigen Fixpunkte aufeinander-
folgender Permutationen Xi und Xi+1 (Ergebnispermu-
tationen Yi und Yi+1)
Dann ist
∀ n ≥ 10 s = 6 zu gewährleisten.
Für n < 10 und für Anordnungen muß diese Festlegung in Ab-
hängigkeit von n und k sowie der Verwendung jeweils konkret
getroffen werden.
Begründung:
1. s = 6 gewährleistet einerseits die Forderung (für die an-
gegebenen n), daß sich aufeinanderfolgende Permutationen
hinreichend unterscheiden.
2. Gleichzeitig gewährleistet s = 6, daß durch diese Fest-
legung keine unzulässig große Einschränkung der Zufällig-
keit entsteht.
Es gilt: ns - Anzahl Fixpunkte
P (ns > 6) ≈ 8 · 10-5
(Für zufällige Permutationen vom Grad n gilt
)
Y0 - beliebige Ausgangspermutation von Grad n
Bezüglich Y0 gelten hier die gleichen Bemerkungen wie zu X0
nach AB 4.
3.4. Kryptologische und programmtechnische Kontrollen
(1) Aus kryptologischen Erwägungen, die mehr psychologisch als
mathematisch begründet sind, wird gefordert, daß bei Chif-
friermitteln auf der Basis von zufälligen Permutationen/An-
ordnungen innerhalb einer Schlüsselserie (Einheit) aufein-
anderfolgende Permutationen/Anordnungen hinreichend unter-
schiedlich voneinander sind.
Deshalb ist die Anzahl von Übereinstimmungen (Fixpunkten)
aufeinanderfolgender Permutationen einzuschränken, für An-
ordnungen ist diese Einschränkung sinnvoll für die fakti-
schen Ergebnispermutationen.
Für die Erzeugung von Folgen von Permutationen gilt deshalb
folgende
AB 6
Sei s - Anzahl der maximal zulässigen Fixpunkte aufeinander-
folgender Permutationen Xi und Xi+1 (Ergebnispermu-
tationen Yi und Yi+1)
Dann ist
∀ n ≥ 10 s = 6 zu gewährleisten.
Für n < 10 und für Anordnungen muß diese Festlegung in Ab-
hängigkeit von n und k sowie der Verwendung jeweils konkret
getroffen werden.
Begründung:
1. s = 6 gewährleistet einerseits die Forderung (für die an-
gegebenen n), daß sich aufeinanderfolgende Permutationen
hinreichend unterscheiden.
2. Gleichzeitig gewährleistet s = 6, daß durch diese Fest-
legung keine unzulässig große Einschränkung der Zufällig-
keit entsteht.
Es gilt: ns - Anzahl Fixpunkte
P (ns > 6) ≈ 8 · 10-5
(Für zufällige Permutationen vom Grad n gilt

(vgl. /10/, S. 72 f.)
Asymptotisch gilt (für n → ∞)

Numerische Werte:
| n = 10 | n = 26 | n → ∞ |
| P(ns > 6) | 7,8 10-5 | 8,3 10-5 | 8,3 10-5 |
Die Werte zeigen, daß praktisch für alle n ≥ 10 mit asympto-
tischer Näherung gearbeitet werden kann.
3. Mit der Festlegung S = 6 für n ≥ 10 wird die Mehrzahl
der Typen von Chiffriermitteln erfaßt.
(2) Aufgrund der Eigenschaften von APV, speziell auch der un-
tersuchten Angriffsmöglichkeiten des Gegners, kann bei
Einhaltung der bisher formulierten Bedingungen auf weitere
statistische Tests der erzeugten Permutationen/Anordnungen
im Prozeß der Chiffriermittelproduktion verzichtet werden.
Das schließt nicht aus, daß aus mittelspezifischen Überle-
gungen (kryptologische Anforderungen aus der Anwendung der
Mittel) zusätzliche, auch statistische, Tests der erzeug-
ten Permutationen/Anordnungen erforderlich sein können.
(3) AB 7
Durch geeignete Maßnahmen (programmtechnische und technolo-
gische) ist zu gewährleisten, daß APV exakt realisiert wird,
die genannten Anwendungsbedingungen eingehalten werden und
Abarbeitungsfehler ausgeschlossen sind.
4. Zusammenfassung
Die in diesem Dokument fixierten Untersuchungsergebnisse zum
Algorithmus Paarweises Vertauschen führen zu folgender Schluß-
folgerung:
Zur Produktion von Chiffriermitteln auf der Basis von zu-
fälligen Permutationen/Anordnungen mittels Rechentechnik
in der Abteilung XI sollte für die Erzeugung der Permu-
tationen/Anordnungen in der Regel APV genutzt werden. Dabei
sind die Anwendungsbedingungen gemäß III.3 exakt und voll-
ständig einzuhalten.
Sonderfälle (z. B. n > 10000 oder k « n) sollten mit der
für kryptologische Fragen zuständigen Struktureinheit der
Abteilung XI abgestimmt werden.
Begründung:
(1) Der Algorithmus APV ist kryptologisch qualitätsgerecht;
es wird eine irreguläre Folge von Permutationen/Anordnungen
erzeugt, wenn die AB gemäß III.3 eingehalten werden.
Es sind zum Teil auch andere AB denkbar. Da es nicht mög-
lich ist, alle zukünftigen Entwicklungen vorherzusehen, sind
nicht alle Möglichkeiten untersucht worden. Modifizierungen
der AB bei zukünftigen Entwicklungen werden deshalb nicht
absolut ausgeschlossen.
(2) Der Algorithmus APV ist rechnerfreundlich in seiner
Realisierung als Unterprogramm. Er ist auf beliebiger
Rechentechnik realisierbar (einschließlich Mikrorechen-
technik) und deshalb unabhängig von seiner derzeitigen
Realisierung auf PRS 4000 auch in der Perspektive
einsetzbar.
(3) Der Algorithmus APV ist der in der Abteilung XI am besten
analysierte Algorithmus zur Erzeugung zufälliger Permuta-
tionen/Anordnungen. Die gegenwärtig auf der EDVA PRS 4000
der Abteilung XI realisierte Technologie der Produktion
von Chiffriermitteln auf der Basis zufälliger Permutationen/
Anordnungen, die auf Realisierungen des APV in den Unter-
programmen M896 bzw. M897 (für n > 45) aufbauend /12/,
realisiert die Anwendungsbedingungen gemäß III.3.
















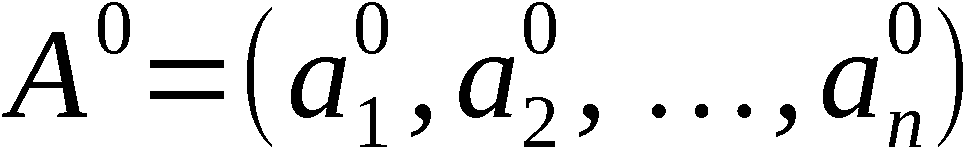


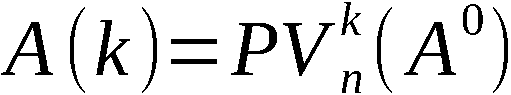
 eine Folge unabhängiger Realisierungen einer auf
(0,1) gleichverteilten (stetigen) Zufallsgröße X ist, dann sind bei
beliebiger Ausgangspermutation (a
eine Folge unabhängiger Realisierungen einer auf
(0,1) gleichverteilten (stetigen) Zufallsgröße X ist, dann sind bei
beliebiger Ausgangspermutation (a die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige Permutation
die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige Permutation 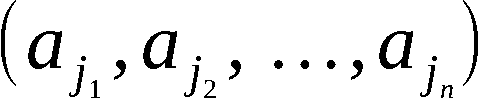 zu erhalten.
Es gilt
zu erhalten.
Es gilt
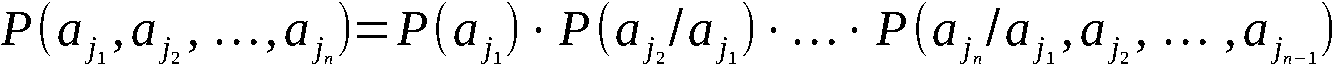
 -Wahrscheinlichkeit dafür, daß an
r-ter Stelle das Element
-Wahrscheinlichkeit dafür, daß an
r-ter Stelle das Element 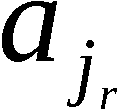 , erscheint unter der Bedingung, daß
, erscheint unter der Bedingung, daß
 an den Stellen 1, 2, … , r-1 stehen (r ∈
an den Stellen 1, 2, … , r-1 stehen (r ∈ 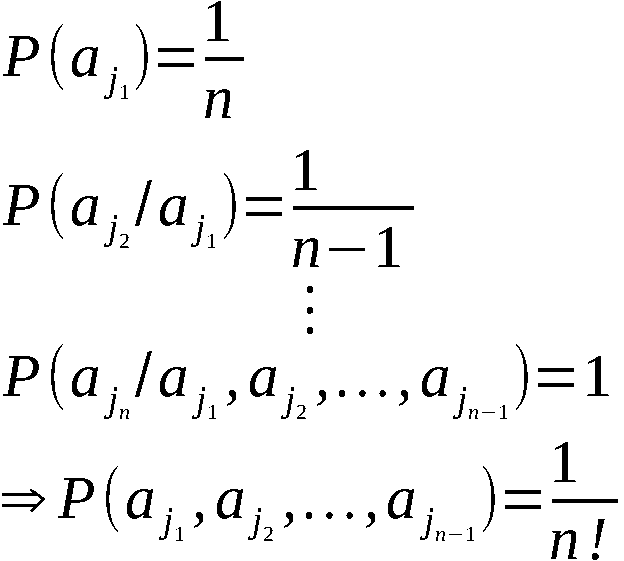
 eine Folge unabhän-
giger Realisierungen einer auf (0,1) gleichverteilten Zufallsgröße
ist, dann sind bei beliebiger Ausgangspermutation alle k-Anordnun-
gen gleichwahrscheinlich.
Beweis:
Sei
eine Folge unabhän-
giger Realisierungen einer auf (0,1) gleichverteilten Zufallsgröße
ist, dann sind bei beliebiger Ausgangspermutation alle k-Anordnun-
gen gleichwahrscheinlich.
Beweis:
Sei 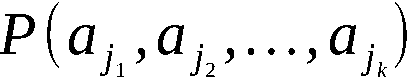 die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige k-Anordnung
die Wahrscheinlichkeit dafür, im Ergebnis
der Anwendung von APV eine beliebige k-Anordnung  zu erhalten.
Es gilt
zu erhalten.
Es gilt

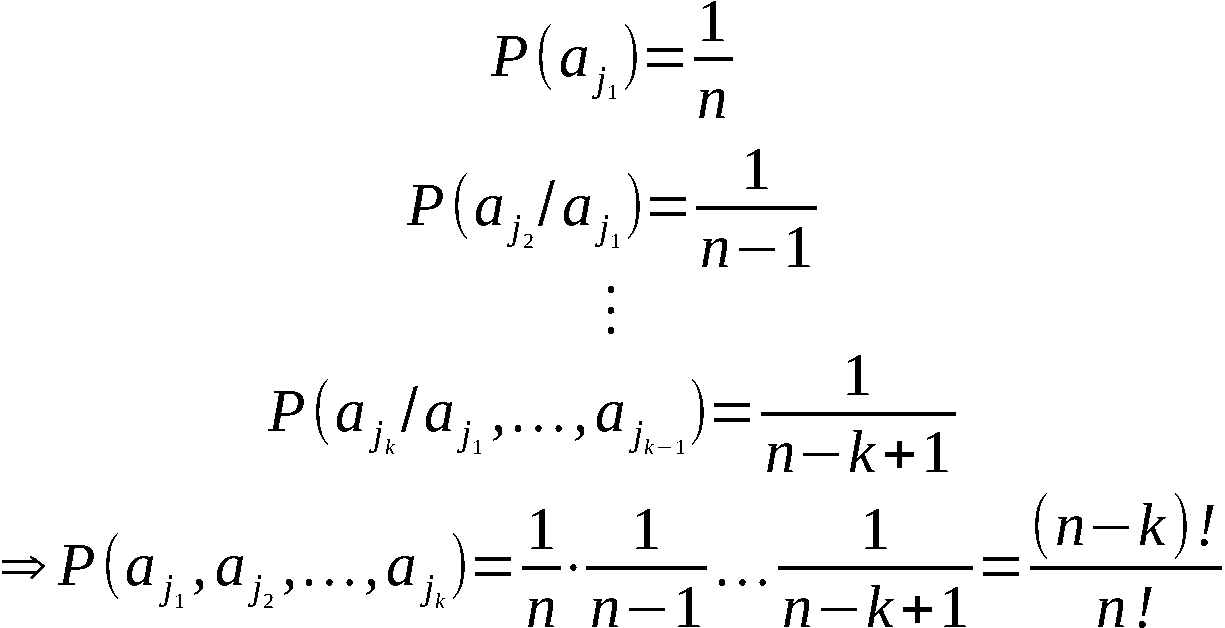
 möglichen k-An-
ordnungen ist, sind damit alle Anordnungen gleichwahrscheinlich.
Bei der Entscheidung, APV als grundsätzliche Erzeugungsvorschrift
für die Herstellung von zufälligen Permutationen und Anordnungen
anzuwenden, wurden u. a. folgende Charakteristika von APV berück-
sichtigt:
(1) APV erfaßt Permutationen und Anordnungen und ist für alle prak-
tisch notwendigen Grade n der Permutationen auf PRS 4000 zu
realisieren.
(2) Die Anzahl der notwendigen Schritte hängt nur von n bzw. k ab
und ist unabhängig von der Wahl von A
möglichen k-An-
ordnungen ist, sind damit alle Anordnungen gleichwahrscheinlich.
Bei der Entscheidung, APV als grundsätzliche Erzeugungsvorschrift
für die Herstellung von zufälligen Permutationen und Anordnungen
anzuwenden, wurden u. a. folgende Charakteristika von APV berück-
sichtigt:
(1) APV erfaßt Permutationen und Anordnungen und ist für alle prak-
tisch notwendigen Grade n der Permutationen auf PRS 4000 zu
realisieren.
(2) Die Anzahl der notwendigen Schritte hängt nur von n bzw. k ab
und ist unabhängig von der Wahl von A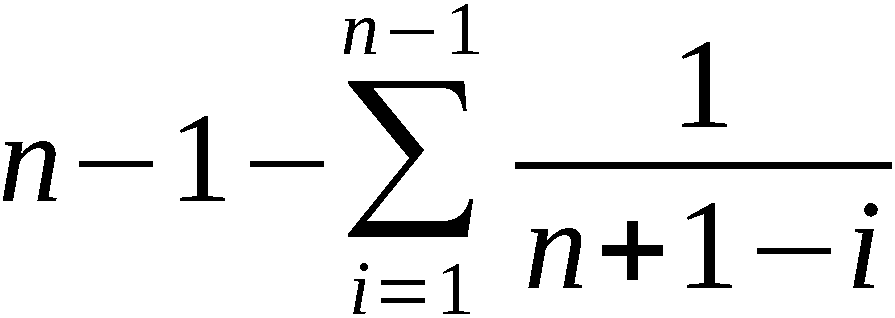 ist.
Es wird bemerkt, daß kleine Abweichungen von der Gleichverteilung in
den kleinsten signifikanten Digitalstellen der Realisierungen der auf
(0,1) gleich verteilten Zufallsgröße praktisch keinen Einfluß auf die
Verteilung der Zufallspermutationen haben.
In verallgemeinerter Form wurde der Algorithmus auch in einer sowje-
tischen Quelle beschrieben /4/. Die Verallgemeinerung besteht in der
Verwendung der Zahlenfolge
ist.
Es wird bemerkt, daß kleine Abweichungen von der Gleichverteilung in
den kleinsten signifikanten Digitalstellen der Realisierungen der auf
(0,1) gleich verteilten Zufallsgröße praktisch keinen Einfluß auf die
Verteilung der Zufallspermutationen haben.
In verallgemeinerter Form wurde der Algorithmus auch in einer sowje-
tischen Quelle beschrieben /4/. Die Verallgemeinerung besteht in der
Verwendung der Zahlenfolge

 der Ausgangspermutation, d. h.
der Ausgangspermutation, d. h.
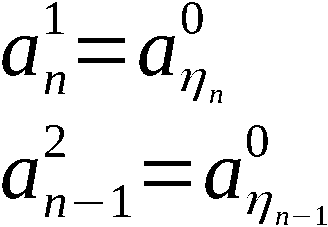

 ∀ i ∈
∀ i ∈ 

 stellen unabhängige Realisierungen einer DZG dar, die den
Wert 1 mit der Wahrscheinlichkeit p und den Wert 0 mit der
Wahrscheinlichkeit q = 1-p annimmt.
Die Annahme der Unabhängigkeit der Realisierungen wird als zu-
lässig angesehen, weil für die Chiffriermittelproduktion von der
Verwendung eines physikalischen Zufallsgenerators ausgegangen
werden kann, der den notwendigen kryptologischen Kontrollen unter-
liegt und somit die Bedingung der Unabhängigkeit aufeinanderfol-
gender binärer Elemente hinreichend gut erfüllt.
Andererseits würde ohne diese Annahme der mathematische Unter-
suchungsaufwand stark anwachsen, teilweise müßten andere, kom-
pliziertere mathematische Mittel eingesetzt werden.
Aus dem gleichen Grund wird der in der Praxis auftretende Fall
eines zeitlich schwankenden p nicht speziell untersucht.
Die Monotonieeigenschaften aller untersuchten Eigenschaften,
die von p abhängen, lassen vermuten, daß für diese Eigenschaften
im Fall eines zeitlich schwankenden p eine Abschätzung, die auf
der kryptologisch sicheren Seite liegt, angegeben werden kann,
wenn für p der Wert konstant fest gehalten wird, der am stärksten
von ½ abweicht.
Aus den Eigenschaften von Zufallsgeneratoren für die Chiffrier-
mittelproduktion folgt außerdem, daß bei Notwendigkeit auch die
vereinfachende Annahme getroffen werden kann, daß p nur gering-
fügig von ½ abweicht.
7. Juli 1982
Teil I
Erzeugung einer Permutation oder Anordnung durch APV
Inhalt:
1. Aufgabenstellung und mathematisches Modell
2. Der Spezialfall p = ½
3. Der allgemeine Fall
3.1. Mathematische Grundlagen
3.2. Theoretische Aussagen
3.3. Numerische Aussagen
3.4. Ergänzung zu Punkt 3.2. und 3.3.
4. Bistochastische Matrizen
1. Aufgabenstellung und mathematisches Modell
Im vorliegenden Teil I werden die Eigenschaften des APV bei
einmaliger Anwendung auf eine Ausgangspermutation untersucht.
Mathematische interessieren dabei
- das zufällige Ereignis {A
stellen unabhängige Realisierungen einer DZG dar, die den
Wert 1 mit der Wahrscheinlichkeit p und den Wert 0 mit der
Wahrscheinlichkeit q = 1-p annimmt.
Die Annahme der Unabhängigkeit der Realisierungen wird als zu-
lässig angesehen, weil für die Chiffriermittelproduktion von der
Verwendung eines physikalischen Zufallsgenerators ausgegangen
werden kann, der den notwendigen kryptologischen Kontrollen unter-
liegt und somit die Bedingung der Unabhängigkeit aufeinanderfol-
gender binärer Elemente hinreichend gut erfüllt.
Andererseits würde ohne diese Annahme der mathematische Unter-
suchungsaufwand stark anwachsen, teilweise müßten andere, kom-
pliziertere mathematische Mittel eingesetzt werden.
Aus dem gleichen Grund wird der in der Praxis auftretende Fall
eines zeitlich schwankenden p nicht speziell untersucht.
Die Monotonieeigenschaften aller untersuchten Eigenschaften,
die von p abhängen, lassen vermuten, daß für diese Eigenschaften
im Fall eines zeitlich schwankenden p eine Abschätzung, die auf
der kryptologisch sicheren Seite liegt, angegeben werden kann,
wenn für p der Wert konstant fest gehalten wird, der am stärksten
von ½ abweicht.
Aus den Eigenschaften von Zufallsgeneratoren für die Chiffrier-
mittelproduktion folgt außerdem, daß bei Notwendigkeit auch die
vereinfachende Annahme getroffen werden kann, daß p nur gering-
fügig von ½ abweicht.
7. Juli 1982
Teil I
Erzeugung einer Permutation oder Anordnung durch APV
Inhalt:
1. Aufgabenstellung und mathematisches Modell
2. Der Spezialfall p = ½
3. Der allgemeine Fall
3.1. Mathematische Grundlagen
3.2. Theoretische Aussagen
3.3. Numerische Aussagen
3.4. Ergänzung zu Punkt 3.2. und 3.3.
4. Bistochastische Matrizen
1. Aufgabenstellung und mathematisches Modell
Im vorliegenden Teil I werden die Eigenschaften des APV bei
einmaliger Anwendung auf eine Ausgangspermutation untersucht.
Mathematische interessieren dabei
- das zufällige Ereignis {A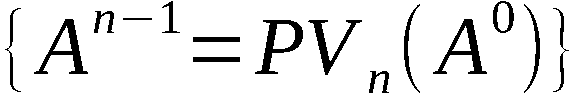 , das darin besteht,
daß bei Anwendung des APV auf A
, das darin besteht,
daß bei Anwendung des APV auf A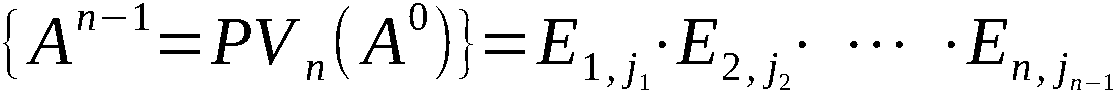
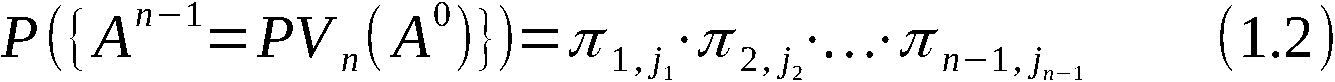

 Zur weiteren Untersuchung der Wahrscheinlichkeiten π
Zur weiteren Untersuchung der Wahrscheinlichkeiten π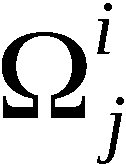 j ∈
j ∈ 
 Dann erhalten wir aus (1.1)
Dann erhalten wir aus (1.1)
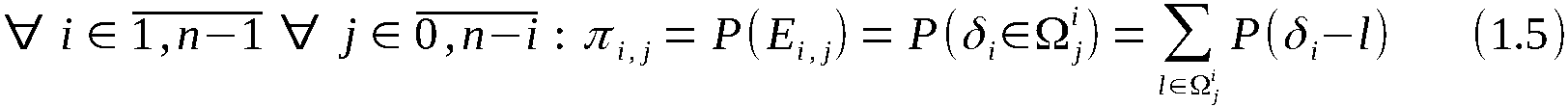
 .
Dazu benutzen wir, daß
.
Dazu benutzen wir, daß


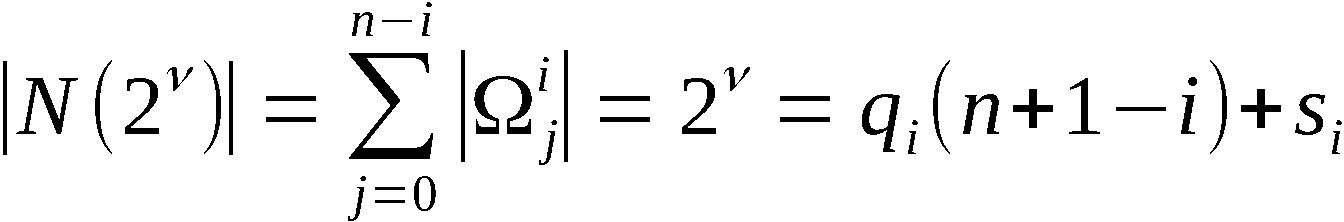
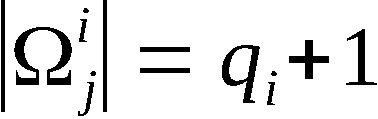 und n + 1 - s
und n + 1 - s Durch die zusätzliche Forderung
2
Durch die zusätzliche Forderung
2 .
Jedoch wird auch bei Verwendung einer
.
Jedoch wird auch bei Verwendung einer 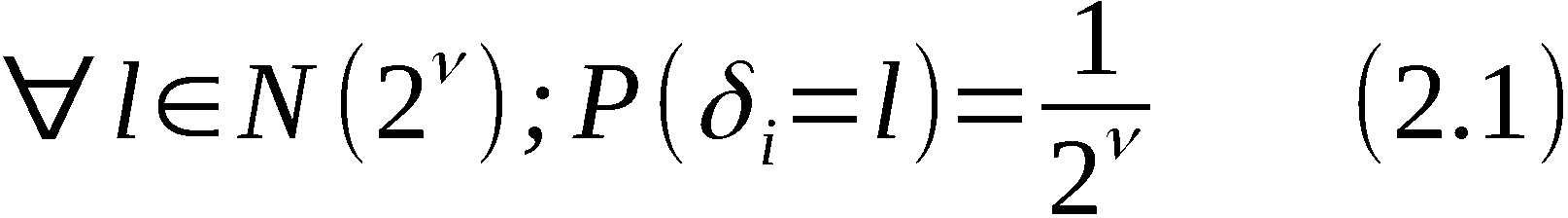
 Wir bezeichnen
(2.2)
Wir bezeichnen
(2.2)

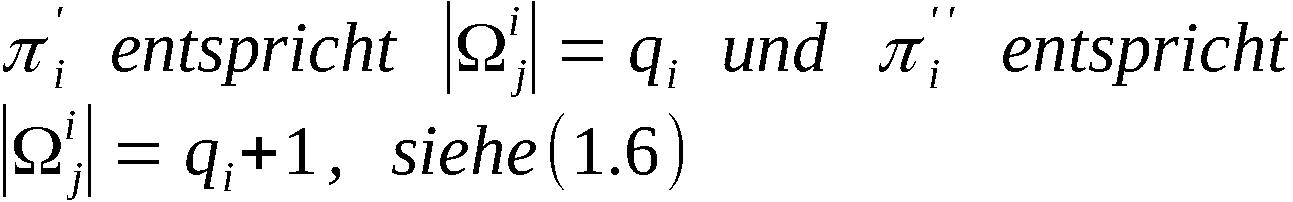

 sind immer und die Mengen
sind immer und die Mengen 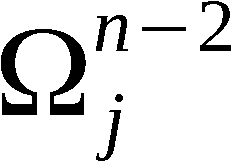 sind
nie gleichmächtig (für verschiedene j), somit kann in diesem Falle
keine Permutation A
sind
nie gleichmächtig (für verschiedene j), somit kann in diesem Falle
keine Permutation A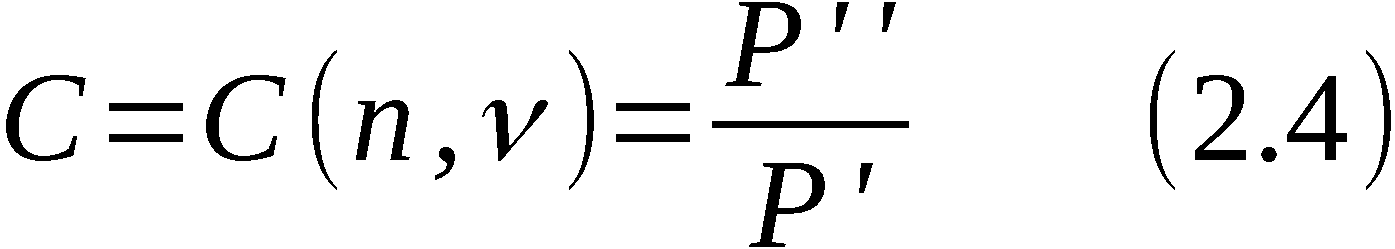







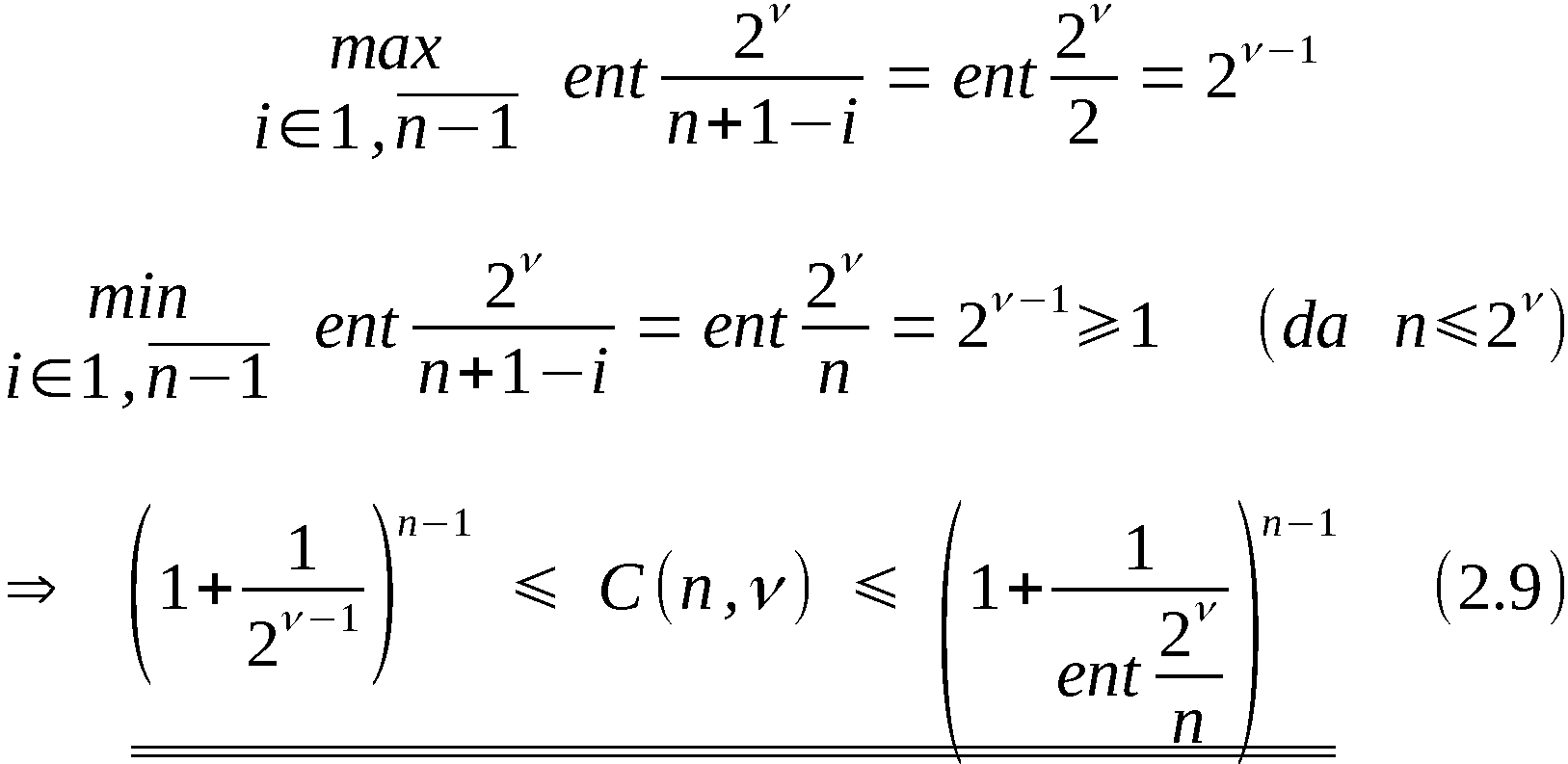
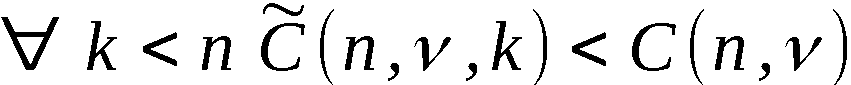 gilt, können
wir auf die Angabe genauer Wert für ͠
gilt, können
wir auf die Angabe genauer Wert für ͠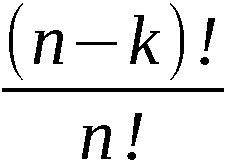 mit
fallendem k geringer wird (relativ zu
mit
fallendem k geringer wird (relativ zu 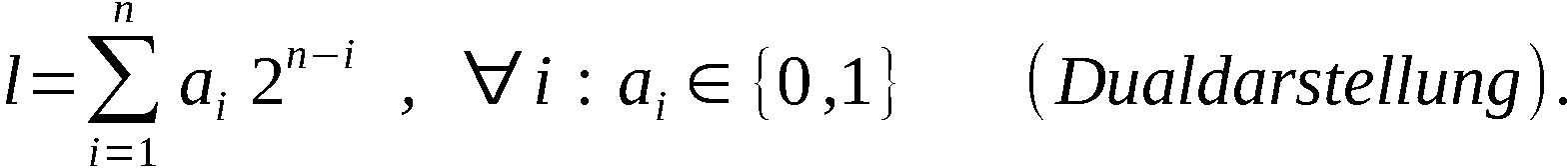
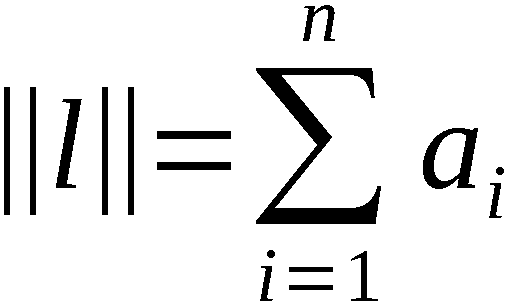 Weiterhin betrachten wir die diskrete Zufallsgröße δ auf N(2
Weiterhin betrachten wir die diskrete Zufallsgröße δ auf N(2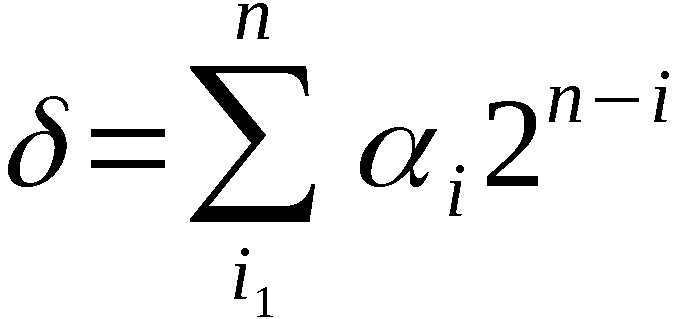
 ‖ Eine eineindeutige Abbildung λ : I → I
‖ Eine eineindeutige Abbildung λ : I → I Konstruktion einer eed Abbildung Θ von I auf I
Konstruktion einer eed Abbildung Θ von I auf I
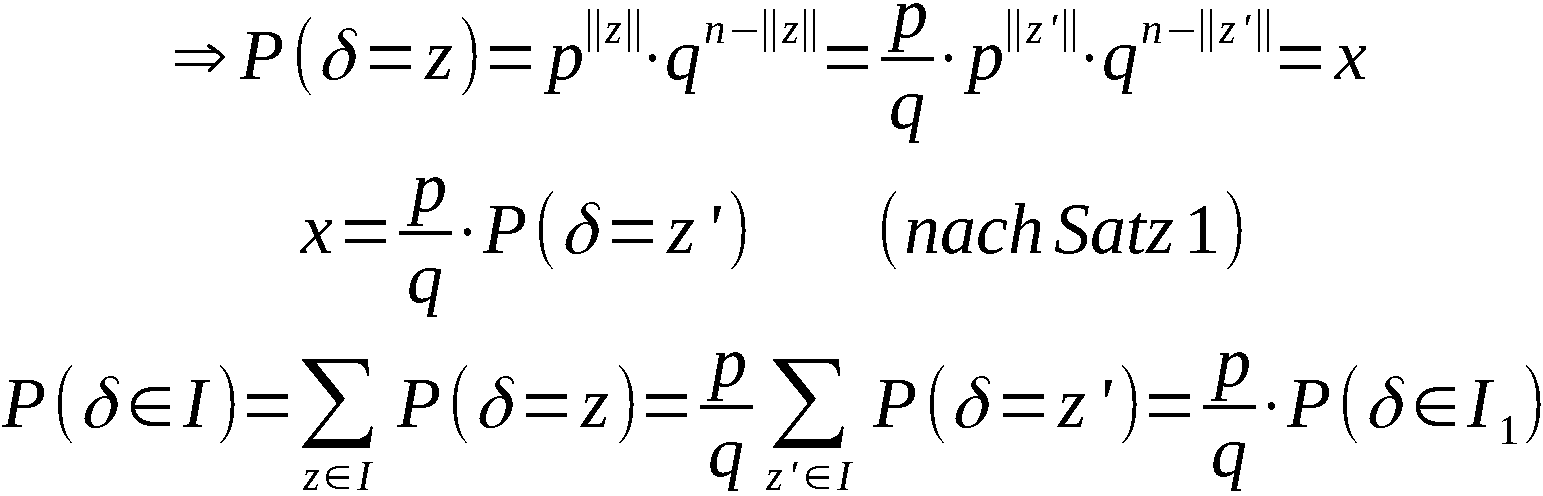

 Wir ordnen alle die j Zahlen a
Wir ordnen alle die j Zahlen a



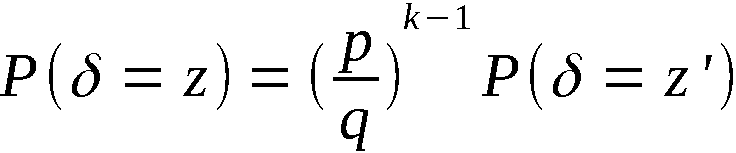
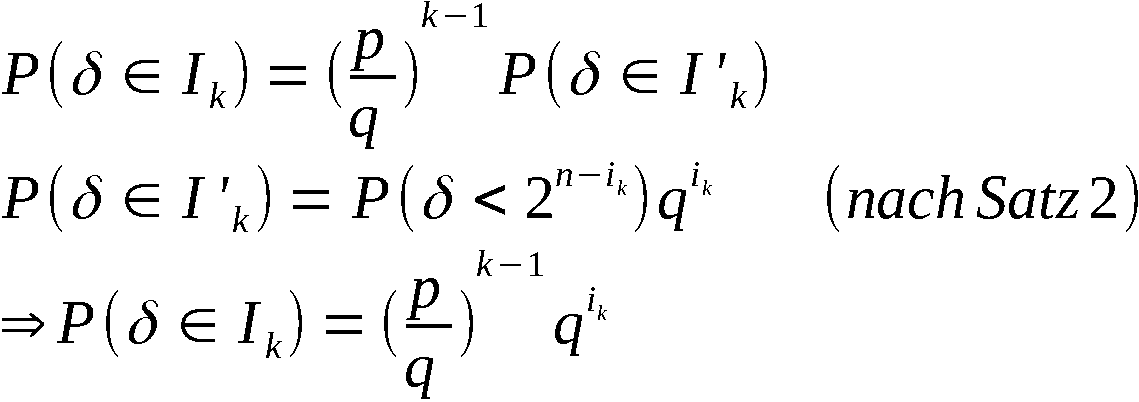




 , λ' ; I → N(2
, λ' ; I → N(2 Beweis:
Seien
Beweis:
Seien
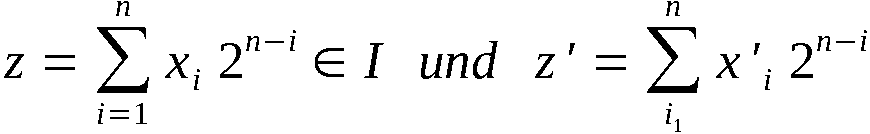




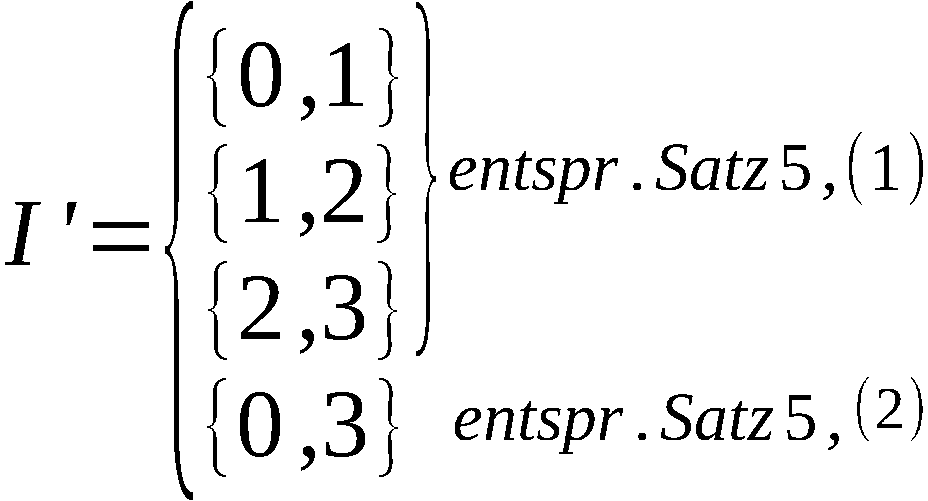
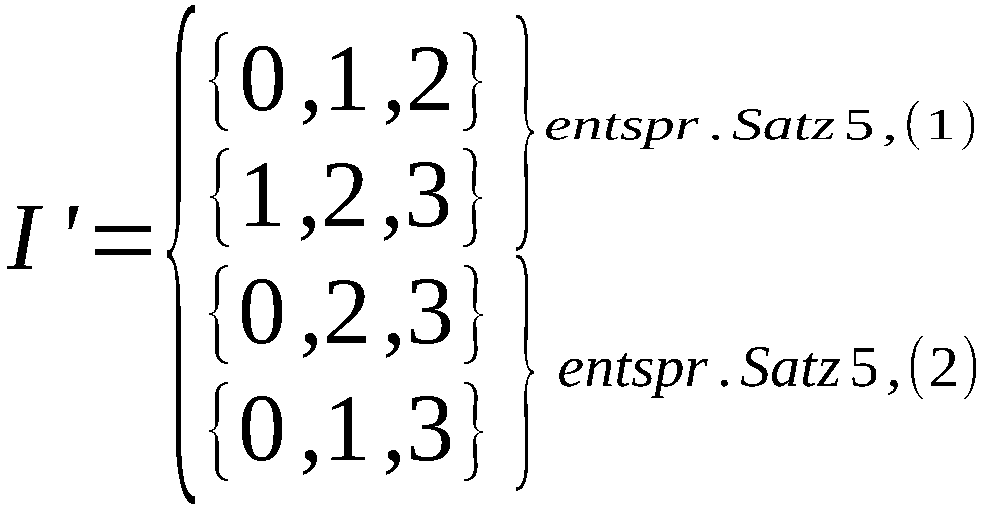
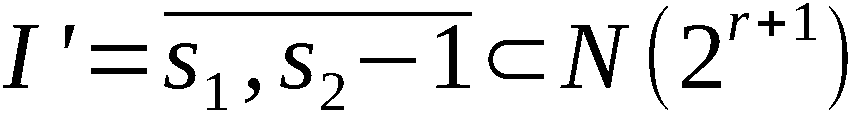 Konstruktion einer kontrahierenden Abbildung λ" von I' auf I
Konstruktion einer kontrahierenden Abbildung λ" von I' auf I
 Konstruktion einer kontrahierenden Abbildung λ" von I' auf I
Konstruktion einer kontrahierenden Abbildung λ" von I' auf I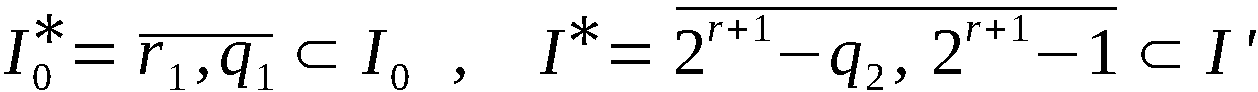


 und die Mächtigkeit von
und die Mächtigkeit von 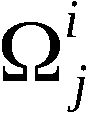 entweder
entweder 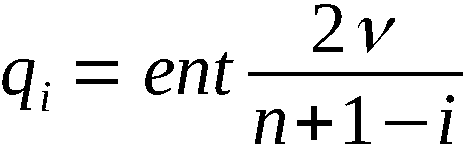 oder q
oder q lassen sich
die Werte von π'
lassen sich
die Werte von π'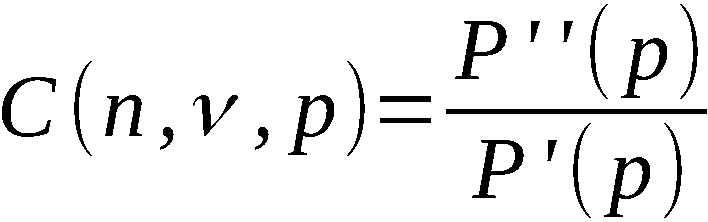

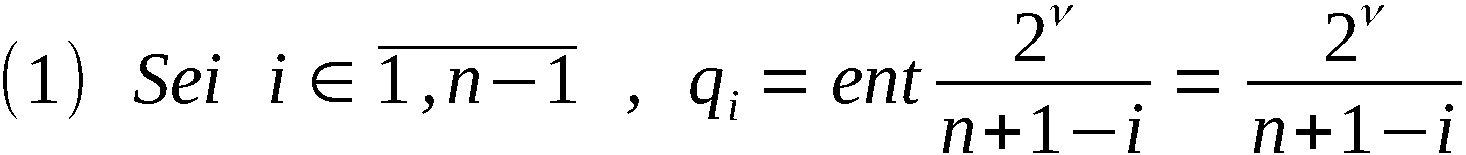
 und aus (3.7.) folgt:
π'
und aus (3.7.) folgt:
π'

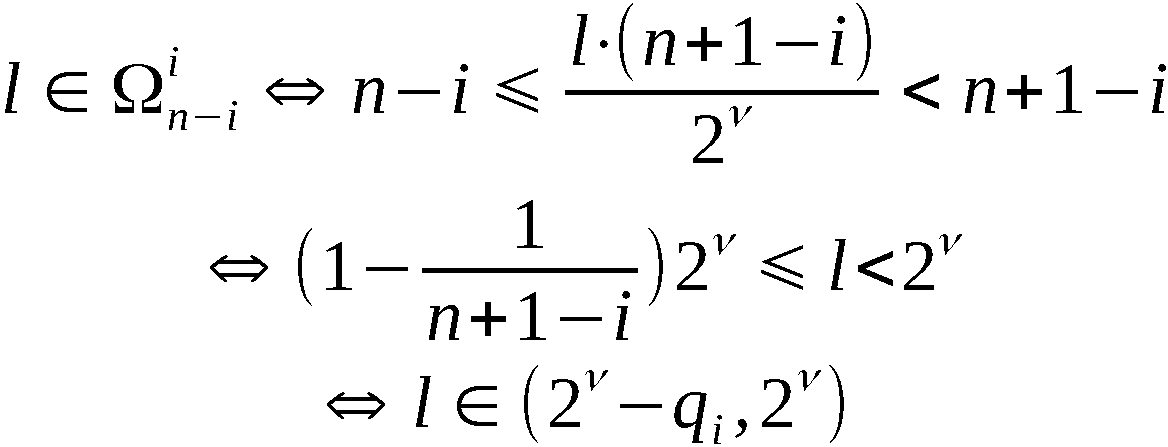
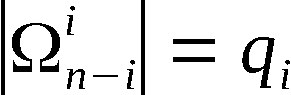 und aus (1.5.), (3.9.) und (3.11)
folgt
π
und aus (1.5.), (3.9.) und (3.11)
folgt
π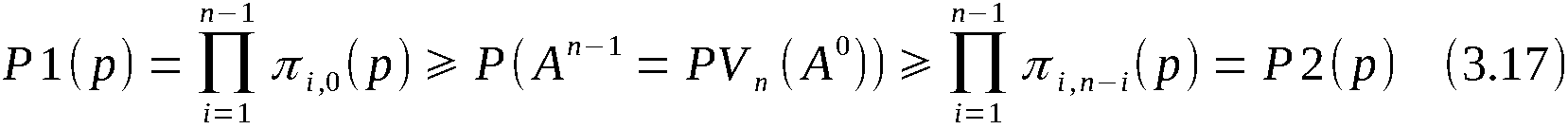

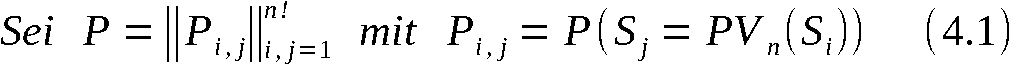
 mit A
mit A
 wobei {A
wobei {A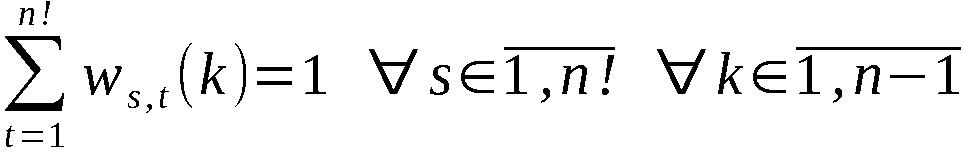
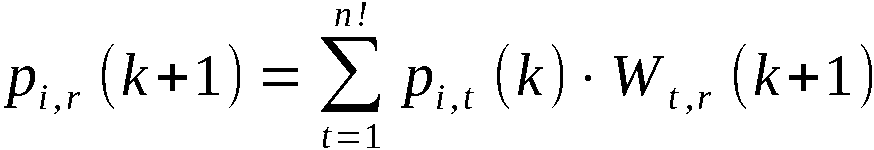 .
.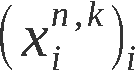 untersucht werden.
Die Untersuchungen werden nur für den allgemeinen, d. h prak-
tisch interessanten Fall durchgeführt (analog Teil I, Pkt. 3.).
Es werden mathematisch-statistische Eigenschaften zweier Vari-
anten der Folgen-Erzeugung untersucht.
Mit der Verwendung von Ergebnissen aus Teil I werden i. d.
auch die entsprechenden Bezeichnungen übernommen. Weitere
grundlegende Bezeichnungen sind:
(X
untersucht werden.
Die Untersuchungen werden nur für den allgemeinen, d. h prak-
tisch interessanten Fall durchgeführt (analog Teil I, Pkt. 3.).
Es werden mathematisch-statistische Eigenschaften zweier Vari-
anten der Folgen-Erzeugung untersucht.
Mit der Verwendung von Ergebnissen aus Teil I werden i. d.
auch die entsprechenden Bezeichnungen übernommen. Weitere
grundlegende Bezeichnungen sind:
(X - Menge aller Anordnungen von k aus n Elementen
P', P
- Menge aller Anordnungen von k aus n Elementen
P', P wird nach der
Variante 1 durch mehrfache Anwendung des APV auf eine fest
vorgegebene Ausgangspermutation X
wird nach der
Variante 1 durch mehrfache Anwendung des APV auf eine fest
vorgegebene Ausgangspermutation X Offensichtlich ist
Offensichtlich ist  D. h. das Verhältnis größter Erwartungswert zu kleinstem bleibt
so wie im Falle einer einmaligen Anwendung des APV (m = 1).
Zur Einschätzung der Variante 1 auf der Basis von (2.1.) und
(2.2.) können somit unmittelbar die numerischen Werte aus
Teil I, Pkt. 3.3. oder 3.4. genutzt werden.
2.2. Folgen von Anordnungen
Die Folge von Anordnungen
D. h. das Verhältnis größter Erwartungswert zu kleinstem bleibt
so wie im Falle einer einmaligen Anwendung des APV (m = 1).
Zur Einschätzung der Variante 1 auf der Basis von (2.1.) und
(2.2.) können somit unmittelbar die numerischen Werte aus
Teil I, Pkt. 3.3. oder 3.4. genutzt werden.
2.2. Folgen von Anordnungen
Die Folge von Anordnungen  wird nach der Variante I
durch mehrfache Anwendung des APV auf eine fest vorgegebene
Ausgangspermutation X
wird nach der Variante I
durch mehrfache Anwendung des APV auf eine fest vorgegebene
Ausgangspermutation X
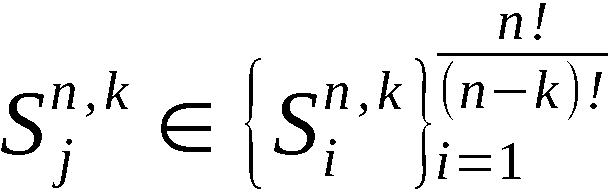 folgende Beziehungen herleiten:
folgende Beziehungen herleiten:


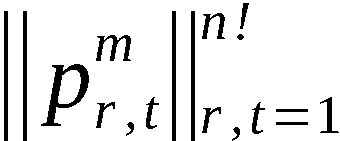 mit
mit  läßt sich im vorliegenden Fall einer homogenen
Markow'schen Kette /6, S.215/, /7, S.393/ als Potenz von P
berechnen:
läßt sich im vorliegenden Fall einer homogenen
Markow'schen Kette /6, S.215/, /7, S.393/ als Potenz von P
berechnen:
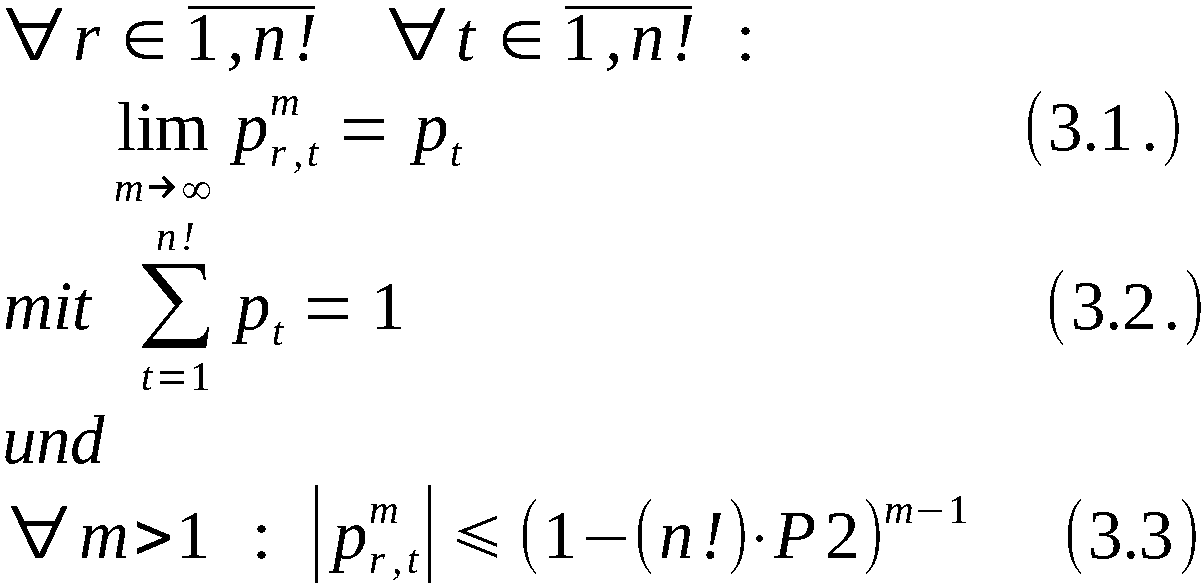

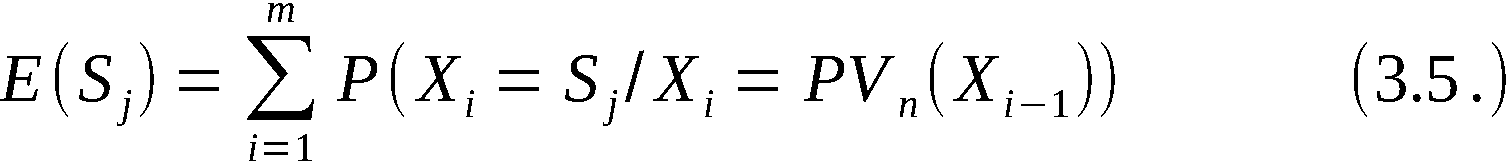
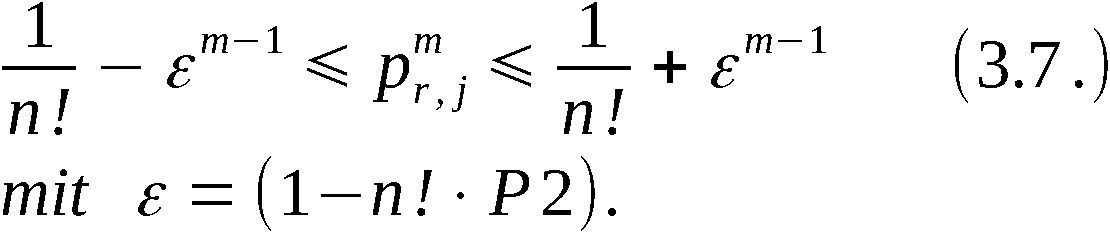
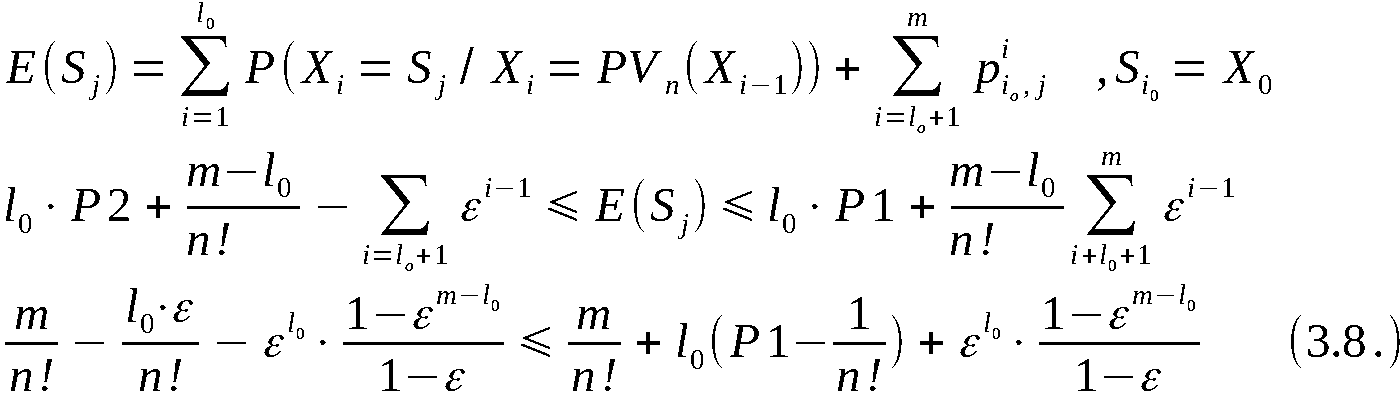
 dient.
D. h.
dient.
D. h. 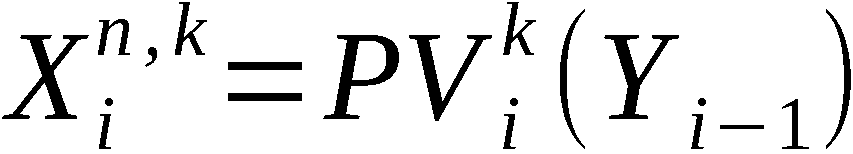 und gleichzeitig wird durch die k Vertauschungen
in Y
und gleichzeitig wird durch die k Vertauschungen
in Y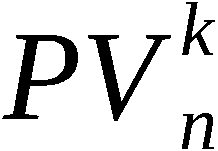 )
eine EP Y
)
eine EP Y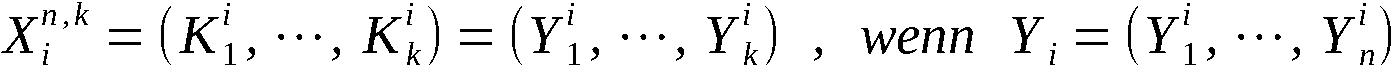
 .
Wie im Pkt. 3.1. soll der Prozeß der Folgenerzeugung als homo-
gene Markow'sche Kette mit der Übergangsmatrix
P(k) = ‖p
.
Wie im Pkt. 3.1. soll der Prozeß der Folgenerzeugung als homo-
gene Markow'sche Kette mit der Übergangsmatrix
P(k) = ‖p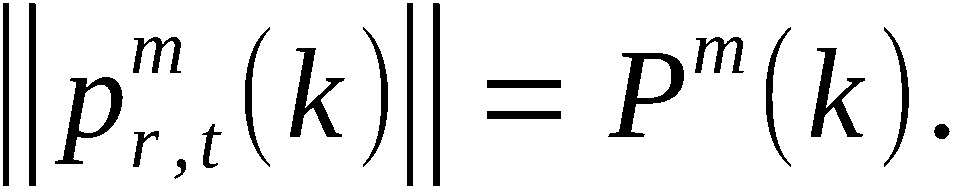
 EP möglich sind) gibt es offensichtlich
(r,t) ∈ (
EP möglich sind) gibt es offensichtlich
(r,t) ∈ (

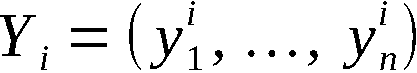 ist nach der Variante 2
der Folgenerzeugung für jede AP S
ist nach der Variante 2
der Folgenerzeugung für jede AP S

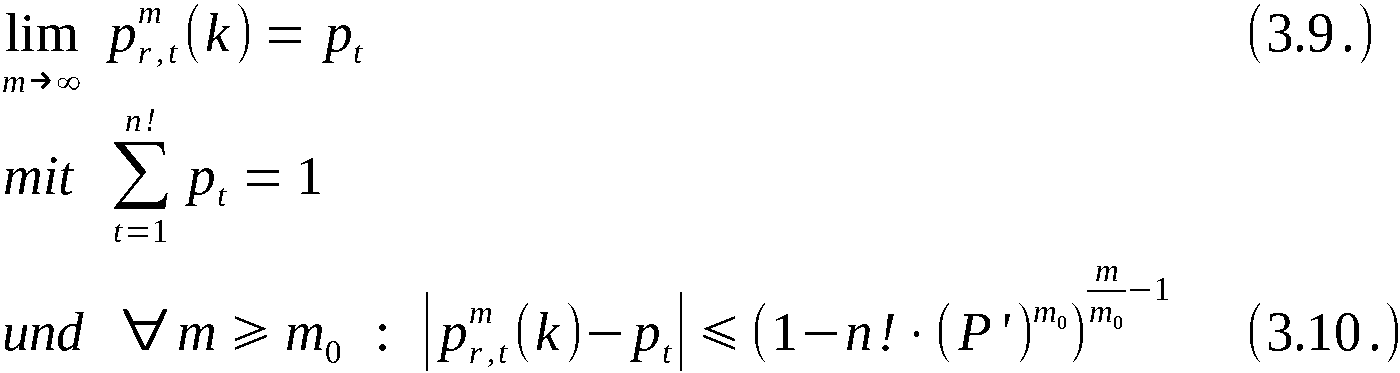

 genau (n-k)! intern erzeugte Permutationen entsprechen, sind
auch die Anordnungen bei beliebiger AP asymptomatisch gleich-
verteilt, d. h.
genau (n-k)! intern erzeugte Permutationen entsprechen, sind
auch die Anordnungen bei beliebiger AP asymptomatisch gleich-
verteilt, d. h.
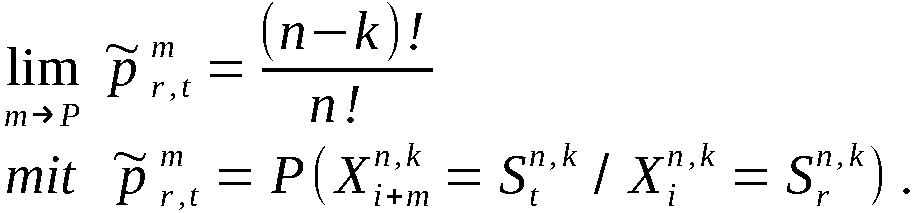

 (p1 entspr. Bl. 45)
(p1 entspr. Bl. 45)